当前位置： 首页 > news >正文

什么是AJAX？

news 2026/1/31 5:07:24

AJAX是一种基于Web的技术，它允许Web应用程序在不刷新整个页面的情况下与服务器进行交互。通过AJAX，Web应用程序可以使用JavaScript向服务器发送异步请求并在不干扰用户的情况下更新页面的部分内容。

AJAX是Asynchronous JavaScript and XML的缩写。尽管名字中包含XML，但实际上AJAX可以使用任何格式的数据进行通信。AJAX最初的实现依赖于XMLHttpRequest对象，但现在可以使用许多不同的技术来实现AJAX。

AJAX的优点之一是减少了Web应用程序与服务器之间的通信量。每次用户与Web应用程序进行交互时，AJAX只需要更新页面的部分内容，而不需要重新加载整个页面。这不仅可以提高Web应用程序的响应速度，而且可以减少Web服务器的负载。

另一个优点是AJAX允许Web应用程序在后台执行任务。例如，Web应用程序可以使用AJAX定期从服务器获取新数据，并将其显示在页面上，而不会中断用户的操作。这使得Web应用程序更加灵活和交互性。

AJAX的一个重要应用是在Web应用程序中实现自动完成。当用户在文本框中输入文本时，Web应用程序可以使用AJAX向服务器发送异步请求，并在下拉列表中显示与输入文本匹配的建议。这种技术可以大大简化用户的输入，并提高用户的满意度。

AJAX的缺点之一是它的实现可能会增加Web应用程序的复杂性。由于AJAX需要使用JavaScript等多个技术，开发人员需要具备多种技能才能有效地实现AJAX。此外，由于AJAX使用JavaScript来更新页面的内容，搜索引擎可能无法正确地索引页面的内容。

总的来说，AJAX是一种非常有用的Web技术，可以提高Web应用程序的响应速度和交互性。然而，开发人员需要仔细考虑其实现方式和对搜索引擎的影响。

怎么学AJAX？

2023最新AJAX入门到实战重磅上线！还在纠结从JS到VUE之间应该学习什么？

一套搞定AJAX，Node，Webpack，Git等前端必备知识点；助力小伙伴快速完成前端框架前置学习！

https://www.bilibili.com/video/BV1MN411y7pw/?spm_id_from=333.999.0.0&vd_source=a9602decec8fcc27bc697e3fe6b51845icon-default.png?t=N4P3https://www.bilibili.com/video/BV1MN411y7pw/?spm_id_from=333.999.0.0&vd_source=a9602decec8fcc27bc697e3fe6b51845本课程从 AJAX 技术入门，掌握前后端数据交互技术，做黑马头条数据管理平台等案例巩固语法和思路，接着学习 Node.js 和 Webpack 以及 npm 模块化等语法，体验前端工程化为后续学习框架做铺垫。最后学习 Git 版本控制系统来管理代码不同版本，以支撑后面 Vue 等框架学习。

相关文章：

什么是AJAX？

AJAX是一种基于Web的技术，它允许Web应用程序在不刷新整个页面的情况下与服务器进行交互。通过AJAX，Web应用程序可以使用JavaScript向服务器发送异步请求并在不干扰用户的情况下更新页面的部分内容。 AJAX是Asynchronous JavaScript and XML的缩写。尽管…...

编程日记 2023/6/10 19:35:59

报表生成器FastReport .Net用户指南：显示数据列、HTML标签

FastReport .Net是一款全功能的Windows Forms、ASP.NET和MVC报表分析解决方案，使用FastReport .NET可以创建独立于应用程序的.NET报表，同时FastReport .Net支持中文、英语等14种语言，可以让你的产品保证真正的国际性。 FastReport.NET官方版…...

编程日记 2023/6/10 19:30:58

bootstrap-dialog弹框，去掉遮盖层，可移动

1.去掉遮盖层的设置data-backdrop"false" <div class"modal fade" id"modal" aria-modal"true" role"dialog" data-backdrop"false" style"width:50%"><div class"modal-dialog modal-l…...

编程日记 2023/6/10 19:25:57

7. user-Agent破解反爬机制

文章目录 1. 为什么要设置反爬机制2. 服务器如何区分浏览器访问和爬虫访问3. 反爬虫机制4. User-Agent是什么5. 如何查询网页的User-Agent6. user-agent信息解析7. 爬虫程序user-agent和浏览器user-agent的区别8. 代码查看爬虫程序的user-agent9. 在代码中加入请求头信息 1. 为…...

编程日记 2023/6/10 19:20:56

3.Nginx+Tomcat负载均衡和动静分离群集

文章目录 NginxTomcat负载均衡和动静分离群集Nginx作用实验七层反向代理nginx动静分离四层反向代理负载均衡 NginxTomcat负载均衡和动静分离群集 Nginx是-款非常优秀的HTTP服务器软件 支持高达50 000个并发连接数的响应拥有强大的静态资源处理能力运行稳定内存、CPU等系统资源…...

编程日记 2023/6/10 19:15:55

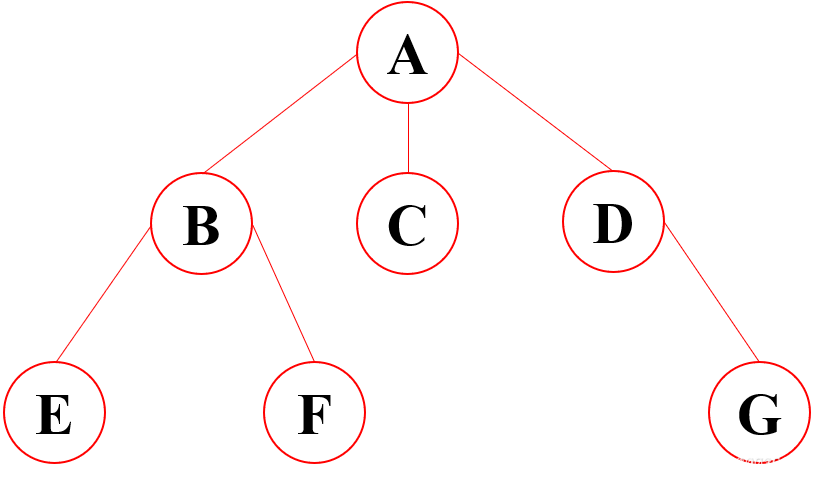
数据结构与算法之树结构

目录 为什么要使用树结构树结构基本概念树的种类树的存储与表示常见的一些树的应用场景为什么要使用树结构 线性结构中不论是数组还是链表，他们都存在着诟病；比如查找某个数必须从头开始查，消耗较多的时间。使用树结构，在插入和查找的性能上相对都会比线性结构要好 树结构…...

编程日记 2023/6/10 19:10:54

【python】 用来将对象持久化的 pickle 模块

pickle 模块可以对一个 Python 对象的二进制进行序列化和反序列化。说白了&#xff0c;就是它能够实现任意对象与二进制直接的相互转化&#xff0c;也可以实现对象与文本之间的相互转化。 比如&#xff0c;我程序里有一个 python 对象&#xff0c;我想把它存到磁盘里&#xff…...

编程日记 2023/6/10 19:05:53

【博客654】prometheus配置抓取保护以防止压力过载

prometheus抓取保护配置以防止压力过载 场景 担心您的应用程序指标可能突然激增&#xff0c;以及指标突然激增导致prometheus压力过载 就像生活中的许多事情一样&#xff0c;标签要有节制。当带有用户 ID 或电子邮件地址的标签被添加到指标时&#xff0c;虽然它不太可能结束…...

编程日记 2023/6/10 19:00:52

Backtrader官方中文文档:第十三章Observers观察者

本文档参考backtrader官方文档，是官方文档的完整中文翻译，可作为backtrader中文教程、backtrader中文参考手册、backtrader中文开发手册、backtrader入门资料使用。 本章包含 backtrader 官方Observers章节全部内容，入口 ： https://backtrader.com/docu/observers-and-sta…...

编程日记 2023/6/10 18:55:48

算法leetcode｜54. 螺旋矩阵（rust重拳出击）

文章目录 54. 螺旋矩阵&#xff1a;样例 1&#xff1a;样例 2&#xff1a;提示&#xff1a; 分析&#xff1a;题解&#xff1a;rust&#xff1a;go&#xff1a;c&#xff1a;python&#xff1a;java&#xff1a;每次循环移动一步&#xff1a;每次循环完成一个顺时针&#xff1a…...

编程日记 2023/6/10 18:50:47

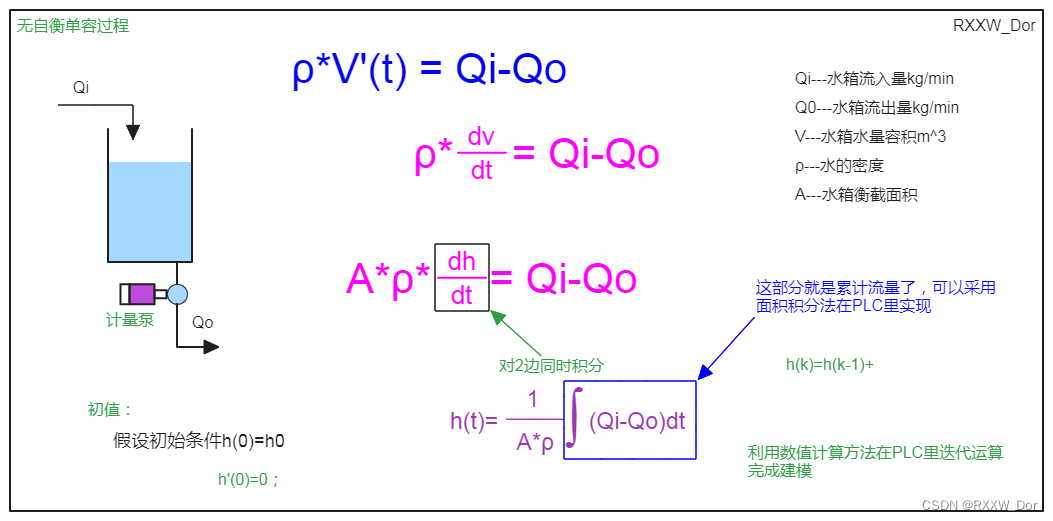
单容水箱建模(自衡单容水箱+无自衡单容水箱)

自衡单容水箱Simulink建模和PLC源代码请参看下面文章链接： 单容双容水箱建模(simulink仿真+PLC代码)_RXXW_Dor的博客-CSDN博客PLC通过伯努利方程近似计算水箱流量详细内容请参看下面的文章博客PLC通过伯努利方程近似计算水箱流量(FC)_怎么用伯努利方程求某水位流量_RXXW_Dor的…...

编程日记 2023/6/10 18:45:46

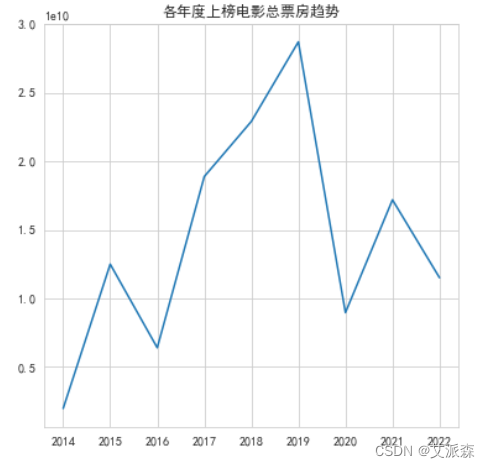
分享Python7个爬虫小案例（附源码）

本次的7个python爬虫小案例涉及到了re正则、xpath、beautiful soup、selenium等知识点&#xff0c;非常适合刚入门python爬虫的小伙伴参考学习。注&#xff1a;若涉及到版权或隐私问题&#xff0c;请及时联系我删除即可。 1.使用正则表达式和文件操作爬取并保存“某吧”某帖子…...

编程日记 2023/6/10 18:40:45

我用ChatGPT写2023高考语文作文（一）：全国甲卷

2023年 全国甲卷 适用地区&#xff1a;广西、贵州、四川、西藏 人们因技术发展得以更好地掌控时间&#xff0c;但也有人因此成了时间的仆人。 这句话引发了你怎样的联想与思考&#xff1f;请写一篇文章。 要求&#xff1a;选准角度&#xff0c;确定立意&#xff0c;明确文体&am…...

编程日记 2023/6/10 18:35:43

c++ modbusTCP

//Modbus TCP是一种基于TCP/IP协议的Modbus协议&#xff0c;它允许Modbus协议通过以太网进行通信。 //在C中&#xff0c;可以使用第三方库来实现Modbus TCP通信&#xff0c;例如libmodbus和QModbus。 //使用libmodbus库实现Modbus TCP通信的示例代码如下&#xff1a; //c #incl…...

编程日记 2023/6/10 18:30:42

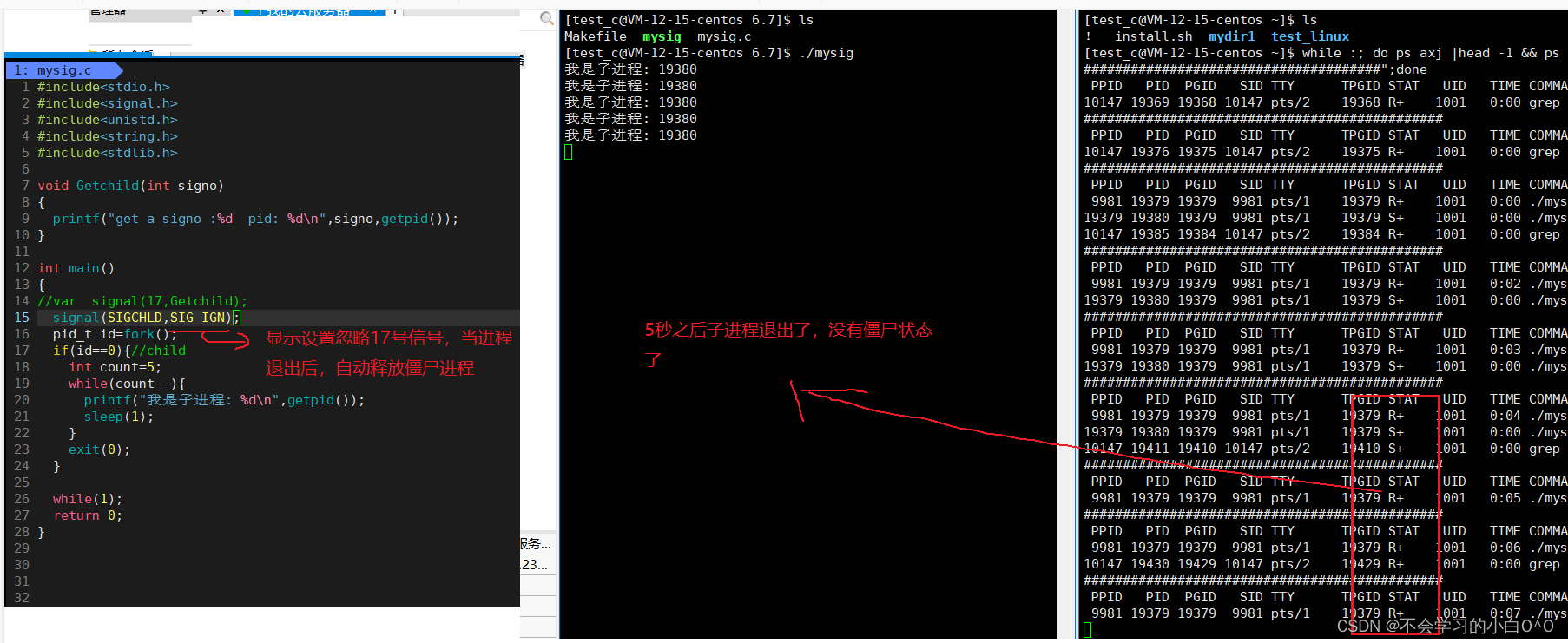
linux(信号结尾)

目录&#xff1a; 1.可重入函数 2.volatile关键字 3.SIGCHLD信号 -------------------------------------------------------------------------------------------------------------------------------- 1.可重入函数----------用来描述一个函数的特点的 1.在单进程当中也存…...

编程日记 2023/6/10 18:25:41

【漏洞修复】node-exporter被检测出来pprof调试信息泄露漏洞

node-exporter被检测出来pprof调试信息泄露漏洞 说在前面解决方法结语 说在前面 惯例开篇吐槽&#xff0c;有些二五仔习惯搞点自研的安全扫描工具&#xff0c;然后加点DIY元素&#xff0c;他也不管扫的准不准&#xff0c;就要给你报个高中危的漏洞&#xff0c;然后就要去修复&…...

编程日记 2023/6/10 18:20:40

在linux 上安装 NFS服务器软件

在 Ubuntu Linux 中创建 NFS 文件系统通常需要完成以下步骤： 安装 NFS 服务器软件。您可以在终端上使用以下命令来安装所需的软件包。sudo apt-get update sudo apt-get install nfs-kernel-server创建要共享的目录。例如，您可以创建一个名为 /var/nfs/shared 的目录。sudo m…...

编程日记 2023/6/10 18:15:38

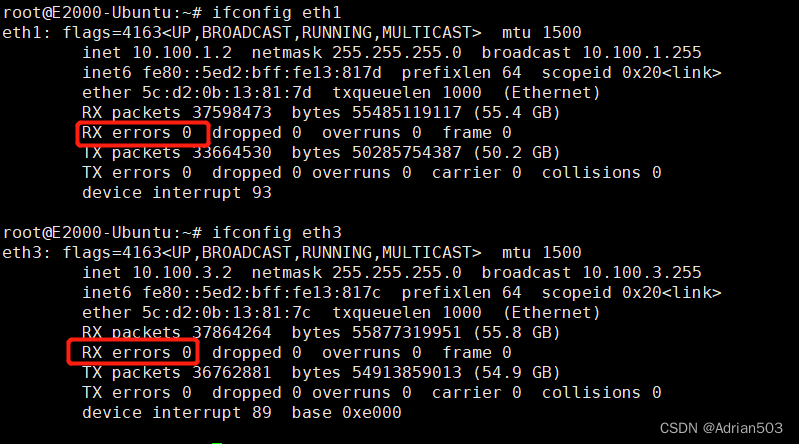
网卡中的Ring buffer -- 解决 rx_resource_errors 丢包

1、软硬件环境 硬件&#xff1a; 飞腾E2000Q 平台 软件&#xff1a; linux 4.19.246 2、问题现象 网卡在高速收包的过程中&#xff0c;出现 rx error , 细查是 rx_resource_errors 如下&#xff1a; rootE2000-Ubuntu:~# ifconfig eth1 eth1: flags4163<UP,BROADCAST,RU…...

编程日记 2023/6/10 18:10:37

六月九号补题日记：Codeforces Round 877 (Div. 2)

专注是不够的&#xff0c;很重要的一方面在于细节&#xff0c;关注细节&#xff1a;精细和专注才是成功的重点&#xff01;&#xff01;&#xff01; A 题意&#xff1a;给你一堆数字&#xff0c;说这一堆数字是由最初的两个数字相减得到的&#xff0c;让你求出两个数字其中一…...

编程日记 2023/6/10 18:05:36

python基础选择题，高中适用

1. 下面哪个是 Python 的注释符号&#xff1f; A. // B. # C. /* D. ; 答案&#xff1a;B 2. 下面哪个是 Python 的赋值运算符&#xff1f; A. B. C. ! D. > 答案&#xff1a;A 3. 下面哪个是 Python 的逻辑运算符&#xff1f; A. && B. || C. ! D. & 答…...

编程日记 2023/6/10 18:00:35

c++ 面试题(1)-----深度优先搜索（DFS）实现

操作系统&#xff1a;ubuntu22.04 IDE:Visual Studio Code 编程语言&#xff1a;C11 题目描述 地上有一个 m 行 n 列的方格&#xff0c;从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子&#xff0c;但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

编程新知 2026/1/10 10:16:16

ffmpeg（四）：滤镜命令

FFmpeg 的滤镜命令是用于音视频处理中的强大工具&#xff0c;可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下&#xff1a; ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜&#xff1a; ffmpeg…...

编程新知 2025/11/9 11:32:13

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台

🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型（LLM）的广泛应用，开发者常面临多个挑战： 各大模型（OpenAI、Claude、Gemini、Ollama）接口风格不统一；缺乏一个统一平台进行模型调用与测试；本地模型 Ollama 的集成与前…...

编程新知 2026/1/25 3:31:07

云原生玩法三问：构建自定义开发环境

云原生玩法三问&#xff1a;构建自定义开发环境 引言 临时运维一个古董项目&#xff0c;无文档&#xff0c;无环境&#xff0c;无交接人&#xff0c;俗称三无。 运行设备的环境老&#xff0c;本地环境版本高&#xff0c;ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

编程新知 2026/1/22 9:24:47

【C++进阶篇】智能指针

C内存管理终极指南&#xff1a;智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

编程新知 2026/1/27 0:19:52

Unity UGUI Button事件流程

场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

编程新知 2026/1/26 2:29:50

在 Spring Boot 中使用 JSP

jsp&#xff1f; 好多年没用了。重新整一下 还费了点时间&#xff0c;记录一下。 项目结构&#xff1a; pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

编程新知 2026/1/27 4:48:06

在树莓派上添加音频输入设备的几种方法

在树莓派上添加音频输入设备可以通过以下步骤完成&#xff0c;具体方法取决于设备类型&#xff08;如USB麦克风、3.5mm接口麦克风或HDMI音频输入&#xff09;。以下是详细指南&#xff1a; 1. 连接音频输入设备 USB麦克风/声卡&#xff1a;直接插入树莓派的USB接口。3.5mm麦克…...

编程新知 2025/11/22 14:54:34

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG

TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码&#xff1a;HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...

编程新知 2026/1/20 7:42:59

C# winform教程(二)----checkbox

一、作用 提供一个用户选择或者不选的状态&#xff0c;这是一个可以多选的控件。 二、属性 其实功能大差不差&#xff0c;除了特殊的几个外&#xff0c;与button基本相同&#xff0c;所有说几个独有的 checkbox属性 名称内容含义appearance控件外观可以变成按钮形状checkali…...

编程新知 2026/1/26 17:05:57