【日常】矩阵正态分布参数检验问题
最近给凯爹做的一个苦力活,统计检验这个东西说实话也挺有趣,跟算法设计一样,好的检验真的是挺难设计的,就有近似算法的那种感觉,检验很难保证size和power都很理想,所以就要做tradeoff,感觉这个假设检验的思路还是挺有趣,所以破例记录一下。
今天阳历生日(其实我每年都是过农历生日),凯爹职场情场皆得意,前脚拿到offer,后脚抱得美人归,说到底凯爹还是个挺励志的人,二战时吃那么多苦,如今终于是苦尽甘来(这不狠宰他一手哈哈哈哈哈哈哈哈
文章目录
- 假设检验① H0:A,BH_0:A,BH0:A,B是对角阵
- 1 生成模拟数据XXX
- 2 虽然生成模拟数据时已知A,BA,BA,B,但假设A,BA,BA,B未知,对其进行估计。
- 2.1 第一种估计方法:Naive
- 2.2 第二种估计方法:Sample
- 2.3 第三种估计方法:Banded(只可对代表时间维度的矩阵BBB使用)
- 3 对A,BA,BA,B的估计值进行假设检验
- 4 上述1-3步骤,每组参数设置{p,q,n,z}\{p,q,n,z\}{p,q,n,z}(共8种组合)重复1000次
- 4.1 对于每组参数设置,计算1000次试验后假设检验①的size
- 4.2 对于每组参数设置,计算1000次试验后假设检验①的power
- Appendix 代码实现
- 假设检验② H0:RA1=RA2H_0:R_A^1=R_A^2H0:RA1=RA2
- 5 生成模拟数据XXX
- 6 估计B~(g)\tilde B^{(g)}B~(g)的3种方法
- 6.1 第一种估计方法:Naive
- 6.2 第二种估计方法:Sample
- 6.3 第三种估计方法:Banded
- 7 对两个协相关矩阵AAA的相关系数矩阵RA(g)R^{(g)}_ARA(g)进行假设检验
- 8 上述5-7步骤,每组参数设置{p,q,n,z}\{p,q,n,z\}{p,q,n,z}(共8种组合),重复1000次
- 代码实现
假设检验① H0:A,BH_0:A,BH0:A,B是对角阵
1 生成模拟数据XXX
对于matrix normal distribution,MNpq(0,A,B)MN_{pq}(0,A,B)MNpq(0,A,B),000代表零均值,A,BA,BA,B分别是行与列的协方差。从分布中抽取两组模拟数据,X(1)=(X1(1),...,Xn1(1)),X(2)=(X1(2),...,Xn2(2))X^{(1)}=(X_1^{(1)},...,X_{n1}^{(1)}),X^{(2)}=(X_1^{(2)},...,X_{n2}^{(2)})X(1)=(X1(1),...,Xn1(1)),X(2)=(X1(2),...,Xn2(2)),X1(1)X_1^{(1)}X1(1)维度为p×qp\times qp×q。两组数据的分布中AAA不一样,BBB一样,n1=n2=nn_1=n_2=nn1=n2=n
参数设置:p={10,20},q={10,20},n={5,8}p=\{10,20\},q=\{10,20\},n=\{5,8\}p={10,20},q={10,20},n={5,8}
矩阵Ap×p=A_{p\times p}=Ap×p=
{H0:IH1:I+U+δI1+δ\left\{\begin{aligned} &H_0:I\\ &H_1:\frac{I+U+\delta I}{1+\delta} \end{aligned}\right. ⎩⎨⎧H0:IH1:1+δI+U+δI
矩阵Bq×q:bij=0.4∣i−j∣,1≤i,j≤qB_{q\times q}:b_{ij}=0.4^{|i-j|},1\le i,j\le qBq×q:bij=0.4∣i−j∣,1≤i,j≤q
其中δ=∣λmin(I+U)∣+0.05\delta=|\lambda_{\min}(I+U)|+0.05δ=∣λmin(I+U)∣+0.05,λmin(I+U)\lambda_{\min}(I+U)λmin(I+U)表示取矩阵I+UI+UI+U的最小特征根的绝对值。UUU是稀疏对称矩阵,有z={2}z=\{2\}z={2}个非零元素。有z2\frac z22z个非零元素在下/上三角中(不在对角线上),服从U(2(logpnq)1/2,4(logpnq)1/2)U(2\left(\frac{\log p}{nq}\right)^{1/2},4\left(\frac{\log p}{nq}\right)^{1/2})U(2(nqlogp)1/2,4(nqlogp)1/2)均匀分布,正负随机,位置随机。
2 虽然生成模拟数据时已知A,BA,BA,B,但假设A,BA,BA,B未知,对其进行估计。
对于每种估计方法,需要重复第3部分。
2.1 第一种估计方法:Naive
直接代入真实的A,BA,BA,B
2.2 第二种估计方法:Sample
Ap×pA_{p\times p}Ap×p的朴素估计:A~∝1nq∑k=1nXkXk⊤\tilde A\propto \frac{1}{nq}\sum_{k=1}^nX_kX_k^\topA~∝nq1∑k=1nXkXk⊤,Bq×qB_{q\times q}Bq×q的朴素估计:B~∝1np∑k=1nXk⊤Xk\tilde B\propto \frac{1}{np}\sum_{k=1}^nX_k^\top X_kB~∝np1∑k=1nXk⊤Xk,注意,此处估计值差了常数倍,不可直接调用。
当AAA已知时(用A~\tilde AA~代替),可以改进BBB的估计:
B^=1np∑k=1nXk⊤(A~c)−1Xk\widehat B=\frac1{np}\sum_{k=1}^nX_k^\top\left(\frac{\tilde A}{c}\right)^{-1}X_k B=np1k=1∑nXk⊤(cA~)−1Xk
ccc是一个未知常数,后续计算中会被抵消。
当BBB已知时(用B~\tilde BB~代替),可以改进AAA的估计:
A^=1nq∑k=1nXk(A~c)−1Xk⊤\widehat A=\frac1{nq}\sum_{k=1}^nX_k\left(\frac{\tilde A}{c}\right)^{-1}X_k^\top A=nq1k=1∑nXk(cA~)−1Xk⊤
ccc是一个未知常数,后续计算中会被抵消。
2.3 第三种估计方法:Banded(只可对代表时间维度的矩阵BBB使用)
只保留B^\widehat BB对角线以及两侧副对角线上的值:
Bˉ={b^i,jif ∣i−j∣≤20otherwise\bar B=\left\{\begin{aligned}&\hat b_{i,j}&&\text{if }|i-j|\le 2\\ &0&&\text{otherwise} \end{aligned}\right. Bˉ={b^i,j0if ∣i−j∣≤2otherwise
3 对A,BA,BA,B的估计值进行假设检验
3.1 假设检验① H0:BH_0:BH0:B是对角阵
记Mn=max1≤i<j≤qMij,MijM_n=\max_{1\le i<j\le q}M_{ij},M_{ij}Mn=max1≤i<j≤qMij,Mij为bijb_{ij}bij标准化后的值,Mij=b^ij2θ^ij/(np)M_{ij}=\frac{\hat b_{ij}^2}{\hat \theta_{ij}/(np)}Mij=θ^ij/(np)b^ij2,此处常数ccc会相互抵消,其中:
θ^ij=1np∑k=1n∑l=1p[(Xk⊤(A~c)−1/2)i,l(Xk⊤(A~c)−1/2)j,l−b^i,j]2\hat \theta_{ij}=\frac1{np}\sum_{k=1}^n\sum_{l=1}^p\left[\left(X_k^\top\left(\frac{\tilde A}{c}\right)^{-1/2}\right)_{i,l}\left(X_k^\top\left(\frac{\tilde A}{c}\right)^{-1/2}\right)_{j,l}-\hat b_{i,j}\right]^2 θ^ij=np1k=1∑nl=1∑pXk⊤(cA~)−1/2i,lXk⊤(cA~)−1/2j,l−b^i,j2
由于Mn−4logp+loglogpM_n-4\log p+\log\log pMn−4logp+loglogp服从Gumble分布,设统计量Φα=I(Mn≥α+4logq−loglogq)\Phi_\alpha=I(M_n\geq_{\alpha}+4\log q-\log\log q)Φα=I(Mn≥α+4logq−loglogq),其中qα=−log(8π)−2loglog(1−α)−1q_\alpha=-\log(8\pi)-2\log\log(1-\alpha)^{-1}qα=−log(8π)−2loglog(1−α)−1
当Φα=1\Phi_\alpha=1Φα=1时拒绝BBB是对角阵的原假设。
3.2 类似地,假设检验① H0:AH_0:AH0:A是对角阵
相当于转置X(1)X^{(1)}X(1),再重复3.1操作,即,对应ppp换成qqq,Xk⊤X_k^\topXk⊤换成XkX_kXk,A~\tilde AA~换成B~\tilde BB~
3.3 检验协方差AAA哪些位置不为0
Ψ(A)={(i,j):ai,j≠0,1≤i<j≤p}Ψ(τ=4)={(i,j):Mi,j≥τp,1≤i<j≤p}\Psi(A)=\{(i,j):a_{i,j}\neq 0,1\le i<j\le p\}\\ \Psi(\tau=4)=\{(i,j):M_{i,j}\ge\tau p,1\le i<j\le p\} Ψ(A)={(i,j):ai,j=0,1≤i<j≤p}Ψ(τ=4)={(i,j):Mi,j≥τp,1≤i<j≤p}
3.4 检验协方差BBB哪些位置不为0
Ψ(B)={(i,j):bi,j≠0,1≤i<j≤q}Ψ(τ=4)={(i,j):Mi,j≥τq,1≤i<j≤q}\Psi(B)=\{(i,j):b_{i,j}\neq 0,1\le i<j\le q\}\\ \Psi(\tau=4)=\{(i,j):M_{i,j}\ge\tau q,1\le i<j\le q\} Ψ(B)={(i,j):bi,j=0,1≤i<j≤q}Ψ(τ=4)={(i,j):Mi,j≥τq,1≤i<j≤q}
4 上述1-3步骤,每组参数设置{p,q,n,z}\{p,q,n,z\}{p,q,n,z}(共8种组合)重复1000次
参数设置:p={10,20},q={10,20},n1=n2=n={5,8},z={2},α=5%p=\{10,20\},q=\{10,20\},n_1=n_2=n=\{5,8\},z=\{2\},\alpha=5\%p={10,20},q={10,20},n1=n2=n={5,8},z={2},α=5%,需要满足np≥q,nq≥pnp\ge q,nq\ge pnp≥q,nq≥p
论文参数设置:p={50,200},q={50,200},n1=n2=n={10,50},z={8},α=5%p=\{50,200\},q=\{50,200\},n_1=n_2=n=\{10,50\},z=\{8\},\alpha=5\%p={50,200},q={50,200},n1=n2=n={10,50},z={8},α=5%
4.1 对于每组参数设置,计算1000次试验后假设检验①的size
Size=P(原假设为真,拒绝原假设)=P(犯第一类错误),即假设检验①种矩阵A0A_0A0被拒绝的概率,好的方法需要将size控制在0.05以内。
4.2 对于每组参数设置,计算1000次试验后假设检验①的power
Power=P(原假设为假,拒绝原假设),即假设检验①种A1,BA_1,BA1,B被拒绝的概率。
Appendix 代码实现
这个仿真实现并不难,当然最好是用matlab写,这里给出numpy的示例代码。
-
矩阵正态分布随机变量的生成可以用scipy.stats里封装好的方法,也可以用cholesky分解来做。
-
测试结果表明小规模数据上的size还行,但是power明显不太好,但是原论文的效果就很漂亮:
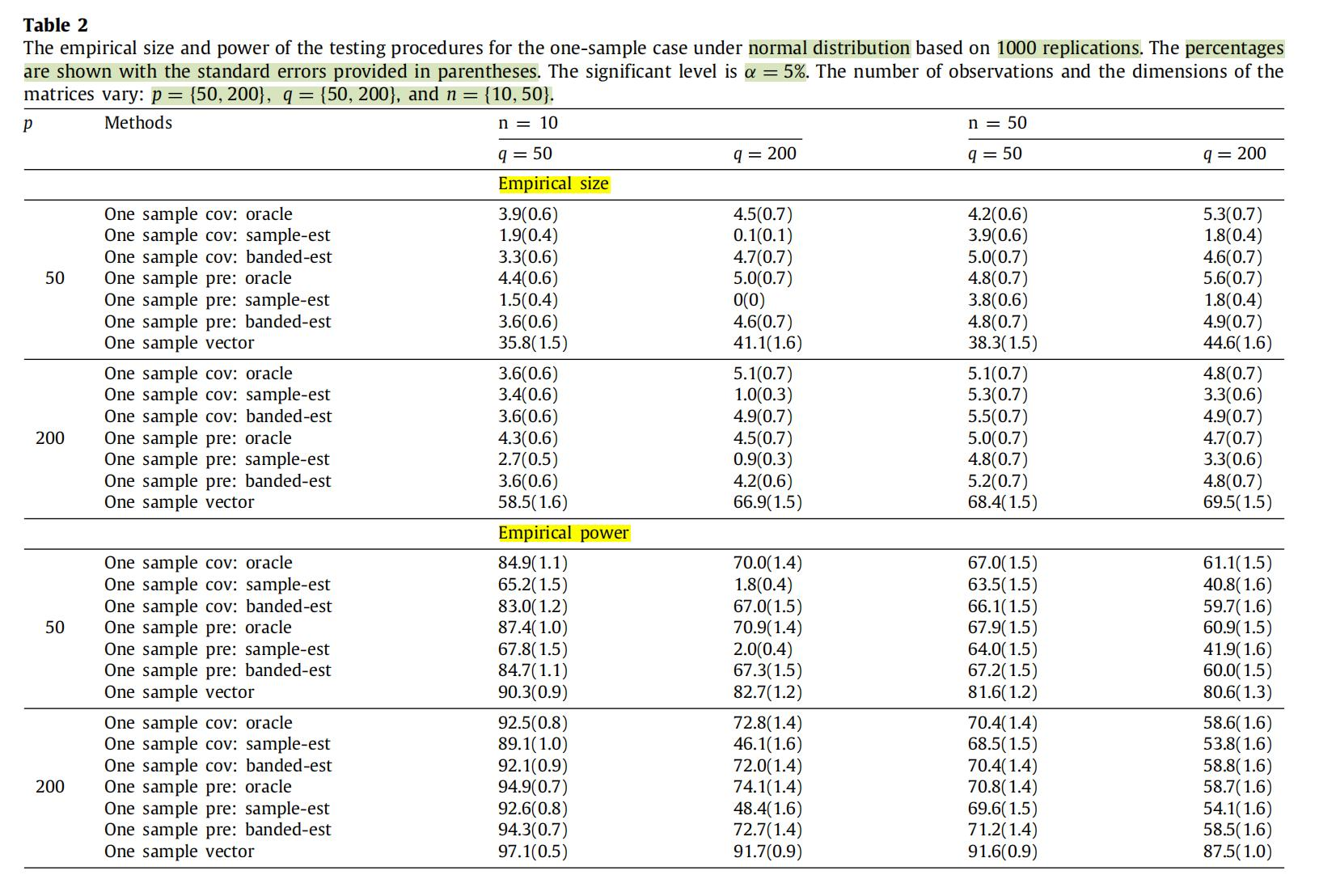
- 但是这个量级的参数跑起来会特别慢。
# -*- coding: UTF-8 -*-
# @author: caoyang
# @email: caoyang@163.sufe.edu.cnimport math
import time
import numpy as np
from scipy.linalg import sqrtm
from scipy import stats# Randomly generate matrix normal distributed matrix.
# M is a p-by-q matrix, U is a p-by-p matrix, and V is a q-by-q matrix.
def randomize_matrix_normal_variable(M, U, V):# X_rand = np.random.randn(*M.shape)# P = np.linalg.cholesky(U)# Q = np.linalg.cholesky(V)# return M + P @ X_rand @ Q.Treturn stats.matrix_normal(M, U, V).rvs()# Randomly generate matrix U
def randomize_matrix_u(p, q, n, z=2):temp = np.sqrt((np.log(p) / n / q))low = 2 * temphigh = 4 * tempU = np.zeros((p, p)) # initializetotal_index = [(i, j) for i in range(p) for j in range(p)]np.random.shuffle(total_index)upper_index = []lower_index = []i = 0while len(upper_index) < int(z / 2) and len(lower_index) < int(z / 2):if total_index[i][0] < total_index[i][1] and len(upper_index) < int(z / 2):upper_index.append((total_index[i][0], total_index[i][1]))lower_index.append((total_index[i][1], total_index[i][0]))elif total_index[i][0] > total_index[i][1] and len(lower_index) < int(z / 2):lower_index.append((total_index[i][0], total_index[i][1]))upper_index.append((total_index[i][1], total_index[i][0]))i += 1for upper_indice, lower_indice in zip(upper_index, lower_index):sign = 2 * np.random.randint(0, 2) - 1 # random 1 and -1 for signvalue = sign * np.random.uniform(low, high)U[upper_indice] = valueU[lower_indice] = valuereturn U# Randomly generate matrix A
def randomize_matrix_a(hypothesis, p, q, n, z=2):if hypothesis == 0:return np.eye(p)elif hypothesis == 1:U = randomize_matrix_u(p, q, n, z)delta = abs(np.min(np.linalg.eigvals(np.eye(p) + U))) + .05return (np.eye(p) + U + delta * np.eye(p)) / (1 + delta)assert False, f'Hypothesis should be 0 or 1 but got {hypothesis} !'# Randomly generate matrix B
def randomize_matrix_b(q):# return np.eye(q)return np.array([[0.4 ** (abs(i - j)) for j in range(q)] for i in range(q)])# Calculate tilde A and tilde B
def calc_tilde_A_and_B(p, q, n, sample):tilde_A = np.zeros((p, p))for X in sample:tilde_A += X @ X.Ttilde_A /= (n * q)tilde_B = np.zeros((q, q))for X in sample:tilde_B += X.T @ Xtilde_B /= (n * p)return tilde_A, tilde_B# Method 1
def estimate_method_1(A, B):hat_A = Ahat_B = Breturn hat_A, hat_B# Method 2
def estimate_method_2(p, q, n, sample):tilde_A, tilde_B = calc_tilde_A_and_B(p, q, n, sample)hat_A = np.zeros((p, p))for X in sample:hat_A += X @ np.linalg.inv(tilde_B) @ X.That_A /= (n * q)hat_B = np.zeros((q, q))for X in sample:hat_B += X.T @ np.linalg.inv(tilde_A) @ Xhat_B /= (n * q)return hat_A, hat_B# Method 3
def estimate_method_3(p, q, n, sample):hat_A, hat_B = estimate_method_2(p, q, n, sample)for i in range(p):for j in range(p):if abs(i - j) > 2:hat_B[i, j] = 0return hat_A, hat_B# Hypothesis 1: B is diagonal matrix
def test_B(p, q, n, sample, tilde_A, hat_B, alpha=.05, tau=4):hat_theta = np.zeros((q, q))tilde_A_inv = sqrtm(np.linalg.inv(tilde_A))for i in range(q):for j in range(q):res = 0for k in range(n):X_k_tilde_A_inv = sample[k].T @ tilde_A_invfor l in range(p):res += (X_k_tilde_A_inv[i, l] * X_k_tilde_A_inv[j, l] - hat_B[i, j]) ** 2hat_theta[i, j] = reshat_theta /= (n * p)M = n * p * hat_B * hat_B / (hat_theta)for i in range(q):for j in range(i + 1):M[i, i] = -999M_n = np.max(M)q_alpha = -np.log(8 * math.pi) - 2 * np.log(-np.log(1 - alpha))Phi_alpha = 1 * (M_n > q_alpha + 4 * np.log(q) - np.log(np.log(q)))return Phi_alpha, M# Hypothesis 2: A is diagonal matrix
def test_A(p, q, n, sample, tilde_B, hat_A, alpha=.05, tau=4):sample = list(map(lambda X: X.T, sample))return test_B(q, p, n, sample, tilde_B, hat_A, alpha)def run():p_choices = [10, 20]q_choices = [10, 20]n_choices = [5, 8]# p_choices = [50, 200]# q_choices = [50, 200]# n_choices = [10, 50]N = 1000alpha = .05z = 2tau = 4time_string = time.strftime('%Y%m%d%H%M%S')filename = f'res1-{time_string}.txt'with open(filename, 'w') as f:passfor p in p_choices:for q in q_choices:for n in n_choices:print(f'p = {p}, q = {q}, n = {n}')count_Phi_alpha_B_0 = 0count_Phi_alpha_A_0 = 0count_Phi_alpha_B_1 = 0count_Phi_alpha_A_1 = 0for _ in range(N):A_0 = randomize_matrix_a(0, p, q, n, z)A_1 = randomize_matrix_a(1, p, q, n, z)B = randomize_matrix_b(q)sample_0 = [randomize_matrix_normal_variable(np.zeros((p, q)), A_0, B) for _ in range(n)]sample_1 = [randomize_matrix_normal_variable(np.zeros((p, q)), A_1, B) for _ in range(n)]tilde_A_0, tilde_B_0 = calc_tilde_A_and_B(p, q, n, sample_0)tilde_A_1, tilde_B_1 = calc_tilde_A_and_B(p, q, n, sample_0)hat_A_0, hat_B_0 = estimate_method_2(p, q, n, sample_0)hat_A_1, hat_B_1 = estimate_method_2(p, q, n, sample_1)# hat_A_0, hat_B_0 = estimate_method_1(A_0, B)# hat_A_1, hat_B_1 = estimate_method_1(A_1, B)Phi_alpha_B_0, M_B0 = test_B(p, q, n, sample_0, tilde_A_0, hat_B_0, alpha, tau)Phi_alpha_A_0, M_A0 = test_A(p, q, n, sample_0, tilde_B_0, hat_A_0, alpha, tau)Phi_alpha_B_1, M_B1 = test_B(p, q, n, sample_1, tilde_A_1, hat_B_1, alpha, tau)Phi_alpha_A_1, M_A1 = test_A(p, q, n, sample_1, tilde_B_1, hat_A_1, alpha, tau)count_Phi_alpha_B_0 += Phi_alpha_B_0count_Phi_alpha_A_0 += Phi_alpha_A_0count_Phi_alpha_B_1 += Phi_alpha_B_1count_Phi_alpha_A_1 += Phi_alpha_A_1###################################### 3.3 & 3.4Psi_B0 = (B != 0) * 1 # 得到零一矩阵(可用于画热力图)Psi_tau_B0 = (M_B0 >= tau * p) * 1 # 得到零一矩阵(可用于画热力图)where_B0 = np.where(Psi_B0 == 1)print([(x, y) for (x, y) in zip(where_B0[0], where_B0[1])]) # 得到零一矩阵中元素1的坐标where_tau_B0 = np.where(Psi_tau_B0 == 1)print([(x, y) for (x, y) in zip(where_tau_B0[0], where_tau_B0[1])]) # 得到零一矩阵中元素1的坐标# ----------------------------------Psi_A0 = (A_0 != 0) * 1 # 得到零一矩阵(可用于画热力图)Psi_tau_A0 = (M_A0 >= tau * q) * 1 # 得到零一矩阵(可用于画热力图)where_A0 = np.where(Psi_A0 == 1)print([(x, y) for (x, y) in zip(where_A0[0], where_A0[1])]) # 得到零一矩阵中元素1的坐标where_tau_A0 = np.where(Psi_tau_A0 == 1)print([(x, y) for (x, y) in zip(where_tau_A0[0], where_tau_A0[1])]) # 得到零一矩阵中元素1的坐标# ----------------------------------# 以下类似Psi_B1 = (B != 0) * 1Psi_tau_B1 = (M_B1 >= tau * p) * 1# ----------------------------------Psi_A1 = (A_1 != 0) * 1Psi_tau_A1 = (M_A1 >= tau * q) * 1#####################################print('Phi_alpha_B_0: ', count_Phi_alpha_B_0)print('Phi_alpha_A_0: ', count_Phi_alpha_A_0)print('Phi_alpha_B_1: ', count_Phi_alpha_B_1)print('Phi_alpha_A_1: ', count_Phi_alpha_A_1)with open(filename, 'a') as f:f.write(f'Phi_alpha_B_0: {count_Phi_alpha_B_0}\n')f.write(f'Phi_alpha_A_0: {count_Phi_alpha_A_0}\n') f.write(f'Phi_alpha_B_1: {count_Phi_alpha_B_1}\n') f.write(f'Phi_alpha_A_1: {count_Phi_alpha_A_1}\n')
run()
假设检验② H0:RA1=RA2H_0:R_A^1=R_A^2H0:RA1=RA2
5 生成模拟数据XXX
数据从matrix normal distribution,MNpq(0,A(g),B(g))MN_{pq}(0,A^{(g)},B^{(g)})MNpq(0,A(g),B(g))中生成。B(g)B^{(g)}B(g)为AR(1)AR(1)AR(1)过程的自相关系数矩阵,系数为0.8和0.9.此处简化使用协方差矩阵Bq×qg:bij=0.4∣i−j∣,1≤i,j≤qB^{g}_{q\times q}:b_{ij}=0.4^{|i-j|},1\le i,j\le qBq×qg:bij=0.4∣i−j∣,1≤i,j≤q的相关系数矩阵,同**1 生成模拟数据XXX**中一样。
H0H_0H0下,A(1)=A(2)=Σ(1)=D1/2Σ∗(1)D1/2A^{(1)}=A^{(2)}=\Sigma^{(1)}=D^{1/2}{\Sigma^*}^{(1)}D^{1/2}A(1)=A(2)=Σ(1)=D1/2Σ∗(1)D1/2,其中:
Σ∗(1)=(σi,j∗(1))={1if i=j0.5if 5(k−1)+1≤i≠j≤5kwith k=1,...,p/50otherwise{\Sigma^*}^{(1)}=(\sigma_{i,j}^{*(1)})=\left\{\begin{aligned} &1&&\text{if }i=j\\ &0.5&&\text{if }5(k-1)+1\le i\neq j\le 5k\text{ with }k=1,...,p/5\\ &0&&\text{otherwise} \end{aligned}\right. Σ∗(1)=(σi,j∗(1))=⎩⎨⎧10.50if i=jif 5(k−1)+1≤i=j≤5k with k=1,...,p/5otherwise
即非零值集中在对角线附近,DDD为对焦矩阵,di,i=Unif(0.5,2.5)d_{i,i}=Unif(0.5,2.5)di,i=Unif(0.5,2.5)
H1H_1H1下,(A(1))−1=(Σ(1)+δI)/(1+δ)(A^{(1)})^{-1}=(\Sigma^{(1)}+\delta I)/(1+\delta)(A(1))−1=(Σ(1)+δI)/(1+δ),(A(2))−1=(Σ(1)+U+δI)/(1+δ)(A^{(2)})^{-1}=(\Sigma^{(1)}+U+\delta I)/(1+\delta)(A(2))−1=(Σ(1)+U+δI)/(1+δ),两者相差一个稀疏矩阵UUU,其中δ=∣min{λmin(Σ(1)),λmin(Σ(1)+U)}∣+0.05\delta=|\min\{\lambda_{\min}(\Sigma^{(1)}),\lambda_{\min}(\Sigma^{(1)}+U)\}|+0.05δ=∣min{λmin(Σ(1)),λmin(Σ(1)+U)}∣+0.05。UUU是稀疏对称矩阵,有z=2z=2z=2个非零元素,有z/2z/2z/2个非零元素在下/上三角中(不在对角线上),服从U(3(logpnq)1/2,5(logpnq)1/2)U(3\left(\frac{\log p}{nq}\right)^{1/2},5\left(\frac{\log p}{nq}\right)^{1/2})U(3(nqlogp)1/2,5(nqlogp)1/2)的均匀分布,正负随机,位置随机。
6 估计B~(g)\tilde B^{(g)}B~(g)的3种方法
对于每种估计方法,需要重复第7部分
6.1 第一种估计方法:Naive
直接代入真实的B(g)B^{(g)}B(g)
6.2 第二种估计方法:Sample
B~(g)=1ngp∑k=1ng(Xk(g))⊤Xk(g)\tilde B^{(g)}=\frac{1}{n_gp}\sum_{k=1}^{n_g}(X_k^{(g)})^\top X_k^{(g)} B~(g)=ngp1k=1∑ng(Xk(g))⊤Xk(g)
6.3 第三种估计方法:Banded
只保留B~(g)\tilde B^{(g)}B~(g)对角线以及两侧副对角线上的值:
Bˉ(g)={b~i,j(g)if ∣i−j∣≤20otherwise\bar B^{(g)}=\left\{\begin{aligned}&\tilde b_{i,j}^{(g)}&&\text{if }|i-j|\le 2\\&0&&\text{otherwise}\end{aligned}\right. Bˉ(g)={b~i,j(g)0if ∣i−j∣≤2otherwise
7 对两个协相关矩阵AAA的相关系数矩阵RA(g)R^{(g)}_ARA(g)进行假设检验
7.1 假设检验② H0:RA1=RA2H_0:R_A^1=R_A^2H0:RA1=RA2,即第一组和第二组的相关系数矩阵是否相同
公式太长,直接截图了:

7.2 检验相关系数矩阵RA1R_A^1RA1和RA2R_A^2RA2哪些位置不同
Ψ∗(RA1,RA2)={(i,j):r^i,j(1)≠r^i,j(2),1≤i<j≤p}Ψ∗(τ=4)={(i,j):Mi,j∗≥τlog(p),1≤i<j≤p}\Psi^*(R_A^1,R_A^2)=\{(i,j):\hat r_{i,j}^{(1)}\neq \hat r_{i,j}^{(2)},1\le i<j\le p\}\\ \Psi^*(\tau=4)=\{(i,j):M_{i,j}^*\ge \tau \log (p),1\le i < j \le p\} Ψ∗(RA1,RA2)={(i,j):r^i,j(1)=r^i,j(2),1≤i<j≤p}Ψ∗(τ=4)={(i,j):Mi,j∗≥τlog(p),1≤i<j≤p}
8 上述5-7步骤,每组参数设置{p,q,n,z}\{p,q,n,z\}{p,q,n,z}(共8种组合),重复1000次

代码实现
跟第一个检验的代码有很大的共通处,其实我看到第二个才知道这个检验在做什么事情,大概是自相关时间序列上的协方差和相关系数检验:
# -*- coding: UTF-8 -*-
# @author: caoyang
# @email: caoyang@163.sufe.edu.cnimport math
import time
import numpy as np
from scipy.linalg import sqrtm
from scipy import stats# Randomly generate matrix normal distributed matrix.
# M is a p-by-q matrix, U is a p-by-p matrix, and V is a q-by-q matrix.
def randomize_matrix_normal_variable(M, U, V):return stats.matrix_normal(M, U, V).rvs()# Randomly generate matrix U
def randomize_matrix_u(p, q, n, z=2):temp = np.sqrt((np.log(p) / n / q))low = 3 * temphigh = 5 * tempU = np.zeros((p, p)) # initializetotal_index = [(i, j) for i in range(p) for j in range(p)]np.random.shuffle(total_index)upper_index = []lower_index = []i = 0while len(upper_index) < int(z / 2) and len(lower_index) < int(z / 2):if total_index[i][0] < total_index[i][1] and len(upper_index) < int(z / 2):upper_index.append((total_index[i][0], total_index[i][1]))lower_index.append((total_index[i][1], total_index[i][0]))elif total_index[i][0] > total_index[i][1] and len(lower_index) < int(z / 2):lower_index.append((total_index[i][0], total_index[i][1]))upper_index.append((total_index[i][1], total_index[i][0]))i += 1for upper_indice, lower_indice in zip(upper_index, lower_index):sign = 2 * np.random.randint(0, 2) - 1 # random 1 and -1 for signvalue = sign * np.random.uniform(low, high)U[upper_indice] = valueU[lower_indice] = valuereturn U# Randomly generate matrix A
def randomize_matrix_a(hypothesis, p, q, n, z=2):Sigma_star = np.zeros((p, p))def _check(_i, _j):if _i == _j:return Falsefor _k in range(p // 5):if 5 * (_k - 1) <= _i < 5 * _k and 5 * (_k - 1) <= _j < 5 * _k:return Truereturn Falsefor i in range(p):for j in range(p):if i == j:Sigma_star[i, j] = 1elif _check(i, j):Sigma_star[i, j] = .5else:Sigma_star[i, j] = 0D = np.diag(np.random.uniform(.5, 2.5, p))D_sqrt = np.sqrt(D)Sigma = D_sqrt @ Sigma_star @ D_sqrt if hypothesis == 0:A_1 = Sigma[:, :]A_2 = Sigma[:, :]return A_1, A_2elif hypothesis == 1:U = randomize_matrix_u(p, q, n, z)delta = abs(min(np.min(np.linalg.eigvals(Sigma + U)),np.min(np.linalg.eigvals(Sigma)),)) + .05A_1 = np.linalg.inv((Sigma + delta * np.eye(p)) / (1 + delta))A_2 = np.linalg.inv((Sigma + U + delta * np.eye(p)) / (1 + delta))# A_1 = (Sigma + delta * np.eye(p)) / (1 + delta)# A_2 = (Sigma + U + delta * np.eye(p)) / (1 + delta)return A_1, A_2assert False, f'Hypothesis should be 0 or 1 but got {hypothesis} !'# Randomly generate matrix B
def randomize_matrix_b(q):# return np.eye(q)return np.array([[0.4 ** (abs(i - j)) for j in range(q)] for i in range(q)])# Calculate tilde B
def calc_tilde_B(p, q, n, sample):tilde_B = np.zeros((q, q))for X in sample:tilde_B += X.T @ Xtilde_B /= (n * p)return tilde_B# Calculate hat A
def calc_hat_A(p, q, n, sample, tilde_B):hat_A = np.zeros((p, p))tilde_B_inv = np.linalg.inv(tilde_B)for X in sample:hat_A += X @ tilde_B_inv @ X.That_A /= (n * q)return hat_A# Calculate hat R
def calc_hat_R(p, q, n, hat_A):hat_R = np.zeros((p, p))for i in range(p):for j in range(p):hat_R[i, j] = hat_A[i, j] / np.sqrt(hat_A[i, i] * hat_A[j, j])return hat_R# Method 1
def estimate_method_1(B):hat_B = Breturn hat_B# Method 2
def estimate_method_2(p, q, n, sample):tilde_B = calc_tilde_B(p, q, n, sample)return tilde_B# Method 3
def estimate_method_3(p, q, n, sample):bar_B = calc_tilde_B(p, q, n, sample)for i in range(p):for j in range(p):if abs(i - j) > 2:bar_B[i, j] = 0return bar_B# Hypothesis: R_A^1 = R_A^2
def test(p, q, n, A_1, A_2, B, sample_1, sample_2, alpha=0.05, tau=4):tilde_B_1 = calc_tilde_B(p, q, n, sample_1)tilde_B_2 = calc_tilde_B(p, q, n, sample_2)# 上面是用的estimate_method_2, 可以用另外两种# tilde_B_1 = estimate_method_1(B)# tilde_B_2 = estimate_method_1(B)# tilde_B_1 = estimate_method_2(p, q, n, sample_1)# tilde_B_2 = estimate_method_2(p, q, n, sample_2)# tilde_B_1 = estimate_method_3(p, q, n, sample_1)# tilde_B_2 = estimate_method_3(p, q, n, sample_2)hat_A_1 = calc_hat_A(p, q, n, sample_1, tilde_B_1)hat_A_2 = calc_hat_A(p, q, n, sample_2, tilde_B_2)hat_R_1 = calc_hat_R(p, q, n, hat_A_1)hat_R_2 = calc_hat_R(p, q, n, hat_A_2)tilde_B_1_inv = sqrtm(np.linalg.inv(tilde_B_1))tilde_B_2_inv = sqrtm(np.linalg.inv(tilde_B_2))M = np.zeros((p, p))for i in range(p):for j in range(p):theta_1 = 0theta_2 = 0for k in range(n):X_k_tilde_B_1_inv = sample_1[k] @ tilde_B_1_invX_k_tilde_B_2_inv = sample_2[k] @ tilde_B_2_invfor l in range(q):theta_1 += (X_k_tilde_B_1_inv[i, l] * X_k_tilde_B_1_inv[j, l] - hat_A_1[i, j]) ** 2theta_2 += (X_k_tilde_B_2_inv[i, l] * X_k_tilde_B_2_inv[j, l] - hat_A_2[i, j]) ** 2theta_1 /= (n * q)theta_2 /= (n * q)pretty_theta_1 = theta_1 / hat_A_1[i, i] / hat_A_1[j, j]pretty_theta_2 = theta_2 / hat_A_2[i, i] / hat_A_2[j, j]M[i, j] = ((hat_R_1[i, j] - hat_R_2[i, j]) ** 2) / (pretty_theta_1 / n / q + pretty_theta_2 / n / q)for i in range(p):for j in range(i + 1):M[i, i] = -999M_n = np.max(M)q_alpha = -np.log(8 * math.pi) - 2 * np.log(-np.log(1 - alpha))Phi_alpha = 1 * (M_n > q_alpha + 4 * np.log(q) - np.log(np.log(q)))########################### 7.2# ------------------------Psi_star = 1 * (hat_R_1 != hat_R_2) # 得到零一矩阵(可用于画热力图)hat_Psi_star = 1 * (M > tau * np.log(p)) # 得到零一矩阵(可用于画热力图)where_Psi_star = np.where(Psi_star == 1) # print([(x, y) for (x, y) in zip(where_Psi_star[0], where_Psi_star[1])]) # 得到零一矩阵中元素1的坐标where_hat_Psi_star = np.where(hat_Psi_star == 1)# print([(x, y) for (x, y) in zip(where_hat_Psi_star[0], where_hat_Psi_star[1])]) # 得到零一矩阵中元素1的坐标##########################return Phi_alpha, Psi_star, hat_Psi_stardef run():p_choices = [10, 20]q_choices = [10, 20]n_choices = [5, 8]z = 2alpha = .05N = 1000tau = 4time_string = time.strftime('%Y%m%d%H%M%S')filename = f'res2-{time_string}.txt'with open(filename, 'w') as f:passfor p in p_choices:for q in q_choices:for n in n_choices:print(f'p = {p}, q = {q}, n = {n}')count_Phi_alpha_0 = 0count_Phi_alpha_1 = 0for _ in range(N):A_01, A_02 = randomize_matrix_a(0, p, q, n, z)A_11, A_12 = randomize_matrix_a(1, p, q, n, z)B = randomize_matrix_b(q)sample_01 = [randomize_matrix_normal_variable(np.zeros((p, q)), A_01, B) for _ in range(n)]sample_02 = [randomize_matrix_normal_variable(np.zeros((p, q)), A_02, B) for _ in range(n)]sample_11 = [randomize_matrix_normal_variable(np.zeros((p, q)), A_11, B) for _ in range(n)]sample_12 = [randomize_matrix_normal_variable(np.zeros((p, q)), A_12, B) for _ in range(n)]# 7.2的Psi在这里返回Phi_alpha_0, Psi_star_0, hat_Psi_star_0 = test(p, q, n, A_01, A_02, B, sample_01, sample_02, alpha, tau)Phi_alpha_1, Psi_star_1, hat_Psi_star_1 = test(p, q, n, A_11, A_12, B, sample_11, sample_12, alpha, tau)count_Phi_alpha_0 += Phi_alpha_0count_Phi_alpha_1 += Phi_alpha_1print('Phi_alpha_0: ', count_Phi_alpha_0)print('Phi_alpha_1: ', count_Phi_alpha_1)with open(filename, 'a') as f:f.write(f'Phi_alpha_0: {count_Phi_alpha_0}\n')f.write(f'Phi_alpha_1: {count_Phi_alpha_1}\n')if __name__ == '__main__':run()
相关文章:

【日常】矩阵正态分布参数检验问题
最近给凯爹做的一个苦力活,统计检验这个东西说实话也挺有趣,跟算法设计一样,好的检验真的是挺难设计的,就有近似算法的那种感觉,检验很难保证size和power都很理想,所以就要做tradeoff,感觉这个假…...

QML矩形(Rectangle)
Rectangle 用于绘制矩形 常见的属性: 填充颜色:纯色:color 渐变 :Gradient类 渐变的优先级大于纯色Gradient(渐变色): 渐变由多种颜色定义,这些颜色将无缝混合,…...

CSS自定义鼠标样式
CSS自定义鼠标样式 属性值 属性描述url需使用的自定义光标的 URLdefault默认光标(通常是一个箭头)auto默认。浏览器设置的光标crosshair光标呈现为十字线pointer光标呈现为指示链接的指针(一只手)move此光标指示某对象可被移动e…...
春招Leetcode刷题日记-D4-双指针算法-滑动窗口快慢指针
D4-双指针算法-滑动窗口&&快慢指针快慢指针算力扣141. 环形链表思路代码力扣142. 环形链表 II思路代码滑动窗口力扣76. 最小覆盖子串思路代码力扣424. 替换后的最长重复字符思路代码快慢指针算 快慢指针算法,多用于链表当中,常见的如࿱…...
【go】结合一个go开源项目分析谷歌浏览器cookie为什么不安全 附go项目导包失败怎么解决教程
本文创作背景 源于谷歌浏览器提示密码被泄露 并且某站很快收到了异地企图登录的提醒。 当即怀疑是不是谷歌浏览器保存的密码不安全,最后查阅诸多资料 并找到一个go语言编写的开源项目进行研究,虽然最终不能确定密码是如何泄露的 但研究结论还是让人不由感…...

Windows瘦身方法
一、快速删除系统盘临时文件方法, 1、winr打开运行对话框,输入%temp%命令,如图1 图1 2、打开temp文件夹,如图2,选择所有文件,鼠标右键删除或按Del键删除。 图2 二、磁盘清理 1、winr,输入cleanmgr&#x…...
19. 删除链表的倒数第 N 个结点
题目链接:https://leetcode.cn/problems/remove-nth-node-from-end-of-list/进阶:你能尝试使用一趟扫描实现吗?解题思路:最简单的方法是先遍历一次链表,得到链表的长度len,然后再一次遍历链表,遍…...
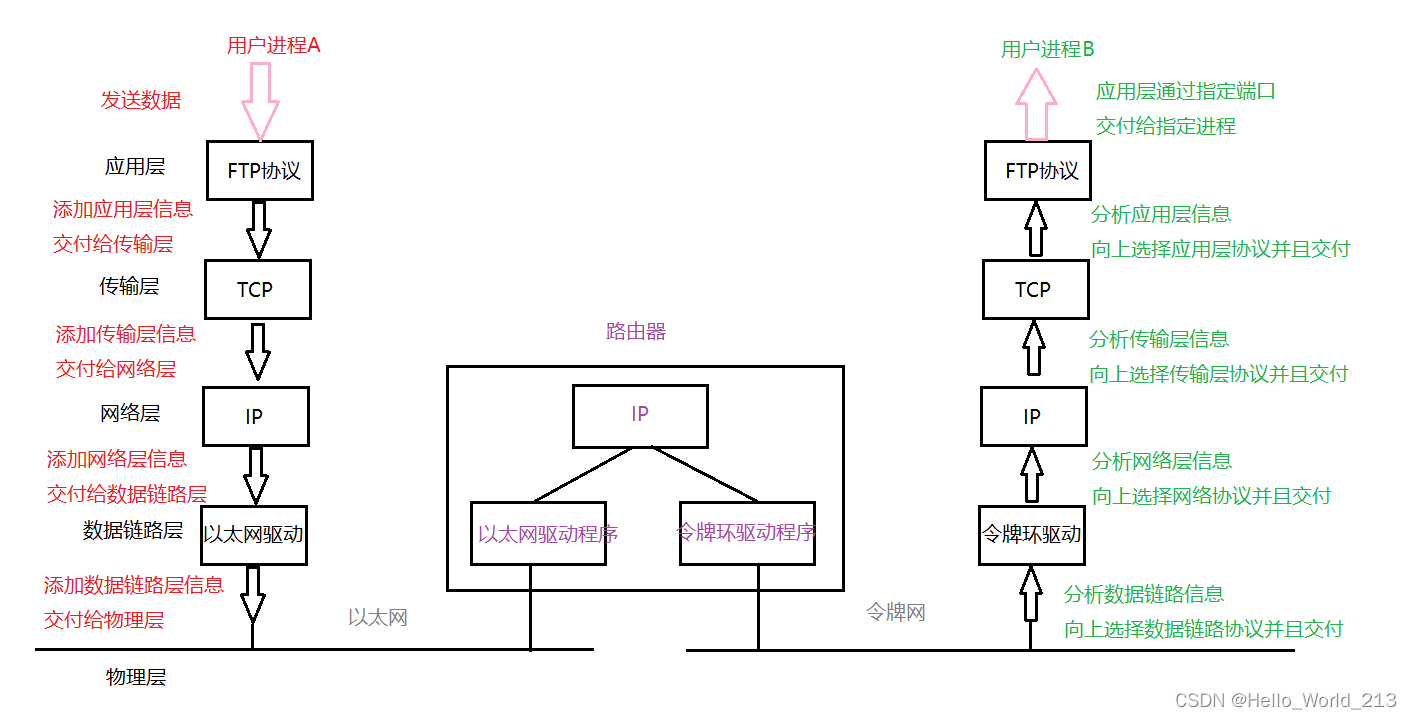
【Linux】网络编程 - 基础概念
目录 一.OSI七层模型vsTCP/IP五层模型 1.一些周边概念 2.OSI七层模型 3.TCP/IP五层模型 4.网络传输流程图 二.什么是MAC地址 三.什么是IP/IP地址 1.什么是IP 2.什么是IP地址 四.什么是端口号 一.OSI七层模型vsTCP/IP五层模型 1.一些周边概念 局域网vs广域网 网络互…...

Unity 多语言 轻量高效的多语言工具集 LanguageManager
效果展示 支持excel导入自动化 组件化 更方便 也提供直接获取多语言的接口 没有挂 LanguageText的对象也可以获取多语言文本内容 支持 Format接口 可以传递N个参数进来组装多语言 支持首次系统语言自测 支持语言切换后本地自动保存配置 支持实时切换 同步刷新所有UI 容错处…...

在Linux和Windows上安装zookeeper-3.5.9
记录:378场景:在CentOS 7.9操作系统上,安装zookeeper-3.5.9。在Windows上操作系统上,安装zookeeper-3.5.9。版本:JDK 1.8 CentOS 7.9 zookeeper-3.5.9官网地址:https://zookeeper.apache.org/源码地址&…...
【ESP32+freeRTOS学习笔记-(八)资源管理】
目录1、 资源使用概况2、互斥方法之一:基本临界区2.1、taskENTER_CRITICAL_FROM_ISR() 和taskEXIT_CRITICAL_FROM_ISR()3、互斥方法之二:挂起或锁定调度程序3.1 vTaskSuspendAll()3.2 xTaskResumeAll()4 互斥方法三:互斥信号量(和…...
)
P1427 小鱼的数字游戏(赋值运算符和String)
小鱼的数字游戏 题目描述 小鱼最近被要求参加一个数字游戏,要求它把看到的一串数字 aia_iai(长度不一定,以 000 结束),记住了然后反着念出来(表示结束的数字 000 就不要念出来了)。这对小鱼…...

Java学的好,工作不愁找
俗话说的好:“Java学的好,工作不愁找”,不管我们学习哪一门语言,我们都要掌握从抽象化中提取出来的方法,这样你才能提高我们的学习能力,并且在学习新事物的时候可以提取我们自己的想法。学习java࿰…...

表情包可视化编辑、生成配置信息数据工具
合成GIF图片 - 表情包 后续,用于快速、便捷生成 img_config.js 中 要生成的GIF每一帧数据(写入头像图片信息参数); 1、先上传 写入GIF中头像 标准图,同时获取图片信息,更新 写入GIF中头像 初始值࿰…...

java简单循环结构
while循环结构 Java提供的while条件循环。它的基本用法是: while (条件表达式) {循环语句 } // 继续执行后续代码while循环在每次循环开始前,首先判断条件是否成立。如果计算结果为true,就把循环体内的语句执行一遍,如果计算结果…...
【Servlet+Jsp+Mybatis+Maven】WEB图书馆管理系统
web图书馆管理系统一、绪论二、流程和其页面展示效果流程页面效果项目结构三、具体实现第一步:备数据库表第二步:编写登录前端代码第三步:利用过滤器处理安全问题第四步:控制层去实现相关调用第五步:实现持久化层与数据…...
【WPF】WindowChrome 自定义窗口完美实现
WindowChrome 自定义窗口完美实现简介效果图自定义最小化、最大化、关闭按钮布局实现结语简介 Microsoft官网关于 WindowChome 的介绍 截取Microsoft文章的一段话: 若要在保留其标准功能时自定义窗口,可以使用该 WindowChrome 类。 该 WindowChrome…...
Python客户端使用SASL_SSL连接Kafka需要将jks密钥转换为pem密钥,需要转化成p12格式再转换pem才能适配confluent_kafka包
证书生成 生成证书以及jks参考以下文章 https://blog.csdn.net/qq_41527073/article/details/121148600 证书转换jks -> pem 需要转化成p12以下转换才能适配confluent_kafka包,直接jks转pem会报错不能使用,具体参考以下文章 https://www.ngui.cc/z…...

JDK8 ConcurrentHashMap源码分析
文章目录常量说明put() 方法putVal() 方法initTable():初始化数组treeifyBin():链表转红黑树tryPresize():初始化数组扩容TreeBin() 构造方法:生成红黑树putTreeVal():往红黑树中插入值helpTransfer():多线…...

前置知识-初值问题、欧拉法、改进欧拉法
1.1 初值问题 初值问题是科研、工程技术应用中最常见的一类问题, 一阶常微分方程的初值问题表述如下: 已知 u ( x ) u(x) u(x) 的起始点 ( x 0 , u 0 ) \left(x_0, u_0\right)...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...

高防服务器价格高原因分析
高防服务器的价格较高,主要是由于其特殊的防御机制、硬件配置、运营维护等多方面的综合成本。以下从技术、资源和服务三个维度详细解析高防服务器昂贵的原因: 一、硬件与技术投入 大带宽需求 DDoS攻击通过占用大量带宽资源瘫痪目标服务器,因此…...

Java数组Arrays操作全攻略
Arrays类的概述 Java中的Arrays类位于java.util包中,提供了一系列静态方法用于操作数组(如排序、搜索、填充、比较等)。这些方法适用于基本类型数组和对象数组。 常用成员方法及代码示例 排序(sort) 对数组进行升序…...
