【学习笔记】[AGC048D] Pocky Game
这是一个非平等博弈。但是只要求你判断胜负,本身也不是一道结论题,所以可以用 D P DP DP来解决。
结论:第一堆石子剩的越多,先手玩家获胜的概率越大。这直接引出了一个非常感性的结论:每次取石子时要么取一堆,要么只取一个。很难理性证明这个博弈策略是正确的,但是博弈本身就是很玄学的东西,似乎我们找不出来一套普适的理论去判断游戏的胜负。那么只要这个策略本身具有合理性就可以采纳。就这道题而言,取一堆石子可以看成是加快游戏进度,取一个石子可以看成是让游戏的步数延长。看来这道题当中游戏步数是非常重要的维度,我们可以通过比较游戏步数的大小来判定胜负。
然后就是编 D P DP DP状态。设 f l , r f_{l,r} fl,r表示剩 [ l + 1 , r ] [l+1,r] [l+1,r]堆中石子时先手获胜, a l a_l al的最小数目, g l , r g_{l,r} gl,r表示剩 [ l , r − 1 ] [l,r-1] [l,r−1]堆中石子时后手获胜(后手先操作), a r a_r ar的最小数目。注意,这里我们要求 [ l , r ] [l,r] [l,r]中的石子堆都非空。这个状态给我一种 border \text{border} border的感觉,也就是要么左端点被截断或者右端点被截断,正好就是对应左右两端中两堆石子被消耗的过程。
接着编具体的转移。其实并不复杂:如果 g l + 1 , r > a r g_{l+1,r}>a_r gl+1,r>ar那么直接将第 l l l堆取空就行,有 f l , r = 1 f_{l,r}=1 fl,r=1;否则先手一定是消耗,并且 a l > 1 a_l>1 al>1,任意时刻如果 a l < f l , r − 1 a_l<f_{l,r-1} al<fl,r−1那么后手就会将第 r r r堆取完,从而先手必败,那么分类讨论:
1.1 1.1 1.1 如果 g l + 1 , r = 1 g_{l+1,r}=1 gl+1,r=1,那么一定要是后手取完,并且此时 a l a_l al恰好为 f l , r − 1 f_{l,r-1} fl,r−1,有 f l , r = f l , r − 1 + a r f_{l,r}=f_{l,r-1}+a_r fl,r=fl,r−1+ar
1.2 1.2 1.2 如果 g l + 1 , r ≠ 1 g_{l+1,r}\ne 1 gl+1,r=1,那么当 a l = f l , r − 1 a_l=f_{l,r-1} al=fl,r−1时第 r r r堆也恰好为 g l + 1 , r − 1 g_{l+1,r}-1 gl+1,r−1,此时再将 a l a_l al取完就变成先手必胜了,有 f l , r = f l , r − 1 + a r − g l + 1 , r + 1 f_{l,r}=f_{l,r-1}+a_r-g_{l+1,r}+1 fl,r=fl,r−1+ar−gl+1,r+1。
后手和先手是对称的就不说了。这个 D P DP DP转移还挺容易推错的,可能主要是因为没有想到临界时两端的石子数目都不为 0 0 0。
复杂度 O ( n 2 ) O(n^2) O(n2)。
#include<bits/stdc++.h>
#define ll long long
#define fi first
#define se second
#define pb push_back
#define db double
using namespace std;
int T,n;
ll a[105],f[105][105],g[105][105];
int main(){ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);cin>>T;while(T--){cin>>n;for(int i=1;i<=n;i++)cin>>a[i];memset(f,0x3f,sizeof f),memset(g,0x3f,sizeof g);for(int i=1;i<=n;i++){f[i][i]=1,g[i][i]=1;}for(int len=2;len<=n;len++){for(int l=1;l<=n-len+1;l++){int r=l+len-1;if(g[l+1][r]>a[r])f[l][r]=1;else f[l][r]=f[l][r-1]+a[r]-g[l+1][r]+1;if(f[l][r-1]>a[l])g[l][r]=1;else g[l][r]=g[l+1][r]+a[l]-f[l][r-1]+1;}}if(n==1||f[1][n]<=a[1]){cout<<"First"<<"\n";}else{cout<<"Second"<<"\n";}}
}相关文章:

【学习笔记】[AGC048D] Pocky Game
这是一个非平等博弈。但是只要求你判断胜负,本身也不是一道结论题,所以可以用 D P DP DP来解决。 结论:第一堆石子剩的越多,先手玩家获胜的概率越大。这直接引出了一个非常感性的结论:每次取石子时要么取一堆…...
Qgis中进行Shp和Excel属性连接实现百强县公共预算空间分析
前言 在之前的博文中,将2022的全国百强县一般公共预算收入的数据下载到了本地,博客原文地址:一种使用Java的快速将Web中表格转换成Excel的方法。对于不关注时空位置关系的一般分析,到此也就基本够用了。但是,如果站在全…...

ES6 新增的循环方法
在 ES6(ECMAScript 2015)中,新增了一些循环方法,这些方法可以帮助我们更方便地遍历数组、字符串、Set、Map 等数据结构。本文将介绍一些常用的 ES6 循环方法。 for…of 循环 for…of 循环是一种遍历可迭代对象的方法,…...

移动端事件300ms延迟解决
有移动端与PC端的项目开发,那么移动端和PC端开发上是存在差异的,比如 click 事件的300ms 延迟,即移动Web页面上的click事件响应都要慢上300ms,移动设备访问Web页面时往往需要 “双击” 或者 “捏开” 来放大页面看清页面的具体内容…...
NRF52832的DFU
开发环境: Winsodw:10 nRF5_SDK:17.1.0 1 工具安装 1.1 gcc-arm-none-eabi Downloads | GNU Arm Embedded Toolchain Downloads – Arm Developer 下载“gcc-arm-none-eabi-10.3-2021.10-win32.exe”,接提示安装。注意安装完…...
开源WebRTC库放大器模式在采集桌面图像时遇到的DPI缩放与内存泄漏问题排查
目录 1、在非100%的显示比例下放大器采集到的桌面图像不全问题 1.1、通过manifest文件禁止系统对软件进行缩放 1.2、调用SetThreadDpiAwarenessContext函数,禁止系统对目标线程中的窗口进行缩放 1.3、使用winver命令查看Windows的年月版本 2、使用放大器模式遇…...

敲黑板!java反射机制和原理
获取Class对象:首先,你需要获取表示要操作的类的Class对象。可以使用以下三种方式之一来获取Class对象: Class.forName()方法:使用类的全限定名获取Class对象,例如:Class<? Class<?> clazz MyC…...
【大数据工具】HBase 集群搭建与基本使用
HBase 集群搭建 HBase 安装包下载地址:https://archive.apache.org/dist/hbase/ 安装 HBase 的前提: ZooKeeper 集群 OKHadoop 集群 OK 1. HBase 集群安装 1. 将 HBase 软件包上传至 Hadoop0 解压并重命名 使用 FileZilla 将 hbase-1.3.1-bin.tar.g…...
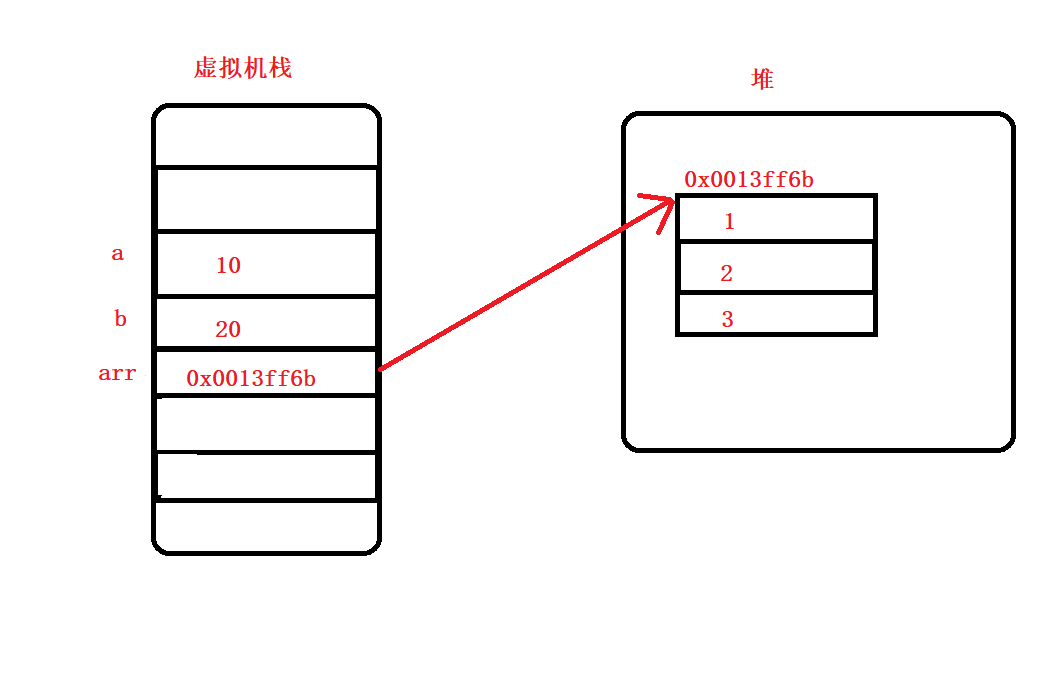
【Java】数组详解
文章目录 一、数组的基本认识1.1 数组的概念1.2数组的创建与初始化1.3 数组的使用 二、数组的类型 — 引用类型2.1 JVM 内存分布2.2 什么是引用类型2.3 基本类型变量与引用类型变量的区别2.4 Java 中的 null 三、数组的应用3.1 保存数据3.2 函数参数3.3 函数返回值 一、数组的基…...
NumPy库的学习
本文主要记录的是笔者在B站自学Numpy库的学习笔记。 引入numpy库 import numpy as np矩阵的创建 创建一个二行三列的矩阵。 array np.array([[1,2,3],[2,3,4]])查看array的行数、形状、元素数量 print("number of dim:",array.ndim) print("shape:"…...

CentOS安装IRIS
最近电脑提搞了,可以无顾虑创建虚拟机了,试一下在Linux安装IRIS,适用CentOS7.6上安装Intersystem公司的IRIS数据库,资料基本是空白,分享一下。 首先安装解压软件unzip和libicu,最小化安装的缺,…...

华为OD机试真题 JavaScript 实现【最多几个直角三角形】【2023Q1 100分】
一、题目描述 有 N 条线段,长度分别为 a[1]-a[n]。 现要求你计算这 N 条线段最多可以组合成几个直角三角形,每条线段只能使用一次,每个三角形包含三条线段。 二、输入描述 第一行输入一个正整数 T (1< T< 100) ,表示有…...

vue3中的reactive、ref、toRef和toRefs
目录 reactivereactive的实现原理使用reactive的注意事项 refref的实现原理使用ref的注意事项 toRef和toRefsref和reactive的使用比较 reactive reactive用于创建响应式对象,它返回一个对象的响应式代理。即:它返回的对象以及其中嵌套的对象都会通过 Pr…...

数字图像处理与Python实现-图像增强经典算法汇总
图像增强经典算法汇总 文章目录 图像增强经典算法汇总1、像素变换2、图像逆变换3、幂律变换4、对数变换5、图像均衡化6、对比度受限自适应直方图均衡(CLAHE)7、对比度拉伸8、Sigmoid校正9、局部对比度归一化10、总结本文将对图像增强经典算法做一个简单的汇总。图像增强的经典…...

tag提示词总结
顺序的权重 越靠前的tag权重越大,越靠后的tag权重越小经验来讲,将图像质量相关的tag放在前面,例如masterpiece,best quality等;接着添加主体画风等;最后添加一些不太重要的细节 权重增减 (tag):…...

微信小程序原生开发功能合集二十:导航栏、tabbar自定义及分包功能介绍
本章实现导航栏及tabbar的自定义处理的相关方法介绍及效果展示。 另外还提供小程序开发基础知识讲解课程,包括小程序开发基础知识、组件封装、常用接口组件使用及常用功能实现等内容,具体如下: 1. CSDN课程: https://edu.csdn.net/course/detail/37977 2. 5…...

高通 Camera HAL3:项目开发技术点总结
做高通 Camera HAL3开发的一些技术点的总结、整理。 做个记录,方便后续查阅。 1.目录、so、配置文件 productName是项目名 out Target路径:\out\target\product\productName\chi-cdk:\vendor\qcom\proprietary\chi-cdk\ldc node࿱…...

chatgpt赋能python:Python怎么删除列表中的最大值和最小值
Python怎么删除列表中的最大值和最小值 在Python中,一个列表(List)是一种非常常见的数据结构,它允许我们以有序的方式存储和访问数据。但是,有时候我们需要从列表中删除最大或最小的值,以满足我们的特定需…...

简述Vue的生命周期以及每个阶段做的事情
03_简述Vue的生命周期以及每个阶段做的事情 思路 给出概念 列举出生命周期各个阶段 阐述整体流程 结合实际 扩展:vue3变化 回答范例 每个vue组件实例被创建后都会经过一系列步骤。比如它需要数据观测、模板编译、挂载实例到dom、以及数据变化的时候更新dom、…...

LeetCode-C#-0004.寻找两个正序数组的中位数
0.声明 该题目来源于LeetCode 如有侵权,立马删除。 解法不唯一,如有新解法可一同讨论。 1.题目 0004寻找两个正序数组的中位数 给定两个大小分别为m和n的正序(从小到大)数组nums1和nums2。 请你找出并返回着两个正序数组的中位…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...
