Lecture 20 Topic Modelling
目录
- Topic Modelling
- A Brief History of Topic Models
- LDA
- Evaluation
- Conclusion
Topic Modelling
-
makeingsense of text
- English Wikipedia: 6M articles
- Twitter: 500M tweets per day
- New York Times: 15M articles
- arXiv: 1M articles
- What can we do if we want to learn something about these document collections?
-
questions
- What are the less popular topics on Wikipedia?
- What are the big trends on Twitter in the past month?
- How do the social issues evolve over time in New York Times from 1900s to 2000s?
- What are some influential research areas?
-
topic models to the rescue
- Topic models learn common, overlapping themes in a document collection
- Unsupervised model
- No labels; input is just the documents!
- What’s the output of a topic model?
- Topics: each topic associated with a list of words
- Topic assignments: each document associated with a list of topics
-
what do topics look like
-
A list of words
-
Collectively describes a concept or subject
-
Words of a topic typically appear in the same set of documents in the corpus(words overlapping in documents)

-
Wikipedia topics(broad)

-
Twitter topics(short,conversational)

-
New York Times topics

-
-
applications of topic models
- Personalised advertising(e.g. types of products bought)
- Search engine
- Discover senses of polysemous words(e.g. apple: fruit, company, two different clusters)
A Brief History of Topic Models
-
latent semantic analysis

-
LSA: truncate

-
issues
- Positive and negative values in the U U U and V T V^T VT
- Difficult to interpret(negative values)

-
-
probabilistic LSA
-
based on a probabilistic model to get rid of negative values

-
issues
- No more negative values!
- PLSA can learn topics and topic assignment for documents in the train corpus
- But it is unable to infer topic distribution on new documents
- PLSA needs to be re-trained for new documents
-
-
latent dirichlet allocation(LDA)
- Introduces a prior to the document-topic and topicword distribution
- Fully generative: trained LDA model can infer topics on unseen documents!
- LDA is a Bayesian version of PLSA
LDA
-
LDA
- Core idea: assume each document contains a mix of topics
- But the topic structure is hidden (latent)
- LDA infers the topic structure given the observed words and documents
- LDA produces soft clusters of documents (based on topic overlap), rather than hard clusters
- Given a trained LDA model, it can infer topics on new documents (not part of train data)

-
input
- A collection of documents
- Bag-of-words
- Good preprocessing practice:
- Remove stopwords
- Remove low and high frequency word types
- Lemmatisation
-
output
-
Topics: distribution over words in each topic

-
Topic assignment: distribution over topics in each document

-
-
learning
-
How do we learn the latent topics?
-
Two main family of algorithms:
- Variational methods
- Sampling-based methods
-
sampling method (Gibbs)
-
Randomly assign topics to all tokens in documents

-
Collect topic-word and document-topic co-occurrence statistics based on the assignments
-
first give some psudo-counts in every cell of two matrix(smoothing,no event is 0)

-
collect co-occurrence statistics

-
-
Go through every word token in corpus and sample a new topic:
-
delete current topic assigned to a word

-
update two matrices

-
compute the probability distribution to sample: P ( t i ∣ w , d ) ∝ P ( t i ∣ w ) P ( t i ∣ d ) P(t_i|w,d) \propto P(t_i|w)P(t_i|d) P(ti∣w,d)∝P(ti∣w)P(ti∣d) ( P ( t i ∣ w ) → P(t_i|w) \to P(ti∣w)→ topic-word, P ( t i ∣ d ) → P(t_i|d) \to P(ti∣d)→ document-topic)

- P ( t 1 ∣ w , d ) = P ( t 1 ∣ m o u s e ) × P ( t 1 ∣ d 1 ) = 0.01 0.01 + 0.01 + 2.01 × 1.1 1.1 + 1.1 + 2.1 P(t_1|w,d)=P(t_1|mouse)\times{P(t_1|d_1)}=\frac{0.01}{0.01+0.01+2.01}\times{\frac{1.1}{1.1+1.1+2.1}} P(t1∣w,d)=P(t1∣mouse)×P(t1∣d1)=0.01+0.01+2.010.01×1.1+1.1+2.11.1
-
sample randomly based on the probability distribution
-
-
Go to step 2 and repeat until convergence
- when to stop
- Train until convergence
- Convergence = model probability of training set becomes stable
- How to compute model probability?
- l o g P ( w 1 , w 2 , . . . , w m ) = l o g ∑ j = 0 T P ( w 1 ∣ t j ) P ( t j ∣ d w 1 ) + . . . + l o g ∑ j = 0 T P ( w m ∣ t j ) P ( t j ∣ d w m ) logP(w_1,w_2,...,w_m)=log\sum_{j=0}^TP(w_1|t_j)P(t_j|d_{w_1})+...+log\sum_{j=0}^TP(w_m|t_j)P(t_j|d_{w_m}) logP(w1,w2,...,wm)=log∑j=0TP(w1∣tj)P(tj∣dw1)+...+log∑j=0TP(wm∣tj)P(tj∣dwm)
- m = #word tokens
- P ( w 1 ∣ t j ) → P(w_1|t_j) \to P(w1∣tj)→ based on the topic-word co-occurrence matrix
- P ( t j ∣ d w 1 ) → P(t_j|d_{w_1}) \to P(tj∣dw1)→ based on the document-topic co-occurrence matrix
- infer topics for new documents
-
Randomly assign topics to all tokens in new/test documents

-
Update document-topic matrix based on the assignments; but use the trained topic-word matrix (kept fixed)

-
Go through every word in the test documents and sample topics: P ( t i ∣ w , d ) ∝ P ( t i ∣ w ) P ( t i ∣ d ) P(t_i|w,d) \propto P(t_i|w)P(t_i|d) P(ti∣w,d)∝P(ti∣w)P(ti∣d)
-
Go to step 2 and repeat until convergence
-
- hyper-parameters
-
T T T: number of topic

-
β \beta β: prior on the topic-word distribution
-
α \alpha α: prior on the document-topic distribution
-
Analogous to k in add-k smoothing in N-gram LM
-
Pseudo counts to initialise co-occurrence matrix:

-
High prior values → \to → flatter distribution

- a very very large value would lead to a uniform distribution
-
Low prior values → \to → peaky distribution

-
β \beta β: generally small (< 0.01)
- Large vocabulary, but we want each topic to focus on specific themes
-
α \alpha α: generally larger (> 0.1)
- Multiple topics within a document
-
-
-
Evaluation
- how to evaluate topic models
- Unsupervised learning → \to → no labels
- Intrinsic(内在的,固有的) evaluation:
- model logprob / perplexity(困惑度,复杂度) on test documents
- l o g L = ∑ W ∑ T l o g P ( w ∣ t ) P ( t ∣ d w ) logL=\sum_W\sum_TlogP(w|t)P(t|d_w) logL=∑W∑TlogP(w∣t)P(t∣dw)
- p p l = e x p − l o g L W ppl=exp^{\frac{-logL}{W}} ppl=expW−logL
- issues with perlexity
- More topics = better (lower) perplexity
- Smaller vocabulary = better perplexity
- Perplexity not comparable for different corpora, or different tokenisation/preprocessing methods
- Does not correlate with human perception of topic quality
- Extrinsic(外在的) evaluation the way to go:
- Evaluate topic models based on downstream task
- topic coherence
-
A better intrinsic evaluation method
-
Measure how coherent the generated topics (blue more coherent than red)

-
A good topic model is one that generates more coherent topics
-
- word intrusion
- Idea: inject one random word to a topic
- {farmers, farm, food, rice, agriculture} → \to → {farmers, farm, food, rice, cat, agriculture}
- Ask users to guess which is the intruder word
- Correct guess → \to → topic is coherent
- Try guess the intruder word in:
- {choice, count, village, i.e., simply, unionist}
- Manual effort; does not scale
- Idea: inject one random word to a topic
- PMI ≈ \approx ≈ coherence?
- High PMI for a pair of words → \to → words are correlated
- PMI(farm, rice) ↑ \uparrow ↑
- PMI(choice, village) ↓ \downarrow ↓
- If all word pairs in a topic has high PMI → \to → topic is coherent
- If most topics have high PMI → \to → good topic model
- Where to get word co-occurrence statistics for PMI?
- Can use same corpus for topic model
- A better way is to use an external corpus (e.g. Wikipedia)
- High PMI for a pair of words → \to → words are correlated
- PMI
- Compute pairwise PMI of top-N words in a topic
- P M I ( t ) = ∑ j = 2 N ∑ i = 1 j − 1 l o g P ( w i , w j ) P ( w i ) P ( w j ) PMI(t)=\sum_{j=2}^N\sum_{i=1}^{j-1}log\frac{P(w_i,w_j)}{P(w_i)P(w_j)} PMI(t)=∑j=2N∑i=1j−1logP(wi)P(wj)P(wi,wj)
- Given topic: {farmers, farm, food, rice, agriculture}
- Coherence = sum PMI for all word pairs:
- PMI(farmers, farm) + PMI(farmers, food) + … + PMI(rice, agriculture)
- variants
- Normalised PMI
- N P M I ( t ) = ∑ j = 2 N ∑ i = 1 j − 1 l o g P ( w i , w j ) P ( w i ) P ( w j ) − l o g P ( w i , w j ) NPMI(t)=\sum_{j=2}^N\sum_{i=1}^{j-1}\frac{log\frac{P(w_i,w_j)}{P(w_i)P(w_j)}}{-logP(w_i,w_j)} NPMI(t)=∑j=2N∑i=1j−1−logP(wi,wj)logP(wi)P(wj)P(wi,wj)
- conditional probability (proved not as good as PMI)
- L C P ( t ) = ∑ j = 2 N ∑ i = 1 j − 1 l o g P ( w i , w j ) P ( w i ) LCP(t)=\sum_{j=2}^N\sum_{i=1}^{j-1}log\frac{P(w_i,w_j)}{P(w_i)} LCP(t)=∑j=2N∑i=1j−1logP(wi)P(wi,wj)
- Normalised PMI
- example (PMI tends to favor rarer words, use NPMI to relieve this problem)
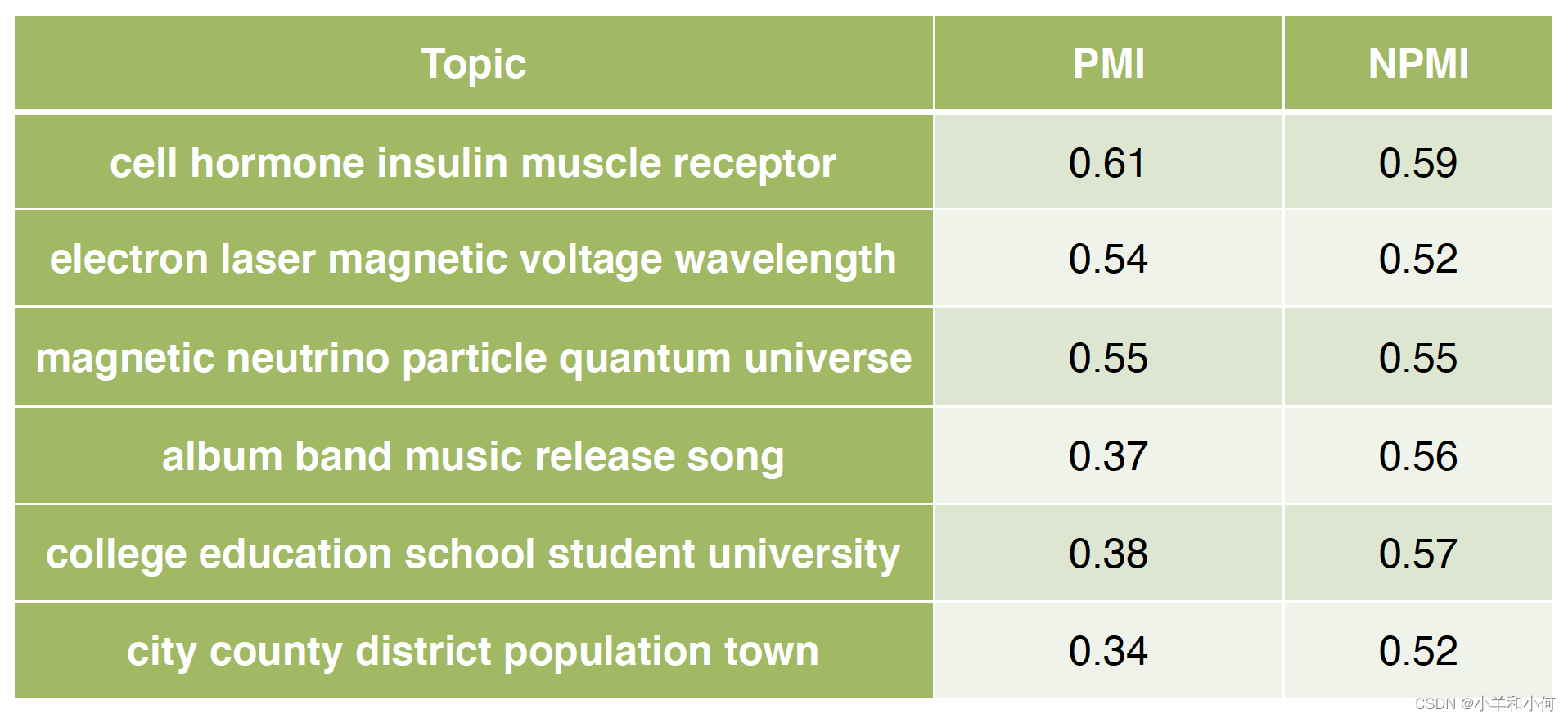
- Compute pairwise PMI of top-N words in a topic
Conclusion
- Topic model: an unsupervised model for learning latent concepts in a document collection
- LDA: a popular topic model
- Learning
- Hyper-parameters
- How to evaluate topic models?
- Topic coherence
相关文章:

Lecture 20 Topic Modelling
目录 Topic ModellingA Brief History of Topic ModelsLDAEvaluationConclusion Topic Modelling makeingsense of text English Wikipedia: 6M articlesTwitter: 500M tweets per dayNew York Times: 15M articlesarXiv: 1M articlesWhat can we do if we want to learn somet…...

ThreadPoolExecutor线程池
文章目录 一、ThreadPool线程池状态二、ThreadPoolExecutor构造方法三、Executors3.1 固定大小线程池3.2 带缓冲线程池3.3 单线程线程池 四、ThreadPoolExecutor4.1 execute(Runnable task)方法使用4.2 submit()方法4.3 invokeAll()4.4 invokeAny()4.5 shutdown()4.6 shutdownN…...

chatgpt赋能python:Python实践:如何升级pip
Python实践:如何升级pip Python作为一门高效的脚本语言,被广泛应用于数据分析、人工智能、Web开发等领域。而pip则是Python的包管理工具,是开发Python应用的必备工具。但是pip在使用过程中,有时候会出现版本不兼容或者出现漏洞等…...
【JavaEE进阶】mybatis
目录: 一、Mybatis是什么 三个映射关系如下图: 二、mybatis的使用(前置工作简单案例) 第一步:导入MAVEN依赖 第二步: 在spring项目当中新建数据源 第三步:新建一个实体类,是和…...
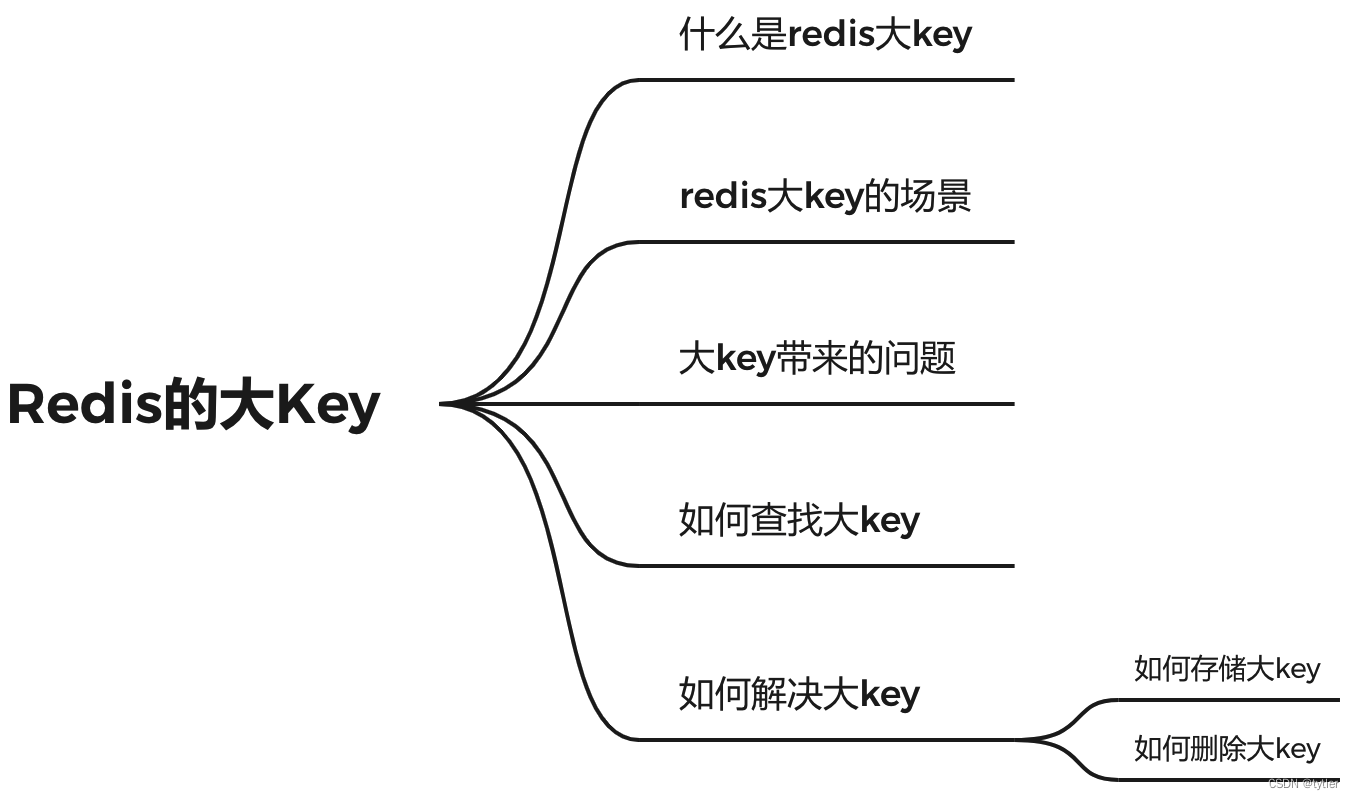
Redis的大key
什么是 redis 的大 key redis 的大 key 不是指存储在 redis 中的某个 key 的大小超过一定的阈值,而是该 key 所对应的 value 过大对于 string 类型来说,一般情况下超过 10KB 则认为是大 key;对于set、zset、hash 等类型来说,一般…...
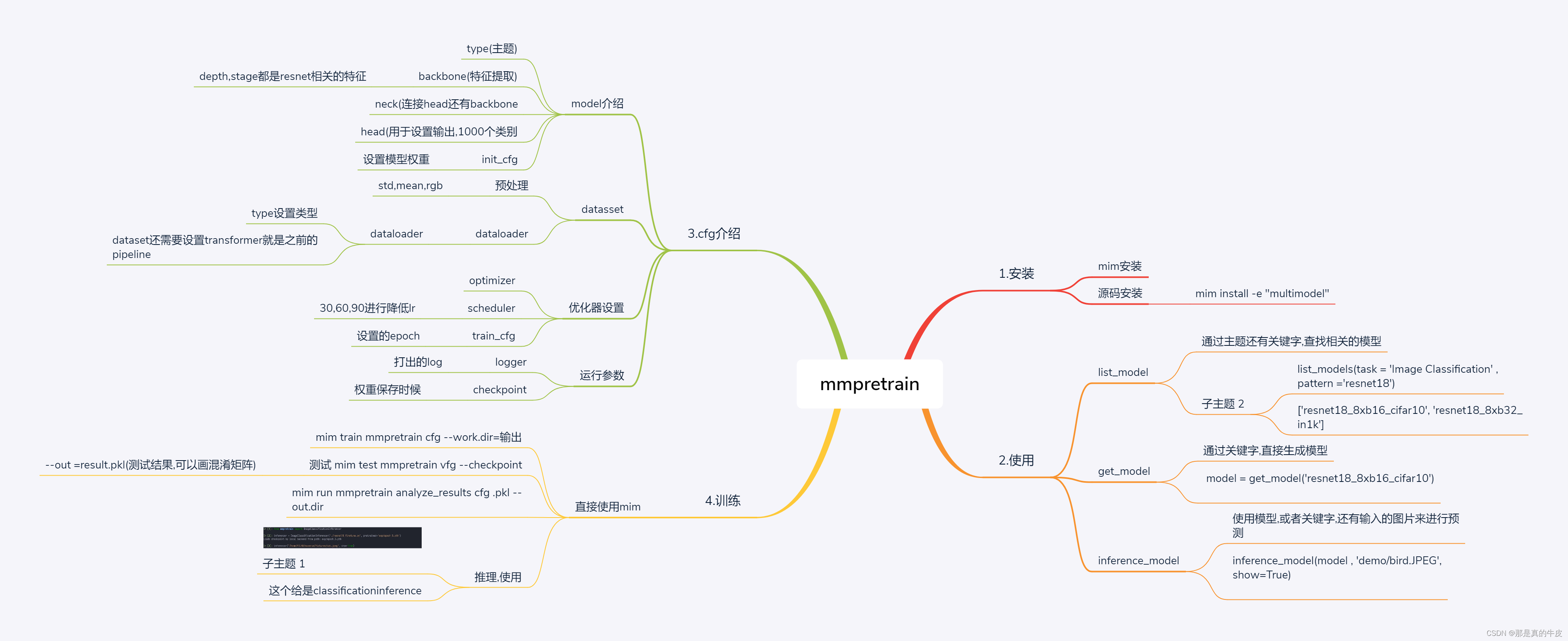
MMPretrain
title: mmpretrain实战 date: 2023-06-07 16:04:01 tags: [image classification,mmlab] mmpretrain实战 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ccTl9bOl-1686129437336)(null)] 主要讲解了安装,还有使用教程.安装教程直接参考官网.下面讲…...
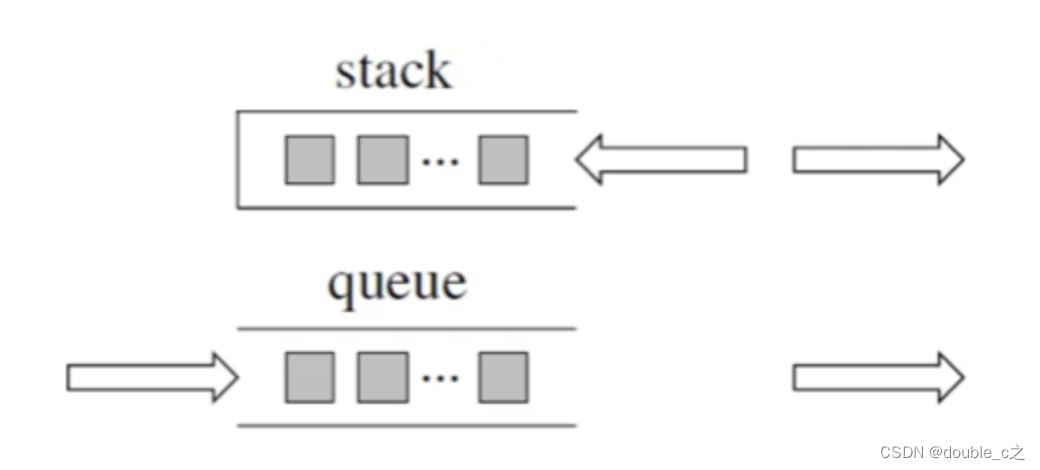
栈和队列(数据结构刷题)[一]-python
文章目录 前言一、原理介绍二、用栈实现队列1.操作2.思路 三、关于面试考察栈里面的元素在内存中是连续分布的么? 前言 提到栈和队列,大家可能对它们的了解只停留在表面,再深入一点,好像知道又好像不知道的感觉。本文我将从底层实…...

【备战秋招】JAVA集合
集合 前言 一方面, 面向对象语言对事物的体现都是以对象的形式,为了方便对多个对象 的操作,就要 对对象进行存储。 另一方面,使用Array存储对象方面具有一些弊端,而Java 集合就像一种容器,可以动态地把多…...

setState详解
this. setState( [partialState], [callback]) 1.[partialState] :支持部分状态更改 this, setState({ x:100 //不论总共有多少状态,我们只修改了x,其余的状态不动 });callback :在状态更改/视图更新完毕后触发执行,也可以说只要执行了setS…...

Qt5.12.6配置Android Arm开发环境(windows)
1. 安装jdk1.8 2.安装Android Studio 并安装 SDK 与NDK SDK Tools 选择 26.0.3 SDK Platform 选择 Android SDK Platform 26 NDK选择19版本 安卓ARM环境配置成功如下: JDK1.8 , SDK 26 , NDK 19 在安装QT时要选择 ARMv7(32位CPU)与ARM64-v8a(64位CPU) 选择支持android平台…...
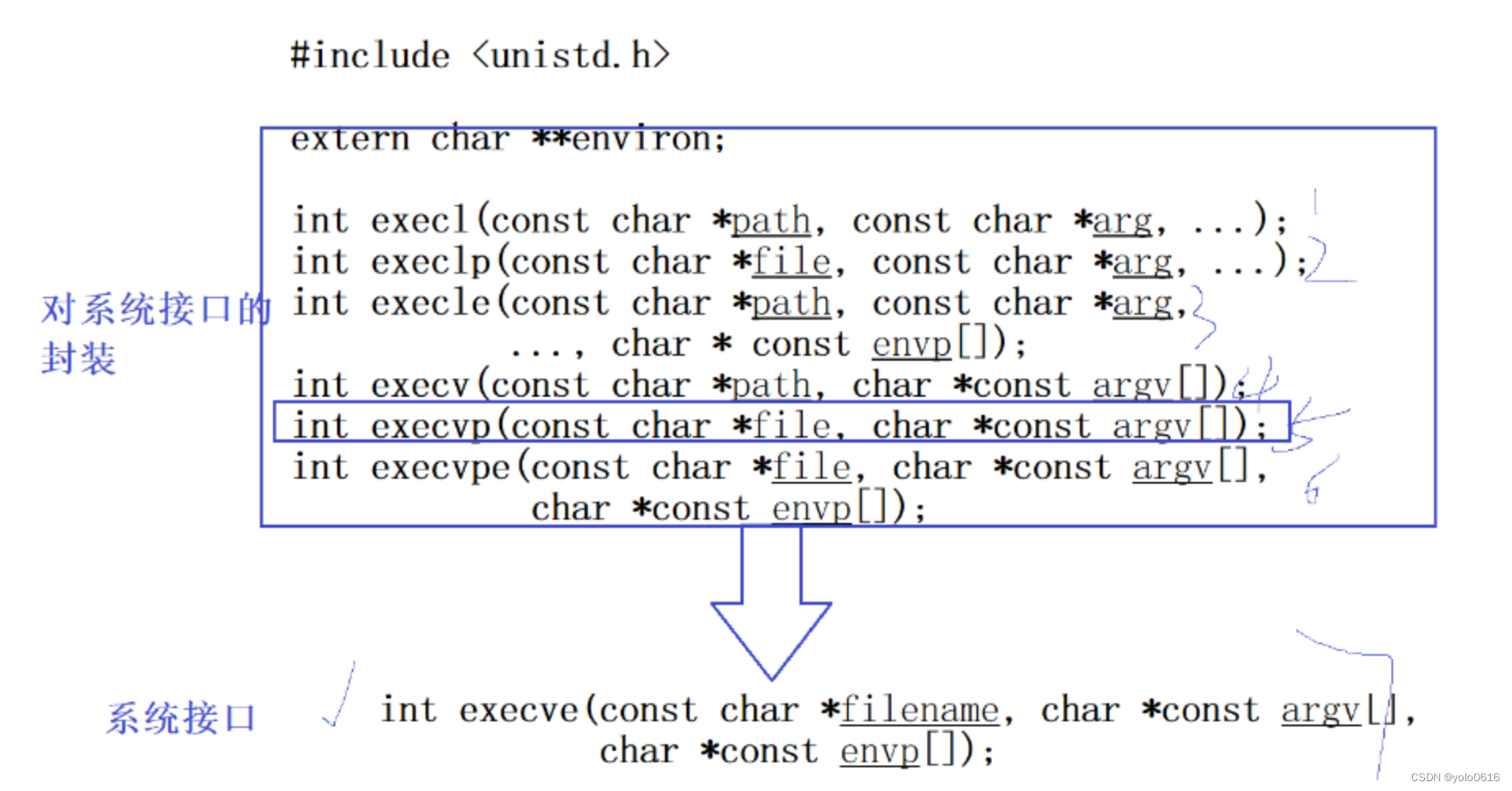
七、进程程序替换
文章目录 一、进程程序替换(一)概念(二)为什么程序替换(三)程序替换的原理(四)如何进行程序替换1. execl2. 引入进程创建——子进程执行程序替换,会不会影响父进程呢? &…...
C++核心编程——详解运算符重载
文章目录💬 一.运算符重载基础知识①基本概念②运算符重载的规则③运算符重载形式④运算符重载建议 二.常用运算符重载①左移(<<)和右移(>>)运算符重载1️⃣重载后函数参数是什么?2️⃣重载的函数返回类型是什么?3️⃣重载为哪种…...
2023年前端面试汇总-CSS
1. CSS基础 1.1. CSS选择器及其优先级 对于选择器的优先级: 1. 标签选择器、伪元素选择器:1; 2. 类选择器、伪类选择器、属性选择器:10; 3. id 选择器:100; 4. 内联样式:1000&a…...

Java调用Pytorch实现以图搜图(附源码)
Java调用Pytorch实现以图搜图 设计技术栈: 1、ElasticSearch环境; 2、Python运行环境(如果事先没有pytorch模型时,可以用python脚本创建模型); 1、运行效果 2、创建模型(有则可以跳过…...
【EasyX】实时时钟
目录 实时时钟1. 绘制静态秒针2. 秒针的转动3. 根据实际时间转动4. 添加时针和分针5. 添加表盘刻度 实时时钟 本博客介绍利用EasyX实现一个实时钟表的小程序,同时学习时间函数的使用。 本文源码可从github获取 1. 绘制静态秒针 第一步定义钟表的中心坐标center&a…...

基于XC7Z100的PCIe采集卡(GMSL FMC采集卡)
GMSL 图像采集卡 特性 ● PCIe Gen2.0 X8 总线; ● 支持V4L2调用; ● 1路CAN接口; ● 6路/12路 GMSL1/2摄像头输入,最高可达8MP; ● 2路可定义相机同步触发输入/输出; 优势 ● 采用PCIe主卡与FMC子…...
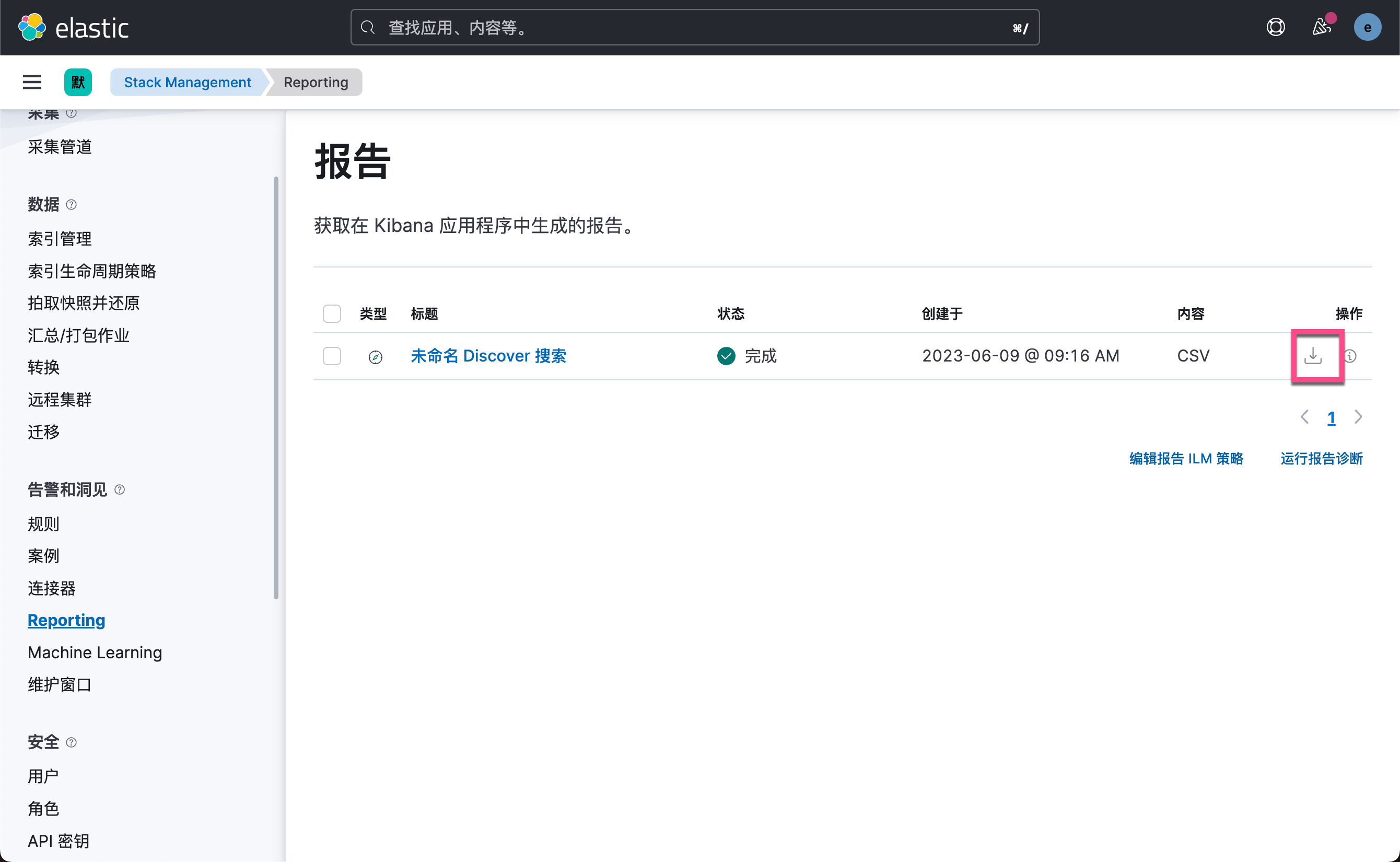
Kibana:使用 Kibana 自带数据进行可视化(一)
在今天的练习中,我们将使用 Kibana 自带的数据来进行一些可视化的展示。希望对刚开始使用 Kibana 的用户有所帮助。 前提条件 如果你还没有安装好自己的 Elastic Stack,你可以参考如下的视频来开启 Elastic Stack 并进行下面的练习。你可以开通阿里云检…...
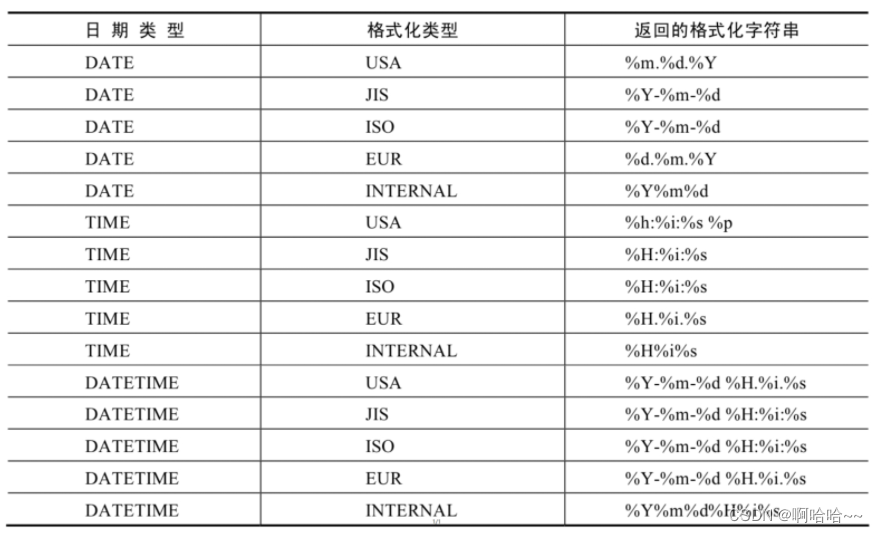
MySQL数据库基础 07
第七章 单行函数 1. 函数的理解1.1 什么是函数1.2 不同DBMS函数的差异1.3 MySQL的内置函数及分类 2. 数值函数2.1 基本函数2.2 角度与弧度互换函数2.3 三角函数2.4 指数与对数2.5 进制间的转换 3. 字符串函数4. 日期和时间函数4.1 获取日期、时间 4.2 日期与时间戳的转换 4.3 获…...

JVM | JVM垃圾回收
JVM | JVM垃圾回收 1、堆空间的基本结构2、内存分配和回收原则2.1、对象优先在 Eden 区分配2.2、大对象直接进入老年代2.3、长期存活的对象将进入老年代2.4、主要进行 gc 的区域2.5、空间分配担保3、死亡对象判断方法3.1、引用计数法3.2、可达性分析算法3.3、引用类型总结3.4、…...

avive零头撸矿
Avive 是一个透明的、自下而上替代自上而下的多元网络,旨在克服当前生态系统的局限性,实现去中心化社会。 aVive:一个基于 SBT 和市场的 deSoc,它使 dapps 能够与分散的位置 oracle 和 SBT 关系进行互操作。您的主权社交网络元宇宙…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...

spring Security对RBAC及其ABAC的支持使用
RBAC (基于角色的访问控制) RBAC (Role-Based Access Control) 是 Spring Security 中最常用的权限模型,它将权限分配给角色,再将角色分配给用户。 RBAC 核心实现 1. 数据库设计 users roles permissions ------- ------…...
