第七十天学习记录:高等数学:微分(宋浩板书)
微分的定义

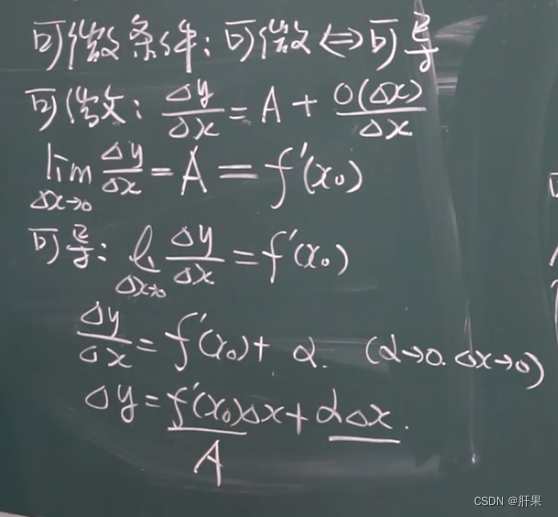
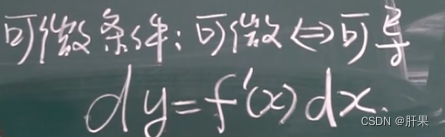
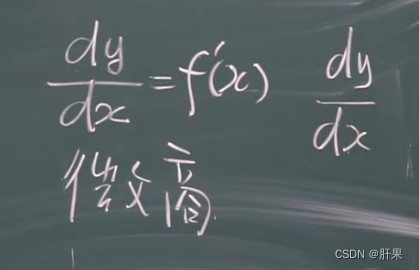
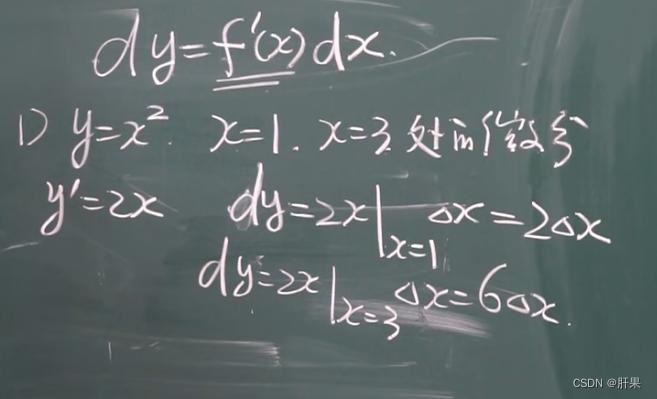
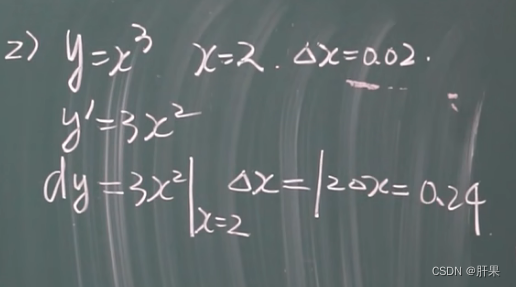
基本微分公式与法则
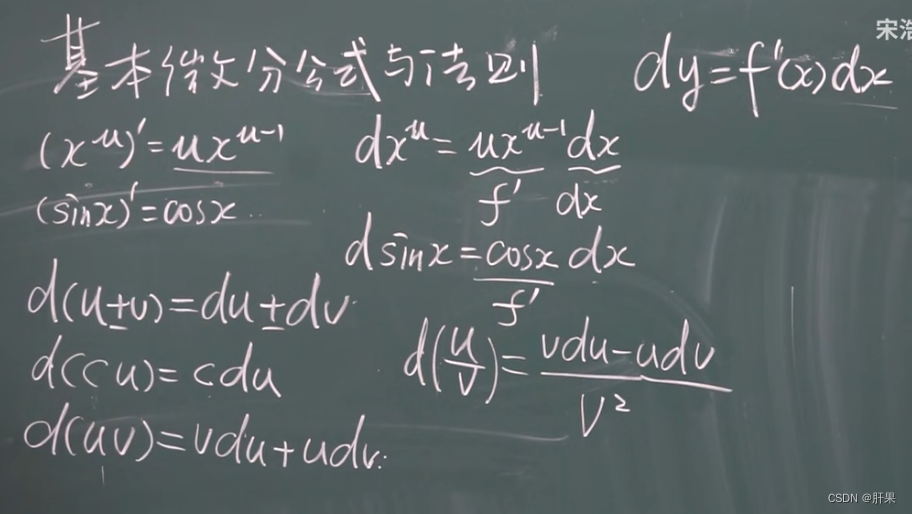
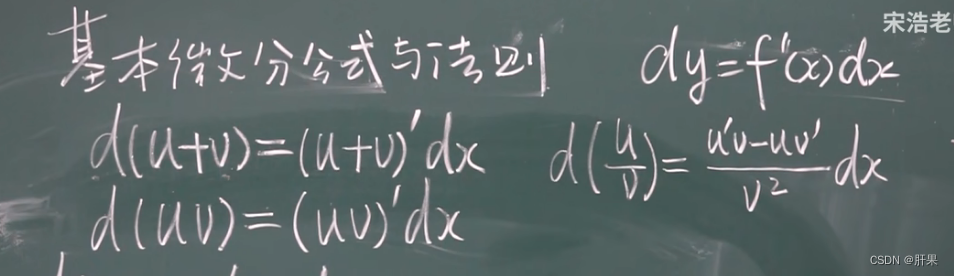
复合函数的微分
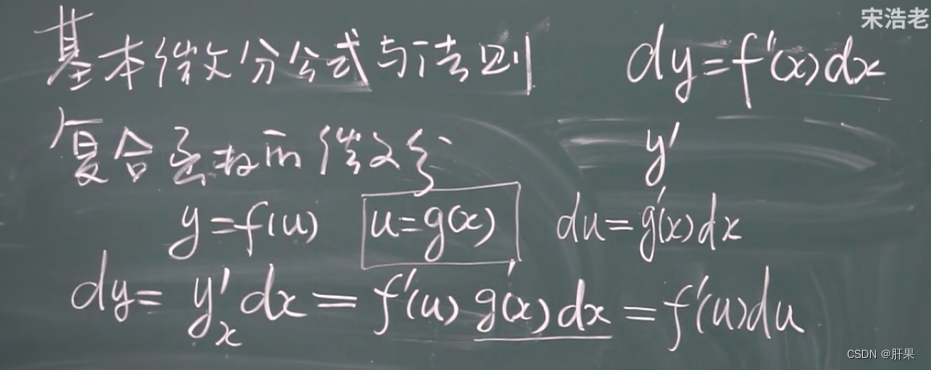
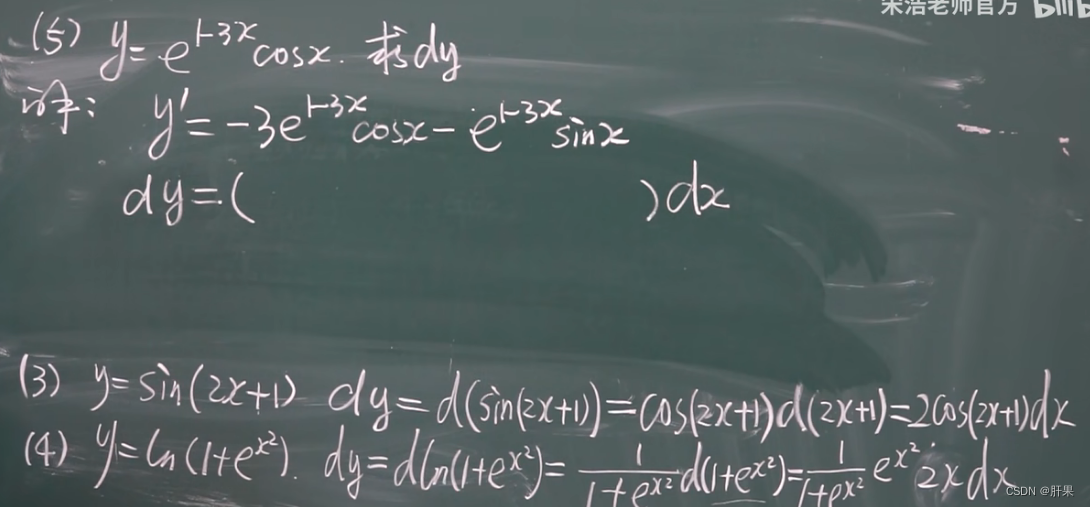
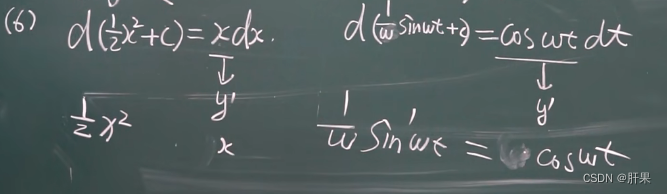
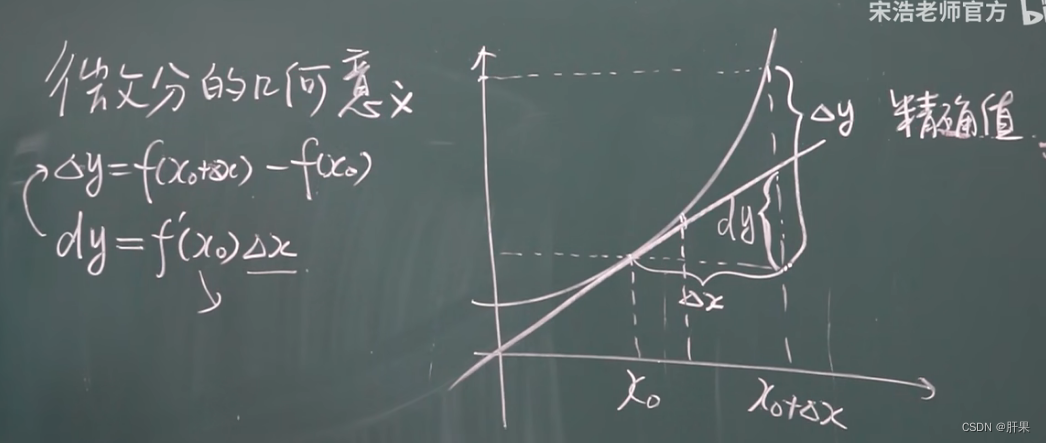
微分的几何意义
微分在近似计算中应用
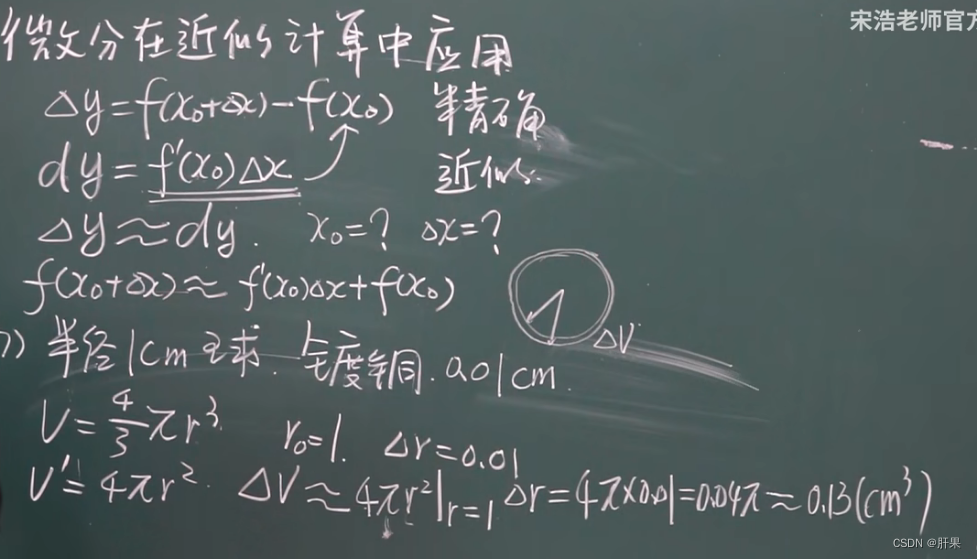

sin(x+y) = sin(x)cos(y) + cos(x)sin(y)可以用三角形的几何图形来进行证明。
假设在一个单位圆上,点A(x,y)的坐标为(x,y),点B(x’, y’)的坐标为(x’, y’)。则以两点为直角的直角三角形的斜边长为1,且所在的角为夹角x+y。
接下来,通过计算三角形中的各条边可以得到:
sin(x+y) = y’+y
cos(x+y) = x’+x
将cos x = x, sin x = y, cos y = x’ 和 sin y = y’ 代入上述公式得到:
sin(x+y) = sin(x)cos(y) + cos(x)sin(y)
至此,公式的正确性得到证明。
同时,我们还可以在单位圆上仿照上面的方法证明和差化积公式的正确性,这同样也是基于三角形的几何形式得到的。

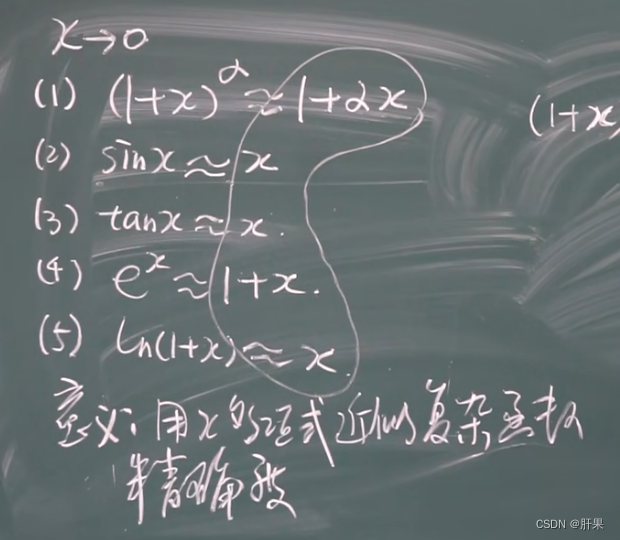
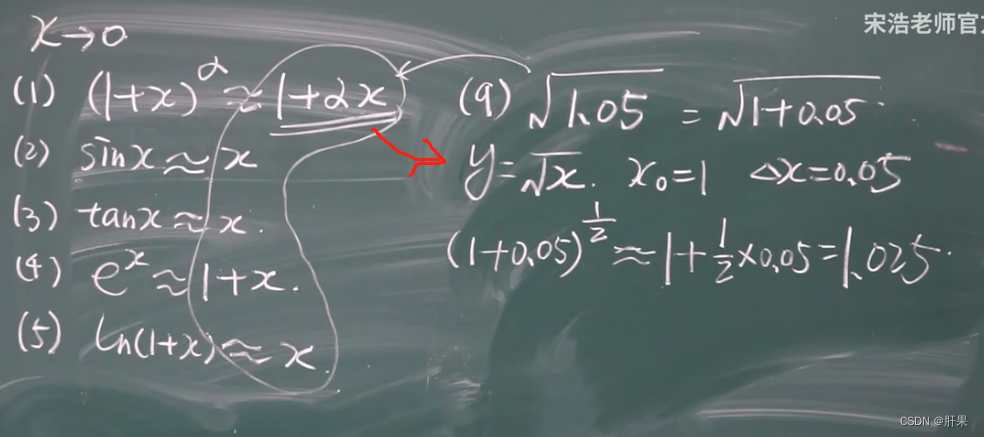
微分中值定理 罗尔定理




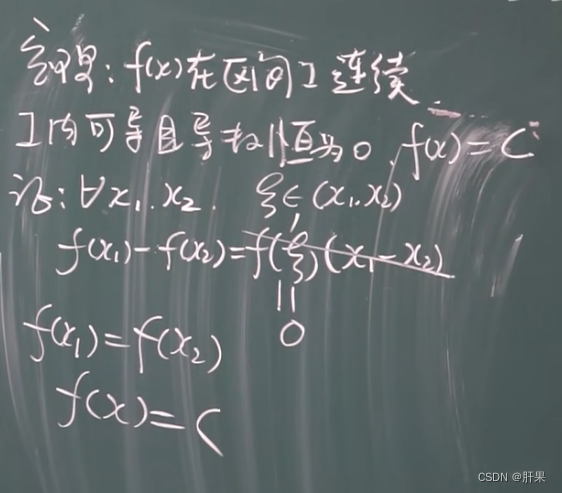
微积分中解决实际问题的过程一般包括两个步骤:微分和积分。
微分就是求导数,其本质是研究函数在某个点附近的局部变化,是一种用来描述函数变化情况的方法。而导数的定义是函数在某点处的变化速率,可以通过极限的方式准确地求解,不需要使用任何近似值。因此,导数的求解不需要近似值。
而微分的目的是为了研究函数在某个区间内的整体变化情况,例如函数的极值、拐点等。微分中经常需要计算函数的斜率,也就是导数。在一些情况下,我们无法直接求解导数,需要利用差商进行近似计算。这里的差商是指函数在两个点处的函数值之差与这两个点之间的距离之比,因此差商实际上是一种近似的导数计算方法。因此,微分中的近似计算需要使用差商这种近似的方法来实现。
另外,导数能够准确地描述函数在某点附近的局部变化,而微分则研究函数在整个区间内的整体变化情况。因此,在求解导数时,只需要关注函数在某点的变化情况,精度较高;而在微分过程中,则需要考虑整个区间内的变化情况,需要使用近似方法来近似计算。
柯西中值定理

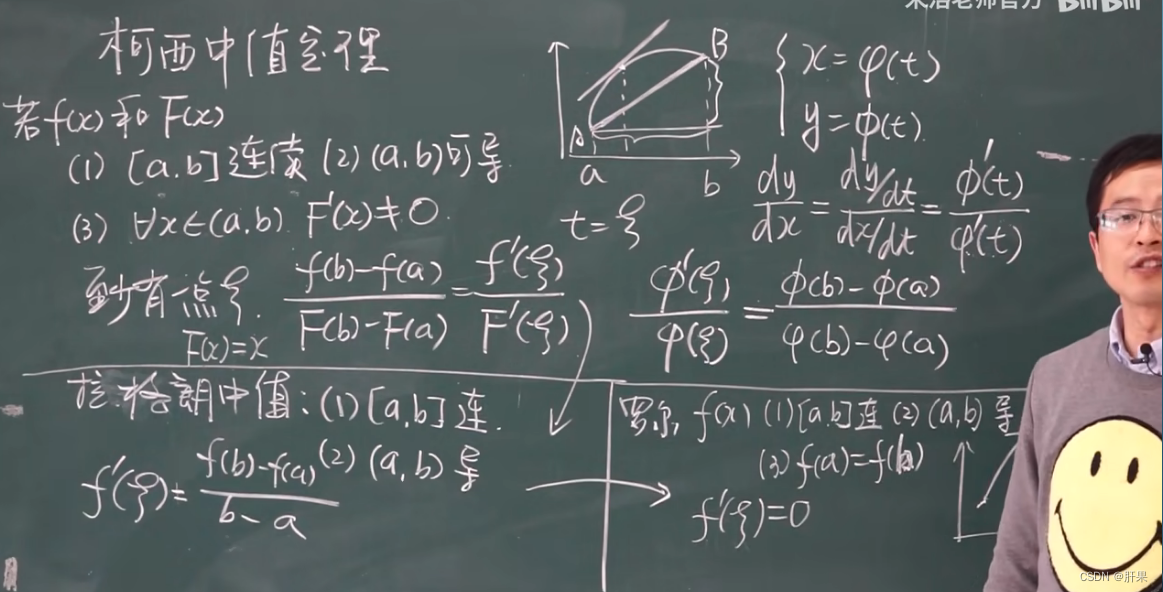
洛必达法则★★★★★
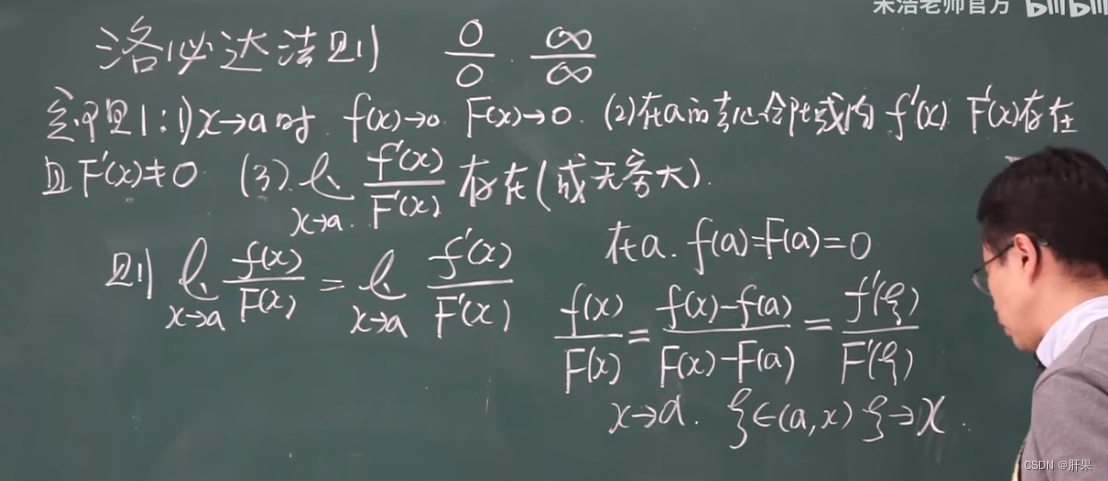

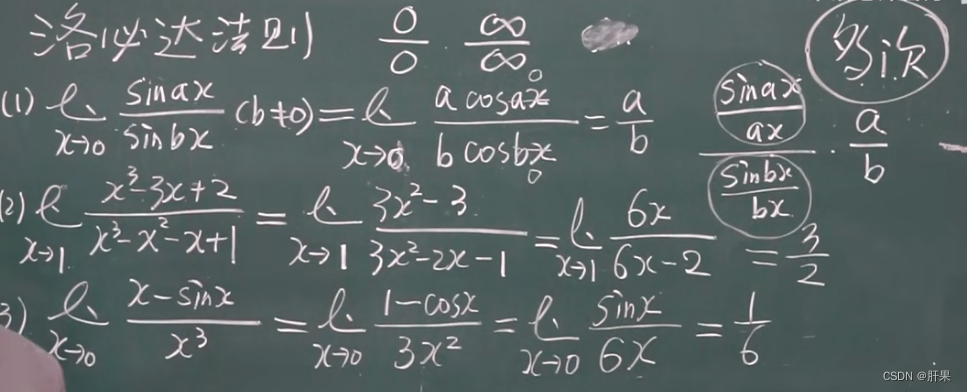


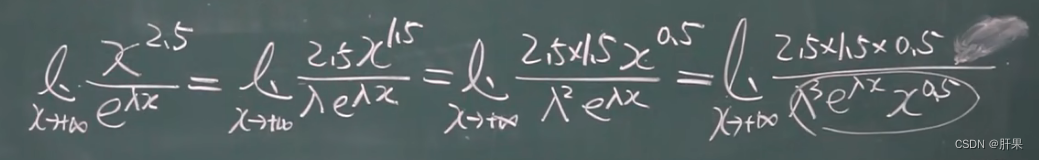
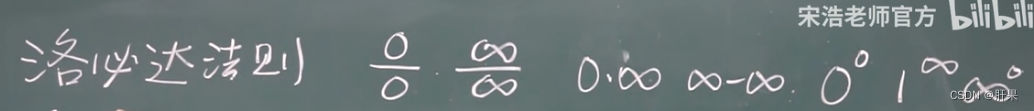
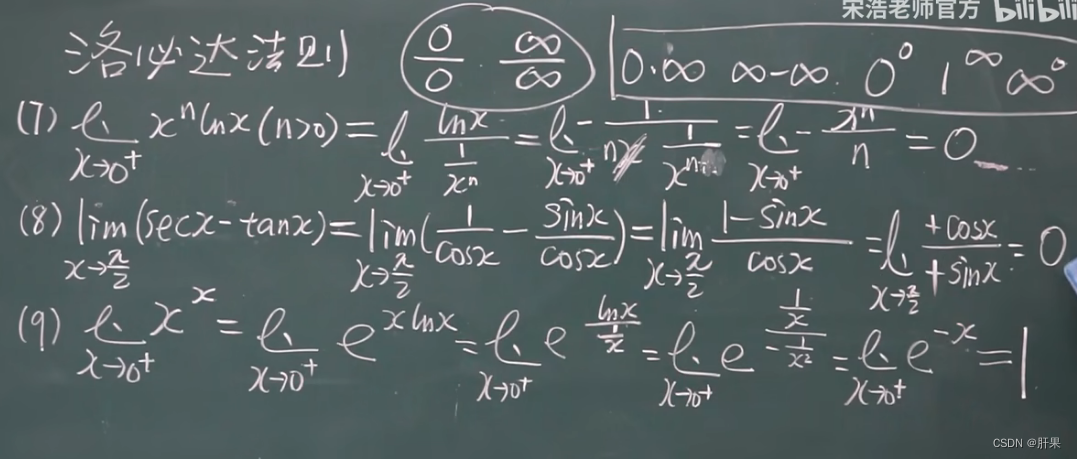

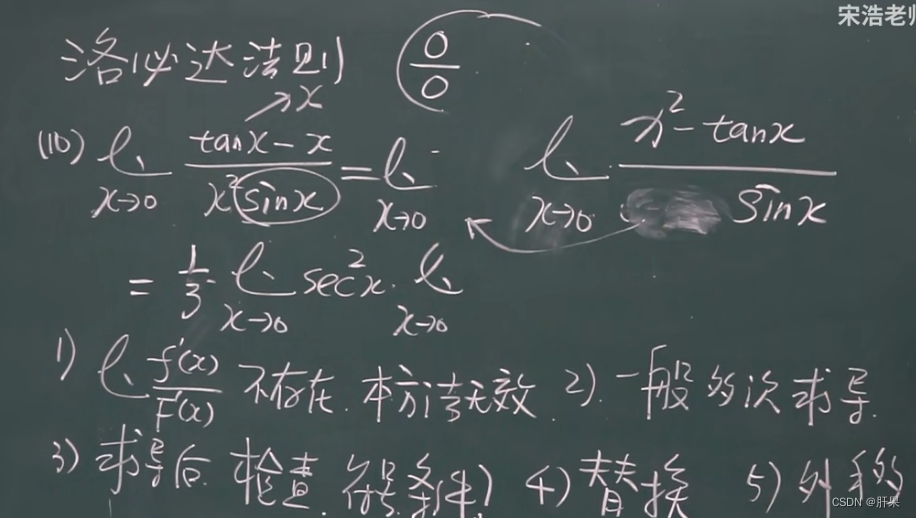
泰勒公式
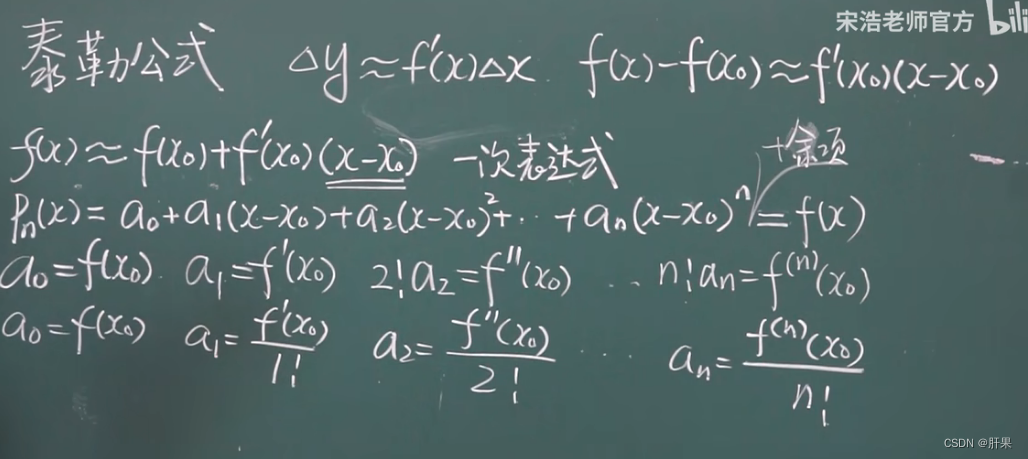
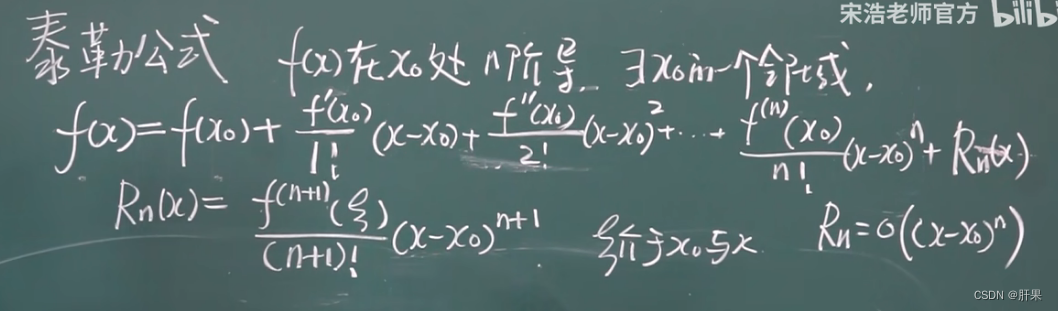

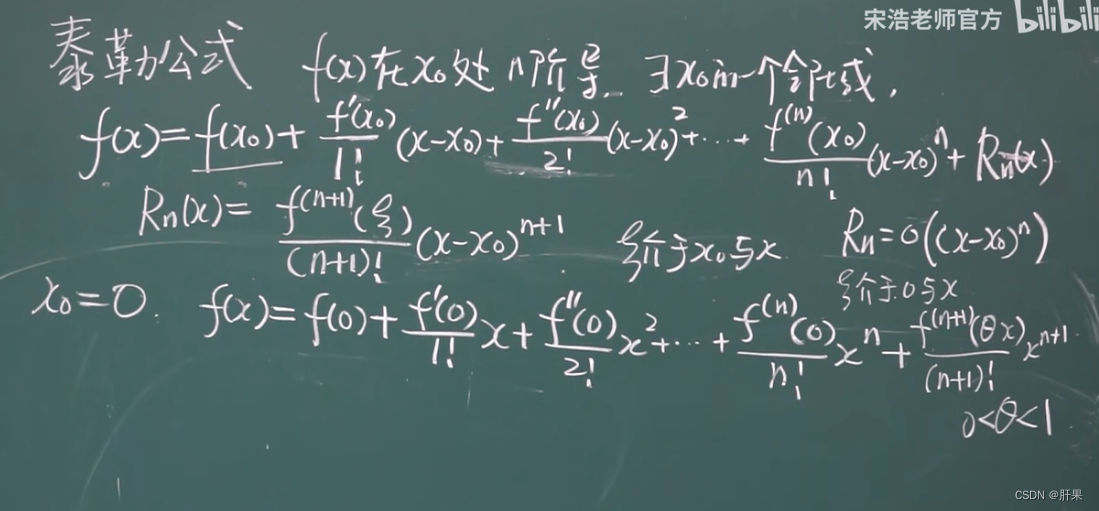
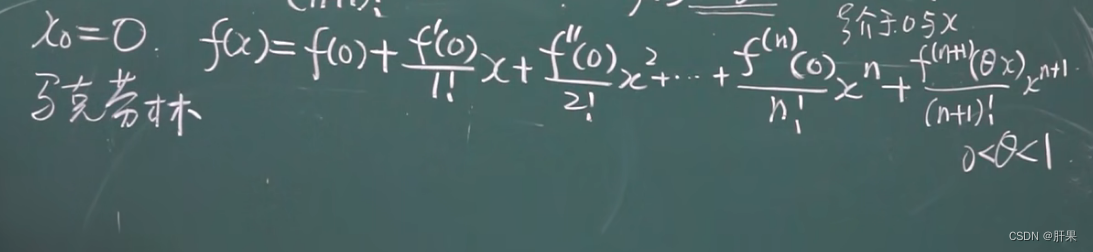


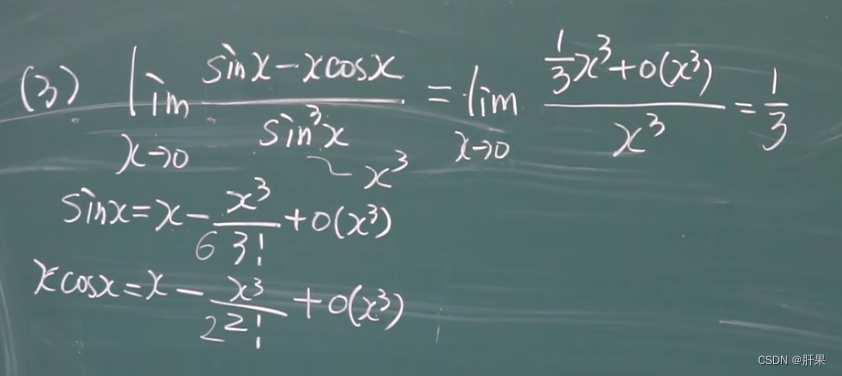
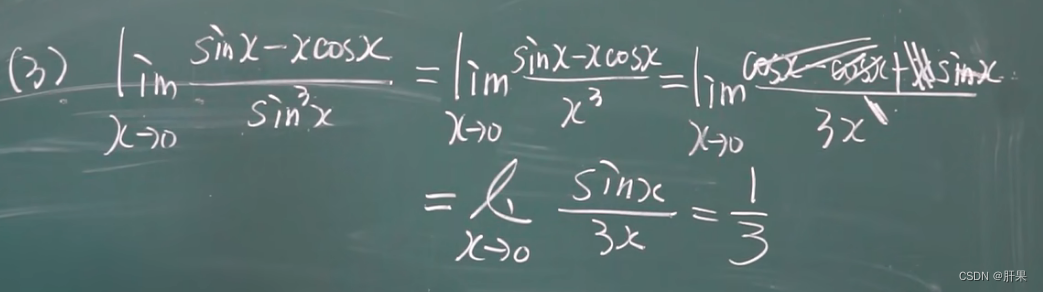
单调性


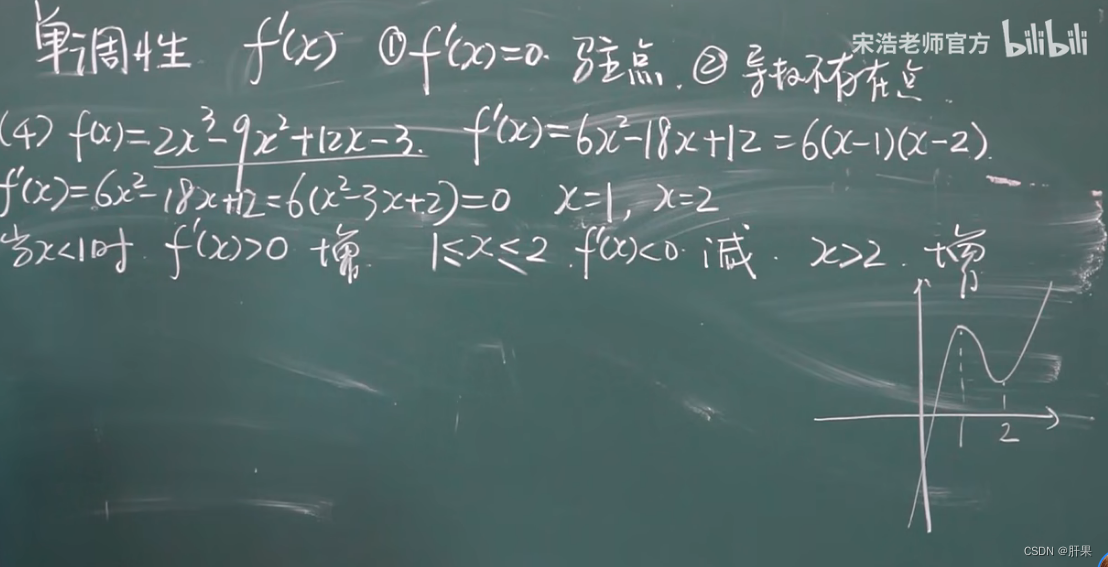





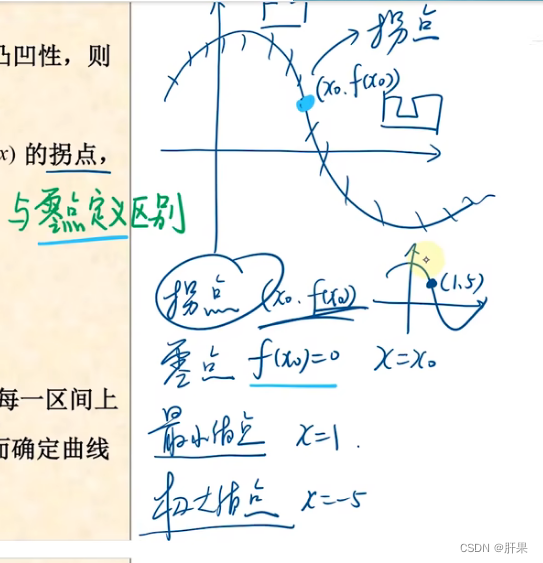


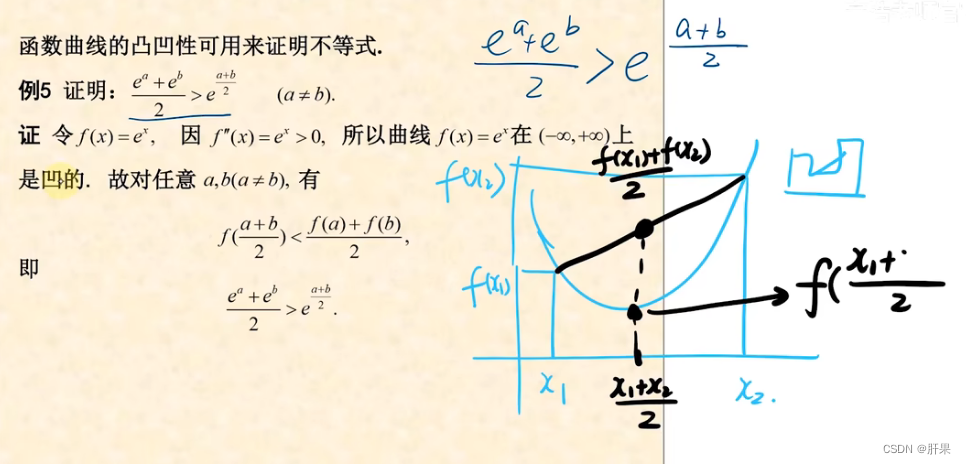
极值与其求法
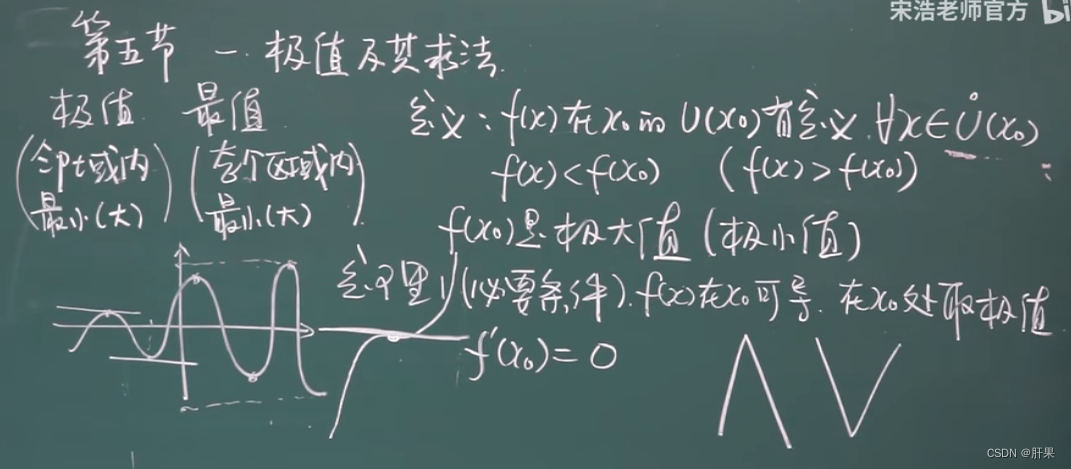
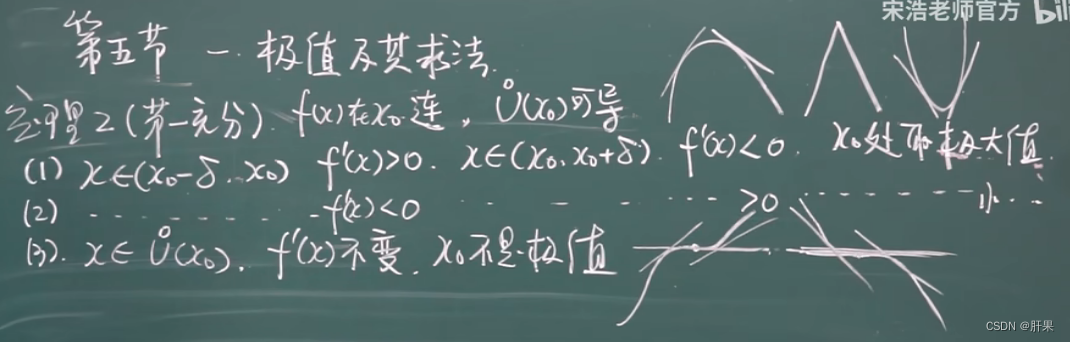



渐近线
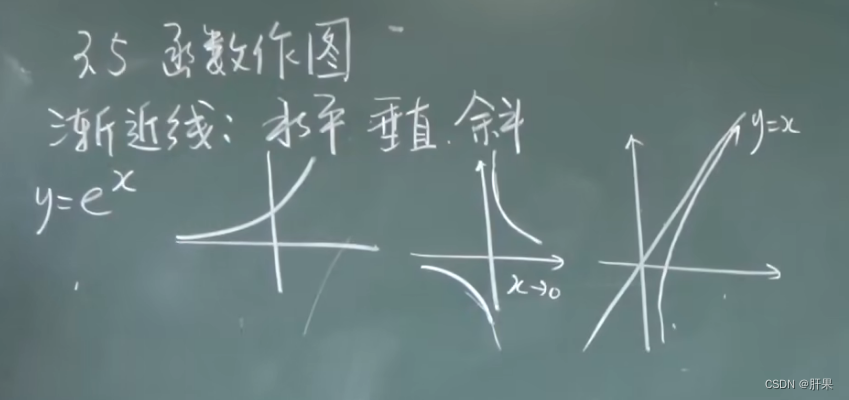
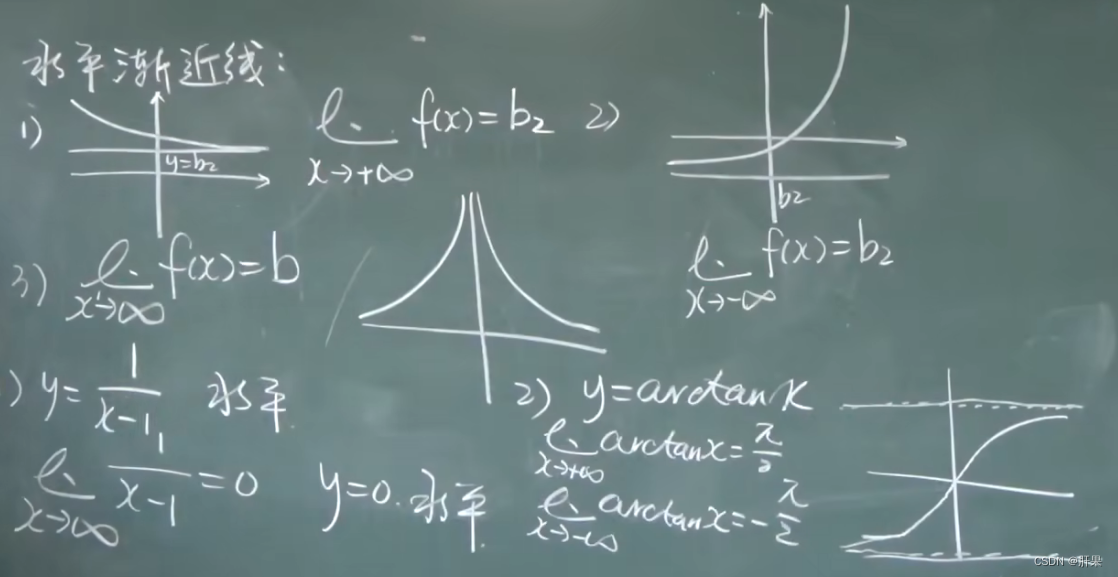
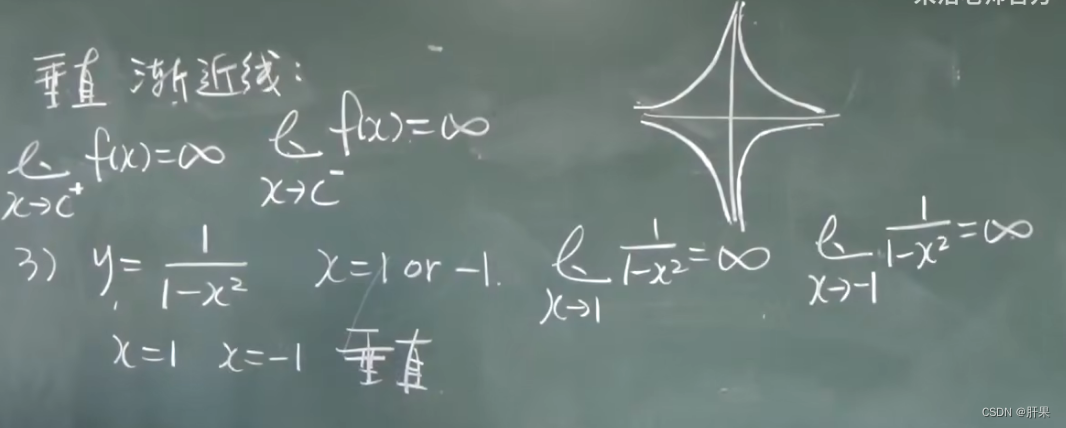
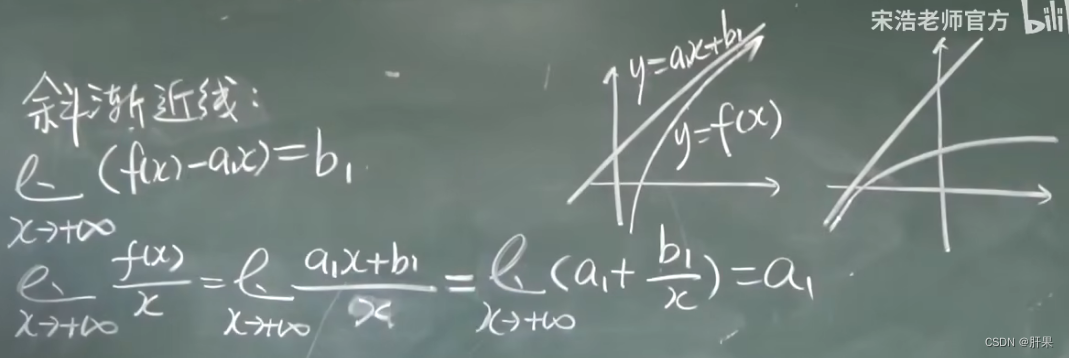
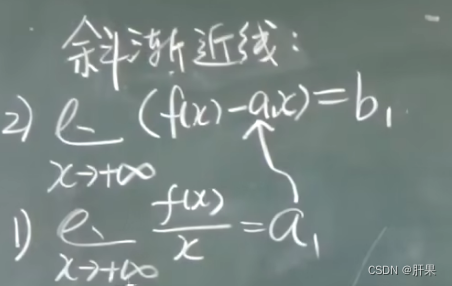
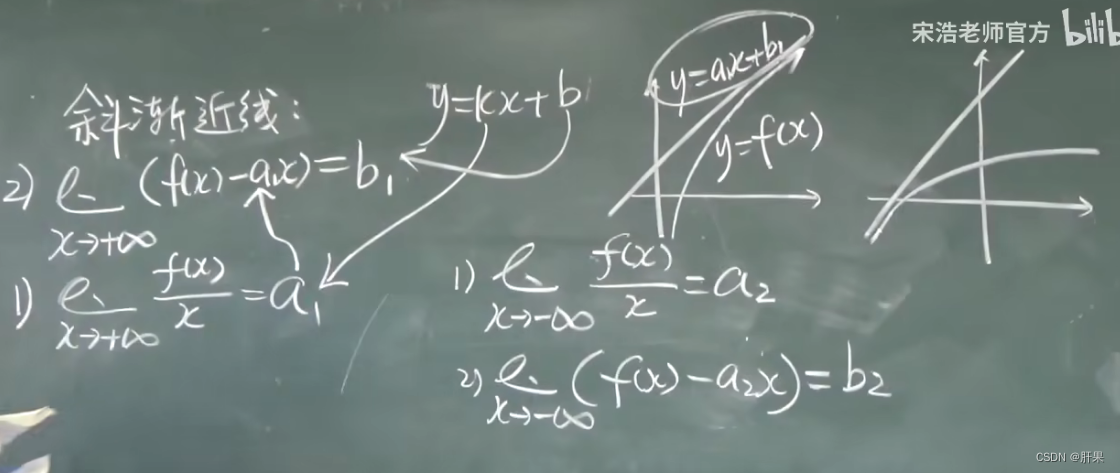
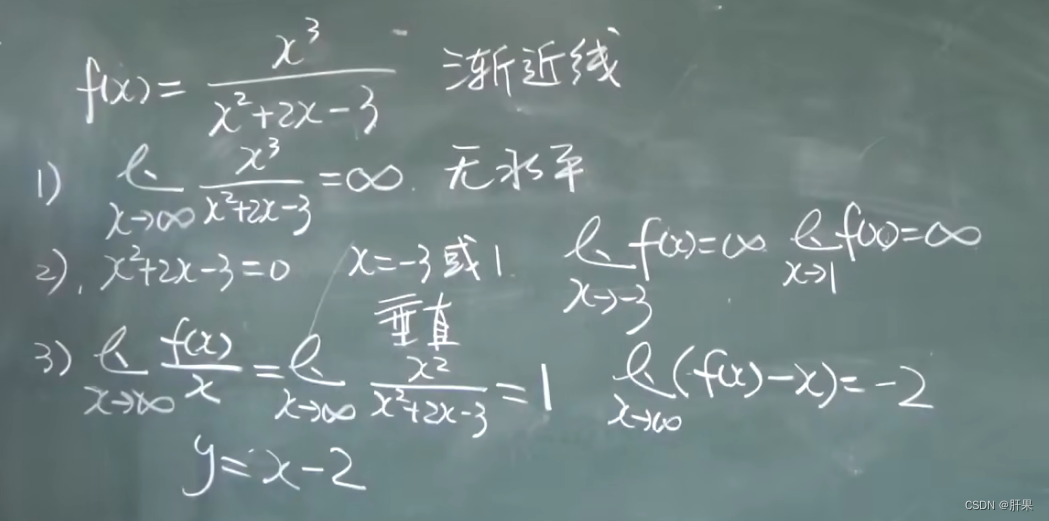
函数图形的绘制

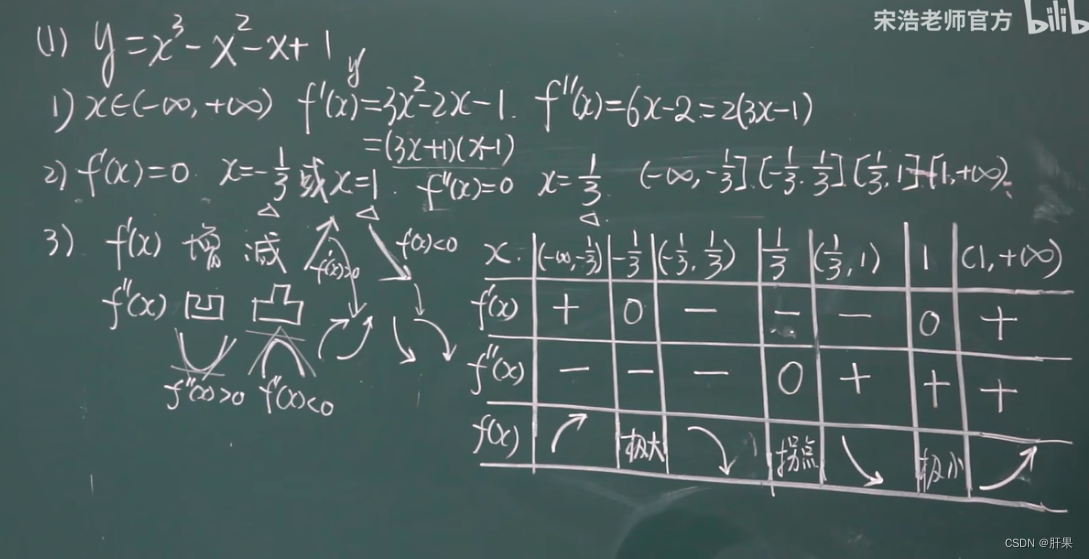
为什么偶函数求导就是奇函数?
设 f(x) 是一个偶函数,即 f(x) = f(-x)。则有:
f’(x) = lim(h→0)[f(x+h) - f(x)]/h
将 h 替换为 -h,得到:
f’(-x) = lim(-h→0)[f(-x+h) - f(-x)]/h
因为 f(x) 是偶函数,所以 f(-x+h) = f(-(x-h)) = f(x-h),且 f(-x) = f(x),可以得到:
f’(-x) = lim(h→0)[-f(x-h) + f(x)]/(-h)
因为减去一个数可以看作加上它的相反数,即 -f(x-h) = f(-(x-h)) = f(x+h),可以得到:
f’(-x) = lim(h→0)[f(x+h) - f(x)]/h = f’(x)
所以 f(x) 的导函数 f’(x) 是偶函数。
因此,若偶函数 f(x) 求导后得到的导函数为 f’(x),则 f’(x) 是奇函数。


这是二次方程标准形式,可以使用求根公式(也称为“二次公式”)求解。
二次公式:
对于二次方程 ax^2 + bx + c = 0,解的公式为:
x = (-b ± √(b^2 - 4ac)) / 2a
即,解为两个根:
x1 = (-b + √(b^2 - 4ac)) / 2a
x2 = (-b - √(b^2 - 4ac)) / 2a
其中±表示两种可能的符号(+或-),√表示算术平方根。
根的性质:
-
当 b^2 - 4ac > 0 时,方程有两个不相等的实数根。
-
当 b^2 - 4ac = 0 时,方程有两个相等的实数根。
-
当 b^2 - 4ac < 0 时,方程没有实数根,但有两个共轭复根。
注意:
求根公式对于系数 a 不为 0 的二次方程适用,对于 a = 0 的情况,此时方程不再是二次方程,而是一次方程。
另外,在实际计算过程中,要注意避免出现计算误差或溢出等情况,需要采取适当的数值稳定性措施。

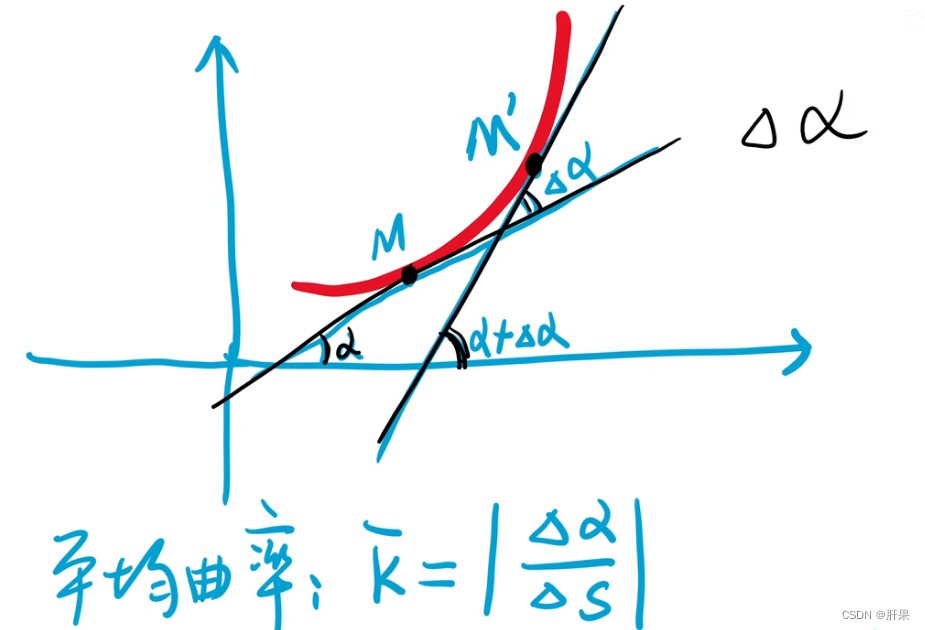
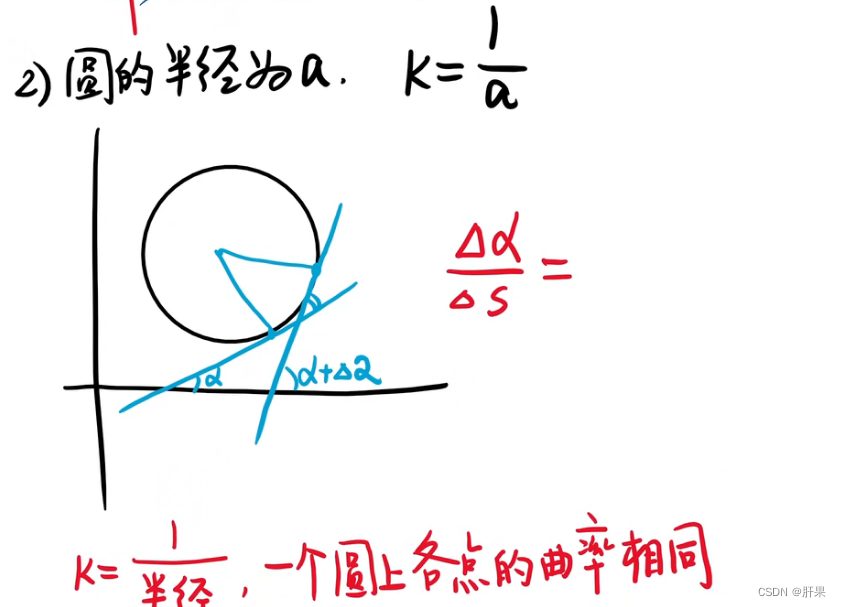
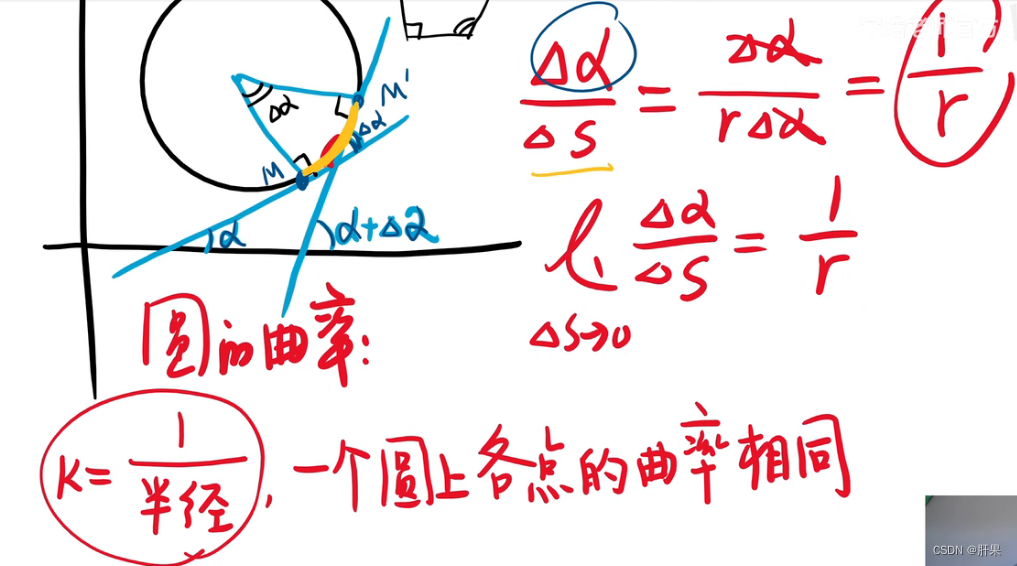
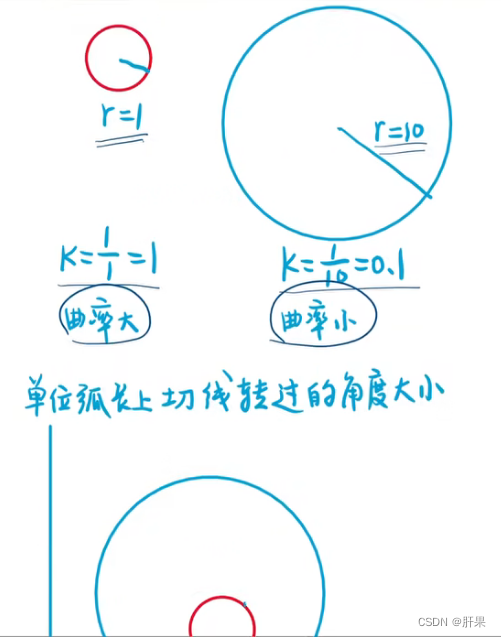
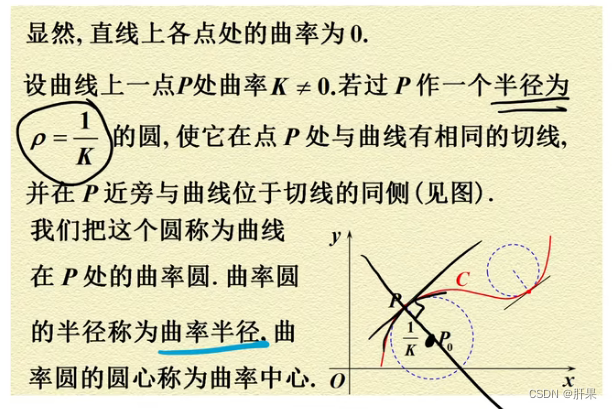
曲率
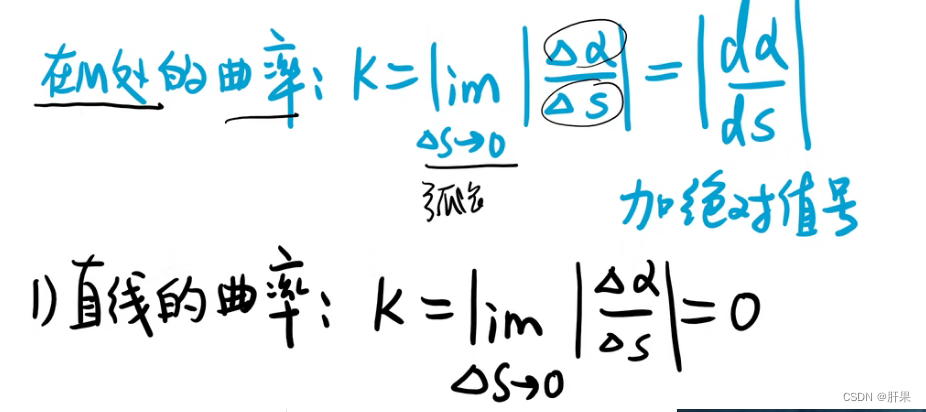
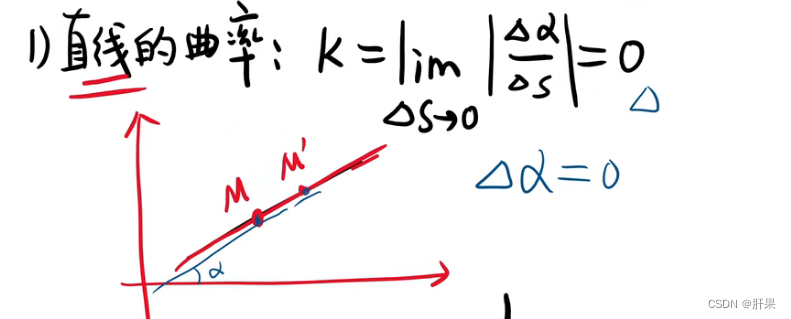


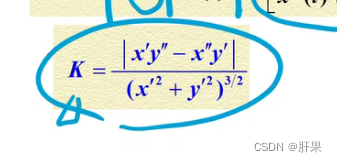

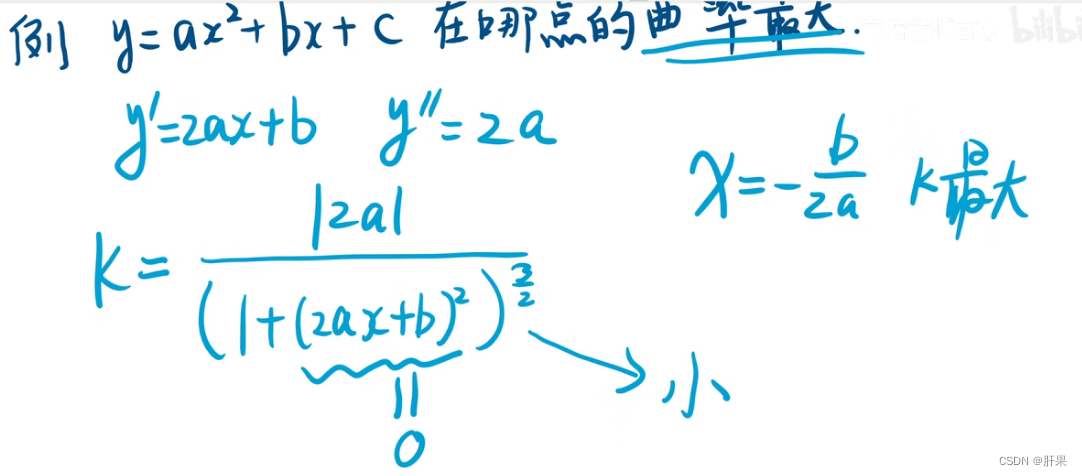
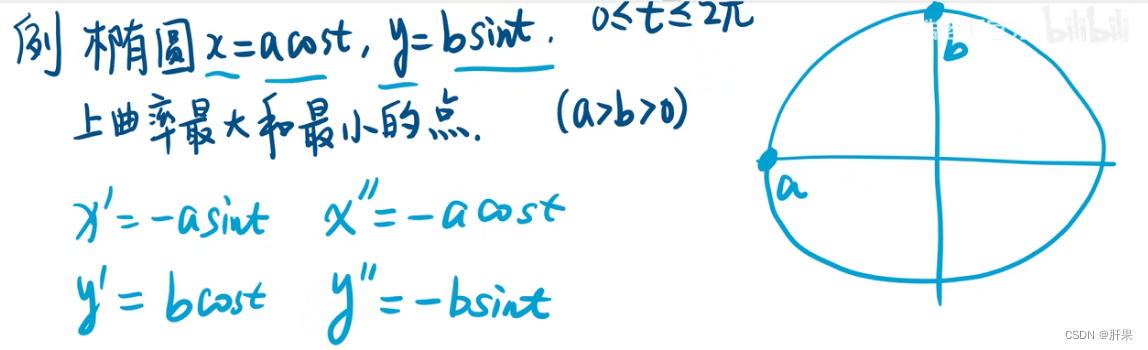

相关文章:

第七十天学习记录:高等数学:微分(宋浩板书)
微分的定义 基本微分公式与法则 复合函数的微分 微分的几何意义 微分在近似计算中应用 sin(xy) sin(x)cos(y) cos(x)sin(y)可以用三角形的几何图形来进行证明。 假设在一个单位圆上,点A(x,y)的坐标为(x,y),点B(x’, y’)的坐标为(x’, y’)。则以两点…...

Jmeter
目录 一、jmeter 安装 二、jmeter 介绍 1、jmeter是什么? 2、jmeter 用来做什么? 3、优点 4、缺点 5、jmeter 目录介绍 ①_bin 目录介绍 ② docs 目录 — — 接口文档目录 ③ extras目录 — — 扩展插件目录 ④ lib 目录 — — 所用到的插件目录 ⑤ lic…...

Flutter 学习 之 时间转换工具类
Flutter 学习之时间转换工具类 在 Flutter 应用程序开发中,处理时间戳是非常常见的需求。我们通常需要将时间戳转换为人类可读的日期时间格式。为了实现这一点,我们可以创建一个时间转换工具类。 实现方法 以下是一个简单的时间转换工具类的示例&…...
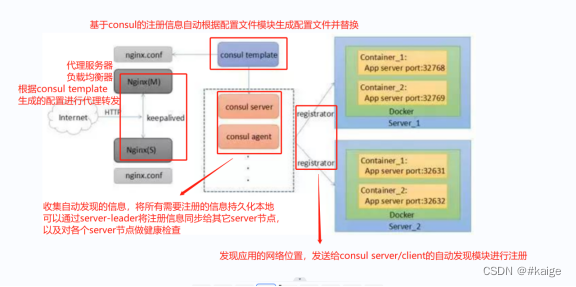
docker consul
docker consul的容器服务更新与发现 服务注册与发现是微服务架构中不可或缺的重要组件,起始服务都是单节点的,不保障高可用性,也不考虑服务的承载压力,服务之间调用单纯的通过接口访问的,直到后来出现多个节点的分布式…...
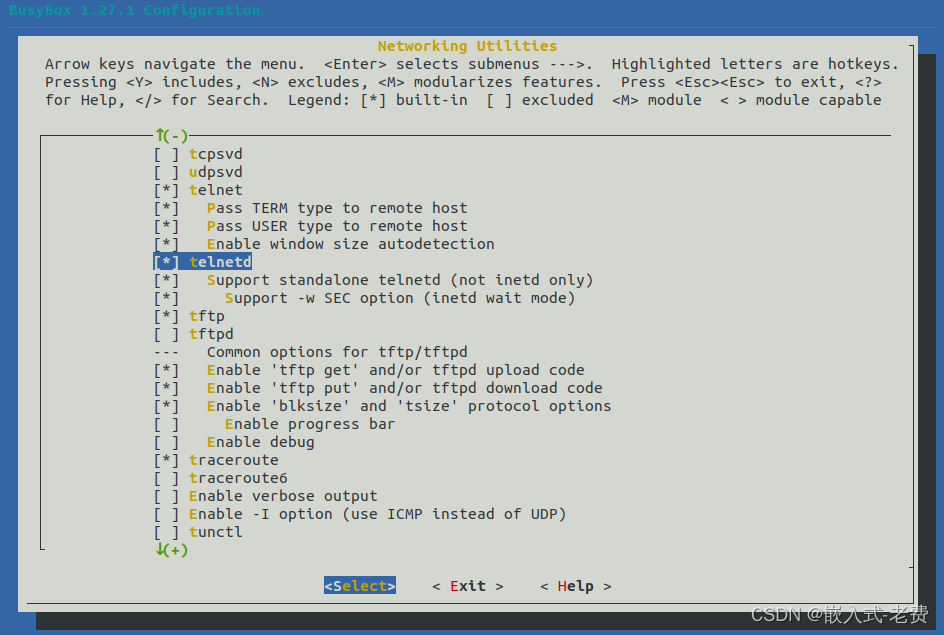
全志V3S嵌入式驱动开发(开发环境再升级)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 前面我们陆陆续续开发了差不多有10个驱动,涉及到网口、串口、音频和视频等几个方面。但是整个开发的效率还是比较低的。每次开发调试的…...

ChatGPT:人工智能助手的新时代
ChatGPT:人工智能助手的新时代 文章目录 ChatGPT:人工智能助手的新时代引言ChatGPT的原理GPT-3.5架构概述预训练和微调过程生成式对话生成技术 ChatGPT的应用场景智能助理客服机器人虚拟角色教育辅助创意生成个性化推荐 ChatGPT的优势ChatGPT的使用技巧与…...

【面试】二、Java补充知识
JVM中的存储 JVM的五块存储区: 方法区(线程共享) 方法区用来存储类的各种信息(类名、方法信息等)、静态变量、常量和编译后的代码也存储在方法区中 方法区中也存在运行时常量池 常量池中会存放程序运行时生成的各种…...

LISTENER、TNSNAMES和SQLNET配置文件
LISTENER、TNSNAMES和SQLNET配置文件 用户连接验证listener.ora文件配置监听日志local_listener参数 tnsnames.ora文件配置 sqlnet.ora文件配置 用户连接验证 Oracle数据库中用户有三种常见的登录验证方式: 通过操作系统用户验证:必须是在数据库服务器…...
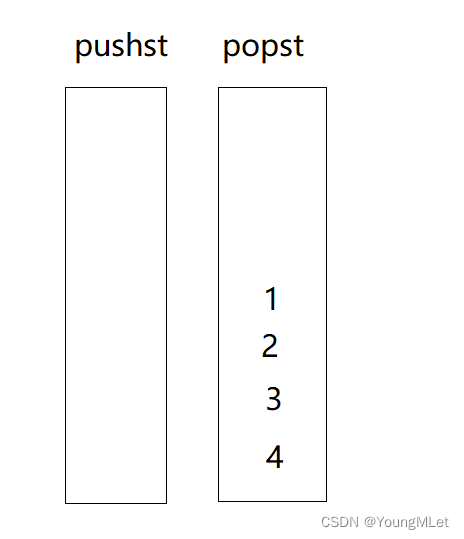
【Leetcode -225.用队列实现栈 -232.用栈实现队列】
Leetcode Leetcode -225.用队列实现栈Leetcode -232.用栈实现队列 Leetcode -225.用队列实现栈 题目:仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。 …...
悟道3.0全面开源!LeCun VS Max 智源大会最新演讲
夕小瑶科技说 原创 作者 | 小戏 2023 年智源大会如期召开! 这场汇集了 Geoffery Hinton、Yann LeCun、姚期智、Joseph Sifakis、Sam Altman、Russell 等一众几乎是 AI 领域学界业界“半壁江山”的大佬们的学术盛会,聚焦 AI 领域的前沿问题,…...
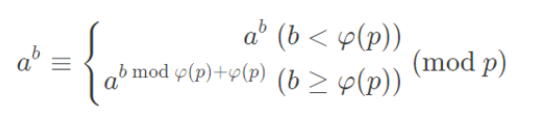
2023蓝桥杯大学A组C++决赛游记+个人题解
Day0 发烧了一晚上没睡着,感觉鼻子被打火机烧烤一样难受,心情烦躁 早上6点起来吃了个早饭,思考能力完全丧失了,开始看此花亭奇谭 看了六集,准备复习数据结构考试,然后秒睡 一睁眼就是下午2点了 挂了个…...

wkhtmltopdf踩坑记录
1. 不支持writing-mode。 需求是文字纵向排列,内容从左到右,本来用的是writing-mode: tb-rl;,插件转pdf后发现失效。 解决方法: 让每一列文字单独用一个div容器包裹,对它的宽度进行限制,控制每一行只能出现…...

贪心算法part2 | ● 122.买卖股票的最佳时机II ● 55. 跳跃游戏 ● 45.跳跃游戏II
文章目录 122.买卖股票的最佳时机II思路思路代码官方题解困难 55. 跳跃游戏思路思路代码官方题解代码困难 45.跳跃游戏II思路思路代码困难 今日收获 122.买卖股票的最佳时机II 122.买卖股票的最佳时机II 思路 局部最优:将当天价格和前一天比较,价格涨…...

[C++]异常笔记
我不怕练过一万种腿法的对手,就怕将一种腿法 练一万次的对手。 什么是C的异常 在C中,异常处理通常使用try-catch块来实现。try块用于包含可能会抛出异常的代码,而catch块用于捕获并处理异常。当异常被抛出时,程序会跳过try块中未执行…...

浅谈一级机电管道设计中的压力与介质温度
管道设计是工程设计中的一个非常重要的部分,管道的设计需要考虑到许多因素,其中就包括管道设计压力分类和介质温度分类。这两个因素是在设计管道时必须非常严格考虑的, 首先是管道设计压力分类。在管道设计中,根据工作要求和要传输…...
使用 macvlan 网络)
Docker网络模型(八)使用 macvlan 网络
使用 macvlan 网络 一些应用程序,特别是传统的应用程序或监控网络流量的应用程序,期望直接连接到物理网络。在这种情况下,你可以使用 macvlan 网络驱动为每个容器的虚拟网络接口分配一个MAC地址,使其看起来像一个直接连接到物理网…...
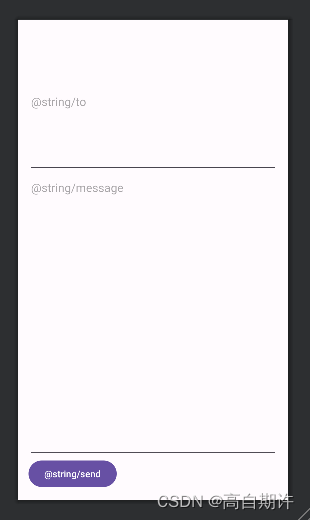
控制视图内容的位置
文本域中的提示内容在默认情况下是垂直居中的,要改变文本在文本域中的位置,可以使用android:gravity来实现。 利用android:gravity可以指定如何在视图中放置视图内容,例如,如何在文本域中放置文本。 如果希望视图文本显示在上方&a…...

【分布式系统与一致性协议】
分布式系统与一致性协议 CAP原理APCPCA总结BASE理论 一致性拜占庭将军问题 分布式系统是一个硬件或软件组件分布在不同的网络计算机上,彼此之间仅仅通过消息传递进行通信和协调的系统。 分布式系统的设计目标一般包含如下: 可用性:可用性是分…...

音视频领域的未来发展方向展望
文章目录 音视频领域的未来发展方向全景音视频技术虚拟现实和增强现实的区别 人工智能技术可视化智能分析智能语音交互图像识别和视频分析技术 语音处理智能推荐技术远程实时通信 流媒体技术未来方向 音视频领域的未来发展方向 全景音视频技术:全景音视频技术是近年…...
时间同步/集群时间同步/在线/离线
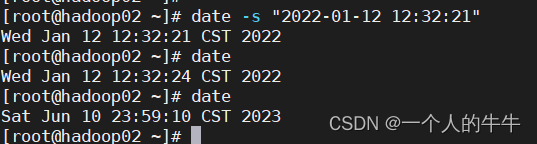
目录 一、能够连接外网 二、集群不能连接外网--同步其它服务器时间 一、能够连接外网 1.介绍ntp时间协议 NTP(Network Time Protocol)网络时间协议,是用来使计算机时间同步的一种协议,它可以使计算机对其服务器或时钟源做同步…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...
