数学模型:Python实现非线性规划
上篇文章:整数规划
文章摘要:非线性规划的Python实现。
参考书籍:数学建模算法与应用(第3版)司守奎 孙玺菁。
PS:只涉及了具体实现并不涉及底层理论。学习底层理论以及底层理论实现:可以参考1.最优化模型与算法——基于Python实现 渐令 粱锡军2.算法导论(原书第3版)Thomas H.Cormen Charles E.Leiserson、Ronald L.Rivest Clifford Stein
文章声明:如有发现错误,还望批评指正。
文章目录
- 非线性规划简述
- 非线性规划典例
- 蒙特卡洛随机模拟
非线性规划简述
线性规划可行域内一定有解并且可以通过单纯形法或内点法找到。由于线性规划是凸问题所以第一篇文章使用ECOS第二篇文章使用GLOK_ML是合理的。非线性规划由于没有通用的求解方法从而难以优化。但是某些特定形式的非线性规划问题可被优化或者可以找到一些近似的解。
非线性规划典例
这应该是最优化的内容范畴,我们这里不作讨论。我们这里介绍蒙特卡洛随机模拟。
蒙特卡洛随机模拟
参考书籍例2.9
目标函数
max y = x 1 2 + x 2 2 + 3 x 3 2 + 4 x 4 2 + 2 x 5 2 − 8 x 1 − 2 x 2 − 3 x 3 − x 4 − 2 x 5 \max y=x_1^2+x_2^2+3x_3^2+4x_4^2+2x_5^2-8x_1-2x_2-3x_3-x_4-2x_5 maxy=x12+x22+3x32+4x42+2x52−8x1−2x2−3x3−x4−2x5
约束条件
0 ≤ x i ≤ 99 , i = 1 , 2 , … , 5 0\leq x_i\leq99,i=1,2,\dots,5 0≤xi≤99,i=1,2,…,5
x 1 + x 2 + x 3 + x 4 + x 5 ≤ = 400 x_1+x_2+x_3+x_4+x_5\leq=400 x1+x2+x3+x4+x5≤=400
x 1 + 2 x 2 + 2 x 3 + x 4 + 6 x 5 ≤ 800 x_1+2x_2+2x_3+x_4+6x_5\leq800 x1+2x2+2x3+x4+6x5≤800
2 x 1 + x 2 + 6 x 3 ≤ = 200 2x_1+x_2+6x_3\leq=200 2x1+x2+6x3≤=200
x 3 + x 4 + 5 x 5 ≤ 200 x_3+x_4+5x_5\leq200 x3+x4+5x5≤200
from random import randint
def fun():lt=[randint(0,99) for _ in range(5)]if lt[0]+lt[1]+lt[2]+lt[3]+lt[4]>400:return Noneif lt[0]+2*lt[1]+2*lt[2]+lt[3]+6*lt[4]>800:return Noneif 2*lt[0]+lt[1]+6*lt[2]>200:return Noneif lt[2]+lt[3]+5*lt[4]>200:return Nonereturn lt[0]**2+lt[1]**2+3*lt[2]**2+4*lt[3]**2+2*lt[4]**2-8*lt[0]-2*lt[1]-3*lt[2]-lt[3]-2*lt[4]
n=pow(10,6);x=-float("inf")
for _ in range(n):f=fun()if f and f>x:x=f
print(x)
PS:30秒以内可以跑完。
相关文章:

数学模型:Python实现非线性规划
上篇文章:整数规划 文章摘要:非线性规划的Python实现。 参考书籍:数学建模算法与应用(第3版)司守奎 孙玺菁。 PS:只涉及了具体实现并不涉及底层理论。学习底层理论以及底层理论实现:可以参考1.最优化模型与算法——基于…...
使用 bridge 网络)
Docker网路模型(四)使用 bridge 网络
使用 bridge 网络 在计算机网络中,一个 bridge(网桥)是一个链路层设备,负责在不同的网段之间转发信息。 bridge 可以是真实的硬件设备也可以是由宿主机底层提供的软件模拟设备。 在 Docker 中,bridge 网络使用了软件…...
)
数据结构与算法之美 | 排序(2)
归并排序(Merge Sort) 基本思想: 如果要排序一个数组,我们先把数组从中间分成前后两部分,然后对前后两部分分别排序,再将排好序的两部分合并在一起,这样整个数组就都有序了。 def merge_sort…...

【外企面试系列】必备口语短语与例句 - A系列
a big headache令人头痛的事情 I have a big headache from all the noise. (我因为噪音而头痛。)The paperwork is a big headache for me. (对我来说,文书工作是件头痛的事情。) a fraction of 一部分 She ate only a fraction of her meal. (她只吃了一部分饭…...
Java使用Opencv进行大图找小图并使用其找图功能进行bilibili视频下载案例
Java使用Opencv进行大图找小图并使用其找图功能进行bilibili视频下载案例 一、Opencv大图找小图说明二、Opencv的window安装1.下载windows下的安装包2.安装3.Java中Opencv加载测试 三、Java中通过Opencv进行模板匹配大图找小图四、进行多图查找五:案例下载bilibili视…...

肠道健康从核心菌属开始:肠道菌群的关键
谷禾健康 5月29日,是世界肠道健康日。肠道是人体最重要的消化系统之一,与人体健康紧密相关。而肠道菌群作为肠道重要组成部分,在肠道健康中发挥着重要的作用。 编辑 由于基因、环境、饮食、药物等因素的影响,每个人的肠道菌群都…...
的搭建与实战应用)
深度学习实战37-NASNet(具有自动搜索能力的神经网络模型)的搭建与实战应用
大家好,我是微学AI,今天给大家介绍一下深度学习实战37-NASNet(具有自动搜索能力的神经网络模型)的搭建与实战应用,NASNet是由Google Brain团队开发的一种具有自动搜索能力的神经网络模型,利用强化学习和进化算法等技术来自动地搜索最优的神经网络架构。NASNet模型的设计灵感…...
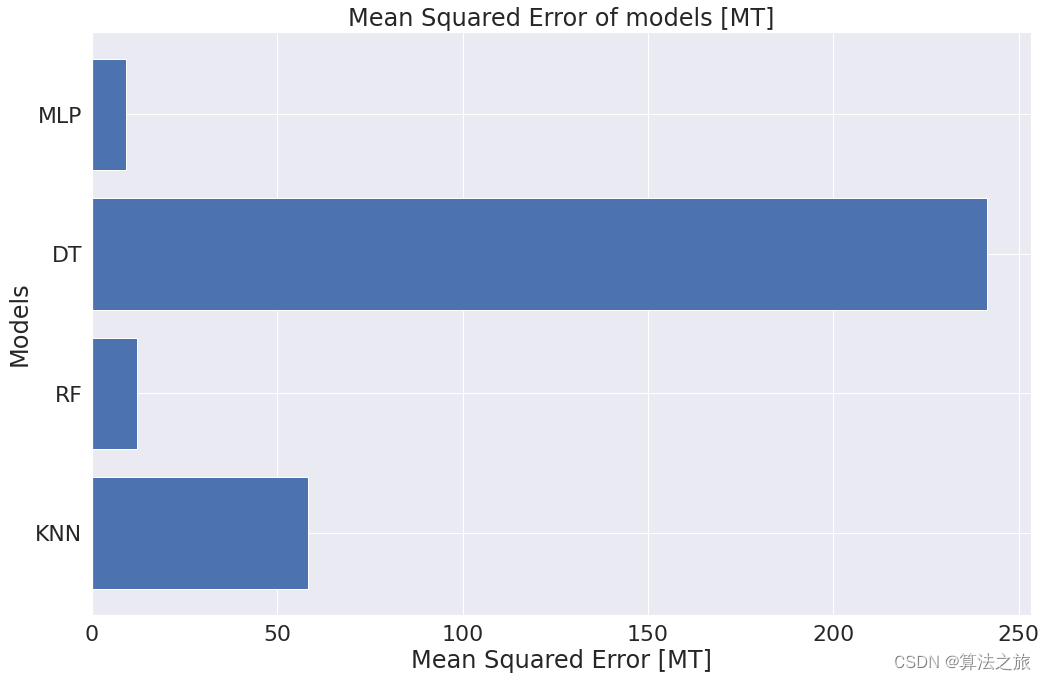
碳排放预测模型 | Python实现基于机器学习回归分析的碳排放预测模型——随机森林、决策树、KNN 和多层感知器 (MLP) 预测分析
文章目录 效果一览文章概述研究内容环境准备源码设计KNNRandom ForestDecision TreeMLPModel Evaluation学习总结参考资料效果一览...

人体检测技术之毫米波雷达
人体检测技术之毫米波雷达 1.概述 智能人脸/视频锁领域的人体检测需求是要求远距离达到1m左右即可,一旦在此距离内检测人,则锁唤醒进行人脸识别,视频录制等操作。所以,人体检测技术非常关键。 选型主要是几个维度: 1.支持检测的距离范围,能否准确输出距离信息 2.支持…...

“Chain of Thought Reasoning“ 和 “Chain Prompts“ 是什么
"Chain of Thought Reasoning" 和 "Chain Prompts" 是什么 1. "Chain Prompts" 是什么2. “Chain of Thought Reasoning” 是什么 1. “Chain Prompts” 是什么 “Chain Prompts” 是指一系列相关的提示,它们之间有逻辑上的联系和依赖关系。用户…...

signal
读信号,dqs 是对齐到dq的边沿, 写信号,dqs 的边沿是对到中间的。 spec 就是这样规定的。我们在dq的最中间的采样,肯定是最安全的。 dqs 是对齐到dq的边沿 , 在silicon 内部,还是通过移位完成的。 rl: re…...

深度研究微软的资产负债表和财务状况以及未来投资价值
来源:猛兽财经 作者:猛兽财经 微软股票的关键指标 猛兽财经认为,微软公布的2023财年第三季度财务业绩,有三个关键指标值得投资者关注。 第一个关键指标是利息收入。微软的利息收入目前已经同比增长了44%,从2022财年第…...
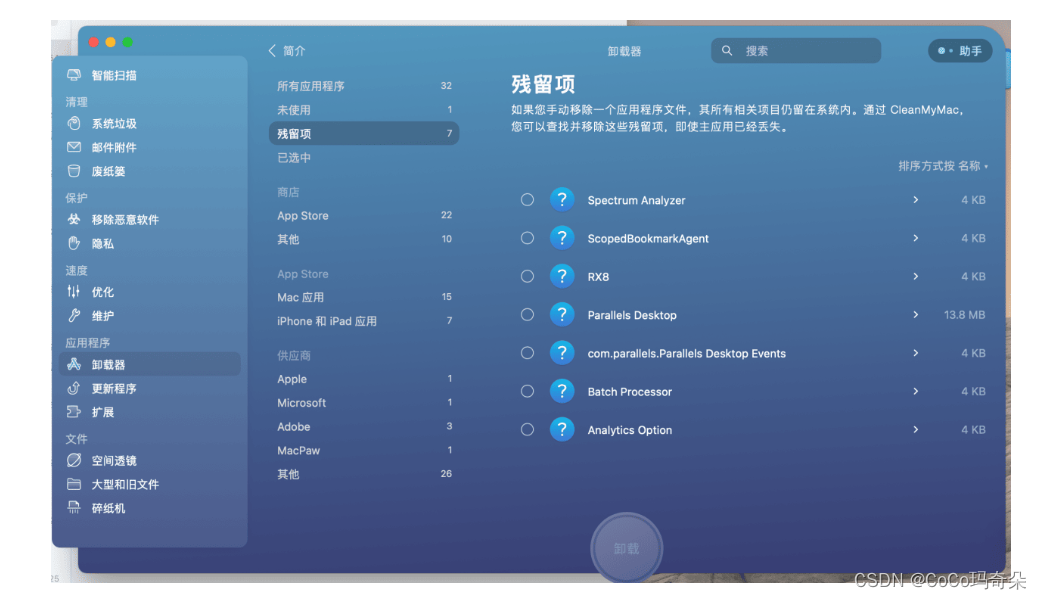
Mac电脑删除第三方软件工具CleanMyMac X
经常使用Mac的人都知道,Mac除了可以在AppStore下载应用程序,还有许多软件是需要在网页上搜索下载的第三方软件。那么这类第三方软件软件除了下载方式不同之外还有什么是和从App store下载的软件有区别的吗?答案是肯定的,那就是这些…...
leetcode174. 地下城游戏(java)
地下城游戏 leetcode174. 地下城游戏题目描述 动态规划解题思路代码 动态规划专题 leetcode174. 地下城游戏 来源:力扣(LeetCode) 链接:https://leetcode.cn/problems/dungeon-game 题目描述 恶魔们抓住了公主并将她关在了地下城 …...

信号与系统复习笔记——傅里叶变换
信号与系统复习笔记——傅里叶变换 周期信号的傅里叶级数表示 特征函数 假设LTI系统的输入为 x ( t ) e s t x(t) e^{st} x(t)est 输出为: y ( t ) e s t ∗ h ( t ) ∫ − ∞ ∞ e s ( t − τ ) h ( τ ) d τ e s t ∫ − ∞ ∞ e − s τ h ( τ ) d…...
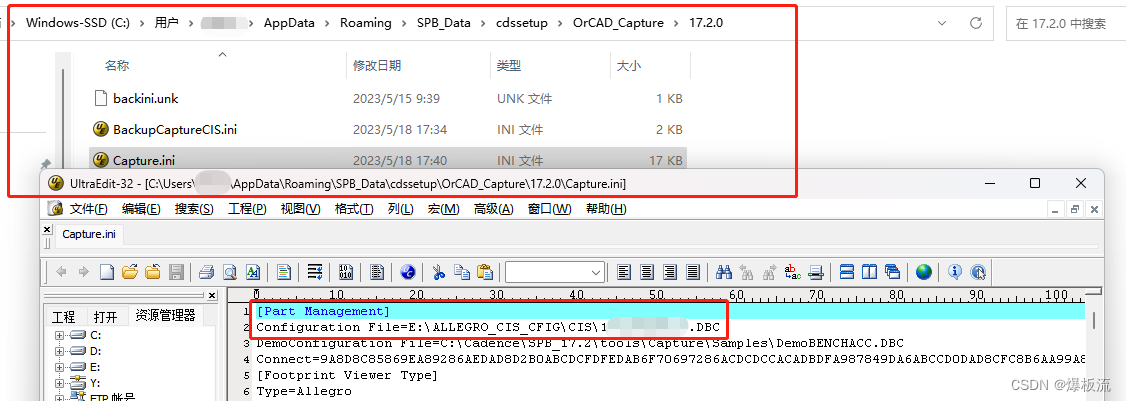
Allegor17.2版本WIN11系统CIS配置提示错误解决方案
错误提示: ERROR(ORCIS-6250): Unable to continue. Database access failed. Contact the database administrator to correct the following error(s), and then retry. ODBC Error Code: -1 Description: 在指定的 DSN 中,驱动程序和应用程序之间的体…...

Java设计模式七大原则-合成聚合复用原则
🧑💻作者:猫十二懿 ❤️🔥账号:CSDN 、掘金 、个人博客 、Github 🎉公众号:猫十二懿 合成-聚合复用原则 1、合成-聚合复用原则介绍 合成/聚合复用原则(Composition/Aggregatio…...

SOFA Weekly|可信基础设施技术分论坛、Layotto 社区会议回顾与预告、社区本周贡献...
SOFA WEEKLY | 每周精选 筛选每周精华问答,同步开源进展 欢迎留言互动~ SOFAStack(Scalable Open Financial Architecture Stack)是蚂蚁集团自主研发的金融级云原生架构,包含了构建金融级云原生架构所需的各个组件&am…...

Melody 监控(四十九)
当新的世界出现,请立即向他奔去 上一章简单介绍了Spring Boot Actuator详解(四十八), 如果没有看过,请观看上一章 一. JavaMelody 一.一 什么是 Java Melody JavaMelody是一个方便的Java或JavaEE Web 应用程序监控工具。 它允许自动存储由 Web 应用程序的实际操…...

Shell脚本管道符常用搭配命令
1.sort sort命令——以行为单位对文件内容进行排序,也可以根据不同的数据类型来排序比较原则是从首字符向后,依次按ASCII码值进行比较,最后将他们按升序输出。 sort [选项] 文件名 cat file | sort [选项] 常用选项 选项作用-n按照数字进行…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...
