信号与系统复习笔记——傅里叶变换
信号与系统复习笔记——傅里叶变换
周期信号的傅里叶级数表示
特征函数
假设LTI系统的输入为 x ( t ) = e s t x(t) = e^{st} x(t)=est 输出为:
y ( t ) = e s t ∗ h ( t ) = ∫ − ∞ + ∞ e s ( t − τ ) h ( τ ) d τ = e s t ∫ − ∞ + ∞ e − s τ h ( τ ) d τ = x ( t ) H ( s ) y(t) = e^{st} \ast h(t) = \int_{-\infty}^{+\infty} e^{s(t - \tau)} h(\tau) d\tau = e^{st}\int_{-\infty}^{+\infty}e^{-s\tau}h(\tau) d\tau = x(t)H(s) y(t)=est∗h(t)=∫−∞+∞es(t−τ)h(τ)dτ=est∫−∞+∞e−sτh(τ)dτ=x(t)H(s)
定义LTI系统的特征函数为:
H ( s ) = ∫ − ∞ + ∞ e − s τ h ( τ ) d τ H(s) = \int_{-\infty}^{+\infty}e^{-s\tau}h(\tau) d\tau H(s)=∫−∞+∞e−sτh(τ)dτ
CT周期函数的傅里叶级数表示
对于周期函数 x T ( t ) x_T(t) xT(t) 来说,周期为 T T T ,角频率为 ω 0 = 2 π T \omega_0 = \frac{2 \pi}{T} ω0=T2π ,那么其傅里叶级数表示的形式为:
x T ( t ) = ∑ k = − ∞ + ∞ a k e j k ω 0 t , (综合公式) x_T(t) = \sum_{k = -\infty}^{+\infty} a_k e^{jk\omega_0t} ,\text{(综合公式)} xT(t)=k=−∞∑+∞akejkω0t,(综合公式)
其中 a k a_k ak 为 x T ( t ) x_T(t) xT(t) 的 k k k 次谐波的傅里叶级数的系数。
其中 e j k ω 0 t e^{jk\omega_0t} ejkω0t 称为旋转因子,而 e − j k ω 0 t e^{-jk\omega_0t} e−jkω0t 称为筛选因子,确定傅里叶系数的方法是两边同时乘以系数为 n n n 的筛选因子:
x T ( t ) e − j n ω 0 t = ∑ k = − ∞ + ∞ a k e j k ω 0 t e − j n ω 0 t x_T(t) e^{-jn\omega_0t} = \sum_{k = -\infty}^{+\infty} a_k e^{jk\omega_0t} e^{-jn\omega_0t} xT(t)e−jnω0t=k=−∞∑+∞akejkω0te−jnω0t
同时在一个周期内做积分:
∫ 0 T x T ( t ) e − j n ω 0 t d t = ∫ 0 T ∑ k = − ∞ + ∞ a k e j k ω 0 t e − j n ω 0 t d t = ∑ k = − ∞ + ∞ a k ∫ 0 T e j ( k − n ) ω 0 t d t \int_0^T x_T(t) e^{-jn\omega_0t} dt = \int_0^T \sum_{k = -\infty}^{+\infty} a_k e^{jk\omega_0t} e^{-jn\omega_0t} dt = \sum_{k = -\infty}^{+\infty} a_k \int_0^T e^{j(k-n)\omega_0t} dt ∫0TxT(t)e−jnω0tdt=∫0Tk=−∞∑+∞akejkω0te−jnω0tdt=k=−∞∑+∞ak∫0Tej(k−n)ω0tdt
对于积分 ∫ 0 T e j ( k − n ) ω 0 t d t \int_0^T e^{j(k-n)\omega_0t} dt ∫0Tej(k−n)ω0tdt 来说,当 k = n k = n k=n 的时候,积分值为 T T T ,否则等于 0 0 0 ,也就是:
∫ 0 T x T ( t ) e − j n ω 0 t d t = T a n \int_0^T x_T(t) e^{-jn\omega_0t} dt = Ta_n ∫0TxT(t)e−jnω0tdt=Tan
即:
a n = 1 T ∫ 0 T x T ( t ) e − j n ω 0 t d t , (分析公式) a_n = \frac{1}{T} \int_0^T x_T(t) e^{-jn\omega_0t} dt,\text{(分析公式)} an=T1∫0TxT(t)e−jnω0tdt,(分析公式)
CT的傅里叶级数的性质
| 性质 | 周期信号 | 傅里叶系数 |
|---|---|---|
| 线性 | A x ( t ) + B y ( t ) Ax(t) +By(t) Ax(t)+By(t) | A a k + B b k Aa_k + Bb_k Aak+Bbk |
| 时移 | x ( t − t 0 ) x(t - t_0) x(t−t0) | a k e − j k ω 0 t 0 a_k e^{-jk\omega_0t_0} ake−jkω0t0 |
| 频移 | x ( t ) e j M ω 0 t x(t)e^{jM\omega_0t} x(t)ejMω0t | a k − M a_{k - M} ak−M |
| 共轭 | x ∗ ( t ) x^*(t) x∗(t) | a − k ∗ a^*_{-k} a−k∗ |
| 时间翻转 | x ( − t ) x(-t) x(−t) | a − k a_{-k} a−k |
| 时域尺度变换 | x ( α t ) x(\alpha t) x(αt) | a k ( T = T / α ) a_k(T=T/\alpha) ak(T=T/α) |
| 周期卷积 | ∫ T x ( τ ) y ( t − τ ) d τ \int_T x(\tau)y(t-\tau) d\tau ∫Tx(τ)y(t−τ)dτ | T a k b k Ta_kb_k Takbk |
| 相乘 | x ( t ) y ( t ) x(t)y(t) x(t)y(t) | ∑ l = − ∞ + ∞ a l b k − l \sum_{l = -\infty}^{+\infty}a_l b_{k-l} ∑l=−∞+∞albk−l |
| 微分 | d x ( t ) d t \frac{dx(t)}{dt} dtdx(t) | j k ω 0 a k jk\omega_0a_k jkω0ak |
| 积分 | ∫ − ∞ t x ( t ) d t \int_{-\infty}^t x(t) dt ∫−∞tx(t)dt | 1 j k ω 0 a k \frac{1}{jk\omega_0}a_k jkω01ak |
| 实信号的共轭对称性 | x ( t ) x(t) x(t) 为实信号 | a k = − a k ∗ a_k = -a^*_k ak=−ak∗ |
| 实偶信号 | x ( t ) x(t) x(t) 为实偶信号 | a k a_k ak 为实偶函数 |
| 实奇信号 | x ( t ) x(t) x(t) 为实奇信号 | a k a_k ak 为纯虚奇函数 |
| 实信号的奇偶分解 | x e ( t ) = E v { x ( t ) } , x o ( t ) = O d { x ( t ) } x_e(t) = Ev\{x(t)\}, x_o(t) = Od\{x(t)\} xe(t)=Ev{x(t)},xo(t)=Od{x(t)} 并且 x ( t ) x(t) x(t) 为实信号 | ℜ { a k } , j ℑ { a k } \Re\{a_k\},j\Im\{a_k\} ℜ{ak},jℑ{ak} |
| 周期信号的帕瓦尔定理 | x ( t ) x(t) x(t) | 1 T ∫ T ∣ x ( t ) ∣ 2 d t = ∑ k = − ∞ + ∞ ∣ a k ∣ 2 \frac{1}{T} \int_T |x(t)|^2 dt = \sum_{k = -\infty}^{+\infty} |a_k|^2 T1∫T∣x(t)∣2dt=∑k=−∞+∞∣ak∣2 |
DT周期信号的傅里叶级数表示
定义周期信号的周期为 N N N ,有 x [ n ] = x [ n + N ] x[n] = x[n + N] x[n]=x[n+N] 。而 ω 0 = 2 π N \omega_0 = \frac{2\pi}{N} ω0=N2π 为基波频率。则 k k k 次谐波转子为:
ϕ k [ n ] = e j k ω 0 n \phi_k[n] = e^{jk\omega_0n} ϕk[n]=ejkω0n
并且,因为再离散时间中, k k k 和 n n n 均为整数的话,那么 ϕ k [ n ] \phi_k[n] ϕk[n] 也为关于 k k k 周期为 N N N 的函数,也就是:
ϕ [ n ] = ϕ k + r N [ n ] \phi[n] = \phi_{k + rN}[n] ϕ[n]=ϕk+rN[n]
这就是说,周期为 N N N 的离散时间信号,其傅里叶级数的系数只有 N N N 个,并且是一个周期为 N N N 的序列。因此DT周期信号的傅里叶级数表示为:
x [ n ] = ∑ k = < N > a k e j k ω o n , (综合公式) x[n] = \sum_{k = <N>} a_k e^{jk\omega_on},\text{(综合公式)} x[n]=k=<N>∑akejkωon,(综合公式)
对于连续的 N N N 个取值:
x [ 0 ] = ∑ k = < N > a k , x [ 1 ] = ∑ k = < N > a k e j k ω 0 , … , x [ N − 1 ] = ∑ k = < N > a k e j k ω 0 ( N − 1 ) x[0] = \sum_{k=<N>} a_k, x[1] = \sum_{k=<N>} a_k e^{jk\omega_0},\ldots, x[N-1] = \sum_{k=<N>} a_k e^{jk\omega_0(N-1)} x[0]=k=<N>∑ak,x[1]=k=<N>∑akejkω0,…,x[N−1]=k=<N>∑akejkω0(N−1)
这些是 N N N 个线性独立的方程,可以直接解出 N N N 个系数的值。若想通过CT同样的方法,有以下的事实:
∑ n = < N > e j k ω 0 n = N ( k = 0 , ± N , ± 2 N , … ) \sum_{n = <N>} e^{jk\omega_0}n = N (k = 0,\pm N,\pm 2N,\ldots) n=<N>∑ejkω0n=N(k=0,±N,±2N,…)
否则其他情况下等于 0 0 0 。
那么同样的,先乘以关于 r r r 的提取因子,然后在一个周期中求和:
∑ n = < N > x [ n ] e − j r ω 0 n = ∑ n = < N > ∑ k = < N > a k e j ( k − r ) ω 0 n = ∑ k = < N > a k ∑ n = < N > e j ( k − r ) ω 0 n \sum_{n = <N>} x[n]e^{-jr\omega_0 n} = \sum_{n = <N>} \sum_{k = <N>} a_k e^{j(k - r)\omega_0 n} = \sum_{k = <N>} a_k \sum_{n = <N>} e^{j(k - r)\omega_0 n} n=<N>∑x[n]e−jrω0n=n=<N>∑k=<N>∑akej(k−r)ω0n=k=<N>∑akn=<N>∑ej(k−r)ω0n
对于和式 ∑ n = < N > e j ( k − r ) ω 0 n \sum_{n = <N>} e^{j(k - r)\omega_0 n} ∑n=<N>ej(k−r)ω0n 当 k = r + c N k = r + cN k=r+cN 的时候,即 k − r k-r k−r 是 N N N 的整数倍的时候,又因为在一个周期内只有一次 k − r k-r k−r 是 N N N 的整数倍,且对应 k = r k = r k=r ,于是右边就等于 N a r Na_r Nar ,因此:
a r = 1 N ∑ n = < N > x [ n ] e − j r ω 0 n , (分析公式) a_r = \frac{1}{N} \sum_{n = <N>} x[n]e^{-jr\omega_0 n},\text{(分析公式)} ar=N1n=<N>∑x[n]e−jrω0n,(分析公式)
DT的傅里叶级数的性质
| 性质 | 周期信号 | 傅里叶系数 |
|---|---|---|
| 线性 | A x [ n ] + B y [ n ] Ax[n] +By[n] Ax[n]+By[n] | A a k + B b k Aa_k + Bb_k Aak+Bbk |
| 时移 | x [ n − n 0 ] x[n - n_0] x[n−n0] | a k e − j k ω 0 n 0 a_k e^{-jk\omega_0n_0} ake−jkω0n0 |
| 频移 | x [ n ] e j M ω 0 n x[n]e^{jM\omega_0n} x[n]ejMω0n | a k − M a_{k - M} ak−M |
| 共轭 | x ∗ [ n ] x^*[n] x∗[n] | a − k ∗ a^*_{-k} a−k∗ |
| 时间翻转 | x [ − n ] x[-n] x[−n] | a − k a_{-k} a−k |
| 时域尺度变换 | x ( m ) [ n ] = x [ n / m ] x_{(m)}[n]=x[n/m] x(m)[n]=x[n/m] | 1 m a k ( N = N m ) \frac{1}{m}a_k(N=Nm) m1ak(N=Nm) |
| 周期卷积 | ∑ r = < N > x [ r ] y [ n − r ] d τ \sum_{r = <N>} x[r]y[n-r] d\tau ∑r=<N>x[r]y[n−r]dτ | N a k b k Na_kb_k Nakbk |
| 相乘 | x [ n ] y [ n ] x[n]y[n] x[n]y[n] | ∑ l = < N > a l b k − l \sum_{l = <N>} a_l b_{k-l} ∑l=<N>albk−l |
| 一阶差分 | x [ n ] − x [ n − 1 ] x[n] - x[n - 1] x[n]−x[n−1] | ( 1 − e − j k ω 0 ) a k (1 - e^{-jk\omega_0})a_k (1−e−jkω0)ak |
| 求和 | ∑ k = − ∞ n x [ k ] \sum_{k = -\infty}^{n} x[k] ∑k=−∞nx[k] | 1 ( 1 − e − j k ω 0 ) a k \frac{1}{(1 - e^{-jk\omega_0})}a_k (1−e−jkω0)1ak |
| 实信号的共轭对称性 | x [ n ] x[n] x[n] 为实信号 | a k = − a k ∗ a_k = -a^*_k ak=−ak∗ |
| 实偶信号 | x [ n ] x[n] x[n] 为实偶信号 | a k a_k ak 为实偶函数 |
| 实奇信号 | x [ n ] x[n] x[n] 为实奇信号 | a k a_k ak 为纯虚奇函数 |
| 实信号的奇偶分解 | x e [ n ] = E v { x [ n ] } , x o [ n ] = O d { x [ n ] } x_e[n] = Ev\{x[n]\}, x_o[n] = Od\{x[n]\} xe[n]=Ev{x[n]},xo[n]=Od{x[n]} 并且 x [ n ] x[n] x[n] 为实信号 | ℜ { a k } , j ℑ { a k } \Re\{a_k\},j\Im\{a_k\} ℜ{ak},jℑ{ak} |
| 周期信号的帕瓦尔定理 | x [ n ] x[n] x[n] | 1 N ∑ n = < N > ∣ x [ n ] ∣ 2 = ∑ k = < N > ∣ a k ∣ 2 \frac{1}{N} \sum_{n = <N>} |x[n]|^2 = \sum_{k = <N>} |a_k|^2 N1∑n=<N>∣x[n]∣2=∑k=<N>∣ak∣2 |
连续时间傅里叶变换
连续时间非周期的傅里叶表示
假设连续时间的周期信号为 x T ( t ) x_T(t) xT(t) ,对应的单个周期信号为 x ( t ) x(t) x(t) ,因为:
a k = 1 T ∫ − T / 2 T / 2 x T ( t ) e − j k ω 0 t d t = 1 T ∫ − ∞ + ∞ x ( t ) e − j k ω 0 t d t a_k = \frac{1}{T} \int_{-T/2}^{T/2} x_T(t) e^{-jk\omega_0t} dt = \frac{1}{T} \int_{-\infty}^{+\infty} x(t) e^{-jk\omega_0t} dt ak=T1∫−T/2T/2xT(t)e−jkω0tdt=T1∫−∞+∞x(t)e−jkω0tdt
定义 T a k Ta_k Tak 的包络函数为:
X ( j ω ) = ∫ − ∞ + ∞ x ( t ) e − j ω t d t , (分析公式) X(j\omega) = \int_{-\infty}^{+\infty} x(t) e^{-j\omega t} dt,\text{(分析公式)} X(jω)=∫−∞+∞x(t)e−jωtdt,(分析公式)
此时 a k a_k ak 可以表示为:
a k = 1 T X ( j k ω 0 ) a_k = \frac{1}{T} X(jk\omega_0) ak=T1X(jkω0)
并且:
x T ( t ) = ∑ k = − ∞ + ∞ 1 T X ( j k ω 0 ) e j k ω 0 t = 1 2 π ∑ k = − ∞ + ∞ X ( j k ω 0 ) e j k ω 0 t ω 0 x_T(t) = \sum_{k = -\infty}^{+\infty} \frac{1}{T}X(jk\omega_0) e^{jk\omega_0t} = \frac{1}{2\pi} \sum_{k = -\infty}^{+\infty} X(jk\omega_0) e^{jk\omega_0t} \omega_0 xT(t)=k=−∞∑+∞T1X(jkω0)ejkω0t=2π1k=−∞∑+∞X(jkω0)ejkω0tω0
接下来进行周期延拓,即 lim T → ∞ x T ( t ) = x ( t ) \lim_{T \to \infty} x_T(t) = x(t) limT→∞xT(t)=x(t) 有:
x ( t ) = 1 2 π ∫ − ∞ + ∞ X ( j ω ) e j ω t d ω , (综合公式) x(t) = \frac{1}{2\pi} \int_{-\infty}^{+\infty} X(j\omega) e^{j\omega t} d\omega,\text{(综合公式)} x(t)=2π1∫−∞+∞X(jω)ejωtdω,(综合公式)
上面两式称为傅里叶变换。
连续时间傅里叶变换的性质
| 性质 | 周期信号 | 傅里叶系数 |
|---|---|---|
| 线性 | A x ( t ) + B y ( t ) Ax(t) +By(t) Ax(t)+By(t) | A X ( j ω ) + B Y ( j ω ) AX(j\omega) + BY(j\omega) AX(jω)+BY(jω) |
| 时移 | x ( t − t 0 ) x(t - t_0) x(t−t0) | X ( j ω ) e − j ω t 0 X(j\omega) e^{-j\omega t_0} X(jω)e−jωt0 |
| 频移 | x ( t ) e j ω 0 t x(t)e^{j\omega_0 t} x(t)ejω0t | X ( j ( ω − ω 0 ) ) X(j(\omega - \omega_0)) X(j(ω−ω0)) |
| 共轭 | x ∗ ( t ) x^*(t) x∗(t) | X ∗ ( − j ω ) X^*(-j\omega) X∗(−jω) |
| 时间翻转 | x ( − t ) x(-t) x(−t) | X ( − j ω ) X(-j\omega) X(−jω) |
| 时域尺度变换 | x ( α t ) x(\alpha t) x(αt) | 1 ∣ a ∣ X ( j ω a ) \frac{1}{|a|} X(\frac{j\omega}{a}) ∣a∣1X(ajω) |
| 卷积 | x ( t ) ∗ y ( t ) x(t) \ast y(t) x(t)∗y(t) | X ( j ω ) Y ( j ω ) X(j\omega)Y(j\omega) X(jω)Y(jω) |
| 相乘 | x ( t ) y ( t ) x(t)y(t) x(t)y(t) | 1 2 π ∫ − ∞ + ∞ X ( j θ ) Y ( j ( ω − θ ) ) d θ \frac{1}{2\pi}\int_{-\infty}^{+\infty}X(j\theta) Y(j(\omega - \theta)) d\theta 2π1∫−∞+∞X(jθ)Y(j(ω−θ))dθ |
| 时域微分 | d x ( t ) d t \frac{dx(t)}{dt} dtdx(t) | j ω X ( j ω ) j\omega X(j\omega) jωX(jω) |
| 时域积分 | ∫ − ∞ t x ( t ) d t \int_{-\infty}^t x(t) dt ∫−∞tx(t)dt | 1 j ω X ( j ω ) + π X ( 0 ) δ ( ω ) \frac{1}{j\omega} X(j\omega) + \pi X(0)\delta(\omega) jω1X(jω)+πX(0)δ(ω) |
| 频域微分 | t x ( t ) tx(t) tx(t) | j d d ω X ( j ω ) j\frac{d}{d\omega}X(j\omega) jdωdX(jω) |
| 实信号的共轭对称性 | x ( t ) x(t) x(t) 为实信号 | X ( j ω ) = X ∗ ( − j ω ) X(j\omega) = X^*(-j\omega) X(jω)=X∗(−jω) |
| 实偶信号 | x ( t ) x(t) x(t) 为实偶信号 | X ( j ω ) X(j\omega) X(jω) 为实偶函数 |
| 实奇信号 | x ( t ) x(t) x(t) 为实奇信号 | X ( j ω ) X(j\omega) X(jω) 为纯虚奇函数 |
| 实信号的奇偶分解 | x e ( t ) = E v { x ( t ) } , x o ( t ) = O d { x ( t ) } x_e(t) = Ev\{x(t)\}, x_o(t) = Od\{x(t)\} xe(t)=Ev{x(t)},xo(t)=Od{x(t)} 并且 x ( t ) x(t) x(t) 为实信号 | ℜ { X ( j ω ) } , j ℑ { X ( j ω ) } \Re\{X(j\omega)\},j\Im\{X(j\omega)\} ℜ{X(jω)},jℑ{X(jω)} |
| 周期信号的帕瓦尔定理 | x ( t ) x(t) x(t) | ∫ − ∞ + ∞ ∣ x ( t ) ∣ 2 d t = 1 2 π ∫ − ∞ + ∞ ∣ X ( j ω ) ∣ 2 d ω \int_{-\infty}^{+\infty} |x(t)|^2 dt = \frac{1}{2\pi} \int_{-\infty}^{+\infty} |X(j\omega)|^2 d\omega ∫−∞+∞∣x(t)∣2dt=2π1∫−∞+∞∣X(jω)∣2dω |
基本傅里叶变换对
- 周期信号的傅里叶变换
考虑这样一个信号的傅里叶变换为:
X ( j ω ) = 2 π δ ( ω − ω 0 ) X(j\omega) = 2\pi\delta(\omega - \omega_0) X(jω)=2πδ(ω−ω0)
其对应的时域信号为:
x ( t ) = 1 2 π ∫ − ∞ + ∞ 2 π δ ( ω − ω 0 ) e j ω t d ω = e j ω 0 t x(t) = \frac{1}{2 \pi} \int_{-\infty}^{+\infty} 2\pi \delta(\omega - \omega_0) e^{j\omega t} d\omega = e^{j\omega_0 t} x(t)=2π1∫−∞+∞2πδ(ω−ω0)ejωtdω=ejω0t
那么通过周期信号的傅里叶系数关系为:
X ( j ω ) = ∑ k = − ∞ + ∞ 2 π a k δ ( ω − k ω 0 ) X(j\omega) = \sum_{k = -\infty}^{+\infty} 2 \pi a_k \delta(\omega - k\omega_0) X(jω)=k=−∞∑+∞2πakδ(ω−kω0)
其对应的时域信号为:
x ( t ) = ∑ k = − ∞ + ∞ a k e j k ω 0 t x(t) = \sum_{k = -\infty}^{+\infty} a_k e^{jk\omega_0 t} x(t)=k=−∞∑+∞akejkω0t
- 单边衰减信号
考虑信号 x ( t ) = e − a t u ( t ) , a > 0 x(t) = e^{-at}u(t), a> 0 x(t)=e−atu(t),a>0 。其对应的傅里叶变换为:
X ( j ω ) = ∫ 0 ∞ e − a t e − j ω t d t = − 1 a + j ω e − ( a + j ω ) t ∣ 0 ∞ = 1 a + j ω ( a > 0 ) X(j\omega) = \int_0^{\infty} e^{-at} e^{-j\omega t} dt = -\frac{1}{a + j\omega} e^{-(a + j\omega)t} |_0^\infty = \frac{1}{a + j\omega} (a>0) X(jω)=∫0∞e−ate−jωtdt=−a+jω1e−(a+jω)t∣0∞=a+jω1(a>0)
- 双边衰减信号
考虑信号 x ( t ) = e − a ∣ t ∣ , a > 0 x(t) = e^{-a|t|}, a> 0 x(t)=e−a∣t∣,a>0 。其对应的傅里叶变换为:
X ( j ω ) = 1 a − j ω + 1 a + j ω = 2 a a 2 + ω 2 X(j\omega) = \frac{1}{a - j\omega} + \frac{1}{a + j\omega} = \frac{2a}{a^2 + \omega^2} X(jω)=a−jω1+a+jω1=a2+ω22a
- 单位冲激函数的傅里叶变换
单位冲激函数 x ( t ) = δ ( t ) x(t) = \delta(t) x(t)=δ(t) 的傅里叶变换为:
X ( j ω ) = ∫ − ∞ + ∞ δ ( t ) e − j ω t d t = 1 X(j\omega) = \int_{-\infty}^{+\infty} \delta(t) e^{-j\omega t} dt = 1 X(jω)=∫−∞+∞δ(t)e−jωtdt=1
- 矩形脉冲信号的傅里叶变换
考虑一个矩形脉冲信号:
x ( t ) = 1 , ∣ t ∣ < T 1 x(t) = 1 ,|t| < T_1 x(t)=1,∣t∣<T1
x ( t ) = 0 , ∣ t ∣ > T 1 x(t) = 0 ,|t| > T_1 x(t)=0,∣t∣>T1
其傅里叶变换为:
X ( j ω ) = ∫ − T 1 T 1 e j ω t d t = 2 sin ω T 1 ω X(j\omega) = \int_{-T_1}^{T_1} e^{j\omega t} dt = 2\frac{\sin \omega T_1}{\omega} X(jω)=∫−T1T1ejωtdt=2ωsinωT1
- 傅里叶变换的对偶性
假设信号 x ( t ) x(t) x(t) 存在傅里叶变换对:
X ( j ω ) = ∫ − ∞ + ∞ x ( t ) e − j ω t d t X(j\omega) = \int_{-\infty}^{+\infty} x(t) e^{-j\omega t} dt X(jω)=∫−∞+∞x(t)e−jωtdt
x ( t ) = 1 2 π ∫ − ∞ + ∞ X ( j ω ) e j ω t d ω x(t) = \frac{1}{2 \pi} \int_{-\infty}^{+\infty} X(j\omega) e^{j\omega t} d\omega x(t)=2π1∫−∞+∞X(jω)ejωtdω
那么信号 X ( j t ) X(jt) X(jt) 存在傅里叶变换对:
∫ − ∞ + ∞ X ( j t ) e − j ω t d t = 2 π x ( − ω ) \int_{-\infty}^{+\infty} X(jt) e^{-j\omega t} dt = 2\pi x(-\omega) ∫−∞+∞X(jt)e−jωtdt=2πx(−ω)
1 2 π ∫ − ∞ + ∞ x ( ω ) e j ω t d ω = 1 2 π X ( − j t ) \frac{1}{2 \pi} \int_{-\infty}^{+\infty} x(\omega) e^{j\omega t} d\omega = \frac{1}{2 \pi} X(-jt) 2π1∫−∞+∞x(ω)ejωtdω=2π1X(−jt)
- 典型的傅里叶变换对
| 信号 | 傅里叶变换 | 傅里叶级数系数(若是周期信号) |
|---|---|---|
| ∑ k = − ∞ + ∞ a k e j k ω 0 t \sum_{k = -\infty}^{+\infty} a_k e^{jk\omega_0 t} ∑k=−∞+∞akejkω0t | ∑ k = − ∞ + ∞ 2 π a k δ ( ω − k ω 0 ) \sum_{k = -\infty}^{+\infty} 2 \pi a_k \delta(\omega - k\omega_0) ∑k=−∞+∞2πakδ(ω−kω0) | a k a_k ak |
| e j k ω 0 t e^{jk\omega_0 t} ejkω0t | 2 π δ ( ω − k ω 0 ) 2\pi \delta(\omega-k\omega_0) 2πδ(ω−kω0) | a 1 = 1 , a k = 0 a_1 = 1,a_k = 0 a1=1,ak=0 |
| cos ω 0 t \cos \omega_0 t cosω0t | π [ δ ( ω − ω 0 ) + δ ( ω + ω 0 ) ] \pi[\delta(\omega - \omega_0) + \delta(\omega + \omega_0)] π[δ(ω−ω0)+δ(ω+ω0)] | a 1 = a − 1 = 1 2 , a k = 0 a_1 = a_{-1} = \frac{1}{2},a_k = 0 a1=a−1=21,ak=0 |
| sin ω 0 t \sin \omega_0 t sinω0t | π j [ δ ( ω − ω 0 ) − δ ( ω + ω 0 ) ] \frac{\pi}{j}[\delta(\omega - \omega_0) - \delta(\omega + \omega_0)] jπ[δ(ω−ω0)−δ(ω+ω0)] | a 1 = − a − 1 = 1 2 j , a k = 0 a_1 = -a_{-1} = \frac{1}{2j},a_k = 0 a1=−a−1=2j1,ak=0 |
| x ( t ) = 1 x(t) = 1 x(t)=1 | 2 π δ ( ω ) 2\pi\delta(\omega) 2πδ(ω) | a 0 = 1 , a k = 0 a_0 = 1,a_k = 0 a0=1,ak=0 |
| 周期方波 x ( t ) = 1 , ∣ t ∣ < T 1 x(t) = 1 ,|t| < T_1 x(t)=1,∣t∣<T1 | ∑ k = − ∞ + ∞ 2 sin k ω 0 T 1 k δ ( ω − k ω 0 ) \sum_{k = -\infty}^{+\infty}\frac{2\sin k\omega_0 T_1}{k}\delta(\omega - k\omega_0) ∑k=−∞+∞k2sinkω0T1δ(ω−kω0) | sin k ω 0 T 1 k π \frac{\sin k\omega_0T_1}{k\pi} kπsinkω0T1 |
| 周期冲激串 ∑ n = − ∞ + ∞ δ ( t − n T ) \sum_{n = -\infty}^{+\infty}\delta(t - nT) ∑n=−∞+∞δ(t−nT) | 2 π T ∑ k = − ∞ + ∞ δ ( ω − 2 π k T ) \frac{2 \pi}{T}\sum_{k = -\infty}^{+\infty}\delta(\omega - \frac{2\pi k}{T}) T2π∑k=−∞+∞δ(ω−T2πk) | a k = 1 T a_k = \frac{1}{T} ak=T1 |
| 矩形阶跃函数 x ( t ) = 1 , ∣ t ∣ < T 1 x(t) = 1,|t| < T_1 x(t)=1,∣t∣<T1 | 2 sin ω T 1 ω \frac{2 \sin \omega T_1}{\omega} ω2sinωT1 | - |
| sin W t π t \frac{\sin Wt}{\pi t} πtsinWt | X ( j ω ) = 1 , ∣ ω ∣ < W X(j\omega) = 1, |\omega| <W X(jω)=1,∣ω∣<W | - |
| δ ( t ) \delta(t) δ(t) | 1 1 1 | - |
| u ( t ) u(t) u(t) | 1 j ω + π δ ( ω ) \frac{1}{j \omega} + \pi \delta(\omega) jω1+πδ(ω) | - |
| δ ( t − t 0 ) \delta(t - t_0) δ(t−t0) | e j ω t 0 e^{j\omega t_0} ejωt0 | - |
| e − a t u ( t ) , ℜ a > 0 e^{-at}u(t),\Re{a} > 0 e−atu(t),ℜa>0 | 1 a + j ω \frac{1}{a+j\omega} a+jω1 | - |
| t e − a t u ( t ) , ℜ a > 0 te^{-at}u(t),\Re{a} > 0 te−atu(t),ℜa>0 | 1 ( a + j ω ) 2 \frac{1}{(a+j\omega)^2} (a+jω)21 | - |
| t n − 1 ( n − 1 ) ! e − a t u ( t ) , ℜ a > 0 \frac{t^{n-1}}{(n-1)!}e^{-at}u(t),\Re{a} > 0 (n−1)!tn−1e−atu(t),ℜa>0 | 1 ( a + j ω ) n \frac{1}{(a+j\omega)^n} (a+jω)n1 | - |
傅里叶变换与线性常系数微分方程表述的系统
对于线性常系数微分方程描述的系统:
∑ k = 0 N a k d k y ( t ) d t k = ∑ k = 0 M b k d k x ( t ) d t k \sum_{k=0}^{N} a_k \frac{d^k y(t)}{dt^k} = \sum_{k=0}^{M} b_k \frac{d^k x(t)}{dt^k} k=0∑Nakdtkdky(t)=k=0∑Mbkdtkdkx(t)
有卷积关系:
y ( t ) = h ( t ) ∗ x ( t ) y(t) = h(t) \ast x(t) y(t)=h(t)∗x(t)
根据傅里叶变换的性质有:
Y ( j ω ) = H ( j ω ) X ( j ω ) Y(j\omega) = H(j \omega) X(j \omega) Y(jω)=H(jω)X(jω)
我们称函数 H ( j ω ) H(j \omega) H(jω) 为 系统频响函数 。
对微分方程两边做傅里叶变换:
F { ∑ k = 0 N a k d k y ( t ) d t k } = F { ∑ k = 0 M b k d k x ( t ) d t k } \mathscr{F} \{\sum_{k=0}^{N} a_k \frac{d^k y(t)}{dt^k}\} = \mathscr{F} \{\sum_{k=0}^{M} b_k \frac{d^k x(t)}{dt^k}\} F{k=0∑Nakdtkdky(t)}=F{k=0∑Mbkdtkdkx(t)}
根据傅里叶变换的微分性质:
∑ k = 0 N a k ( j ω ) k Y ( j ω ) = ∑ k = 0 M b k ( j ω ) k X ( j ω ) \sum_{k=0}^{N} a_k (j\omega)^k Y(j\omega) = \sum_{k=0}^{M} b_k (j\omega)^k X(j\omega) k=0∑Nak(jω)kY(jω)=k=0∑Mbk(jω)kX(jω)
可得:
H ( j ω ) = Y ( j ω ) X ( j ω ) = ∑ k = 0 M b k ( j ω ) k ∑ k = 0 N a k ( j ω ) k H(j\omega) = \frac{Y(j\omega)}{X(j\omega)} = \frac{\sum_{k=0}^{M} b_k (j\omega)^k}{\sum_{k=0}^{N} a_k (j\omega)^k} H(jω)=X(jω)Y(jω)=∑k=0Nak(jω)k∑k=0Mbk(jω)k
离散时间傅里叶变换
离散时间非周期的傅里叶表示
假设有离散时间的信号 x T [ n ] x_T[n] xT[n] ,那么其傅里叶系数表示为:
a k = 1 N ∑ n = < N > x [ n ] e − j k ω 0 n a_k = \frac{1}{N} \sum_{n = <N>} x[n] e^{-jk\omega_0n} ak=N1n=<N>∑x[n]e−jkω0n
其对应的非周期的信号表示在一个周期内 [ − N 1 , N 2 ] [-N_1,N_2] [−N1,N2] 为 x [ n ] x[n] x[n] ,那么:
a k = 1 N ∑ n = − N 1 N 2 x [ n ] e − j k ω 0 n = 1 N ∑ n = − ∞ + ∞ x [ n ] e − j k ω 0 n a_k = \frac{1}{N} \sum_{n = -N_1}^{N_2} x[n] e^{-jk\omega_0n} = \frac{1}{N} \sum_{n = -\infty}^{+\infty} x[n] e^{-jk\omega_0n} ak=N1n=−N1∑N2x[n]e−jkω0n=N1n=−∞∑+∞x[n]e−jkω0n
我们定义 a k N a_kN akN 的包络:
X ( e j ω ) = ∑ n = − ∞ + ∞ x [ n ] e − j ω n , 分析公式 X(e^{j\omega}) = \sum_{n = -\infty}^{+\infty} x[n] e^{-j\omega n},\text{分析公式} X(ejω)=n=−∞∑+∞x[n]e−jωn,分析公式
为离散时间傅里叶变换。
那么有:
a k = 1 N X ( e j k ω 0 ) a_k = \frac{1}{N} X(e^{jk\omega_0}) ak=N1X(ejkω0)
则重新带回原始得到:
x T [ n ] = ∑ k = < N > 1 N X ( e j k ω 0 ) e j k ω 0 n = 1 2 π ∑ k = < N > X ( e j k ω 0 ) e j k ω 0 n ω 0 x_T[n] = \sum_{k = <N>} \frac{1}{N} X(e^{jk\omega_0}) e^{jk\omega_0n} = \frac{1}{2\pi} \sum_{k = <N>}X(e^{jk\omega_0}) e^{jk\omega_0n} \omega_0 xT[n]=k=<N>∑N1X(ejkω0)ejkω0n=2π1k=<N>∑X(ejkω0)ejkω0nω0
当 N → ∞ N \to \infty N→∞ 的时候,其在一个周期上的求和就变成了在 2 π 2\pi 2π 内的一个积分,即:
x [ n ] = 1 2 π ∫ 2 π X ( e j ω ) e j ω n d ω , 综合公式 x[n] = \frac{1}{2\pi} \int_{2 \pi} X(e^{j\omega}) e^{j\omega n} d\omega, \text{综合公式} x[n]=2π1∫2πX(ejω)ejωndω,综合公式
因为 X ( e j ω ) e j ω n X(e^{j\omega}) e^{j\omega n} X(ejω)ejωn 关于 ω \omega ω 周期为 2 π 2\pi 2π 的函数,这说明我们的积分区间可以随意取一个连续的 2 π 2\pi 2π 周期。
同时,对于非周期信号的傅里叶变换频谱公式 X ( e j ω ) X(e^{j\omega}) X(ejω) 来说,也是一个关于 ω \omega ω 周期为 2 π 2\pi 2π 的函数,这说明 非周期的离散信号的傅里叶频谱是一个周期为 2 π 2\pi 2π 的函数 。
离散时间非周期的傅里叶的性质
| 性质 | 周期信号 | 傅里叶系数 |
|---|---|---|
| 线性 | A x [ n ] + B y [ n ] Ax[n] +By[n] Ax[n]+By[n] | A X ( e j ω ) + B Y ( e j ω ) AX(e^{j\omega}) + BY(e^{j\omega}) AX(ejω)+BY(ejω) |
| 时移 | x [ n − n 0 ] x[n - n_0] x[n−n0] | X ( e j ω ) e − j ω n 0 X(e^{j\omega}) e^{-j\omega n_0} X(ejω)e−jωn0 |
| 频移 | x [ n ] e j ω 0 n x[n]e^{j\omega_0 n} x[n]ejω0n | X ( e j ( ω − ω 0 ) ) X(e^{j(\omega - \omega_0)}) X(ej(ω−ω0)) |
| 共轭 | x ∗ [ n ] x^*[n] x∗[n] | X ∗ ( e − j ω ) X^*(e^{-j\omega}) X∗(e−jω) |
| 时间翻转 | x [ − n ] x[-n] x[−n] | X ( e − j ω ) X(e^{-j\omega}) X(e−jω) |
| 时域尺度变换 | x ( k ) [ n ] = x [ n / k ] x_{(k)}[n] = x[n/k] x(k)[n]=x[n/k] | X ( e j k ω ) X(e^{jk\omega}) X(ejkω) |
| 卷积 | x [ n ] ∗ y [ n ] x[n] \ast y[n] x[n]∗y[n] | X ( e j ω ) Y ( e j ω ) X(e^{j\omega})Y(e^{j\omega}) X(ejω)Y(ejω) |
| 相乘 | x [ t ] y [ t ] x[t]y[t] x[t]y[t] | 1 2 π ∫ 2 π X ( e j θ ) Y ( e j ( ω − θ ) ) d θ \frac{1}{2\pi}\int_{2\pi} X(e^{j\theta}) Y(e^{j(\omega - \theta)}) d\theta 2π1∫2πX(ejθ)Y(ej(ω−θ))dθ |
| 时域差分 | x [ n ] − x [ n − 1 ] x[n] - x[n-1] x[n]−x[n−1] | ( 1 − e − j ω ) X ( e j ω ) (1 - e^{-j\omega})X(e^{j\omega}) (1−e−jω)X(ejω) |
| 时域累加 | ∑ k = − ∞ n x [ k ] \sum_{k=-\infty}^n x[k] ∑k=−∞nx[k] | 1 1 − e − j ω X ( e j ω ) + π X ( e j 0 ) ∑ k = − ∞ + ∞ δ ( ω − 2 π k ) \frac{1}{1 - e^{-j\omega}}X(e^{j\omega}) +\pi X(e^{j0})\sum_{k=-\infty}^{+\infty}\delta(\omega - 2\pi k) 1−e−jω1X(ejω)+πX(ej0)∑k=−∞+∞δ(ω−2πk) |
| 频域微分 | n x [ n ] nx[n] nx[n] | j d d ω X ( e j ω ) j\frac{d}{d\omega}X(e^{j\omega}) jdωdX(ejω) |
| 实信号的共轭对称性 | x [ n ] x[n] x[n] 为实信号 | X ( e j ω ) = X ∗ ( e − j ω ) X(e^{j\omega}) = X^*(e^{-j\omega}) X(ejω)=X∗(e−jω) |
| 实偶信号 | x [ n ] x[n] x[n] 为实偶信号 | X ( e j ω ) X(e^{j\omega}) X(ejω) 为实偶函数 |
| 实奇信号 | x [ n ] x[n] x[n] 为实奇信号 | X ( e j ω ) X(e^{j\omega}) X(ejω) 为纯虚奇函数 |
| 实信号的奇偶分解 | x e [ n ] = E v { x [ n ] } , x o [ n ] = O d { x [ n ] } x_e[n] = Ev\{x[n]\}, x_o[n] = Od\{x[n]\} xe[n]=Ev{x[n]},xo[n]=Od{x[n]} 并且 x [ n ] x[n] x[n] 为实信号 | ℜ { X ( e j ω ) } , j ℑ { X ( e j ω ) } \Re\{X(e^{j\omega})\},j\Im\{X(e^{j\omega})\} ℜ{X(ejω)},jℑ{X(ejω)} |
| 周期信号的帕瓦尔定理 | x [ n ] x[n] x[n] | ∑ n = − ∞ + ∞ ∣ x [ n ] ∣ 2 = 1 2 π ∫ 2 π ∣ X ( e j ω ) ∣ 2 d ω \sum_{n = -\infty}^{+\infty} |x[n]|^2 = \frac{1}{2\pi} \int_{2\pi} |X(e^{j\omega})|^2 d\omega ∑n=−∞+∞∣x[n]∣2=2π1∫2π∣X(ejω)∣2dω |
基本离散时间信号的傅里叶变换对
- 周期信号
考虑信号 x [ n ] = e j ω 0 n x[n] = e^{j\omega_0 n} x[n]=ejω0n 的傅里变换为:
X ( e j ω ) = ∑ l = − ∞ + ∞ 2 π δ ( ω − ω 0 − 2 π l ) X(e^{j\omega}) = \sum_{l = -\infty}^{+\infty} 2\pi \delta(\omega - \omega_0 - 2\pi l) X(ejω)=l=−∞∑+∞2πδ(ω−ω0−2πl)
现在考虑一个周期为 N N N 的周期序列,其傅里叶级数为:
x [ n ] = ∑ k = < N > a k e j k ω 0 n x[n] = \sum_{k = <N>} a_k e^{jk\omega_0 n} x[n]=k=<N>∑akejkω0n
那么他的傅里叶变换就是:
X ( e j ω ) = ∑ k = − ∞ + ∞ 2 π a k δ ( ω − 2 π k N ) X(e^{j\omega}) = \sum_{k = -\infty}^{+\infty} 2 \pi a_k \delta(\omega - \frac{2\pi k}{N}) X(ejω)=k=−∞∑+∞2πakδ(ω−N2πk)
- 离散时间傅里叶系数的对偶性
若两个周期为 N N N 的序列 f [ n ] f[n] f[n] 和 g [ n ] g[n] g[n] ,若 f [ k ] f[k] f[k] 是 g [ n ] g[n] g[n] 的离散时间傅里叶系数,即
g [ n ] ↔ f [ k ] g[n] \leftrightarrow f[k] g[n]↔f[k]
那么:
f [ n ] ↔ 1 N g [ − k ] f[n] \leftrightarrow \frac{1}{N}g[-k] f[n]↔N1g[−k]
- 离散时间傅里叶变换和连续时间傅里叶系数的对偶性
考虑离散时间傅里叶变换:
X ( e j ω ) = ∑ n = − ∞ + ∞ x [ n ] e − j ω n X(e^{j\omega}) = \sum_{n = -\infty}^{+\infty} x[n] e^{-j\omega n} X(ejω)=n=−∞∑+∞x[n]e−jωn
与连续时间傅里叶系数:
x ( t ) = ∑ k = − ∞ + ∞ a k e − j k ω 0 t x(t) = \sum_{k = -\infty}^{+\infty} a_k e^{-jk\omega_0 t} x(t)=k=−∞∑+∞ake−jkω0t
这相当于将 x [ n ] x[n] x[n] 看成是一个连续时间函数的傅里叶系数,同理,我们可以将 x ( t ) x(t) x(t) 看做是一个离散时间函数的傅里叶变换。
- 常用基本离散时间信号的傅里叶变换对表
| 信号 | 傅里叶变换 | 傅里叶系数(若为周期的) |
|---|---|---|
| ∑ k = < N > a k e j k ω 0 n , N = 2 π ω 0 \sum_{k = <N>}a_k e^{jk\omega_0 n},N = \frac{2\pi}{\omega_0} ∑k=<N>akejkω0n,N=ω02π | 2 π ∑ k = − ∞ + ∞ a k δ ( ω − k ω 0 ) 2\pi \sum_{k = -\infty}^{+ \infty}a_k\delta(\omega - k\omega_0) 2π∑k=−∞+∞akδ(ω−kω0) | a k a_k ak |
| e j ω 0 n , N = 2 π ω 0 e^{j\omega_0 n},N = \frac{2\pi}{\omega_0} ejω0n,N=ω02π | 2 π ∑ l = − ∞ + ∞ δ ( ω − ω 0 − 2 π l ) 2 \pi \sum_{l = -\infty}^{+\infty}\delta(\omega - \omega_0 - 2 \pi l) 2π∑l=−∞+∞δ(ω−ω0−2πl) | a k = 1 , k = 1 , 1 ± N , … a_k = 1,k = 1,1 \pm N,\ldots ak=1,k=1,1±N,… |
| cos ω 0 n , N = 2 π ω 0 \cos{\omega_0 n},N = \frac{2\pi}{\omega_0} cosω0n,N=ω02π | π ∑ l = − ∞ + ∞ ( δ ( ω − ω 0 − 2 π l ) + δ ( ω + ω − 2 π l ) ) \pi \sum_{l = -\infty}^{+\infty}(\delta(\omega - \omega_0 - 2 \pi l) + \delta(\omega + \omega - 2\pi l)) π∑l=−∞+∞(δ(ω−ω0−2πl)+δ(ω+ω−2πl)) | a k = 1 2 , k = 1 , 1 ± N , … a_k = \frac{1}{2},k = 1,1 \pm N,\ldots ak=21,k=1,1±N,… |
| sin ω 0 n , N = 2 π ω 0 \sin{\omega_0 n},N = \frac{2\pi}{\omega_0} sinω0n,N=ω02π | π j ∑ l = − ∞ + ∞ ( δ ( ω − ω 0 − 2 π l ) − δ ( ω + ω − 2 π l ) ) \frac{\pi}{j} \sum_{l = -\infty}^{+\infty}(\delta(\omega - \omega_0 - 2 \pi l) - \delta(\omega + \omega - 2\pi l)) jπ∑l=−∞+∞(δ(ω−ω0−2πl)−δ(ω+ω−2πl)) | a k = 1 2 j , k = 1 , 1 ± N , … ; a k = − 1 2 j , k = − 1 , − 1 ± N , … a_k = \frac{1}{2j},k = 1,1 \pm N,\ldots;a_k=-\frac{1}{2j},k=-1,-1\pm N,\ldots ak=2j1,k=1,1±N,…;ak=−2j1,k=−1,−1±N,… |
| x [ n ] = 1 x[n] = 1 x[n]=1 | 2 π ∑ l = − ∞ + ∞ δ ( ω − 2 π l ) 2 \pi \sum_{l = -\infty}^{+ \infty}\delta(\omega - 2\pi l) 2π∑l=−∞+∞δ(ω−2πl) | a k = 1 , k = 0 , ± N , … a_k = 1,k = 0,\pm N,\ldots ak=1,k=0,±N,… |
| 周期方波 x [ n ] = 1 , ∣ n ∣ ≤ N 1 , x [ n + N ] = x [ n ] x[n] = 1,|n| \le N_1,x[n + N] = x[n] x[n]=1,∣n∣≤N1,x[n+N]=x[n] | 2 π ∑ k = − ∞ + ∞ a k δ ( ω − 2 π N ) 2\pi \sum_{k = -\infty}^{+\infty}a_k \delta(\omega - \frac{2\pi}{N}) 2π∑k=−∞+∞akδ(ω−N2π) | a k = sin ( 2 π k / N ) ( N 1 + 1 2 ) N sin 2 π k / 2 N , k ≠ 0 , ± N , … ; a k = 2 N 1 + 1 N , k = 0 , ± N , … a_k = \frac{\sin{(2\pi k / N)(N_1 + \frac{1}{2})}}{N \sin{2\pi k/ 2N}},k \neq 0,\pm N,\ldots;a_k = \frac{2N_1 + 1}{N},k=0,\pm N,\ldots ak=Nsin2πk/2Nsin(2πk/N)(N1+21),k=0,±N,…;ak=N2N1+1,k=0,±N,… |
| ∑ k = − ∞ + ∞ δ [ n − k N ] \sum_{k = -\infty}^{+\infty} \delta[n - kN] ∑k=−∞+∞δ[n−kN] | 2 π N ∑ k = − ∞ + ∞ δ ( ω − 2 π k N ) \frac{2 \pi}{N}\sum_{k = -\infty}^{+\infty}\delta(\omega - \frac{2 \pi k}{N}) N2π∑k=−∞+∞δ(ω−N2πk) | a k = 1 N a_k = \frac{1}{N} ak=N1 |
| a n u [ n ] a^nu[n] anu[n],|a| < 1$ | 1 1 − a e − j ω \frac{1}{1 - ae^{-j\omega}} 1−ae−jω1 | - |
| x [ n ] = 1 , ∣ n ∣ ≤ N 1 x[n] = 1, |n| \le N_1 x[n]=1,∣n∣≤N1 | sin ω ( N 1 + 1 2 ) sin ω / 2 \frac{\sin{\omega(N_1 + \frac{1}{2})}}{\sin{\omega/2}} sinω/2sinω(N1+21) | - |
| sin W n π n , 0 < W < π \frac{\sin{Wn}}{\pi n},0 < W < \pi πnsinWn,0<W<π | X ( ω ) = 1 , 0 ≤ ∣ ω ∣ ≤ W X(\omega) = 1,0 \le |\omega| \le W X(ω)=1,0≤∣ω∣≤W 并且 X ( ω ) X(\omega) X(ω) 是周期的为 2 π 2\pi 2π | - |
| δ [ n ] \delta[n] δ[n] | 1 1 1 | - |
| u [ n ] u[n] u[n] | 1 1 − e − j ω + ∑ k = − ∞ + ∞ π δ ( ω − w π k ) \frac{1}{1 - e^{-j\omega}} + \sum_{k = -\infty}^{+ \infty}\pi \delta(\omega - w\pi k) 1−e−jω1+∑k=−∞+∞πδ(ω−wπk) | - |
| δ [ n − n 0 ] \delta[n - n_0] δ[n−n0] | e − j ω n 0 e^{-j\omega n_0} e−jωn0 | - |
| ( n + 1 ) a n u [ n ] , ∣ a ∣ < 1 (n+1)a^n u[n], |a| < 1 (n+1)anu[n],∣a∣<1 | 1 ( 1 − a e − j ω ) 2 \frac{1}{(1 - ae^{-j\omega})^2} (1−ae−jω)21 | - |
| ( n + r − 1 ) ! n ! ( r − 1 ) ! a n u [ n ] , ∣ a ∣ < 1 \frac{(n + r - 1)!}{n! (r - 1)!} a^n u[n], |a| < 1 n!(r−1)!(n+r−1)!anu[n],∣a∣<1 | 1 ( 1 − a e − j ω ) r \frac{1}{(1 - ae^{-j\omega})^r} (1−ae−jω)r1 | - |
由线性常系数差分方程表征的系统
由下面表示的线性常系数差分方程表征的系统:
∑ k = 0 N a k y [ n − k ] = ∑ k = 0 M b k x [ n − k ] \sum_{k = 0}^{N} a_k y[n - k] = \sum_{k = 0}^M b_k x[n - k] k=0∑Naky[n−k]=k=0∑Mbkx[n−k]
通过傅里叶变换时移和线性的性质可以表示为频域上:
∑ k = 0 N a k e − j k ω Y ( e j ω ) = ∑ k = 0 M b k e − j k ω X ( e j ω ) \sum_{k = 0}^N a_k e^{-jk\omega}Y(e^{j\omega}) = \sum_{k = 0}^M b_k e^{-jk\omega}X(e^{j\omega}) k=0∑Nake−jkωY(ejω)=k=0∑Mbke−jkωX(ejω)
或等效为:
H ( e j ω ) = Y ( e j ω ) X ( e j ω ) = ∑ k = 0 M b k e − j k ω ∑ k = 0 N a k e − j k ω H(e^{j\omega}) = \frac{Y(e^{j\omega})}{X(e^{j\omega})} = \frac{\sum_{k = 0}^M b_k e^{-jk\omega}}{\sum_{k = 0}^N a_k e^{-jk\omega}} H(ejω)=X(ejω)Y(ejω)=∑k=0Nake−jkω∑k=0Mbke−jkω
相关文章:

信号与系统复习笔记——傅里叶变换
信号与系统复习笔记——傅里叶变换 周期信号的傅里叶级数表示 特征函数 假设LTI系统的输入为 x ( t ) e s t x(t) e^{st} x(t)est 输出为: y ( t ) e s t ∗ h ( t ) ∫ − ∞ ∞ e s ( t − τ ) h ( τ ) d τ e s t ∫ − ∞ ∞ e − s τ h ( τ ) d…...
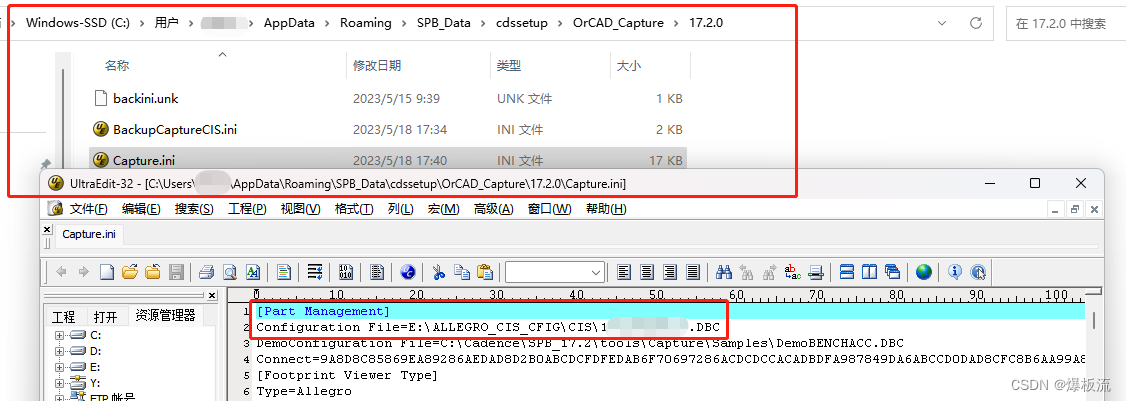
Allegor17.2版本WIN11系统CIS配置提示错误解决方案
错误提示: ERROR(ORCIS-6250): Unable to continue. Database access failed. Contact the database administrator to correct the following error(s), and then retry. ODBC Error Code: -1 Description: 在指定的 DSN 中,驱动程序和应用程序之间的体…...

Java设计模式七大原则-合成聚合复用原则
🧑💻作者:猫十二懿 ❤️🔥账号:CSDN 、掘金 、个人博客 、Github 🎉公众号:猫十二懿 合成-聚合复用原则 1、合成-聚合复用原则介绍 合成/聚合复用原则(Composition/Aggregatio…...

SOFA Weekly|可信基础设施技术分论坛、Layotto 社区会议回顾与预告、社区本周贡献...
SOFA WEEKLY | 每周精选 筛选每周精华问答,同步开源进展 欢迎留言互动~ SOFAStack(Scalable Open Financial Architecture Stack)是蚂蚁集团自主研发的金融级云原生架构,包含了构建金融级云原生架构所需的各个组件&am…...

Melody 监控(四十九)
当新的世界出现,请立即向他奔去 上一章简单介绍了Spring Boot Actuator详解(四十八), 如果没有看过,请观看上一章 一. JavaMelody 一.一 什么是 Java Melody JavaMelody是一个方便的Java或JavaEE Web 应用程序监控工具。 它允许自动存储由 Web 应用程序的实际操…...

Shell脚本管道符常用搭配命令
1.sort sort命令——以行为单位对文件内容进行排序,也可以根据不同的数据类型来排序比较原则是从首字符向后,依次按ASCII码值进行比较,最后将他们按升序输出。 sort [选项] 文件名 cat file | sort [选项] 常用选项 选项作用-n按照数字进行…...
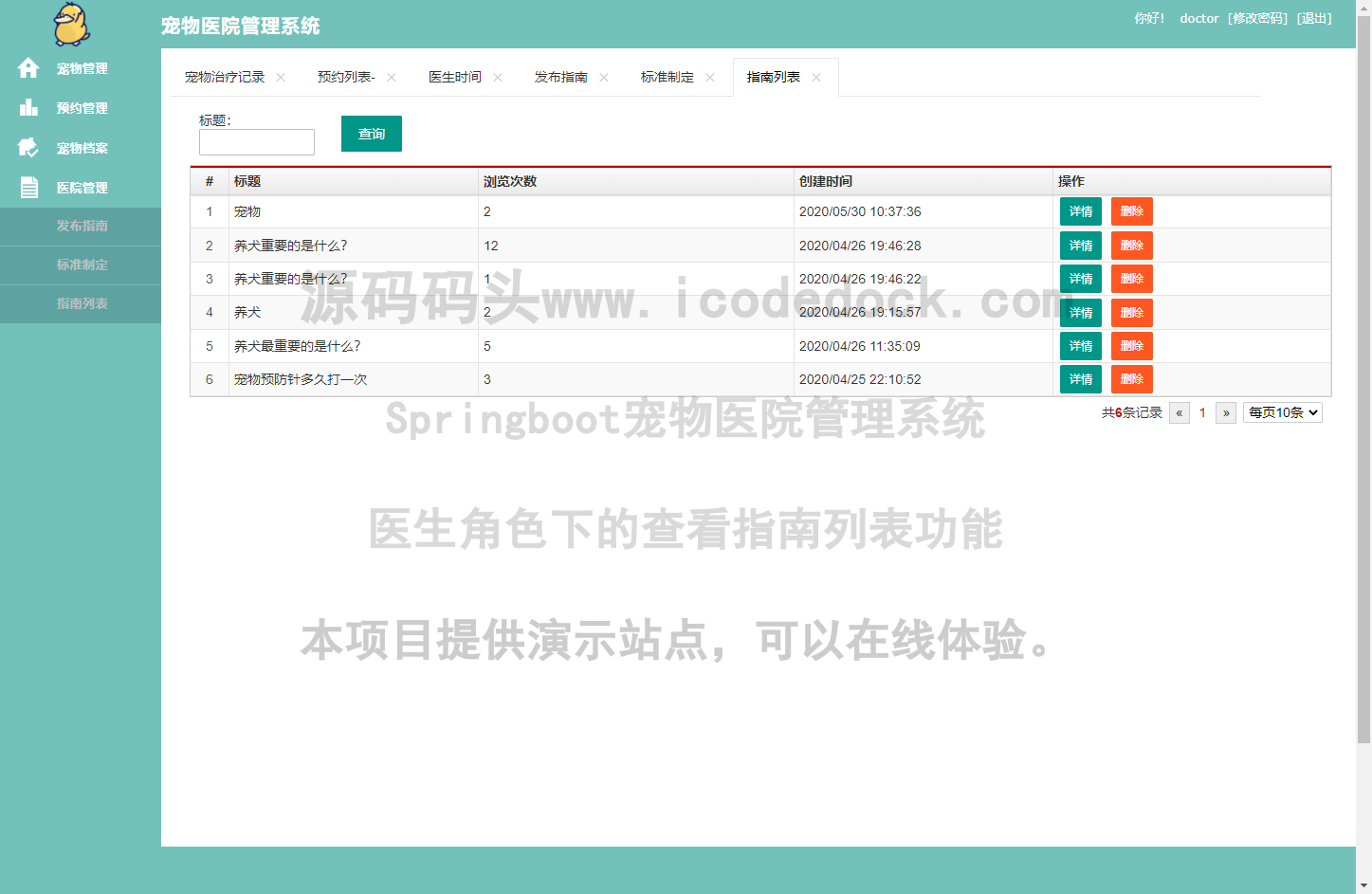
基于html+mysql+Spring+mybatis+Springboot的Springboot宠物医院管理系统
运行环境: 最好是java jdk 1.8,我在这个平台上运行的。其他版本理论上也可以。 IDE环境: Eclipse,Myeclipse,IDEA或者Spring Tool Suite都可以,如果编译器的版本太低,需要升级下编译器,不要弄太低的版本 tomcat服务器环…...
:搜索(5):其他)
算法模板(3):搜索(5):其他
搜索 模拟退火 模拟退火一个很关键的是,看看枚举到每一个方案是不是可能的。 3167. 星星还是树 在二维平面上有 n 个点,第 i 个点的坐标为 ( x i , y i ) (x_i,y_i) (xi,yi)。请你找出一个点,使得该点到这 n 个点的距离之和最小。这…...
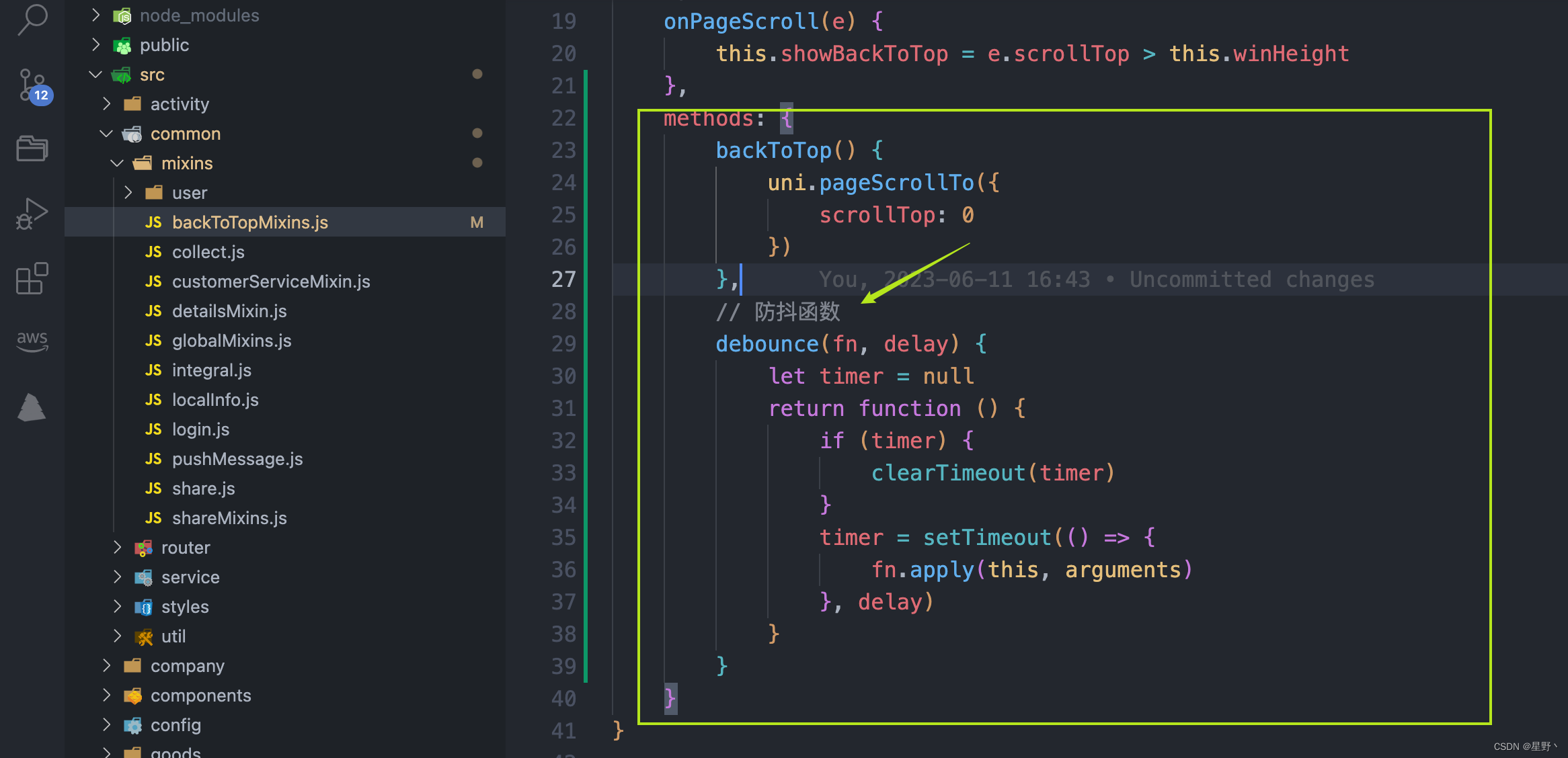
AWS CodeWhisperer 心得体会:安装与使用
大家好,今天我要和大家分享一下我在使用 AWS CodeWhisperer 这个工具时的心得体会。首先,让我们了解一下什么是 AWS CodeWhisperer。 什么是 AWS CodeWhisperer? AWS CodeWhisperer 是一个用于帮助开发者在 AWS 云平台上更轻松地编写、测试…...

高级查询 — 子查询
关于嵌套查询(子查询) 1.概述 子查询是在一个查询中嵌套另一个查询的查询语句。内部查询从外部查询或数据库中提取数据,然后使用这些数据来执行内部查询。出现在其他语句中的 select 语句,称为嵌套查询或子查询。外部的查询语句…...

霍夫变换(Hough Transform)
文章目录 1. 什么是霍夫变换2. 霍夫直线检测2.1 霍夫直线检测的具体步骤2.2 霍夫直线检测的优缺点2.3 OpenCV中霍夫直线检测的应用2.3.1 标准霍夫检测2.3.2 概率霍夫检测 3. 霍夫圆检测4. 源码仓库地址 1. 什么是霍夫变换 霍夫变换(Hough Transform)是图像处理中的一种特征提取…...

【每日挠头算法题(2)】压缩字符串|仅执行一次字符串交换能否使两个字符串相等
文章目录 一、压缩字符串思路 二、仅执行一次字符串交换能否使两个字符串相等思路1:计数法思路2:模拟法 总结 一、压缩字符串 点我直达~ 思路 使用双指针法 大致过程如下: 使用双指针,分别读(read)&…...

V4L2框架解析
和你一起终身学习,这里是程序员Android 经典好文推荐,通过阅读本文,您将收获以下知识点: 一、概览二、流程简介三、关键结构体四、模块初始化五、处理用户空间请求 一、概览 相机驱动层位于HAL Moudle与硬件层之间,借助linux内核驱…...
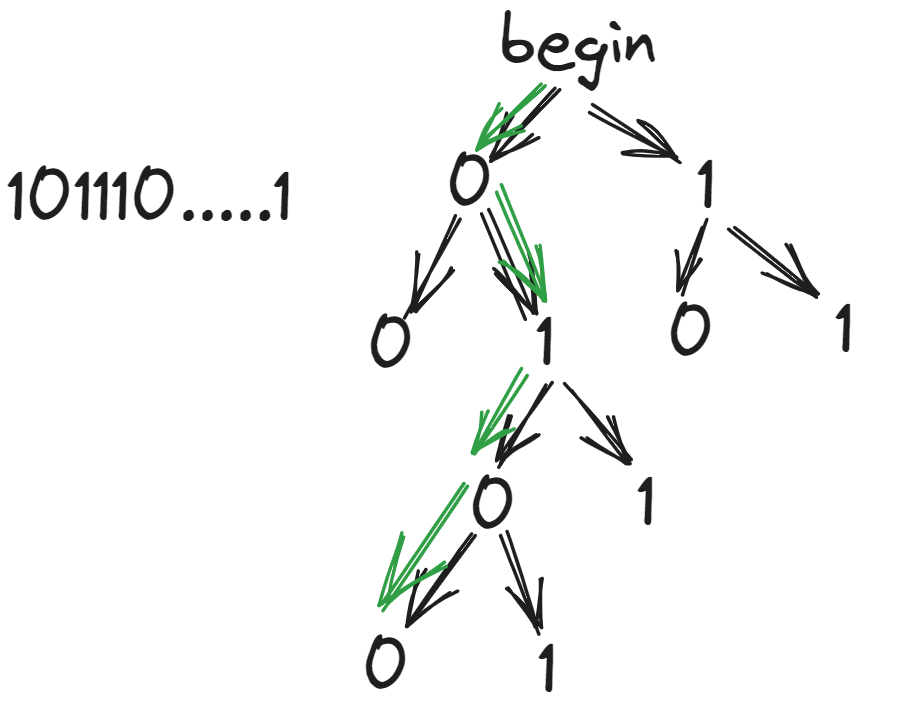
Trie树模板与应用
文章和代码已经归档至【Github仓库:https://github.com/timerring/algorithms-notes 】或者公众号【AIShareLab】回复 算法笔记 也可获取。 文章目录 Trie树(字典树)基本思想例题 Trie字符串统计code关于idx的理解 模板总结应用 最大异或对分…...
)
【华为OD统一考试B卷 | 200分】跳格子游戏(C++ Java JavaScript Python)
文章目录 题目描述输入描述输出描述用例C++javajavaScriptpython题目描述 地上共有N个格子,你需要跳完地上所有的格子,但是格子间是有强依赖关系的,跳完前一个格子后,后续的格子才会被开启,格子间的依赖关系由多组steps数组给出,steps[0]表示前一个格子,steps[1]表示st…...

该选哪个语言进修呢?
前言: 如今,计算机编程已经成为了许多工作领域中的必备技能。但是,现在的计算机语言有很多,这可能会让我们感到困惑:我应该从哪个语言开始呢?在这篇博客中,我们将详细分析当前流行的一些计算机…...

数据库实验三 数据查询一
任务描述 本关任务:按条件查询数据表的所有字段 为了完成本关任务,你需要掌握: 如何查询数据表的所有字段 相关知识 查询数据表 命令格式: select * from 数据表 where 查询条件 任务要求 打开province数据库 第一题 查询街…...

【Python百日进阶-Web开发-Peewee】Day244 - 数据库 Postgresql、CockroachDB
文章目录 六、数据库6.1 初始化数据库6.2 使用 Postgresql6.2.1 隔离级别 6.3 使用 CockroachDB 六、数据库 http://docs.peewee-orm.com/en/latest/peewee/database.html PeeweeDatabase对象表示与数据库的连接。该类Database使用打开数据库连接所需的所有信息进行实例化&…...

Vue 中的列表渲染
Vue 中的列表渲染 在 Vue 中,列表渲染是非常常见的操作。它允许我们将一个数组中的数据渲染为一个列表,从而实现数据的展示和交互。在本文中,我们将探讨 Vue 中的列表渲染的基本原理和用法,并给出一些实例代码来帮助读者更好地理…...

java 中的关键字
1. 面向对象编程(OOP) - 把程序中的实体看做对象,而不是过程或函数。OOP有3个基本特征:封装,继承和多态。 2. 类(Class) - 一个用于描述对象属性和方法的蓝图。 3. 对象(Object) - 类的实例化,也就是一个具体的实体。 4. 方法(Met…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...
