MATLAB 之 线性方程组求解
这里写目录标题
- 一、线性方程组求解
- 1. 线性方程组的直接解法
- 1.1 利用左除运算符的直接解法
- 1.2 利用矩阵的分解求解线性方程组
- 2. 线性方程组的迭代解法
- 2.1 Jacobi 迭代法
- 2.2 Gauss-Serdel 迭代法
- 3. 求线性方程的通解
一、线性方程组求解
- 在 MATLAB 中,关于线性方程组的解法一般分为两类:一类是直接法,就是在没有舍入误差的情况下,通过有限步的矩阵初等运算来求得方程组的解;另一类是迭代法,就是先给定一个解的初始值,然后按照一定的迭代算法进行逐步逼近,求出更精确的近似解。
1. 线性方程组的直接解法
- 线性方程组的直接解法大多基于高斯消元法、主元素消元法、平方根法和追赶法等。在 MATLAB 中,这些算法已经被编成了现成的库函数或运算符,因此,只需调用相应的函数或运算符即可完成线性方程组的求解。
1.1 利用左除运算符的直接解法
- 线性方程组求解最简单的方法就是使用左除运算符
\,系统会自动根据输入的系数矩阵判断选用哪种方法进行求解。 - 对于线性方程组 A x = b Ax=b Ax=b,可以利用左除运算符
\求解: x = A ∖ b x=A\setminus b x=A∖b - 当系数矩阵 A A A 为 N × N N×N N×N 的方阵时,MATLAB 会自行用高斯消元法求解线性方程组。若右端项 b b b 为 N × 1 N×1 N×1 的列向量,则 x = A ∖ b x=A\setminus b x=A∖b 可获得方程组的数值解 x x x( N × 1 N×1 N×1 的列向量)。
- 若右端项 b b b 为 N × M N×M N×M 的矩阵,则 x = A ∖ b x=A\setminus b x=A∖b 可同时获得系数矩阵 A A A 相同的 M M M 个线性方程组的数值解 x x x(为 N × M N×M N×M 的矩阵),即 x ( : , j ) = A ∖ b ( : , j ) , j = 1 , 2 , … , M x(:,j)=A\setminus b(:,j), j=1, 2, …, M x(:,j)=A∖b(:,j),j=1,2,…,M。
- 这里需要注意的是,如果矩阵 A A A 是奇异的或接近奇异的,则 MATLAB 会给出警告信息。
- 例如,我们用直接解法求解下列线性方程组。 { 2 x 1 + x 2 − 5 x 3 + x 4 = 13 x 1 − 5 x 2 + 7 x 4 = − 9 2 x 2 + x 3 − x 4 = 6 x 1 + 6 x 2 − x 3 − 4 x 4 = 0 \left\{\begin{matrix}2x_{1}+x_{2}-5x_{3}+x_{4}=13 \\x_{1}-5x_{2}+7x_{4}=-9 \\2x_{2}+x_{3}-x_{4}=6 \\x_{1}+6x_{2}-x_{3}-4x_{4}=0 \end{matrix}\right. ⎩ ⎨ ⎧2x1+x2−5x3+x4=13x1−5x2+7x4=−92x2+x3−x4=6x1+6x2−x3−4x4=0
- 程序如下:
>> A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4];
>> b=[13,-9,6,0]';
>> x=A\b
- 程序运行结果如下:
x =-66.555625.6667-18.777826.55561.2 利用矩阵的分解求解线性方程组
- 矩阵分解是指根据一定的原理用某种算法将一个矩阵分解成若干个矩阵的乘积。常见的矩阵分解有 LU 分解、QR 分解、Cholesky 分解,以及 Schur 分解、Hessenberg 分解、奇异分解等。
- 通过这些分解方法求解线性方程组的有点是运算速度快,可以节省存储空间。
- (1) LU 分解。矩阵的 LU 分解就是将一个矩阵表示为一个变换下三角阵和一个上三角阵的乘积形式。线性代数中已经证明,只要方阵 X X X 是非奇异的,LU 分解总是可以进行的。
- MATLAB 提供的
lu函数用于对矩阵进行 LU 分解,其调用格式如下。 - ①
[L,U]=lu(X):产生一个上三角阵 U 和一个变换形式的下三角阵 L(行交换),使之满足 X = L U X=LU X=LU。注意,这里的矩阵 X X X 必须是方阵。 - ②
[L,U,P]=lu(X):产生一个上三角阵 U 和一个下三角阵 L 以及一个置换矩阵 P,使之满足 P X = L U PX=LU PX=LU。当然矩阵 X X X 同样必须是方阵。 - 当使用第一种格式时,矩阵 L L L 往往不是一个下三角阵,但可以通过行交换成为一个下三角阵。
- 例如,我们设 A = [ 1 − 1 1 5 − 4 3 2 1 1 ] A=\begin{bmatrix} 1 & -1 & 1\\ 5 & -4 & 3\\ 2 & 1 &1 \end{bmatrix} A= 152−1−41131
- 则对矩阵 A A A 进行 LU 分解的程序如下:
>> A=[1,-1,1;5,-4,3;2,1,1];
>> [L,U]=lu(A)L =0.2000 -0.0769 1.00001.0000 0 00.4000 1.0000 0U =5.0000 -4.0000 3.00000 2.6000 -0.20000 0 0.3846- 为检验结果是否正确,输入如下程序:
>> LU=L*ULU =1 -1 15 -4 32 1 1- 说明结果是正确的。例中所获得的矩阵 L L L 并不是一个下三角阵,但经过各行互换之后,即可获得一个下三角阵。
- 利用第二种格式对矩阵 A A A 进行 LU 分解,程序如下:
>> [L,U,P]=lu(A)L =1.0000 0 00.4000 1.0000 00.2000 -0.0769 1.0000U =5.0000 -4.0000 3.00000 2.6000 -0.20000 0 0.3846P =0 1 00 0 11 0 0>> LU=L*U %这种分解其乘积不为ALU =5 -4 32 1 11 -1 1>> inv(P)*L*U %考虑矩阵P后的结果ans =1 -1 15 -4 32 1 1- 实现 LU 分解后,线性方程组 A x = b Ax=b Ax=b 的解 x = U ∖ ( L ∖ b ) x=U\setminus (L\setminus b) x=U∖(L∖b) 或 x = U ∖ ( L ∖ P b ) x=U\setminus (L\setminus Pb) x=U∖(L∖Pb),这样可以大大提高运算速度。
- 例如,我们用 LU 分解求解下列线性方程组。 { 2 x 1 + x 2 − 5 x 3 + x 4 = 13 x 1 − 5 x 2 + 7 x 4 = − 9 2 x 2 + x 3 − x 4 = 6 x 1 + 6 x 2 − x 3 − 4 x 4 = 0 \left\{\begin{matrix}2x_{1}+x_{2}-5x_{3}+x_{4}=13 \\x_{1}-5x_{2}+7x_{4}=-9 \\2x_{2}+x_{3}-x_{4}=6 \\x_{1}+6x_{2}-x_{3}-4x_{4}=0 \end{matrix}\right. ⎩ ⎨ ⎧2x1+x2−5x3+x4=13x1−5x2+7x4=−92x2+x3−x4=6x1+6x2−x3−4x4=0
- 程序如下:
>> A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4];
>> b=[13,-9,6,0]';
>> [L,U]=lu(A)L =1.0000 0 0 00.5000 1.0000 0 00 -0.3636 0.4773 1.00000.5000 -1.0000 1.0000 0U =2.0000 1.0000 -5.0000 1.00000 -5.5000 2.5000 6.50000 0 4.0000 2.00000 0 0 0.4091>> x=U\(L\b)x =-66.555625.6667-18.777826.5556- 或采用 LU 分解的第二种格式,程序如下:
>> [L,U,P]=lu(A);
>> x=U\(L\P*b);
- 将得到与上面相同的结果。
- (2) QR 分解。对矩阵 X X X 进行 QR 分解,就是把 X X X 分解为一个正交矩阵 Q Q Q 和一个上三角矩阵 R R R 的乘积形式。QR 分解只能对方阵进行。MATLAB 的函数
qr可用于对矩阵进行 QR 分解,其调用格式如下。 - ①
[Q,R]=qr(X):产生一个正交矩阵 Q Q Q 和一个上三角阵 R R R,使之满足 X = Q R X=QR X=QR。 - ②
[Q,R,E]=qr(X):产生一个正交矩阵 Q Q Q、一个上三角阵 R R R 以及一个置换矩阵 E E E,使之满足 X E = Q R XE=QR XE=QR。 - 例如,我们设 A = [ 1 − 1 1 5 − 4 3 2 7 10 ] A=\begin{bmatrix} 1 & -1 & 1\\ 5 & -4 & 3\\ 2 & 7 &10 \end{bmatrix} A= 152−1−471310
- 则对矩阵 A A A 进行 Q R QR QR 分解的命令如下:
>> A=[1,-1,1;5,-4,3;2,7,10];
>> [Q,R]=qr(A)Q =-0.1826 -0.0956 -0.9785-0.9129 -0.3532 0.2048-0.3651 0.9307 -0.0228R =-5.4772 1.2780 -6.57270 8.0229 8.15170 0 -0.5917- 为检验结果是否正确,输入如下程序:
>> QR=Q*RQR =1.0000 -1.0000 1.00005.0000 -4.0000 3.00002.0000 7.0000 10.0000- 说明结果是正确的。此时,我们利用第二种格式对矩阵 A A A 进行 QR 分解:
>> [Q,R,E]=qr(A)Q =-0.0953 -0.2514 -0.9632-0.2860 -0.9199 0.2684-0.9535 0.3011 0.0158R =-10.4881 -5.4347 -3.43250 6.0385 -4.24850 0 0.4105E =0 0 10 1 01 0 0>> Q*R/E %验证A=Q*R*inv(E)ans =1.0000 -1.0000 1.00005.0000 -4.0000 3.00002.0000 7.0000 10.0000- 在实现 QR 分解后,线性方程组 A x = b Ax=b Ax=b 的解为 x = R ∖ ( Q ∖ b ) x=R\setminus (Q\setminus b) x=R∖(Q∖b) 或 x = E ∖ ( R ∖ ( Q ∖ b ) ) 。 x=E\setminus (R\setminus (Q\setminus b))。 x=E∖(R∖(Q∖b))。
- 例如,我们用 QR 分解求解下列线性方程组。 { 2 x 1 + x 2 − 5 x 3 + x 4 = 13 x 1 − 5 x 2 + 7 x 4 = − 9 2 x 2 + x 3 − x 4 = 6 x 1 + 6 x 2 − x 3 − 4 x 4 = 0 \left\{\begin{matrix}2x_{1}+x_{2}-5x_{3}+x_{4}=13 \\x_{1}-5x_{2}+7x_{4}=-9 \\2x_{2}+x_{3}-x_{4}=6 \\x_{1}+6x_{2}-x_{3}-4x_{4}=0 \end{matrix}\right. ⎩ ⎨ ⎧2x1+x2−5x3+x4=13x1−5x2+7x4=−92x2+x3−x4=6x1+6x2−x3−4x4=0
- 程序如下:
>> A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4];
>> b=[13,-9,6,0]';
>> [Q,R]=qr(A);
>> x=R\(Q\b)
- 程序运行结果如下:
x =-66.555625.6667-18.777826.5556- 或采用 QR 分解的第二种格式,程序如下:
>> [Q,R,E]=qr(A);
>> x=E*(R\(Q\b))x =-66.555625.6667-18.777826.5556- 将得到与上面相同的结果。
- (3) Cholesky 分解。如果矩阵 X X X 是对称正定的,则 Cholesky 分解将矩阵 X X X 分解成一个下三角阵和一个上三角阵的乘积。设上三角阵为 R R R,则下三角阵为其转置,即 X = R ′ R X=R'R X=R′R。MATLAB 函数
chol(X)用于对矩阵 X X X 进行 Cholesky 分解,其调用格式如下。 - ①
R=chol(X):产生一个上三角阵 R R R,使 R ′ R = X R'R=X R′R=X。若 X X X 为非对称正定,则输出一个出错信息。 - ②
[R,p]=chol(X):这个命令格式将不输出出错信息。若 X X X 为对称正定的,则 p = 0 p=0 p=0, R R R 与上述格式得到的结果相同,否则 p p p 为一个正整数。如果 X X X 为满秩矩阵,则 R R R 为一个阶数为 q = p − 1 q=p-1 q=p−1 的上三角阵,且满足 R ′ R = X ( 1 : q , 1 : q ) R'R =X(1:q,1:q) R′R=X(1:q,1:q)。 - 例如,我们设 A = [ 2 1 1 1 2 − 1 1 − 1 3 ] A=\begin{bmatrix} 2 & 1 & 1\\ 1 & 2 & -1\\ 1 & -1 &3 \end{bmatrix} A= 21112−11−13
- 则对矩阵 A A A 进行 Cholesky 分解的命令如下:
>> A=[2,1,1;1,2,-1;1,-1,3];
>> R=chol(A)R =1.4142 0.7071 0.70710 1.2247 -1.22470 0 1.0000- 可以验证 R ′ R = A R'R =A R′R=A,输入如下程序:
>> R'*Rans =2.0000 1.0000 1.00001.0000 2.0000 -1.00001.0000 -1.0000 3.0000- 说明结果是正确的。此时,我们利用第二种格式对矩阵 A A A 进行 Cholesky 分解:
>> [R,p]=chol(A)R =1.4142 0.7071 0.70710 1.2247 -1.22470 0 1.0000p =0- 结果中出现 p = 0 p=0 p=0,这表示矩阵 A A A 是一个正定矩阵。如果试图对一个非正定矩阵进行 Cholesky 分解,则将得出错误信息,所以,
chol函数还可以用来判定矩阵是否为正定矩阵。 - 实现 Cholesky 分解后,线性方程组 A x = b Ax=b Ax=b 的解为 R ′ R x = b R'Rx=b R′Rx=b,所以 x = R ∖ ( R ′ ∖ b ) 。 x=R\setminus (R'\setminus b)。 x=R∖(R′∖b)。
- 例如,我们用 Cholesky 分解求解下列线性方程组。 { 2 x 1 + x 2 − 5 x 3 + x 4 = 13 x 1 − 5 x 2 + 7 x 4 = − 9 2 x 2 + x 3 − x 4 = 6 x 1 + 6 x 2 − x 3 − 4 x 4 = 0 \left\{\begin{matrix}2x_{1}+x_{2}-5x_{3}+x_{4}=13 \\x_{1}-5x_{2}+7x_{4}=-9 \\2x_{2}+x_{3}-x_{4}=6 \\x_{1}+6x_{2}-x_{3}-4x_{4}=0 \end{matrix}\right. ⎩ ⎨ ⎧2x1+x2−5x3+x4=13x1−5x2+7x4=−92x2+x3−x4=6x1+6x2−x3−4x4=0
- 程序如下:
>> A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4];
>> b=[13,-9,6,0]';
>> R=chol(A)
错误使用 chol
矩阵必须为正定矩阵。
- 命令执行时,出现错误信息,说明 A A A 为非正定矩阵。
2. 线性方程组的迭代解法
- 迭代法是一种不断用变量的旧值递推新值的过程,是用计算机解决问题的一种基本方法。它利用计算机运算速度快,适合做重复性操作的特点,让一组指令重复执行,在每次执行这组指令时,都从变量的原值推出它的新值。
- 迭代解法非常适合求解大型稀疏矩阵的方程组。在数值分析中,迭代解法主要包括 Jacobi 迭代法、Gauss-Serdel 迭代法、超松弛迭代法和两步迭代法。
- 首先,我们用一个例子说明迭代法的思想。
- 为了求解线性方程组 { 10 x 1 − x 2 = 9 − x 1 + 10 x 2 − 2 x 3 = 7 − 2 x 2 + 10 x 3 = 6 \left\{\begin{matrix}10x_{1}-x_{2}=9 \\-x_{1}+10x_{2}-2x_{3}=7 \\-2x_{2}+10x_{3}=6 \end{matrix}\right. ⎩ ⎨ ⎧10x1−x2=9−x1+10x2−2x3=7−2x2+10x3=6
- 将方程改写为 { x 1 = 10 x 2 − 2 x 3 − 7 x 2 = 10 x 1 − 9 x 3 = 1 10 ( 6 + 2 x 2 ) \left\{\begin{matrix}x_{1}=10x_{2}-2x_{3}-7 \\x_{2}=10x_{1}-9 \\x_{3}=\frac{1}{10}(6+2x_{2}) \end{matrix}\right. ⎩ ⎨ ⎧x1=10x2−2x3−7x2=10x1−9x3=101(6+2x2)
- 这种形式的好处是将一组 x x x 代入右端,可以立即得到另一组 x x x。如果两组 x x x 相等,那么它就是方程组的解,不等时可以继续迭代。
- 例如,选取初值 x 1 = x 2 = x 3 = 0 x_{1}=x_{2}=x_{3}=0 x1=x2=x3=0,则经过一次迭代后, 得到 x 1 = − 7 x_{1}=-7 x1=−7, x 2 = − 9 x_{2}=-9 x2=−9, x 3 = 0.6 x_{3}=0.6 x3=0.6,然后再继续迭代。可以构造方程的迭代公式为 { x 1 ( k + 1 ) = 10 x 2 ( k ) − 2 x 3 ( k ) − 7 x 2 ( k + 1 ) = 10 x 1 ( k ) − 9 x 3 ( k + 1 ) = 1 10 ( 6 + 2 x 2 ( k ) ) \left\{\begin{matrix}x_{1}^{(k+1)}=10x_{2}^{(k)}-2x_{3}^{(k)}-7 \\x_{2}^{(k+1)}=10x_{1}^{(k)}-9 \\x_{3}^{(k+1)}=\frac{1}{10}(6+2x_{2}^{(k)}) \end{matrix}\right. ⎩ ⎨ ⎧x1(k+1)=10x2(k)−2x3(k)−7x2(k+1)=10x1(k)−9x3(k+1)=101(6+2x2(k))
2.1 Jacobi 迭代法
- 对于线性方程组 A x = b Ax=b Ax=b,如果 A A A 是非奇异方阵,且 a i i ≠ 0 ( i = 1 , 2 , … , n ) a_{ii}\ne 0(i=1,2,…,n) aii=0(i=1,2,…,n),则可将 A A A 分解为 A = D − L − U A=D-L-U A=D−L−U,其中 D D D 为对角阵,其元素为 A A A 的对角元素, L L L 与 U U U 为 A A A 的下三角阵取反和上三角阵取反: L = − [ 0 a 2 , 1 0 ⋮ ⋱ ⋱ a n , 1 ⋯ a n , n − 1 0 ] L=-\begin{bmatrix} 0 & & & \\ a_{2,1} & 0 & & \\ \vdots & \ddots & \ddots & \\ a_{n,1} & \cdots & a_{n,n-1} &0 \end{bmatrix} L=− 0a2,1⋮an,10⋱⋯⋱an,n−10 U = − [ 0 a 1 , 2 ⋯ a 1 , n 0 ⋱ ⋮ ⋱ a n − 1 , n 0 ] U=-\begin{bmatrix} 0 & a_{1,2} & \cdots &a_{1,n} \\ & 0 & \ddots& \vdots\\ & & \ddots &a_{n-1,n} \\ & & &0 \end{bmatrix} U=− 0a1,20⋯⋱⋱a1,n⋮an−1,n0
- 于是 A x = b Ax=b Ax=b 转化为 x = D − 1 ( L + U ) x + D − 1 b x=D^{-1}(L+U)x+D^{-1}b x=D−1(L+U)x+D−1b
- 与之对应的迭代公式为 x k + 1 = D − 1 ( L + U ) x k + D − 1 b x^{k+1}=D^{-1}(L+U)x^{k}+D^{-1}b xk+1=D−1(L+U)xk+D−1b
- 这就是 Jacobi 迭代公式。如果序列 { x k + 1 } \left \{x^{k+1}\right \} {xk+1} 收敛于 x x x,则 x x x 必是方程 A x = b Ax=b Ax=b 的解。
- Jacobi 迭代法的 MATLAB 函数文件 jacobi.m 如下:
function [y,n]=jacobi(A,b,x0,ep)
if nargin==3ep=1.0e-6;
elseif nargin<3errorreturn
end
D=diag(diag(A)); %求A的对角矩阵
L=-tril(A,-1); %求A的下三角阵
U=-triu(A,1); %求A的上三角阵
B=D\(L+U);
f=D\b;
y=B*x0+f;
n=1; %迭代次数
while norm(y-x0)>=epx0=y;y=B*x0+f;n=n+1;
end
- 例如,我们用 Jacobi 迭代法求解下列线性方程组。设迭代初值为 0,迭代精度为 1 0 − 6 10^{-6} 10−6。 { 10 x 1 − x 2 = 9 − x 1 + 10 x 2 − 2 x 3 = 7 − 2 x 2 + 10 x 3 = 6 \left\{\begin{matrix}10x_{1}-x_{2}=9 \\-x_{1}+10x_{2}-2x_{3}=7 \\-2x_{2}+10x_{3}=6 \end{matrix}\right. ⎩ ⎨ ⎧10x1−x2=9−x1+10x2−2x3=7−2x2+10x3=6
- 在程序中,我们调用函数文件 jacobi.m,程序如下:
>> A=[10,-1,0;-1,10,-2;0,-2,10];
>> b=[9,7,6]';
>> [x,n]=jacobi(A,b,[0,0,0]',1.0e-6)
- 程序运行结果如下:
x =0.99580.95790.7916n =112.2 Gauss-Serdel 迭代法
- 在 Jacobi 迭代过程中,计算 x i ( k + 1 ) x^{(k+1)}_{i} xi(k+1) 时, x 1 ( k + 1 ) , … , x i − 1 ( k + 1 ) x^{(k+1)}_{1},…,x^{(k+1)}_{i-1} x1(k+1),…,xi−1(k+1) 已经得到,不必再用 x 1 ( k ) , … , x i − 1 ( k ) x^{(k)}_{1},…,x^{(k)}_{i-1} x1(k),…,xi−1(k),即原来的迭代公式 D x ( k + 1 ) = ( L + U ) X ( k ) + b Dx^{(k+1)}=(L+U)X^{(k)}+b Dx(k+1)=(L+U)X(k)+b 可以改进为 D x ( k + 1 ) = L ( k + 1 ) + X ( k ) + b Dx^{(k+1)}=L^{(k+1)}+X^{(k)}+b Dx(k+1)=L(k+1)+X(k)+b,于是得到 x ( k + 1 ) = ( D − L ) − 1 U x ( k ) + ( D − L ) − 1 b x^{(k+1)}=(D-L)^{-1}Ux^{(k)}+(D-L)^{-1}b x(k+1)=(D−L)−1Ux(k)+(D−L)−1b
- 该式即为 Gauss-Serdel 迭代公式。和 Jacobi 迭代公式相比,Gauss-Serdel 迭代用新分量代替旧分量,精度会高些。
- Gauss-Serdel 迭代法的 MATLAB 函数文件 gauseidel.m 如下:
function [y,n]=gauseidel(A,b,x0,ep)
if nargin==3ep=1.0e-6;
elseif nargin<3errorreturn
end
D=diag(diag(A)); %求A的对角矩阵
L=-tril(A,-1); %求A的下三角阵
U=-triu(A,1); %求A的上三角阵
G=(D-L)\U;
f=(D-L)\b;
y=G*x0+f;
n=1; %迭代次数
while norm(y-x0)>=epx0=y;y=G*x0+f;n=n+1;
end
- 例如,我们用 Gauss-Serdel 迭代法求解下列线性方程组。设迭代初值为 0,迭代精度为 1 0 − 6 10^{-6} 10−6。 { 10 x 1 − x 2 = 9 − x 1 + 10 x 2 − 2 x 3 = 7 − 2 x 2 + 10 x 3 = 6 \left\{\begin{matrix}10x_{1}-x_{2}=9 \\-x_{1}+10x_{2}-2x_{3}=7 \\-2x_{2}+10x_{3}=6 \end{matrix}\right. ⎩ ⎨ ⎧10x1−x2=9−x1+10x2−2x3=7−2x2+10x3=6
- 在程序中,我们调用函数文件 gauseidel.m,程序如下:
>> A=[10,-1,0;-1,10,-2;0,-2,10];
>> b=[9,7,6]';
>> [x,n]=gauseidel(A,b,[0,0,0]',1.0e-6)
- 程序运行结果如下:
x =0.99580.95790.7916n =7- 由此可见,一般情况下 Gauss-Serdel 迭代比 Jacobi 迭代要收敛快一些。但这也是不绝对的,在某些情况下,Jacobi 迭代收敛而 Gauss-Serdel 迭代却可能不收敛。
- 例如,我们分别用 Jacobi 迭代和 Gauss-Serdel 迭代法求解下列线性方程组,看是否收敛。 [ 1 2 − 2 1 1 1 1 2 1 ] [ x 1 x 2 x 3 ] = [ 9 7 6 ] \begin{bmatrix} 1 & 2&-2 \\ 1 & 1 & 1\\ 1&2 &1 \end{bmatrix}\begin{bmatrix}x_{1} \\x_{2} \\x_{3} \end{bmatrix}=\begin{bmatrix}9 \\7 \\6 \end{bmatrix} 111212−211 x1x2x3 = 976
- 程序如下:
>> a=[1,2,-2;1,1,1;2,2,1];
>> b=[9;7;6];
>> [x,n]=jacobi(a,b,[0;0;0])x =-27268n =4>> [x,n]=gauseidel(a,b,[0;0;0])x =NaNNaNNaNn =1012- 可见对此方程,用 Jacobi 迭代收敛,而 Gauss-Serdel 迭代不收敛。因此,在使用迭代法时,要考虑算法的收敛性。
3. 求线性方程的通解
- 线性方程组的求解分为两类:一类是求方程组的唯一解(即特解),另一类是求方程组的无穷解(即通解)。这里对线性方程组 A x = b Ax=b Ax=b 的求解理论进行归纳。
- (1) 当系数矩阵 A A A 是一个满秩方阵时,方程 A x = b Ax=b Ax=b 称为恰定方程,方程有唯一 解 x = A − 1 b x=A^{-1}b x=A−1b,这是最基本的一种情况。一般用 x = A ∖ b x=A\setminus b x=A∖b 求解速度更快。
- (2) 当方程组右端向量 b = 0 b=0 b=0 时,方程称为齐次方程组。齐次方程组总有零解,因此称解 x = 0 x=0 x=0 为平凡解。当系数矩阵 A A A 的秩小于 n n n( n n n 为方程组中未知变量的个数)时,齐次方程组有无穷多个非平凡解,其通解中包含 n n n-rank(4) 个线性无关的解向量,用 MATLAB 的函数
null(A,'r')可求得基础解系。 - (3) 当方程组右端向量 b ≠ 0 b≠0 b=0 时,系数矩阵的秩 rank(4) 与其增广矩阵的秩 rank([A,b]) 是判断其是否有解的基本条件。
- ① 当 rank<(A)=rank([4,b])=n 时,方程组有唯一解: x r = A ∖ b xr=A\setminus b xr=A∖b 或 x = p i n v ( A ) ∗ b x=pinv(A)*b x=pinv(A)∗b。
- ② 当 rank(4)=rank([A,b])<n 时,方程组有无穷多个解,其通解 = 方程组的一个特解 + 对应的齐次方程组 A x = 0 Ax=0 Ax=0 的通解。可以用 A ∖ b A\setminus b A∖b 求得方程组的一个特解,用
null(A,'r')求得该方程组所对应的齐次方程组的基础解系,基础解系中包含 n n n-rank(4) 个线性无关的解向量。 - ③ 当 rank(A)<rank([A,b]) 时,方程组无解。
- 下面,我们写一个求解线性方程组的函数文件 line_solution.m。
function [x,y]=line_solution(A,b)
[m,n]=size(A) ;
y=[];
if norm(b)>0 %非齐次方程组if rank(A)==rank([A,b])if rank(A)==n %有唯一解disp('原方程组有唯一解x');x=A\b; else %方程组有无穷多个解,基础解系disp('原方程组有无穷个解,特解为x,其齐次方程组的基础解系为y');x=A\b; y=null(A,'r');endelsedisp('方程组无解'); %方程组无解x=[];end
else %齐次方程组disp('原方程组有零解x') ;x=zeros(n,1); %0解if rank(A)<ndisp('方程组有无穷个解,基础解系为y'); %非0解y=null(A,'r');end
end
- 例如,我们求解方程组。 { x 1 − 2 x 2 + 3 x 3 − x 4 = 1 3 x 1 − x 2 + 5 x 3 − 3 x 4 = 2 2 x 1 + x 2 + 2 x 3 − 2 x 4 = 3 \left\{\begin{matrix}x_{1}-2x_{2}+3x_{3}-x_{4}=1 \\3x_{1}-x_{2}+5x_{3}-3x_{4}=2 \\2x_{1}+x_{2}+2x_{3}-2x_{4}=3 \end{matrix}\right. ⎩ ⎨ ⎧x1−2x2+3x3−x4=13x1−x2+5x3−3x4=22x1+x2+2x3−2x4=3
- 程序如下:
>> A=[1,-2,3,-1;3,-1,5,-3;2,1,2,-2];
>> b=[1;2;3];
>> [x,y]=line_solution(A,b)
- 程序运行结果如下:
方程组无解x =[]y =[]- 表明该方程无解。
- 例如,我们求方程组的通解。 { x 1 + x 2 − 3 x 3 − x 4 = 1 3 x 1 − x 2 − 3 x 3 + 4 x 4 = 4 x 1 + 5 x 2 − 9 x 3 − 8 x 4 = 0 \left\{\begin{matrix}x_{1}+x_{2}-3x_{3}-x_{4}=1 \\3x_{1}-x_{2}-3x_{3}+4x_{4}=4 \\x_{1}+5x_{2}-9x_{3}-8x_{4}=0 \end{matrix}\right. ⎩ ⎨ ⎧x1+x2−3x3−x4=13x1−x2−3x3+4x4=4x1+5x2−9x3−8x4=0
- 程序如下:
>> format rat %指定有理式格式输出
>> A=[1,1,-3,-1;3,-1,-3,4;1,5,-9,-8];
>> b=[1;4;0];
>> [x,y]=line_solution(A,b)
>> x,y
>> format short %恢复默认的短格式输出
- 程序运行结果如下:
警告: 秩亏,秩 = 2,tol = 8.837264e-15。
> 位置:line_solution (第 11 行)x =0 0 -8/15 3/5 y =3/2 -3/4 3/2 7/4 1 0 0 1 - 所以原方程的通解为 X = k 1 [ 3 / 2 3 / 2 1 0 ] + k 2 [ − 3 / 4 7 / 4 0 1 ] + [ 0 0 − 8 / 15 3 / 5 ] X=k_{1}\begin{bmatrix}3/2 \\3/2 \\1 \\0 \end{bmatrix}+k_{2}\begin{bmatrix}-3/4 \\7/4 \\0 \\1 \end{bmatrix}+\begin{bmatrix}0 \\0 \\-8/15 \\3/5 \end{bmatrix} X=k1 3/23/210 +k2 −3/47/401 + 00−8/153/5
- 其中, k 1 、 k 2 k_{1}、k_{2} k1、k2 为任意常数。
相关文章:

MATLAB 之 线性方程组求解
这里写目录标题 一、线性方程组求解1. 线性方程组的直接解法1.1 利用左除运算符的直接解法1.2 利用矩阵的分解求解线性方程组 2. 线性方程组的迭代解法2.1 Jacobi 迭代法2.2 Gauss-Serdel 迭代法 3. 求线性方程的通解 一、线性方程组求解 在 MATLAB 中,关于线性方程…...

华为OD机试真题 Java 实现【字符串序列判定】【2022Q4 100分】,附详细解题思路
一、题目描述 输入两个字符串a和b,都只包含英文小写字母。a长度<=100,b长度<=500,000。 判定a是否是b的有效子串。 判定规则: a中的每个字符在b中都能找到(可以不连续),且a在b中字符的前后顺序与a中顺序要保持一致。 (例如,a=”qwt”是b=”qwerty”的一个子…...
taro使用小记 —— 持续更新
目录 1、在 taro 中使用 axios2、在 taro 中添加全局组件自动引入和方法自动引入3、在 taro 中使用 pinia 1、在 taro 中使用 axios taro 3.6 版本已经支持了网络请求库。 需安装插件 tarojs/plugin-http 使用和注意事项说明: https://www.npmjs.com/package/taroj…...

【LeetCode】110. 平衡二叉树
110. 平衡二叉树(简单) 思路 对二叉树做先序遍历,从底至顶返回子树最大高度,若判定某子树不是平衡树则“剪枝”直接向上返回。 递归返回值: 当节点 root 左、右子树的高度差 > 1:返回 -1,代…...

SQL视图、存储过程、触发器
一、视图 (一)介绍 视图(view)是一种虚拟存在的表。视图中的数据并不在数据库中实际存在,行和列数据来自定义视图的查询中使用的表,并且是在使用视图时动态生成的。 通俗的讲,视图只保存了查询的SQL逻辑&…...
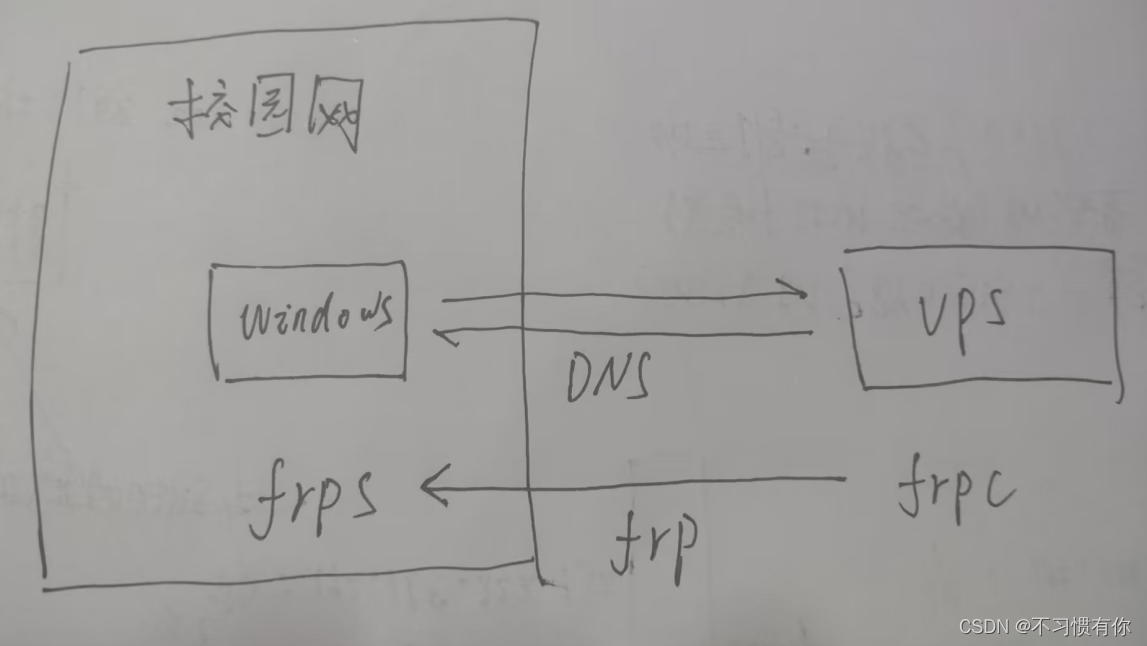
DNS隧道穿透
介绍: DNS隧道,是隧道技术中的一种。当我们的HTTP、HTTPS这样的上层协议、正反向端口转发都失败的时候,可以尝试使用DNS隧道。DNS隧道很难防范,因为平时的业务也好,使用也罢,难免会用到DNS协议进行解析&am…...

1.2 Scala变量与数据类型
一、变量声明 (一)简单说明 Scala中变量的声明使用关键字val和var。val类似Java中的final变量,也就是常量,一旦初始化将不可修改;var类似Java中的非final变量,可以被多次赋值,多次修改。 val - …...

深入探讨软件测试的质量度量指标
本文的目的是介绍项目中使用到主要质量指标,这些质量指标可以分为以下三类: 质量保证过程指标生产事故管理指标度量质量文化指标 质量保证过程指标 质量保证指标可以通过测试覆盖率来度量功能和非功能测试的覆盖率,同时也可以根据测试发现…...

6.12作业
1、pinia和vuex的区别 1.pinia没有mutations,只有state,getters,actions 2.pinia分模块不需要modules (之前vuex分模块需要modules) 3.pinia体积更小(性能更好) 4.pinia可以直接修改state数据 2、Vue2和vue3的响应式原理分别是什么&#x…...
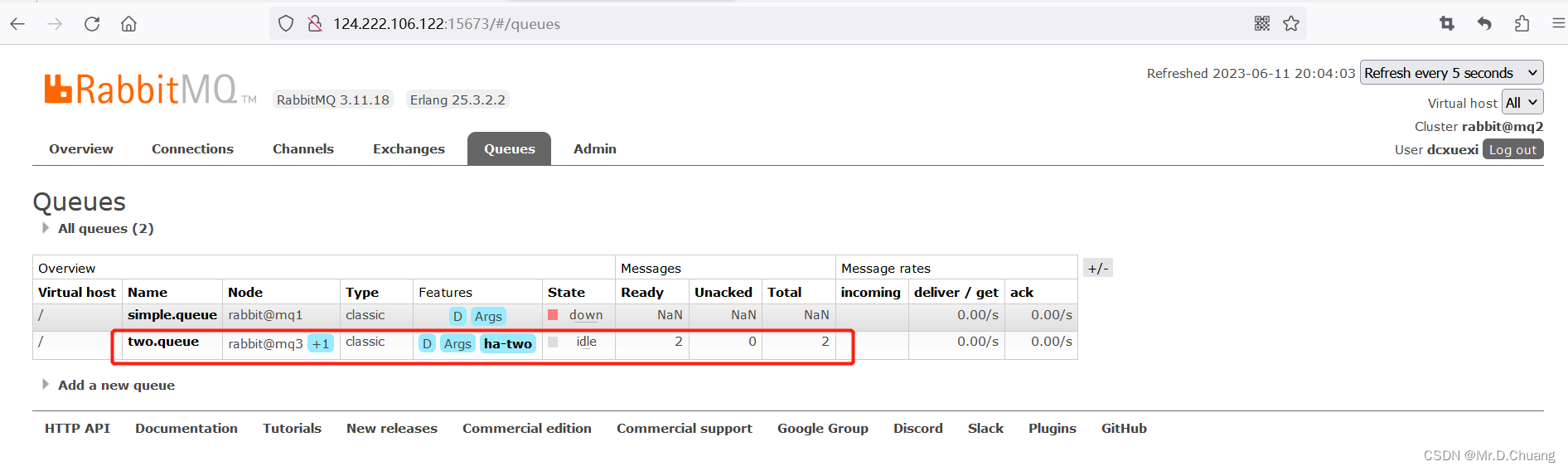
RabbitMQ集群部署之镜像模式
RabbitMQ集群的普通模式中,一旦创建队列的主机宕机,队列就会不可用。不具备高可用能力。如果要解决这个问题,必须使用官方提供的镜像集群方案。 官方文档地址:https://www.rabbitmq.com/ha.html 1.镜像模式的特征 默认情况下&a…...

【算法】Remove Zero Sum Consecutive Nodes from Linked List 从链表中删去总和值为零的连续节点
文章目录 Remove Zero Sum Consecutive Nodes from Linked List 从链表中删去总和值为零的连续节点问题描述:分析代码 Remove Zero Sum Consecutive Nodes from Linked List 从链表中删去总和值为零的连续节点 问题描述: 给你一个链表的头节点 head&am…...
音悦台项目测试报告
文章目录 项目背景项目功能测试计划与设计功能测试自动化测试 测试结果功能测试结果UI自动化测试结果 项目背景 现如今人们的生活压力大,容易使人疲惫,为了使得人们在闲暇之余可以听音乐放松,为此设计出一款轻量的听音乐网站,快速…...

数据库存储过程和函数
MySQL存储过程和存储函数 MySQL中提供存储过程(procedure)与存储函数(function)机制,我们先将其统称为存储程序,一般的SQL语句需要先编译然后执行,存储程序是一组为了完成特定功能的SQL语句集&…...

Spring依赖注入有哪些?各有什么优缺点?
文章目录 前言概述一、属性注入1.1 实例1.2 优点1.3 缺点 二、Setter注入2.1 实例2.2 优点2.3 缺点 三、 构造方法注入3.1 实例3.2 优点3.3 缺点 四、扩展 前言 IoC和DI是Spring中重要的两个概念,其中IoC指的是控制反转,DI(依赖注入)指的是IoC的具体实现…...
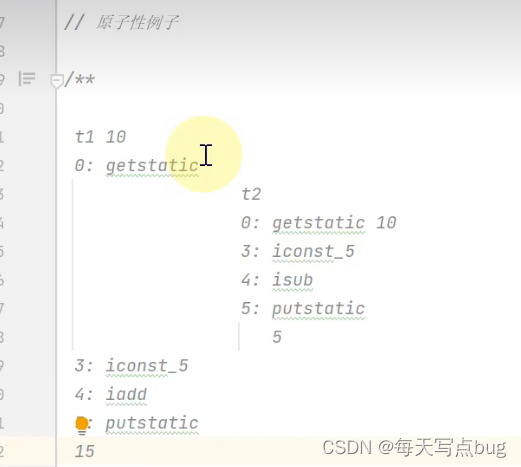
java八股文-并发篇
并发篇 1. 线程状态 要求 掌握 Java 线程六种状态掌握 Java 线程状态转换能理解五种状态与六种状态两种说法的区别 六种状态及转换 分别是 新建 当一个线程对象被创建,但还未调用 start 方法时处于新建状态此时未与操作系统底层线程关联 可运行 调用了 start …...

Elasticsearch8.6.0安装
Elasticsearch 8.5.0 安装 Elasticsearch 简介Elasticsearch 8.6.0 安装创建网络拉取镜像运行镜像设置密码修改kibana配置绑定ES代码绑定:手动绑定: 配置ik分词器扩展词词典停用词词典 Elasticsearch 简介 Elasticsearch(ES) 是一…...

Vue - 第五天 动态组件 插槽 自定义指令
动态组件& 插槽& 自定义指令 一、动态组件1.什么是动态组件2.如何实现动态组件渲染3.使用 keep-alive 保持状态4. keep-alive 对应的生命周期函数5. keep-alive 的 include 属性6.动态展示左右组件7.例子 二、插槽1.什么是插槽2.体验插槽的基础用法2.1 没有预留插槽的内…...

如何开展web自动化测试
Web 自动化是指使用测试脚本在 Web 上自动执行任务。它包括填写表单、导航网页、单击链接或按钮以及从网站中提取数据等任务。 它可用于各种目的,例如自动输入数据或测试网站的功能。有几种工具和编程语言可用于自动化网络上的任务,包括Selenium&#x…...

【博学谷学习记录】超强总结,用心分享 | 架构师 Maven学习总结
文章目录 Maven基本1.什么是Maven2.为什么用Maven?(1)jar 包的规模(2) jar 包的来源(3)jar 包之间的依赖关系 3.Maven目录结构4.maven仓库配置 Pom层次Pom文件简介Super POM 依赖管理1 依赖传递2 传递性依…...
PPT里文字太多如何排版-一口气教你7种布局瞬间让PPT高大上起来
简介 这是我们学PPT处于初级到中级进化阶段常做的一件事,就是拿了这种纯文字类版面来做布局。而且这种文字都是政企类的、相当苦涩难懂、无法创意。 因此我们会要求使用7种排版来优化这个版面。这和达芳奇画鸡蛋很像,这样的练习需要坚持一段时间,就是拿了纯文字来beautifu…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...
