2.4 逻辑代数的基本定理

学习目标:
如果我要学习逻辑代数的基本定理,我会采取以下步骤:
1. 学习基本概念:首先,我会花时间了解逻辑代数的基本概念,如逻辑运算符(合取、析取、否定等)、真值表、逻辑等价性等。这将帮助我建立对逻辑代数的整体认识。
2. 研究基本定理:我会仔细研究逻辑代数的基本定理,如结合律、分配律、吸收律、德摩根定律等。对于每个定理,我将理解其定义、表述和推理规则。我可以参考教科书、学术论文、在线课程等资源来深入了解每个定理的证明和应用。
3. 推导演练:为了更好地理解和应用基本定理,我会进行推导演练。我会选择一些具体的逻辑表达式或问题,并尝试使用基本定理来简化表达式、推导等价关系或解决问题。这样的练习有助于我加深对基本定理的理解和掌握。
4. 解决实际问题:逻辑代数的基本定理不仅仅是理论性的,它们在解决实际问题中也具有应用。我会寻找实际生活中的例子,将逻辑代数的基本定理应用于解决问题,例如电路设计、布尔函数简化等。通过实际问题的应用,我可以更好地理解基本定理的实际意义和应用领域。
5. 深入学习高级定理:一旦我对逻辑代数的基本定理有了扎实的理解,我可以进一步研究和学习高级定理。这些高级定理可能包括完备性定理、布尔代数的完备性等,它们在逻辑代数的更深层次理论和应用中发挥重要作用。
6. 练习和交流:学习逻辑代数的基本定理需要大量的练习和实践。我会寻找习题集、在线练习平台或参与学习群体,与其他人交流和讨论,以提高我的技能和应用能力。
总的来说,学习逻辑代数的基本定理需要耐心和实践。通过理论学习、推导演练、解决实际问题以及与他人交流,我相信我可以更好地掌握逻辑代数的基本定理,并将其应用于实际问题中。

2.4.1 代入定理
在逻辑代数中,代入定理是一个重要的概念。它描述了在逻辑表达式中进行替换的一种规则。代入定理允许我们在一个逻辑表达式中用一个变量的替代物替换另一个变量,而不改变表达式的逻辑等价性。
代入定理可以用以下形式表示:
如果在一个逻辑表达式中,我们将一个变量A替换为一个逻辑表达式B,并且将该表达式中所有出现的A都替换为B,则结果表达式与原始表达式是逻辑等价的。
换句话说,代入定理允许我们在逻辑表达式中进行变量的替换,而不改变表达式的真值。
例如,考虑以下逻辑表达式:
P ∧ Q
我们可以使用代入定理将P替换为R ∨ S,得到:
(R ∨ S) ∧ Q
这两个表达式在逻辑上是等价的,因为它们具有相同的真值。
代入定理在逻辑推理和证明过程中非常有用。它允许我们在逻辑表达式中引入更复杂的子表达式,从而扩展我们的推理能力。通过使用代入定理,我们可以将问题分解为更简单的部分,并且能够进行更深入的逻辑推理。

2.4.2 反演定理
在逻辑代数中,反演定理(Inverse Law)是一种描述逻辑运算的规律。它表明在逻辑运算中,如果我们对一个操作进行两次,就会回到初始状态。反演定理在逻辑等式的证明和简化过程中经常被使用。
在逻辑代数中,通常有两种基本的逻辑运算:合取(AND)和析取(OR)。反演定理针对这两种运算有不同的表达形式:
1. 合取的反演定理:
如果我们对一个合取操作进行两次,结果与原始操作相同。即:
P ∧ (P ∧ Q) ≡ P
这个定理表明,如果一个命题与它自身和另一个命题进行合取运算,结果等价于仅考虑第一个命题。
2. 析取的反演定理:
如果我们对一个析取操作进行两次,结果与原始操作相同。即:
P ∨ (P ∨ Q) ≡ P
这个定理表明,如果一个命题与它自身和另一个命题进行析取运算,结果等价于仅考虑第一个命题。
反演定理可以用来简化逻辑表达式,消除多余的逻辑运算符,以及在证明过程中推导等价关系。它提供了一种有效的方法来处理逻辑表达式中的重复运算,使得逻辑推理更加简洁和直观。
需要注意的是,反演定理只适用于相同的操作符。对于不同的逻辑运算符,如合取和析取的反演定理是不成立的。
总之,反演定理是逻辑代数中的一种重要规律,它描述了对一个操作进行两次会回到初始状态的性质。在逻辑等式的简化和证明过程中,反演定理可以帮助我们简化逻辑表达式,减少冗余,并提供更清晰的推理步骤。
2.4.3 对偶定理:
对偶定理(Duality Law)是逻辑代数中的一个基本原理,它描述了逻辑运算之间的对称性。对偶定理表明,在逻辑运算中,通过对运算符和操作数进行互换,可以得到一个与原始运算等价的新运算。
在逻辑代数中,常见的逻辑运算包括合取(AND)、析取(OR)、否定(NOT)等。对于这些运算,对偶定理可以被表述为以下形式:
1. 合取与析取的对偶定理:
如果我们将合取运算(∧)替换为析取运算(∨),将析取运算(∨)替换为合取运算(∧),并且对操作数进行否定(取反),则等式仍然成立。即:
¬(P ∧ Q) ≡ ¬P ∨ ¬Q
¬(P ∨ Q) ≡ ¬P ∧ ¬Q
这意味着,通过对合取和析取运算符进行互换,并对操作数取反,我们可以得到一个等价的逻辑表达式。
2. 否定的对偶定理:
如果我们将否定运算(NOT)应用两次于同一个命题,等价于不对该命题进行任何操作。即:
¬(¬P) ≡ P
这表示对一个命题进行两次否定运算等价于不对该命题进行任何否定操作。
对偶定理在逻辑等式的证明和简化过程中经常被使用。它允许我们通过运算符和操作数的对换来推导等价的逻辑表达式,从而简化复杂的逻辑等式。通过应用对偶定理,我们可以转换逻辑运算的形式,得到更容易理解和处理的表达式。
需要注意的是,对偶定理是在逻辑运算之间进行对称性的变换,而不是针对逻辑运算的真值。也就是说,对偶定理保持逻辑等价性,但不一定保持真值的一致性。
总之,对偶定理是逻辑代数中的一个重要原理,它描述了逻辑运算之间的对称性。通过对运算符和操作数进行互换,我们可以得到一个与原始运算等价的新运算。对偶定理在逻辑等式的简化和证明过程中发挥着重要的作用。
总结:
上述三个定理中的重点、难点和易错点如下:
1. 合取与析取的对偶定理:
- 重点:理解合取和析取运算符之间的对称性,并且能够正确地应用对偶定理进行变换。
- 难点:在应用对偶定理时,需要小心操作数的取反,并确保运算符的互换是正确的。
- 易错点:混淆或错误地使用了取反操作符,导致结果不正确。忽略或错误地互换了合取和析取运算符。
2. 否定的对偶定理:
- 重点:理解对偶定理中否定运算的性质,即对一个命题进行两次否定运算等价于不进行任何否定操作。
- 难点:注意否定运算的应用顺序和次数,以确保正确地应用对偶定理。
- 易错点:错误地计算或应用否定运算,导致结果不正确。忽略了对偶定理中否定运算的特性。
3. 代入定理:
- 重点:理解代入定理的规则,即在一个逻辑表达式中用一个变量的替代物替换另一个变量,而不改变表达式的逻辑等价性。
- 难点:在应用代入定理时,确保替换变量的一致性和正确性,以及正确处理替换的范围。
- 易错点:错误地进行变量的替换或处理替换的范围,导致结果不正确。忽略了代入定理中逻辑等价性的要求。
对于这些定理,重要的是理解其定义、原理和应用规则,并通过练习和实践加深对其的掌握。在应用定理时,要特别注意操作的顺序、符号的正确使用和细节的准确性,以避免常见的易错点。反复练习和与他人的讨论也能帮助加深对这些定理的理解和运用能力。
相关文章:

2.4 逻辑代数的基本定理
学习目标: 如果我要学习逻辑代数的基本定理,我会采取以下步骤: 1. 学习基本概念:首先,我会花时间了解逻辑代数的基本概念,如逻辑运算符(合取、析取、否定等)、真值表、逻辑等价性等…...

适用于 Linux 的 Windows 子系统wsl文档
参考链接:https://learn.microsoft.com/zh-cn/windows/wsl/ 鸟哥的Linux私房菜:http://cn.linux.vbird.org/ http://cn.linux.vbird.org/linux_basic/linux_basic.php http://cn.linux.vbird.org/linux_server/ 目录 安装列出可用的 Linux 发行版列出已…...
C++特殊类的设计与类型转换
特殊类的设计与类型转换 特殊类的设计请设计一个类,只能在堆上创建对象请设计一个类,只能在栈上创建对象请设计一个类,只能创建一个对象(单例模式) C的类型转换 特殊类的设计 请设计一个类,只能在堆上创建对象 通过new创建的类就…...

如何通过关键词搜索API接口
如果你是一位电商运营者或者是想要进行1688平台产品调研的人员,你可能需要借助API接口来获取你所需要的信息。在这篇文章中,我们将会讨论如何通过关键词搜索API接口获取1688的商品详情。 第一步:获取API接口的授权信息 在使用API接口前&…...

智驾域控新战争打响,谁在抢跑?
智能驾驶域控制器赛道,已经成为了时下最为火热的市场焦点之一。 最近,头部Tier1均胜电子公布了全球首批基于高通Snapdragon Ride第二代芯片平台的智能驾驶域控制器产品nDriveH,在这一赛道中显得格外引人注意。 就在不久之前,均胜…...

Android 13无源码应用去掉无资源ID的按钮
Android Wifionly项目,客户要求去掉谷歌联系人里的 手机联系人按钮 需求分析 无应用源码,只能通过系统侧去修改 首先通过 Android Studio 工具 uiautomatorviewer 获取父控件资源ID chip_group ,然后通过遍历获取子控件去掉目标按钮 --- a/frameworks/base/core/java/andr…...
,正刊,SCIEEI双检,进化计算、模糊集和人工神经网络在数据不平衡中应用)
【SCI征稿】中科院2区(TOP),正刊,SCIEEI双检,进化计算、模糊集和人工神经网络在数据不平衡中应用
【期刊简介】IF:8.0-9.0,JCR1区,中科院2区(TOP) 【检索情况】SCIE&EI 双检,正刊 【数据库收录年份】2004年 【国人占比】22.78%(期刊国际化程度高) 【征稿领域】进化计算、模…...
)
Android Audio开发——AAudio基础(十五)
AAudio 是一个自 Android O 引入的新的 Android C API。它主要是为需要低延迟的高性能音频应用设计的。应用程序通过直接从流中读取或向流中写入数据来与 AAudio 通信,但它只包含基本的音频输入输出能力。 一、AAudio概述 AAudio 在应用程序和 Android 设备上的音频输入输出之…...
SDK接口远程调试【内网穿透】
文章目录 1.测试环境2.本地配置3. 内网穿透3.1 下载安装cpolar内网穿透3.2 创建隧道 4. 测试公网访问5. 配置固定二级子域名5.1 保留一个二级子域名5.2 配置二级子域名 6. 使用固定二级子域名进行访问 转发自cpolar内网穿透的文章:Java支付宝沙箱环境支付࿰…...

Mybatis学习笔记二
目录 一、MyBatis的各种查询功能1.1 查询一个实体类对象1.2 查询一个List集合1.3 查询单个数据1.4 查询一条数据为map集合1.5 查询多条数据为map集合1.5.1 方法一:1.5.2 方法二: 二、特殊SQL的执行2.1 模糊查询2.2 批量删除2.3 动态设置表名2.4 添加功能…...
大屏数据可视化开源项目
一、DataGear —— 数据可视化项目 官网:DataGear - 开源免费的数据可视化分析平台 DataGear 是一款开源免费的数据可视化分析平台,数据可视化看板。 功能特性: 1、多种数据源,支持运行时接入任意提供 JDBC 驱动的数据库&#…...

面试经典150题:数组/字符串合集
新专栏,预计两个月写完吧,每天下班回来抽空做几道题。会把做题计划顺序记录下来,如果你有缘,刷到这个开篇序列,那就跟着文章去练题吧。初学者可以慢慢来 88. 合并两个有序数组 void merge(vector<int>& nums…...

Java源文件的执行过程
目录 1.JVM 2.字节码 3.Java源文件执行的过程 4.JIT(Just In Time Compilation) 5.AOT(Ahead Of Time Compilation) 6.AOT破坏Java动态性 7.编译型语言与解释型语言 8.Java-编译与解释并存的语言 9.Java和C的相同点与不同…...

10个ai算法常用库java版
今年ChatGPT 火了半年多,热度丝毫没有降下来。深度学习和 NLP 也重新回到了大家的视线中。有一些小伙伴问我,作为一名 Java 开发人员,如何入门人工智能,是时候拿出压箱底的私藏的学习AI的 Java 库来介绍给大家。 这些库和框架为机器学习、深度学习、自然语言处理等提供了广…...

怎么看服务器带宽大小 103.219.179.X
第一种,可以使用网站测速,这种方式比较便捷,但是由于网站测速是测试服务器发送数据包到他网站节点的一个速度情况,有时候节点问题或者服务器做了封包限制可能导致测试不准确的情况。 第二种,可以在IIS上架设一个大一点…...
图形编辑器开发:最基础但却复杂的选择工具
大家好,我是前端西瓜哥。 对于一个图形设计软件,它最基础的工具是什么?选择工具。 但这个选择工具,却是相当的复杂。这次我来和各位,细说细说选择工具的一些弯弯道道。 我正在开发的图形设计工具的: http…...

apk签名-signapk.jar
如果做平台app开发,需要签platform签名,除了通过adroid.bp或者android.mk的方式使用AOSP整个大工程中签名外,还可以直接通过signapk.jar的方式进行签名,效率更高更快捷简便。 首先我们来回顾下AOSP平台签名的办法。 Android.mk 使…...
【100个高大尚求职简历】简历模板+修改教程+行业分类简历模板 (涵盖各种行业) (简历模板+编辑指导+修改教程)
文章目录 1 简历预览2 简历下载 很多人说自己明明投了很多公司的简历,但是都没有得到面试邀请的机会。自己工作履历挺好的,但是为什么投自己感兴趣公司的简历,都没有面试邀请的机会。反而是那些自己没有投递的公司,经常给自己打电…...

Nginx平滑升级版本或添加模块
文章目录 一、Nginx 平滑升级二、升级失败 回滚操作三、遇到问题 一、Nginx 平滑升级 一般有两种情况下需要升级 nginx,一种是确实要升级 nginx 的版本,另一种是要为 nginx 添加新的模块。 Nginx平滑升级其原理简单概括: (1&am…...
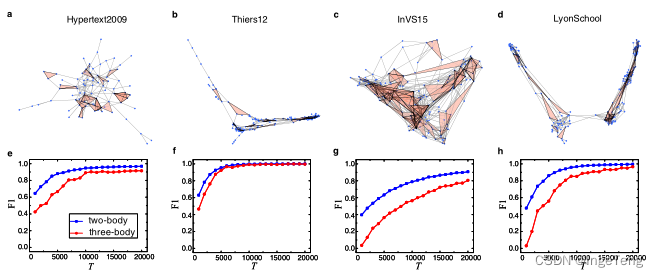
高阶复杂网络重建:从时间序列中重建高阶网络
论文链接:https://www.nature.com/articles/s41467-022-30706-9 一、为什么要研究高阶网络? 复杂网络跟我们生活息息相关,例如社交网络的信息传播,疾病的感染扩散和基因调控网络的相互作用等。越来越多的研究突破了传统网络中两…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...
