高阶复杂网络重建:从时间序列中重建高阶网络

论文链接:https://www.nature.com/articles/s41467-022-30706-9
一、为什么要研究高阶网络?
复杂网络跟我们生活息息相关,例如社交网络的信息传播,疾病的感染扩散和基因调控网络的相互作用等。越来越多的研究突破了传统网络中两个节点之间成对的关系,研究三个,四个甚至更多节点之间的高阶关系。例如,科学家合作发表论文,成对的连接只能描述两个作者的合作,却无法表示多个作者的情况。这些高阶关系在社会、信息和生物的网络中是客观存在且重要的,但是我们很难直接获取这样的高阶结构,往往依靠观测数据来重建复杂网络中的高阶关系。
二、文章动机:
现有方法是从简单网络或是成对节点的观测中重建出网络中的高阶关系。时间序列作为复杂系统中的原始观测数据,是网络重建任务中不可忽略的。同时,直接从时间序列中重建高阶网络,是对复杂系统的推理建模,是具有挑战的任务。
今天介绍的这篇文章从二元时间序列中重构单纯复形(高阶网络结构),是具有代表性和开创性的工作。
关键词: 高阶网络,网络重构,时间序列,单纯复形
三、什么是单纯复形(Simplices)?


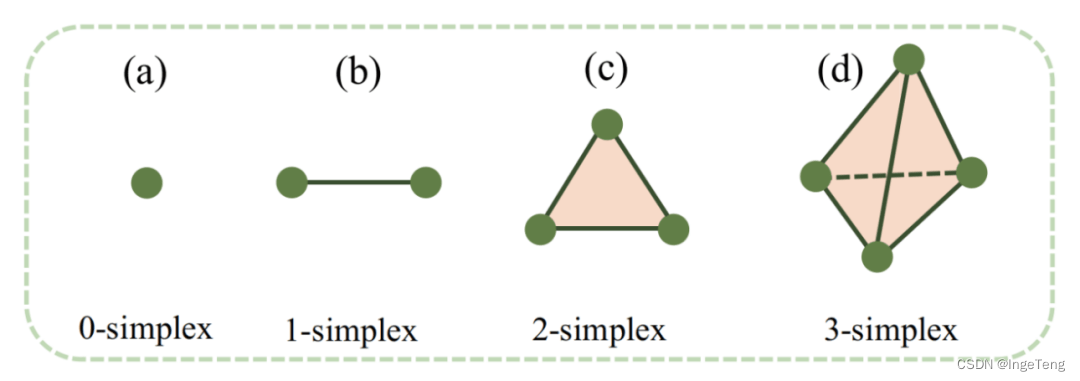
单纯复形是高阶网络的一种形式,它是由一系列单纯形组成的集合,有强大的数学形式做支撑,例如上图1(a) 为普通的网络连接,图1(b) 中黑色的边可以看做1-simplices,黄色的完整三角形可以看做2-simplices。在作者合作网络中,任意两个作者合作的关系,可以看做1-simplices,三个作者一起合作的关系组成2-simplices。当然,四人或是多人合作的关系为3-simplices或n-simplices,如下图所示。单纯复形突破了简单两两成对之间的关系,形成了高阶网络。
四、算法方法
本文从重构2-simplices网络出发,利用社会传染病传播模型和本文提出的Simplicial Ising动态模型生成考虑高阶信息的二元时间序列数据。
算法重构可以分为三个部分:
-
基于动力学模型生成的时序数据建立似然函数;
-
利用统计学方法(EM)重构网络连接概率;
-
2-step重构策略,优化提高框架效率。
算法框架细节如下:
1、建立似然函数
根据动力学生成的时序建立条件概率模型,个体 i 由其它单个个体 j 传染或激发的概率为:



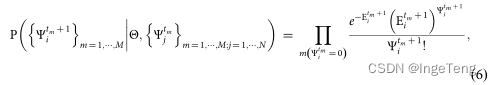
2、EM重构
建立基于最大似然估计的EM算法:
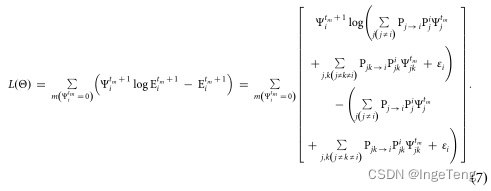


3、2-step策略
首先预测每一个个体(节点)的近似邻居,并提取预测邻居的时序,然后基于该数据重建出每个个体(节点)的两体和三体连接。该策略旨在保证精度的同时,减少计算时间。具体如图3所示

图3(a) 是基于2-simplices的高级动力学的网络,生成图b中的时间序列数据。根据上述介绍的算法,其中a->b->c->d->e 基于上述算法框架 1和 2,直接通过统计学方式计算每个连接的最大概率;a->b->f->h->h>i 为加入3 中的2-step策略的整体算法框架。
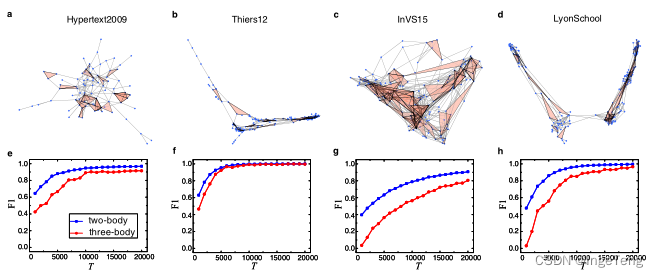
实验结果
为了验证算法框架的重建性能,本文基于两种高阶动力学数据(社会传染病传播和单纯形Ising动态),对3种人工合成的2-simplices(ERSC, SFSC, SWSC)和4个真实2-simplices(Hypertext2009, Thiers12, InVS15, LyonSchool)网络进行重建。

讨论
从实验可以看出该框架在合成2-simplices和真实2-simplices的鲁棒性和重建精度都很高,但是仍然存在一些限制。例如本文从二进制的时间序列中重建高阶网络,如何从实数或更一般的真实情形(数据缺失,噪声)重建高阶网络。并且本文对于时序的长度要求是较高的,如何从更短的时序中重建单纯复形或超图,都是后续有待研究的课题。
相关文章:

高阶复杂网络重建:从时间序列中重建高阶网络
论文链接:https://www.nature.com/articles/s41467-022-30706-9 一、为什么要研究高阶网络? 复杂网络跟我们生活息息相关,例如社交网络的信息传播,疾病的感染扩散和基因调控网络的相互作用等。越来越多的研究突破了传统网络中两…...
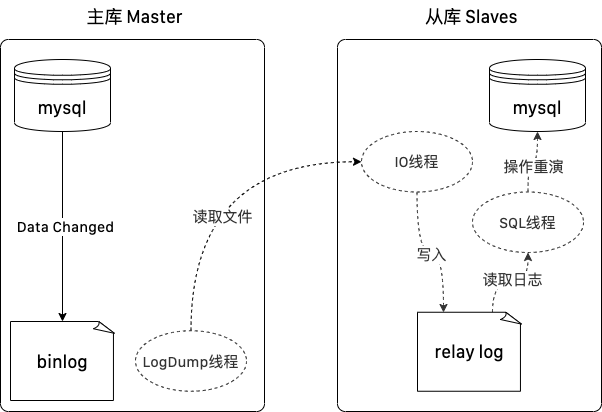
Day05 03-MySQL主从-主主原理与搭建详解
文章目录 第十六章 MySQL的系统架构(主从架构)16.1 MySQL集群架构的介绍16.1.1 主从架构介绍16.1.2 主从复制的原理 16.2 MySQL主从复制的实现16.2.1 环境说明16.2.2 主库配置16.2.3 从库配置16.2.4 主从复制测试 16.3 MySQL主主复制的实现16.3.1 主主复…...

STL之vector
目录 vector模拟实现一. vector的基本框架二. 常用方法及实现1.初始化和清理a. 默认构造函数b. 析构函数 2. 迭代器a. beginb. end 3.数据访问a. sizeb. capacityc. operator[]d. frontc. back 4.增删查改操作a. reserveb. resizec. insertd. push_backe. erasef. pop_back 5.构…...
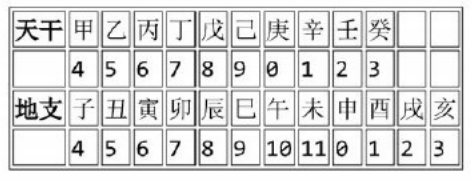
2020年CSP-J认证 CCF非专业级别软件能力认证第一轮真题-单项选择题解析
2020 CCF认证第一轮(CSP-J)真题 一、单项选择题 (共15题,每2分,共30分;每题有且有一个正确选项) 1、在内存储器中每个存储单元都被赋予一个唯一的序号,称为 A、下标 B、序号 C、地址 D、编号 答案:C…...
vscode Delete `␍⏎·····`
在公司拉取代码报错 Delete ␍⏎,首先问题的关键是换行导致,相信你看别的博客也知道为什么了,但是我使用别的博客的解决办法,没搞定,无论是配置 auto 还是命令行执行,都不行 下面介绍我的解决办法 我使用…...
读书笔记-《ON JAVA 中文版》-摘要16[第十六章 代码校验]
文章目录 第十六章 代码校验1. 测试1.1 单元测试1.2 JUnit1.3 测试覆盖率的幻觉 2. 前置条件2.1 断言(Assertions)2.2 Java 断言语法2.3 Guava 断言2.4 使用断言进行契约式设计2.4.1 检查指令2.4.2 前置条件2.4.3 后置条件2.4.4 不变性2.4.5 放松 DbC 检…...

SQL Server:打造高效数据管理系统的利器
使用SQL Server进行数据管理 简介 SQL Server是由Microsoft开发的一款关系型数据库管理系统,它可以用于存储和管理大量结构化数据。本篇博客将介绍如何使用SQL Server进行数据管理。 数据库连接 在开始使用SQL Server之前,需要先建立与数据库的连接。…...

代码随想录二刷day20 | 二叉树之 654.最大二叉树 617.合并二叉树 700.二叉搜索树中的搜索 98.验证二叉搜索树
day20 654.最大二叉树617.合并二叉树700.二叉搜索树中的搜索98.验证二叉搜索树 654.最大二叉树 题目链接 解题思路: 本题属于构造二叉树,需要使用前序遍历,因为先构造中间节点,然后递归构造左子树和右子树。 确定递归函数的参数…...

python基础知识(十三):numpy库的基本用法
目录 1. numpy的介绍2. numpy库产生矩阵2.1 numpy将列表转换成矩阵2.2 numpy创建矩阵 3. numpy的基础运算4. numpy的基础运算25. 索引 1. numpy的介绍 numpy库是numpy是python中基于数组对象的科学计算库。 2. numpy库产生矩阵 2.1 numpy将列表转换成矩阵 import numpy as …...
线程函数 tp_recv_thread() 源码分析)
【SA8295P 源码分析】16 - TouchScreen Panel (TP)线程函数 tp_recv_thread() 源码分析
【【SA8295P 源码分析】16 - TouchScreen Panel (TP)线程函数 tp_recv_thread 源码分析 一、TP 线程函数:tp_recv_thread()二、处理&上报 坐标数据 cypress_read_touch_data()系列文章汇总见:《【SA8295P 源码分析】00 - 系列文章链接汇总》 本文链接:《【SA8295P 源码…...
Python3数据分析与挖掘建模(13)复合分析-因子关分析与小结
1.因子分析 1.1 探索性因子分析 探索性因子分析(Exploratory Factor Analysis,EFA)是一种统计方法,用于分析观测变量之间的潜在结构和关联性。它旨在确定多个观测变量是否可以归结为较少数量的潜在因子,从而帮助简化…...
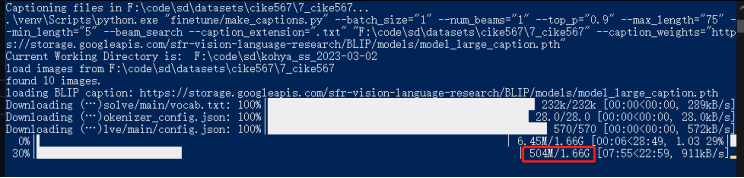
【stable diffusion】图片批量自动打标签、标签批量修改(BLIP、wd14)用于训练SD或者LORA模型
参考: B站教学视频【:AI绘画】新手向!Lora训练!训练集准备、tag心得、批量编辑、正则化准备】官方教程:https://github.com/darkstorm2150/sd-scripts/blob/main/docs/train_README-en.md#automatic-captioning 一、…...

TCP可靠数据传输
TCP的可靠数据传输 1.TCP保证可靠数据传输的方法 TCP主要提供了检验和、序号/确认号、超时重传、最大报文段长度、流量控制等方法实现了可靠数据传输。 检验和 通过检验和的方式,接收端可以检测出来数据是否有差错和异常,假如有差错就会直接丢失该TC…...

Python 私有变量和私有方法介绍
Python 私有变量和私有方法介绍 关于 Python 私有变量和私有方法,通常情况下,开发者可以在方法或属性名称前加上单下划线(_),以表示该方法或属性仅供内部使用,但这只是一种约定,并没有强制执行禁…...
Kotlin Lambda表达式和匿名函数的组合简直太强了
Kotlin Lambda表达式和匿名函数的组合简直太强了 简介 首先,在 Kotlin 中,函数是“第一公民”(First Class Citizen)。因此,它们可以被分配为变量的值,作为其他函数的参数传递或者函数的返回值。同样&…...

uniapp 小程序 获取手机号---通过前段获取
<template><!-- 获取手机号,登录内容 --><view><!-- 首先需要先登录获取code码,然后才可以获取用户唯一标识openid以及会话密钥及用于解密获取手机的加密信息 --><view click"login">登录</view><view…...

面板安全能力持续增强,新增日志审计功能,1Panel开源面板v1.3.0发布
2023年6月12日,现代化、开源的Linux服务器运维管理面板1Panel正式发布v1.3.0版本。 在这一版本中,1Panel进一步增强了安全方面的能力,包括新增SSH配置管理、域名绑定和IP授权支持,以及启用网站防盗链功能。此外,该版本…...
k8s学习-CKS考试必过宝典
目录 CKS考纲集群安装:10%集群强化:15%系统强化:15%微服务漏洞最小化:20%供应链安全:20%监控、日志记录和运行时安全:20% 报名模拟考试考试注意事项考前考中考后 参考 CKS考纲 集群安装:10% 使…...

jmeter如何将上一个请求的结果作为下一个请求的参数
目录 1、简介 2、用途 3、下载、简单应用 4、如何将上一个请求的结果作为下一个请求的参数 1、简介 在JMeter中,可以通过使用变量来将上一个请求的结果作为下一个请求的参数传递。 ApacheJMeter是Apache组织开发的基于Java的压力测试工具。用于对软件做压力测…...

JAVA如何学习爬虫呢?
学习Java爬虫需要掌握以下几个方面: Java基础知识:包括Java语法、面向对象编程、集合框架等。 网络编程:了解HTTP协议、Socket编程等。 HTML、CSS、JavaScript基础:了解网页的基本结构和样式,以及JavaScript的基本语…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...
