31-Golang中的二维数组
二维数组的使用方式
使用方式一:先声明/定义再赋值
- 1.语法:var数组名 [大小] [大小]类型
- 2.比如:var arr [2] [3]int,再赋值
package main
import ("fmt"
)func main() {//定义/声明数组var arr [4][6]int//赋初值arr[1][2] = 1arr[2][1] = 2arr[2][3] = 3for i := 0; i < 4 ; i++{for j := 0; j < 6; j++{fmt.Print(arr[i][j]," ")}fmt.Println()}
}
/*
0 0 0 0 0 0
0 0 1 0 0 0
0 2 0 3 0 0
0 0 0 0 0 0
*/
使用方式二:直接初始化
- 1.声明:var数组名[大小] [大小]类型 = [大小] [大小]类型{{初值…},{初值…}}
var arr[2][3]int = [2][3]int{{1,2,3},{4,5,6}}
fmt.Println("arr=", arr)
- 2.赋值(有默认值)
- 3.二维数组在声明/定义时也对应有四种写法[和一维数组类似]
- var数组名[大小] [大小]类型 = [大小] [大小]类型{{初值…},{初值…}}
- var数组名[大小] [大小]类型 = […] [大小]类型{{初值…},{初值…}}
- var数组名 = [大小] [大小]类型{{初值…},{初值…}}
- var数组名 = […] [大小]类型{{初值…},{初值…}}
二维数组在内存中的形式
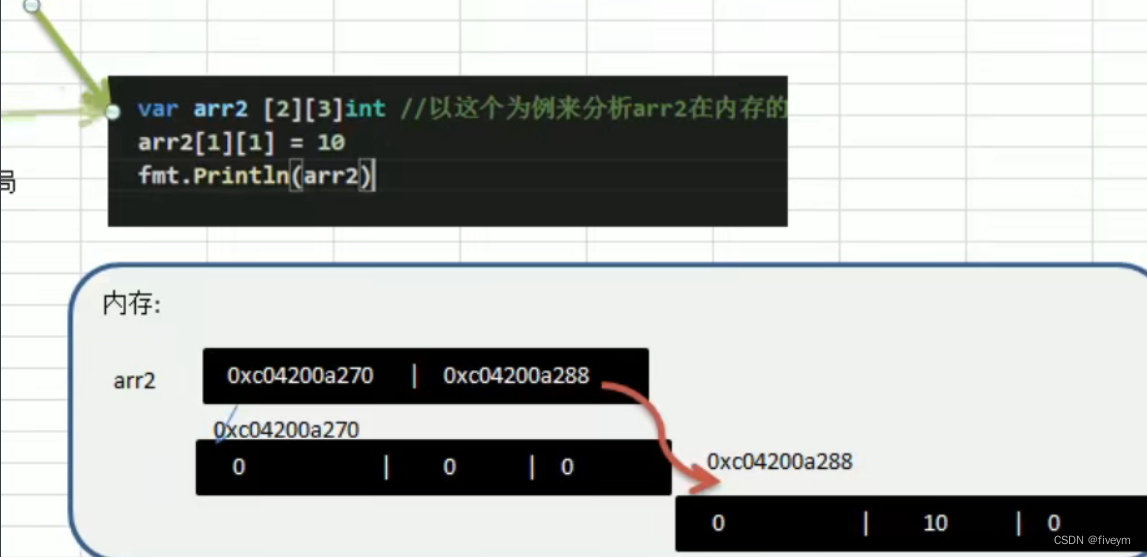
二维数组的遍历
双层for循环完成遍历
func main() {var arr = [2][3]int{{1,2,3},{4,5}}for i := 0; i < len(arr) ; i++{for j := 0; j < len(arr[i]); j++{fmt.Printf("%v\t", arr[i][j])}fmt.Println()}
}
/*
1 2 3
4 5 0
*/
for-range方式完成遍历
func main() {var arr = [2][3]int{{1,2,3},{4,5}}for i, v := range arr {for j, v1 := range v{fmt.Printf("arr[%v][%v]=%v\t",i,j,v1)}fmt.Println()}
}
/*
arr[0][0]=1 arr[0][1]=2 arr[0][2]=3
arr[1][0]=4 arr[1][1]=5 arr[1][2]=0
*/
案例
定义二维数组,用于保存三个班,每个班五名同学的成绩
并求出每个班级平均分,以及所有班级平均分
package main
import ("fmt")func main() {var scores [3][5]float64for i := 0; i < len(scores); i++{for j := 0; j < len(scores[i]); j++{fmt.Printf("请输入第%d班的第%d个学生的成绩\n", i + 1, j +1)fmt.Scanln(&scores[i][j])}}totalSum := 0.0for i := 0; i < len(scores); i++{sum := 0.0for j := 0; j < len(scores[i]); j++{sum += scores[i][j]}totalSum += sumfmt.Printf("第%d班的总分为%v,平均分为%v\n",i + 1,sum,sum/float64(len(scores[i])))}fmt.Printf("所有班的的总分为%v,平均分为%v",totalSum,totalSum/float64(len(scores)))
}/*
第1班的总分为36,平均分为7.2
第2班的总分为282,平均分为56.4
第3班的总分为137,平均分为27.4
所有班的的总分为455,平均分为151.66666666666666
*/相关文章:

31-Golang中的二维数组
二维数组的使用方式 使用方式一:先声明/定义再赋值 1.语法:var数组名 [大小] [大小]类型2.比如:var arr [2] [3]int,再赋值 package main import ("fmt" )func main() {//定义/声明数组var arr [4][6]int//赋初值arr[1][2] 1ar…...

<<Java开发环境配置>>6-SQLyog安装教程
一.SQLyog简介: SQLyog 是一个快速而简洁的图形化管理MySQL数据库的工具,它能够在任何地点有效地管理你的数据库,由业界著名的Webyog公司出品。使用SQLyog可以快速直观地让您从世界的任何角落通过网络来维护远端的MySQL数据库。 二.SQLyog下载: 下载地址…...

MySQL 中的 distinct 和 group by 哪个效率更高
先说大致的结论(完整结论在文末):在语义相同,有索引的情况下:group by和distinct都能使用索引,效率相同。在语义相同,无索引的情况下:distinct效率高于group by。原因是distinct 和 …...

计算机相关专业毕业论文选题推荐
计算机科学以下是我推荐的20个计算机科学专业的本科论文选题:基于机器学习的推荐算法研究与实现基于区块链技术的数字身份认证方案设计与实现基于深度学习的图像识别技术研究与应用基于虚拟现实技术的教育培训平台设计与实现基于物联网技术的智能家居系统研究与开发…...
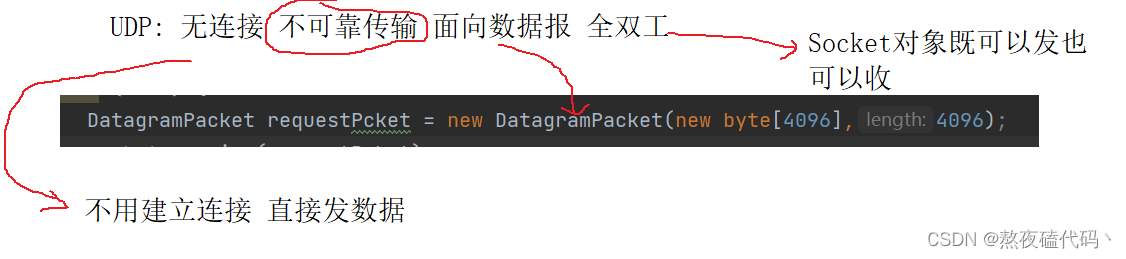
网络编程套接字之TCP
文章目录一、TCP流套接字编程ServerSocketSocketTCP长短连接二、TCP回显服务器客户端服务器客户端并发服务器UDP与TCP一、TCP流套接字编程 我们来一起学习一下TCP socket api的使用,这个api与我们之前学习的IO流操作紧密相关,如果对IO流还不太熟悉的&am…...

网络与串口调试工具TCPCOM
TCPCOM,网络与串口二合一调试助手,将网络调试助手与串口调试助手合二为一,绿色软件,简单高效。【软件特色】 1. 支持中英文双语言,自动根据操作系统环境选择系统语言类型; 2. 支持ASCII/Hex发送,发送和接收…...
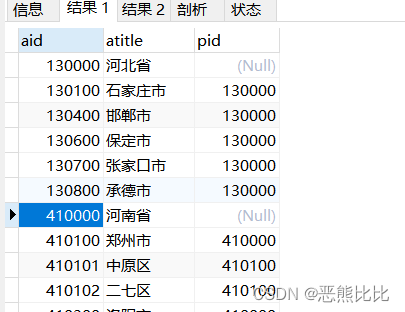
数据库常用命令
文章目录1. 数据库操作命令1.进入数据库2.查看数据库列表信息3.查看数据库中的数据表信息2.SQL语句命令1. 创建数据表2. 基本查询语句3. SQL排序4. SQL分组统计5. 分页查询6. 多表查询7.自关联查询8.子查询1. 数据库操作命令 1.进入数据库 mysql -uroot -p2.查看数据库列表信…...

PTA复习
函数 6-1 学生类的构造与析构 #include<bits/stdc.h> using namespace std; class Student {int num;string name;char sex; public:Student(int n,string nam,char s):num(n),name(nam),sex(s){cout<<"Constructor called."<<endl;}void display…...

TypeScript 学习之接口
接口:对值所具有的结构进行类型检查,称为“鸭式变型法”或“结构性子类型化” 基本使用 interface LabelledValue {label: string; }function printLabel(labelledObj: LabelledValue) {console.log(labelledObj.label); }let myObj {size: 10, label:…...

原码反码补码
在计算机中,负数都是以补码的形式存放的, 正数的原码、反码、补码完全一致。 原码:指的是正数的二进制或负数的二进制, 负数的二进制(原码),其实就是在正数的二进制的最高位前面加一个符号位 1。…...
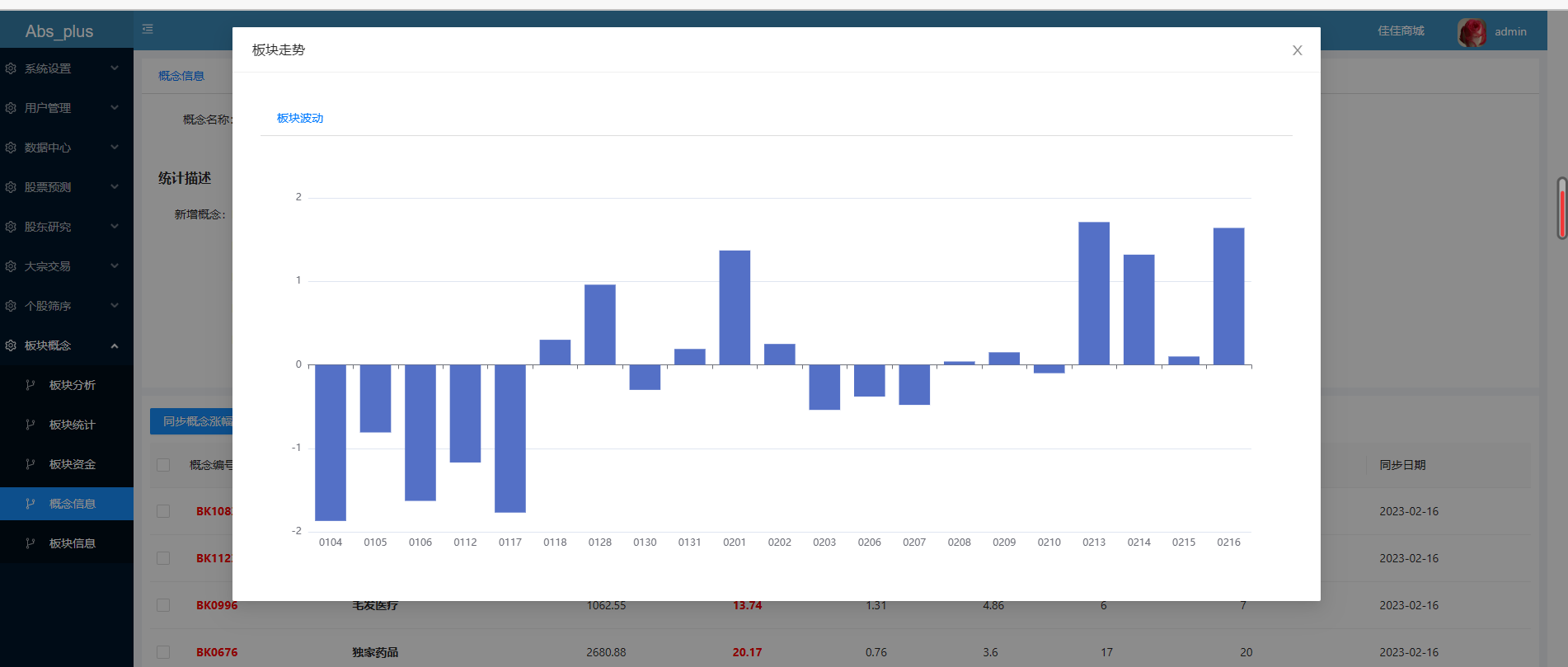
大数据选股智能推荐系统V1.0-1
很长时间没有发布博客了,这段时间个人确实有点忙。另外一方面在这段时间我也没有闲着。自己研发了一套大数据选股的智能推荐系统。废话不说,我们先来看这套系统:登录页面:(技术点:验证码的生成)…...

调研生成GIF表情包之路
调研阶段 gifshot.js合成GIF 可以从媒体流、视频或图像创建动画 GIF 的 JavaScript 库。 csdn地址:https://blog.csdn.net/qq_16494241/article/details/125717405 分解GIF图片、合成GIF图片 两步走: 1、分解GIF图片 libgif-js:JavaScrip…...

【RocketMQ】源码详解:生产者启动与消息发送流程
消息发送 生产者启动 入口 : org.apache.rocketmq.client.impl.producer.DefaultMQProducerImpl#start(boolean) 生产者在调用send()方法发送消息之前,需要调用start进行启动, 生产者启动过程中会启动一些服务和线程 启动过程中会启动MQClientInstance, 这个实例是针对一个项…...
信息安全(一)
思维导图 一、AES加解密 1.概述 1.1 概念 AES: 高级加密标准(Advanced Encryption Standard)是一种对称加密的区块加密标准。 (1)替代DES的新一代分组加密算法 (2)支持三种长度密钥&#x…...

企业多会场视频直播(主会场、分会场直播)实例效果
阿酷TONY 2023-2-16 长沙 活动直播做多会场切换功能(主会场、分会场、会场一、会场二、会场三自由切换) 企业多会场视频直播(主会场、分会场直播)实例效果 特点:支持PC端,也支持移动端观看,会…...
行列式)
线性代数速览(一)行列式
文章目录行列式🌻 行列式的定义🌼 行列式的性质🌷 一些定理🥀 行列式的计算🌺 克莱姆法则行列式 行列式的本质,就是一个数值。 🌻 行列式的定义 有三种定义:1、按行展开ÿ…...

恭喜山东翰林“智慧园区管理系统”获易知微可视化设计大赛二等奖
数字化经济发展是全球经济发展的重中之重,“数字孪生(Digital Twin)”这一词汇正在成为学术界和产业界的一个热点。数字孪生作为近年来的新兴技术,其与国民经济各产业融合不断深化,推动着各大产业数字化、网络化、智能…...

gulp简单使用
gulp gulp的核心理念是task runner 可以定义自己的一系列任务 等待任务被执行 基于文件stream的构建流 我们可以使用gulp的插件体系来完成某些任务 webpack的核心理念是module bundler webpack是一个模块化的打包工具 可以使用各种各样的loader来加载不同的模块 可以使用各种…...

ce认证机构如何选择?
CE认证想必大家都已经有所了解,它是产品进入欧盟销售的通行证,那么我们在办理CE认证时该怎么进行选择?带大家了解一下CE认证机构,以及该怎么去进行选择? 以下信息由证果果编辑整理,更多认证机构信息请到证果果网站查看。找机构…...

全网招募P图高手!阿里巴巴持续训练鉴假AI
P过的证件如何鉴定为真?三千万网友都晒出了与梅西的合影?图像编辑技术的普及让人人都能P图,但也带来“假图”识别难题,甚至是欺诈问题。 为此,阿里安全联合华中科技大学国家防伪工程中心、国际文档分析识别方向的唯一顶…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...
