Bernstein-Vazirani算法
B-V算法
(1) 问题描述
给定布尔函数f:{0,1}n→0,1f:{\left\{ {0,1} \right\}^n} \to{0,1}f:{0,1}n→0,1, 函数fff的值是由输入比特串xxx和确定的比特串sss做模2意义下的内积:f(x)=x⋅s(mod2),f\left( x \right) = x \cdot s\left( {\bmod 2} \right),f(x)=x⋅s(mod2),其中x⋅s=∑i(xi⊕si)x \cdot s = \sum\limits_i {\left( {{x_i} \oplus {s_i}} \right)} x⋅s=i∑(xi⊕si)
前提:可以调用访问函数fff的黑盒
问题:计算出比特串sss
经典意义下:
依次输入比特串xxx:
00...0000...0100...10...01...0010...00\begin{array}{l} 00...00\\ 00...01\\ 00...10\\ ...\\ 01...00\\ 10...00 \end{array}00...0000...0100...10...01...0010...00
对于第iii次输入:
000100...00→x⋅s(mod2)=si000100...00 \to x \cdot s\left( {\bmod 2} \right) = {s_i}000100...00→x⋅s(mod2)=si
重复该流程nnn次,即可确定比特串sss,上述方法的查询复杂度为O(n)O\left( n \right)O(n)
(2) 量子算法核心思路:
基础知识:H⊗n∣s⟩=12n2∑x(−1)s⋅x∣x⟩H^{\otimes n}|s\rangle=\frac{1}{2^{\frac{n}{2}}} \sum_{x}(-1)^{s \cdot x}|x\rangleH⊗n∣s⟩=22n1∑x(−1)s⋅x∣x⟩
Step1:制备初始量子比特∣Φ0⟩=∣0⟩⊗n\left| {{\Phi _0}} \right\rangle ={\left| 0 \right\rangle ^{ \otimes n}}∣Φ0⟩=∣0⟩⊗n
Step2:作用H⊗n{H^{ \otimes n}}H⊗n,得到量子态∣Φ0⟩=12n2∑x∣x⟩\left| {{\Phi _0}} \right\rangle = \frac{1}{{{2^{\frac{n}{2}}}}}\sum\limits_x {|x\rangle } ∣Φ0⟩=22n1x∑∣x⟩
Step3:作用量子黑盒Of{O_f}Of,Of:∣x⟩→(−1)x⋅s∣x⟩{O_f}:\left| x \right\rangle \to {\left( { - 1} \right)^{x \cdot s}}\left| x \right\rangleOf:∣x⟩→(−1)x⋅s∣x⟩,此时系统状态为∣Φ1⟩=12n2∑x(−1)s⋅x∣x⟩\left| {{\Phi _1}} \right\rangle = \frac{1}{{{2^{\frac{n}{2}}}}}\sum\limits_x {{{\left( { - 1} \right)}^{s \cdot x}}|x\rangle }∣Φ1⟩=22n1x∑(−1)s⋅x∣x⟩
Step4:作用H⊗n{H^{ \otimes n}}H⊗n,系统状态变为∣s⟩|s\rangle∣s⟩
此时测量量子系统即可得到比特串sss,该算法的查询复杂为O(1)O(1)O(1)
备注:上述量子黑盒OfO_fOf的实现方法与Deutsh算法相似,具体方法如下

(1) 制备量子态∣Ψ0⟩=∣0⟩n∣1⟩\left| {{\Psi _0}} \right\rangle = {\left| 0 \right\rangle ^n}\left| 1 \right\rangle∣Ψ0⟩=∣0⟩n∣1⟩
(2) 作用H⊗n{H^{ \otimes n}}H⊗n,量子系统变为∣Ψ1⟩=12n2∑x∣x⟩∣−⟩\left| {{\Psi _1}} \right\rangle = \frac{1}{{{2^{\frac{n}{2}}}}}\sum\limits_x {|x\rangle } \left| - \right\rangle∣Ψ1⟩=22n1x∑∣x⟩∣−⟩
(3) 作用Uf:∣x⟩∣y⟩→∣x⟩∣y⊕f(x)⟩U_f:\left|x\right\rangle\left|y\right\rangle \to\left|x\right\rangle\left|y\oplus f\left( x \right)\right\rangleUf:∣x⟩∣y⟩→∣x⟩∣y⊕f(x)⟩,量子系统演变为∣Ψ2⟩=12n2∑x∣x⟩1212(∣0⊕f(x)⟩−∣1⊕f(x)⟩)\left| {{\Psi _2}} \right\rangle = \frac{1}{{{2^{\frac{n}{2}}}}}\sum\limits_x {|x\rangle } \frac{1}{{{2^{\frac{1}{2}}}}}\left( {\left| {0 \oplus f\left( x \right)} \right\rangle - \left| {1 \oplus f\left( x \right)} \right\rangle } \right)∣Ψ2⟩=22n1x∑∣x⟩2211(∣0⊕f(x)⟩−∣1⊕f(x)⟩)
当f(x)=0{f\left( x \right)}=0f(x)=0时,∣x⟩1212(∣0⊕f(x)⟩−∣1⊕f(x)⟩)=∣x⟩1212(∣0⟩−∣1⟩)=∣x⟩∣−⟩\left|x\right\rangle \frac{1}{{{2^{\frac{1}{2}}}}}\left( {\left| {0 \oplus f\left( x \right)} \right\rangle - \left| {1 \oplus f\left( x \right)} \right\rangle } \right) = |x\rangle \frac{1}{{{2^{\frac{1}{2}}}}}\left( {\left| 0 \right\rangle - \left| 1 \right\rangle } \right) = |x\rangle \left| - \right\rangle∣x⟩2211(∣0⊕f(x)⟩−∣1⊕f(x)⟩)=∣x⟩2211(∣0⟩−∣1⟩)=∣x⟩∣−⟩
当f(x)=1{f\left( x \right)}=1f(x)=1时,∣x⟩1212(∣0⊕f(x)⟩−∣1⊕f(x)⟩)=∣x⟩1212(∣0⟩−∣1⟩)=−∣x⟩∣−⟩\left|x\right\rangle \frac{1}{{{2^{\frac{1}{2}}}}}\left( {\left| {0 \oplus f\left( x \right)} \right\rangle - \left| {1 \oplus f\left( x \right)} \right\rangle } \right) = |x\rangle \frac{1}{{{2^{\frac{1}{2}}}}}\left( {\left| 0 \right\rangle - \left| 1 \right\rangle } \right) = -|x\rangle \left| - \right\rangle∣x⟩2211(∣0⊕f(x)⟩−∣1⊕f(x)⟩)=∣x⟩2211(∣0⟩−∣1⟩)=−∣x⟩∣−⟩
不难发现UfU_fUf的作用为:∣x⟩∣−⟩→(−1)f(x)∣x⟩∣−⟩=(−1)s⋅x∣x⟩∣−⟩|x\rangle \left| - \right\rangle \to {\left( { - 1} \right)^{f\left( x \right)}}|x\rangle \left| - \right\rangle={\left( { - 1} \right)^{s \cdot x}}|x\rangle \left| - \right\rangle∣x⟩∣−⟩→(−1)f(x)∣x⟩∣−⟩=(−1)s⋅x∣x⟩∣−⟩
舍弃掉最后一个量子比特(辅助比特)∣−⟩\left| - \right\rangle∣−⟩,即实现了Step3中的黑盒OfO_fOf
参考资料
[1] Bernstein-Vazirani Algorithm 学习笔记
[2] 量子计算【算法篇】第7章 Deutsch-Josza算法及实现
(3) 由 Fourier Sampling 到 Deutsch-Jozsa Algorithm & Bernstein-Vazirani Algorithm
相关文章:

Bernstein-Vazirani算法
B-V算法 (1) 问题描述 给定布尔函数f:{0,1}n→0,1f:{\left\{ {0,1} \right\}^n} \to{0,1}f:{0,1}n→0,1, 函数fff的值是由输入比特串xxx和确定的比特串sss做模2意义下的内积:f(x)x⋅s(mod2),f\left( x \right) x \cdot s\left( {\bmod 2} \right),f(x)x⋅s(mod2),…...

华为OD机试 - 相对开音节 | 备考思路,刷题要点,答疑 【新解法】
最近更新的博客 【新解法】华为OD机试 - 关联子串 | 备考思路,刷题要点,答疑,od Base 提供【新解法】华为OD机试 - 停车场最大距离 | 备考思路,刷题要点,答疑,od Base 提供【新解法】华为OD机试 - 任务调度 | 备考思路,刷题要点,答疑,od Base 提供【新解法】华为OD机试…...
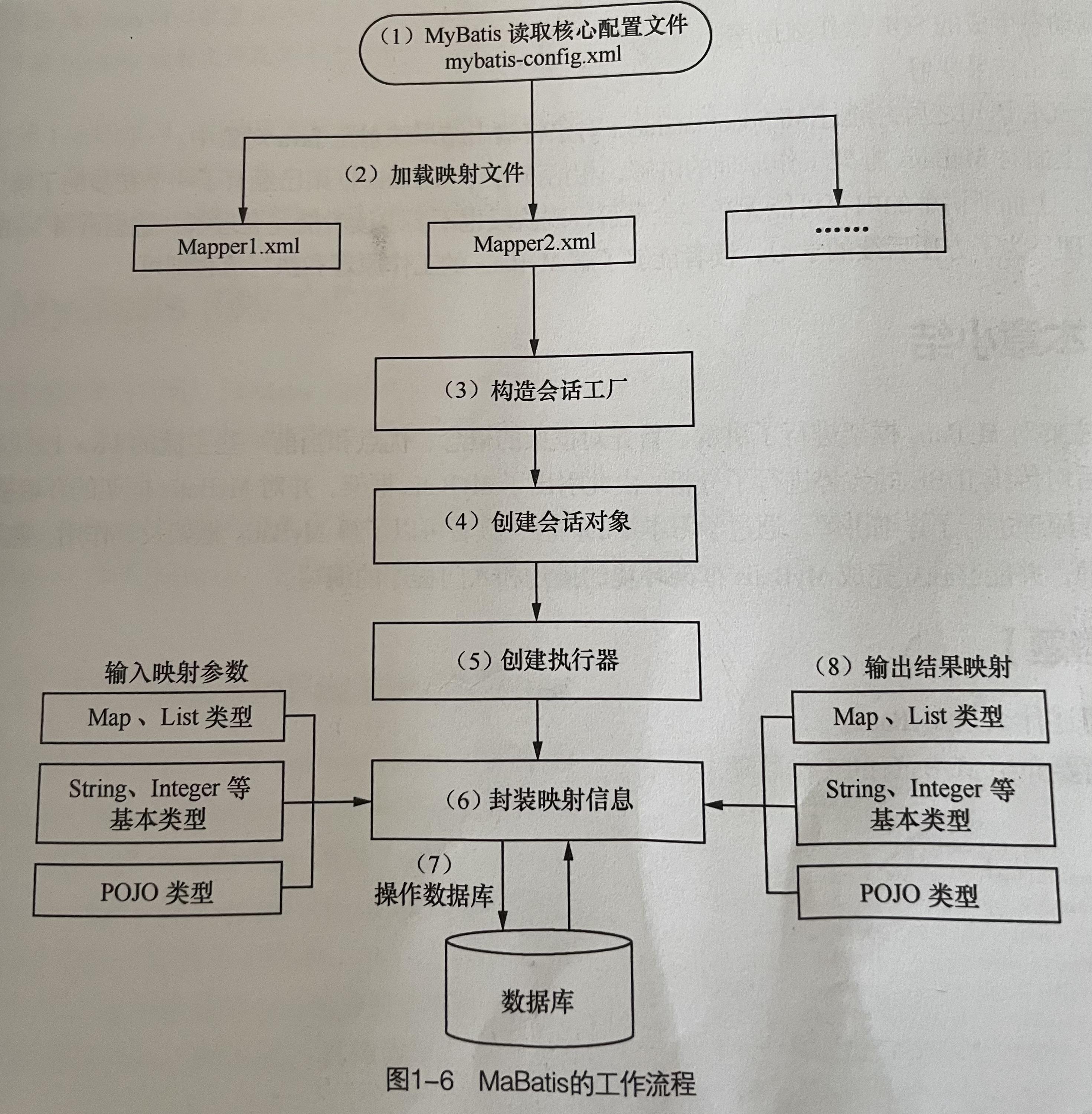
MyBatis
一、MyBatis环境搭建创建工程启动idea开发工具,选择工具栏中的“file”--“new”--“project”选项弹出“new project”对话框,编辑项目名称 选择maven项目,项目路径 单击 create 创建即可。引入相关依赖<dependencies><dependency&…...

良好的作息表
今天给大家带来“传说中”的“世界上最健康的作息时间表”(仅供参考),随时提醒自己吧,毕竟身体可是自己的哦。 7:30 起床:英国威斯敏斯特大学的研究人员发现,那些在早上5:22-7:21分起床的人,其血液中有一种能引起心脏病…...
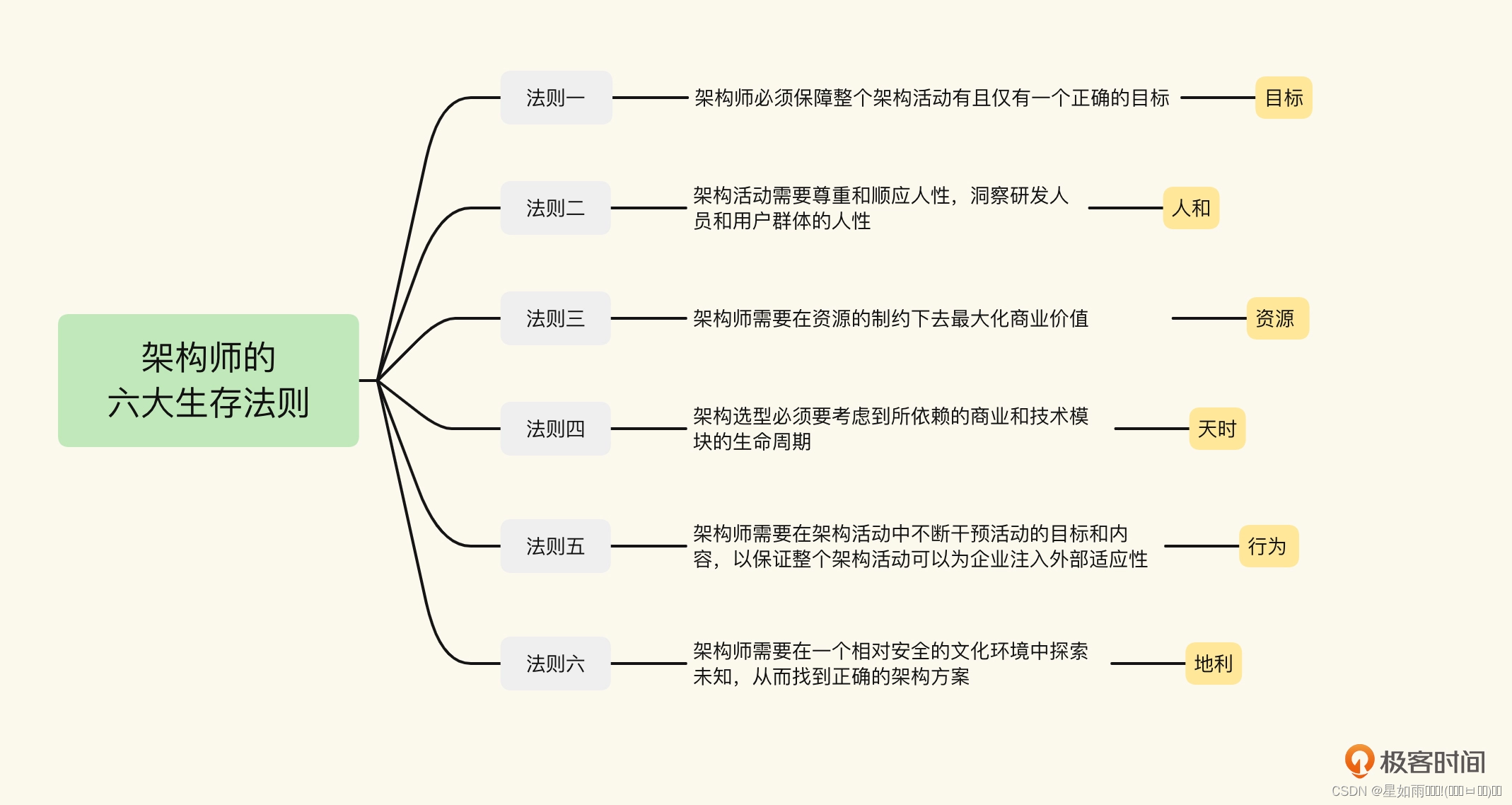
【郭东白架构课 模块一:生存法则】01|模块导学:是什么在影响架构活动的成败?
你好,我是郭东白。这节课是我们模块一的导入部分,我会先来介绍模块的主要内容,以及为什么我要讲生存法则这个话题。 一名软件架构师要为相对复杂的业务制定,并且引导实施一个结构化的软件方案。这个发现最终方案和推动实施的过程&…...

webshell免杀之函数与变量玩法
webshell免杀之函数与变量玩法 前言 前文列举了一些用符号免杀的例子,此篇文章就以函数和变量来尝试下免杀。 本文以PHP为例,用PHP中函数和变量及语法特性,在不隐藏函数关键字情况下进行免杀。 动态函数 PHP中支持一个功能叫 variable fu…...

【新解法】华为OD机试 - 去重求和 | 备考思路,刷题要点,答疑,od Base 提供
华为 OD 清单查看地址:blog.csdn.net/hihell/category_12199275.html 去重求和 | 备考思路,刷题要点,答疑,od Base 提供 给定一个数组,编写一个函数, 计算他的最大N个数和最小N个数的和, 需要对数组进行去重。 输入 第一行输入M,M表示数组大小 第二行输入M个数,表…...

MySQL 服务正在启动.MySQL 服务无法启动.服务没有报告任何错误。请键入 NET HELPMSG 3534 以获得更多的帮助。总结较全 (已解决)
输入以下命令启动mysql: net start mysql出现以下错误提示: MySQL 服务正在启动 .MySQL 服务无法启动。服务没有报告任何错误。请键入 NET HELPMSG 3534 以获得更多的帮助。 出现这个问题的话,一般有几个情况: 一、MySQL安装文…...

【数据结构与算法】数组2:双指针法 二分法(螺旋矩阵)
文章目录今日任务1.Leetcode977:有序数列的平方(1)题目(2)思路(3)暴力排序(4)双指针法2.Leetcode209:长度最小的子数组(1)题目&#x…...

librtmp优化
librtmp是一个RTMP的开源库,很多地方用它来做推流、拉流。它是RTMPDump开源软件里的一部分,librtmp的下载地址:RTMPDump,目前最新版是V2.3。本文重点介绍librtmp优化。 1、调整网络输出块大小。 RTMP_Connect0函数中LibRTMP是关…...

数据结构与算法(二):线性表
上一篇《数据结构与算法(一):概述》中介绍了数据结构的一些基本概念,并分别举例说明了算法的时间复杂度和空间复杂度的求解方法。这一篇主要介绍线性表。 一、基本概念 线性表是具有零个或多个数据元素的有限序列。线性表中数据…...
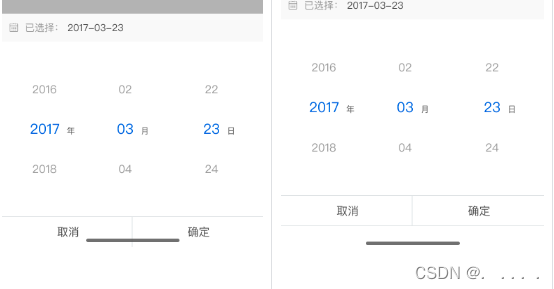
IOS安全区域适配
对于 iPhone 8 和以往的 iPhone,由于屏幕规规整整的矩形,安全区就是整块屏幕。但自从苹果手机 iphoneX 发布之后,前端人员在开发移动端Web页面时,得多注意一个对 IOS 所谓安全区域范围的适配。这其实说白了就是 iphoneX 之后的苹果…...
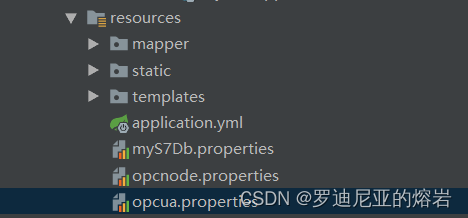
在Java 中 利用Milo通信库,实现OPCUA客户端,并生成证书
程序结构: 配置文件resources: opcua.properties 西门子PLC端口号为4840,kepserver为49320 #opcua服务端配置参数 #opcua.server.endpoint.urlopc.tcp://192.168.2.102:49320 opcua.server.endpoint.urlopc.tcp://192.168.2.11:4840 opcu…...

三分钟学会用Vim
Vim知识点 目录Vim知识点一:什么是vim二:vim常用的三种模式三:vim的基本操作一:什么是vim vim最小集 vim是一款多模式的编辑器—各种模式—每种模式的用法有差别—每种模式之间可以互相切换 但是我们最常用的就是3~5个模式 vi…...
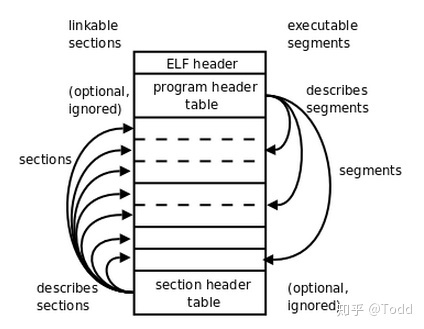
编译链接实战(8)认识elf文件格式
🎀 关于博主👇🏻👇🏻👇🏻 🥇 作者简介: 热衷于知识探索和分享的技术博主。 💂 csdn主页::【奇妙之二进制】 ✍️ 微信公众号:【Linux …...

新手小白如何入门黑客技术?
你是否对黑客技术感兴趣呢?感觉成为黑客是一件很酷的事。那么作为新手小白,我们该如何入门黑客技术,黑客技术又是学什么呢? 其实不管你想在哪个新的领域里有所收获,你需要考虑以下几个问题: 首先ÿ…...
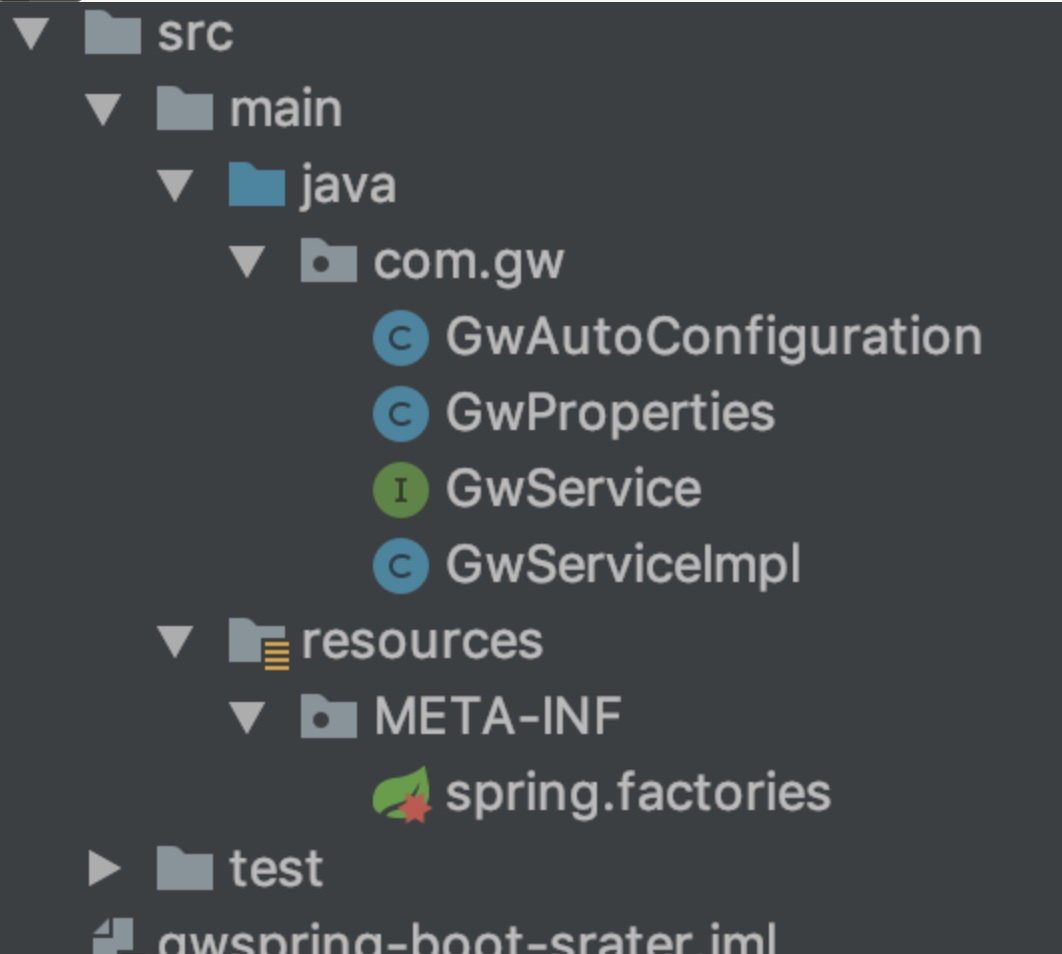
【java】Spring Boot --深入SpringBoot注解原理及使用
步骤一 首先,先看SpringBoot的主配置类: SpringBootApplication public class StartEurekaApplication {public static void main(String[] args){SpringApplication.run(StartEurekaApplication.class, args);} }步骤二 点进SpringBootApplication来…...
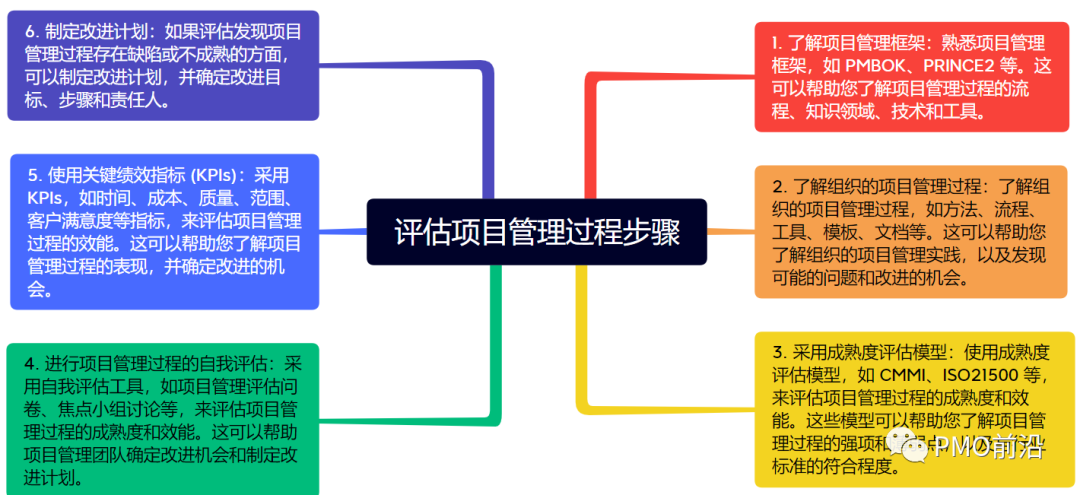
一文掌握如何对项目进行诊断?【步骤方法和工具】
作为项目经理和PMO,面对错综复杂的项目,需要对组织的项目运作情况进行精确的分析和诊断,找出组织项目管理中和项目运行中存在的问题和潜在隐患,分析其原因,预防风险,并且形成科学合理的决策建议和解决方案&…...

系统分析师真题2020试卷相关概念二
结构化设计相关内容: 结构化设计是一种面向数据流的系统设计方法,它以数据流图和数据字典等文档为基础。数据流图从数据传递和加工的角度,以图形化方式来表达系统的逻辑功能、数据在系统内部的逻辑流向和逻辑变换过程,是结构化系统分析方法的主要表达工具及用于表示软件模…...
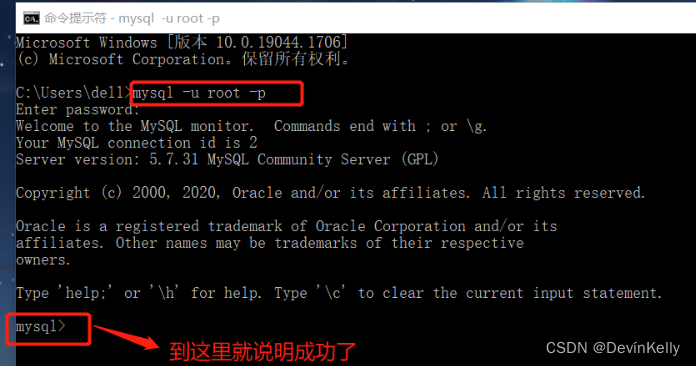
<<Java开发环境配置>>5-MySQL安装教程(绿色版)
一.MySQL绿色版安装: 1.直接解压下载的ZIP文件到对应的目录下(切记安装目录不要有中文); 如图:我的安装目录:D:Program Files 2.创建配置文件: 在MySQL安装目录下,创建一个my.ini配置文件,然后在里面添加以下内容(别忘了MySQL安装目录要改成…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

【iOS】 Block再学习
iOS Block再学习 文章目录 iOS Block再学习前言Block的三种类型__ NSGlobalBlock____ NSMallocBlock____ NSStackBlock__小结 Block底层分析Block的结构捕获自由变量捕获全局(静态)变量捕获静态变量__block修饰符forwarding指针 Block的copy时机block作为函数返回值将block赋给…...

负载均衡器》》LVS、Nginx、HAproxy 区别
虚拟主机 先4,后7...
