【1139. 最大的以 1 为边界的正方形】
来源:力扣(LeetCode)
描述:
给你一个由若干 0 和 1 组成的二维网格 grid,请你找出边界全部由 1 组成的最大 正方形 子网格,并返回该子网格中的元素数量。如果不存在,则返回 0。
示例 1:
输入:grid = [[1,1,1],[1,0,1],[1,1,1]]
输出:9
示例 2:
输入:grid = [[1,1,0,0]]
输出:1
提示:
- 1 <= grid.length <= 100
- 1 <= grid[0].length <= 100
- grid[i][j] 为 0 或 1
方法:动态规划
思路与算法
我们假设以 (x, y) 为右下方顶点的最大的正方形边长为 l,此时正方形的四个顶点分别为 (x − l + 1, y − l + 1), (x, y − l + 1), (x − l + 1, y), (x, y),此时需要保证正方形的四条边上的数字均为 1。我们设 left[x][y] 表示以 (x, y) 为起点左侧连续 1 的最大数目,right[x][y] 表示以 (x, y) 为起点右侧连续 1 的最大数目,up[x][y] 表示从 (x, y) 为起点上方连续 1 的最大数目,down[x][y] 表示以 (x, y) 为起点下方连续 1 的最大数目。此时正方形的四条边中以四个顶点为起点的连续 1 的数目分别为:上侧边中以 (x − l + 1, y − l + 1) 为起点连续 1 数目为 right[x − l + 1][y − l + 1],左侧边中以 (x − l + 1, y − l + 1) 为起点连续 1 的数目为 down[x − l + 1][y − l + 1],右侧边中以 (x, y) 为起点连续 1 的数目为 up[x][y],下侧边中以 (x,y) 为起点连续 1 的数目为 left[x][y]。
如果连续 1 的数目大于等于 l,则构成一条「合法」的边,如果正方形的四条边均「合法」,此时一定可以构成边界全为 1 且边长为 l 的正方形。

我们只需要求出以 (x, y) 为起点四个方向上连续 1 的数目,枚举边长 l 即可求出以 (x, y) 为右下顶点构成的边界为 1 的最大正方形,此时我们可以求出矩阵中边界为 1 的最大正方形。
本题即转换为求矩阵中任意位置 (x, y) 为起点上下左右四个方向连续 1 的最大数目,此时可以利用动态规划:
-
如果当前 grid[x][x] = 0 此时,四个方向的连续 1 的长度均为 0;
-
如果当前 grid[x][x] = 1 此时,四个方向的连续 1 的最大数目分别等于四个方向上前一个位置的最大数目加 1,计算公式如下:
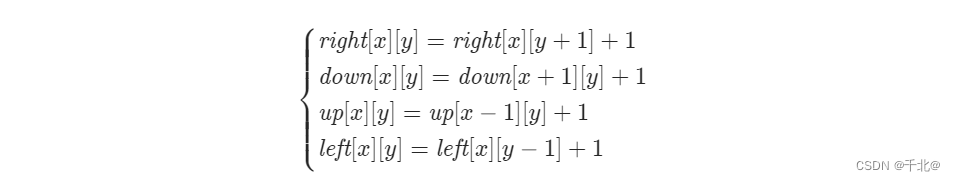
在实际计算过程中我们可以进行优化,不必全部计算出四个方向上的最大连续 1 的数目,可以进行如下优化:
只需要求出每个位置 (x, y) 为起点左侧连续 1 的最大数目 left[x][y] 与上方连续 1 的最大数目 up[x][y] 即可。假设当前正方形的边长为 l,此时只需检测 up[x][y], left[x][y], left[x − l + 1][y], up[x][y − l + 1] 是否均满足大于等于 l 即可检测正方形的合法性。
枚举正方形的边长时可以从大到小进行枚举,我们已经知道以 (x, y) 为起点左侧连续 1 的最大数目 left[x][y] 与上方连续 1 的最大数目 up[x][y],此时能够成正方形的边长的最大值一定不会超过二者中的最小值 min(left[x][y], up[x][y]),从大到小枚举直到可以构成“合法”的正方形即可。
代码:
class Solution {
public:int largest1BorderedSquare(vector<vector<int>>& grid) {int m = grid.size(), n = grid[0].size();vector<vector<int>> left(m + 1, vector<int>(n + 1));vector<vector<int>> up(m + 1, vector<int>(n + 1));int maxBorder = 0;for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {if (grid[i - 1][j - 1] == 1) {left[i][j] = left[i][j - 1] + 1;up[i][j] = up[i - 1][j] + 1;int border = min(left[i][j], up[i][j]);while (left[i - border + 1][j] < border || up[i][j - border + 1] < border) {border--;}maxBorder = max(maxBorder, border);}}}return maxBorder * maxBorder;}
};
执行用时:8 ms, 在所有 C++ 提交中击败了100.00%的用户
内存消耗:11.4 MB, 在所有 C++ 提交中击败了54.29%的用户
复杂度分析
时间复杂度:O(m × n × min(m, n)),其中 m 表示矩阵的行数,n 表示矩阵的列数。
空间复杂度:O(m × n),其中 m 表示矩阵的行数,n 表示矩阵的列数。需要保存矩阵中每个位置的最长连续 1 的数目,需要的空间为 O(m × n)。
author:LeetCode-Solution
相关文章:
【1139. 最大的以 1 为边界的正方形】
来源:力扣(LeetCode) 描述: 给你一个由若干 0 和 1 组成的二维网格 grid,请你找出边界全部由 1 组成的最大 正方形 子网格,并返回该子网格中的元素数量。如果不存在,则返回 0。 示例 1&#…...
windows11安装sqlserver2022报错
window11安装SQL Server 2022 报错 糟糕… 无法安装SQL Server (setup.exe)。此 SQL Server安装程序介质不支持此OS的语言,或没有SQL Server英语版本的安装文件。请使用匹配的特定语言SQL Server介质;或安装两个特定语言MUI,然后通过控制面板的区域设置…...

Python快速上手系列--日志模块--详解篇
前言本篇主要说说日志模块,在写自动化测试框架的时候我们就需要用到这个模块了,方便我们快速的定位错误,了解软件的运行情况,更加顺畅的调试程序。为什么要用到日志模块,直接print不就好了!那得写多少print…...

【THREE.JS学习(1)】绘制一个可以旋转、放缩的立方体
学习新技能,做一下笔记。在使用ThreeJS的时候,首先创建一个场景const scene new THREE.Scene();接着,创建一个相机其中,THREE.PerspectiveCamera()四个参数分别为:1.fov 相机视锥体竖直方向视野…...
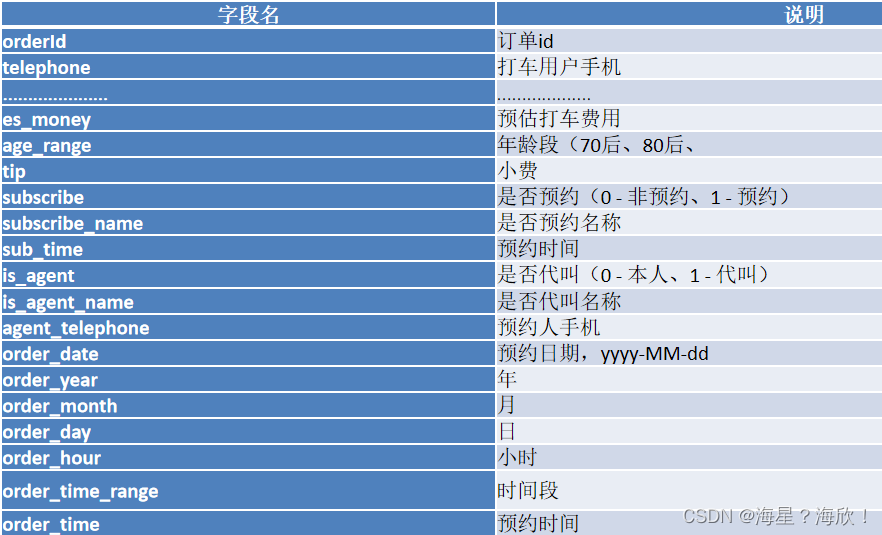
数仓实战 - 滴滴出行
项目大致流程: 1、项目业务背景 1.1 目的 本案例将某出行打车的日志数据来进行数据分析,例如:我们需要统计某一天订单量是多少、预约订单与非预约订单的占比是多少、不同时段订单占比等 数据海量 – 大数据 hive比MySQL慢很多 1.2 项目架…...
python虚拟环境与环境变量
一、环境变量 1.环境变量 在命令行下,使用可执行文件,需要来到可执行文件的路径下执行 如果在任意路径下执行可执行文件,能够有响应,就需要在环境变量配置 2.设置环境变量 用户变量:当前用户登录到系统,…...

BeautifulSoup文档4-详细方法 | 用什么方法对文档树进行搜索?
4-详细方法 | 用什么方法对文档树进行搜索?1 过滤器1.1 字符串1.2 正则表达式1.3 列表1.4 True1.5 可以自定义方法2 find_all()2.1 参数原型2.2 name参数2.3 keyword 参数2.4 string 参数2.5 limit 参数2.6 recursive 参数3 find()4 find_parents()和find_parent()5…...

初识Tkinter界面设计
目录 前言 一、初识Tkinter 二、Label控件 三、Button控件 四、Entry控件 前言 本文简单介绍如何使用Python创建一个界面。 一、初识Tk...

软件测试面试题中的sql题目你会做吗?
目录 1.学生表 2.一道SQL语句面试题,关于group by表内容: 3.表中有A B C三列,用SQL语句实现:当A列大于B列时选择A列否则选择B列,当B列大于C列时选择B列否则选择C列 4. 5.姓名:name 课程:subject 分数&…...

VS实用调试技巧
一.什么是BUG🐛Bug一词的原意是虫子,而在电脑系统或程序中隐藏着的一些未被发现的缺陷或问题,人们也叫它"bug"。这是为什么呢?这就要追溯到一个程序员与飞蛾的故事了。Bug的创始人格蕾丝赫柏(Grace Murray H…...
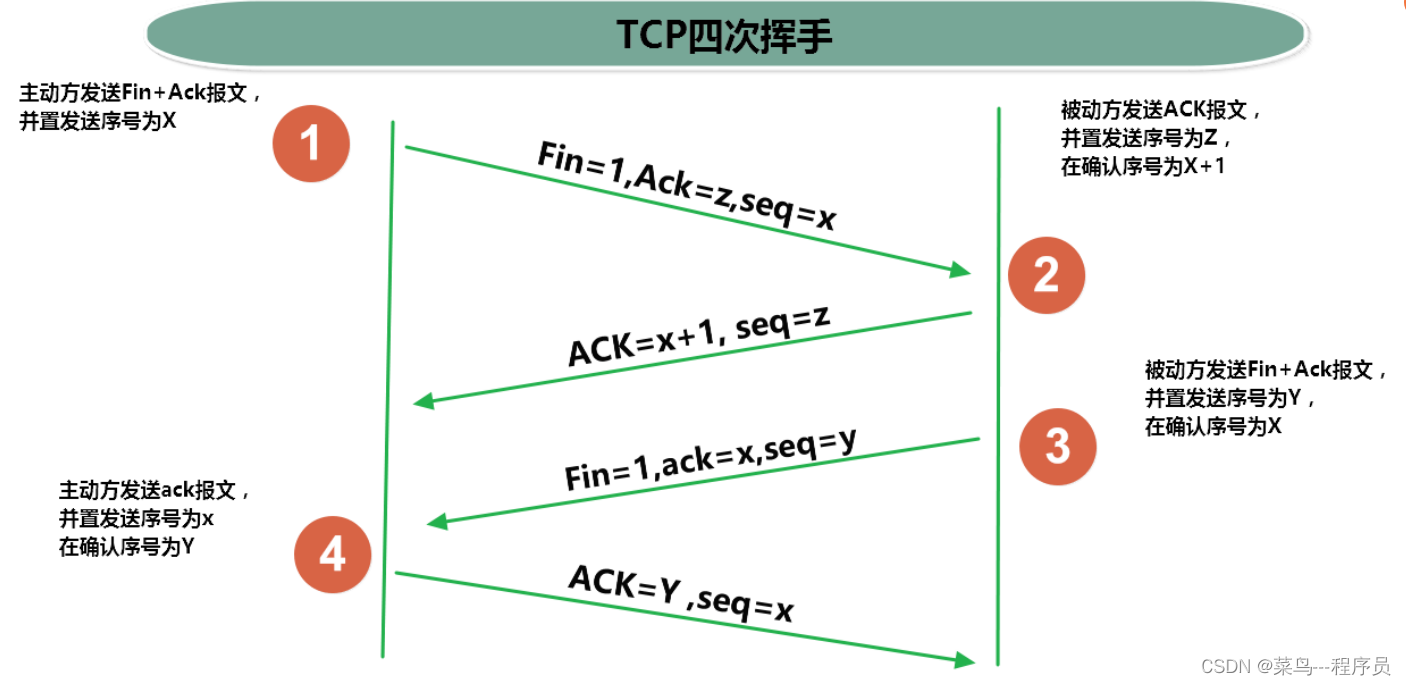
通俗易懂理解三次握手、四次挥手(TCP)
文章目录1、通俗语言理解1.1 三次握手1.2 四次挥手2、进一步理解三次握手和四次挥手2.1 三次握手2.2 四次挥手1、通俗语言理解 1.1 三次握手 C:客户端 S:服务器端 第一次握手: C:在吗?我要和你建立连接。 第二次握手ÿ…...
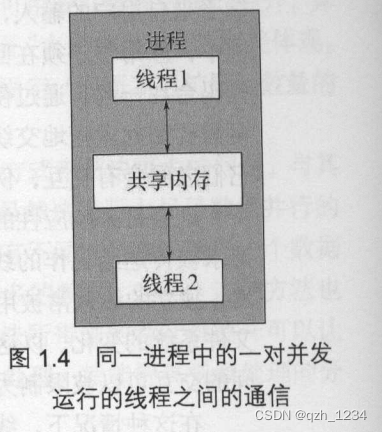
1.1 什么是并发
1.1 什么是并发 并发:指两个或更多独立的活动同时发生。并发在生活中随处可见。我们可以一边走路一边说话,也可以两只手同时做不同的动作。 1.1.1 计算机系统中的并发 当我们提到计算机术语的“并发”,指的是在单个系统里同时执行多个独立…...

万字讲解你写的代码是如何跑起来的?
今天我们来思考一个简单的问题,一个程序是如何在 Linux 上执行起来的? 我们就拿全宇宙最简单的 Hello World 程序来举例。 #include <stdio.h> int main() {printf("Hello, World!\n");return 0; } 我们在写完代码后,进行…...

034.Solidity入门——21不可变量
Solidity 中的不可变量是在编译时就被确定的常量,也称为常量变量(constant variable)或只读变量(read-only variable)。这些变量在定义时必须立即初始化,并且在整个合约中都无法被修改,可以在函…...
Vulnhub 渗透练习(四)—— Acid
环境搭建 环境下载 kail 和 靶机网络适配调成 Nat 模式,实在不行直接把网络适配还原默认值,再重试。 信息收集 主机扫描 没扫到,那可能端口很靠后,把所有端口全扫一遍。 发现 33447 端口。 扫描目录,没什么有用的…...

C++ 在线工具
online编译器https://godbolt.org/Online C Compiler - online editor (onlinegdb.com) https://www.onlinegdb.com/online_c_compilerC Shell (cpp.sh) https://cpp.sh/在线文档Open Standards (open-std.org)Index of /afs/cs.cmu.edu/academic/class/15211/spring.96/wwwC P…...

使用MMDetection进行目标检测、实例和全景分割
MMDetection 是一个基于 PyTorch 的目标检测开源工具箱,它是 OpenMMLab 项目的一部分。包含以下主要特性: 支持三个任务 目标检测(Object Detection)是指分类并定位图片中物体的任务实例分割(Instance Segmentation&a…...
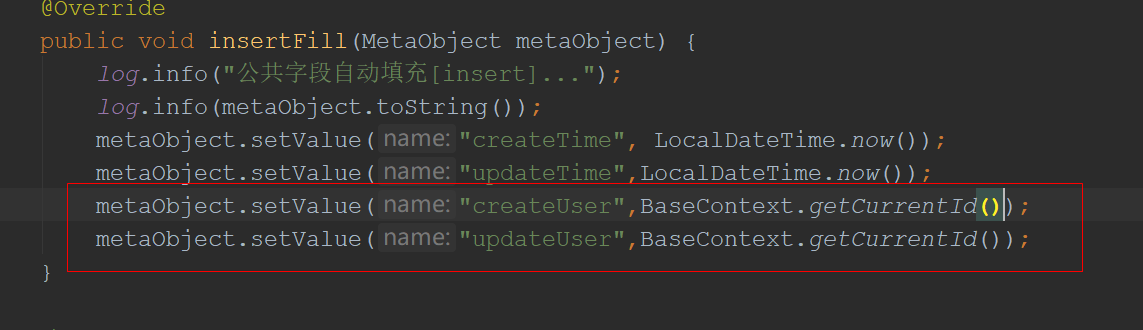
使用ThreadLocal实现当前登录信息的存取
有志者,事竟成 文章持续更新,可以关注【小奇JAVA面试】第一时间阅读,回复【资料】获取福利,回复【项目】获取项目源码,回复【简历模板】获取简历模板,回复【学习路线图】获取学习路线图。 文章目录一、使用…...

高通平台开发系列讲解(Android篇)AudioTrack音频流数据传输
文章目录 一、音频流数据传输通道创建1.1、流程描述1.2、流程图解二、音频数据传输2.1、流程描述2.2、流程图解沉淀、分享、成长,让自己和他人都能有所收获!😄 📢本篇章主要图解AudioTrack音频流数据传输 。 一、音频流数据传输通道创建 1.1、流程描述 AudioTrack在set函…...

BUUCTF-firmware1
题目下载:下载 新题型,记录一下 题目给出了flag形式,md5{网址:端口},下载发现是一个.bin文件 二进制文件,其用途依系统或应用而定。一种文件格式binary的缩写。一个后缀名为".bin"的文件&#x…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...
