C++ 浅谈之 AVL 树和红黑树
C++ 浅谈之 AVL 树和红黑树
HELLO,各位博友好,我是阿呆 🙈🙈🙈
这里是 C++ 浅谈系列,收录在专栏 C++ 语言中 😜😜😜
本系列阿呆将记录一些 C++ 语言重要的语法特性 🏃🏃🏃
OK,兄弟们,废话不多直接开冲 🌞🌞🌞
一 🏠 概述
AVL 树
上文提到对于二叉搜索树有单边树的缺陷,那么对于 STL 关联容器 map、set 等底层结构对其进行了平衡处理,采用平衡树实现
AVL 树,当向二叉搜索树插入新结点后,保证每个结点左右子树高度差绝对值不超过 1 ,降低树高度,减少平均搜索长度
概念
AVL 树是空树或具有如下性质的二叉搜索树
① 左右子树都是 AVL 树
② 左右子树高度之差 ( 简称平衡因子 : 右子树高 - 左子树高 ) 绝对值不超过 1
一棵二叉搜索树高度平衡,它就是 AVL 树。如果它有 n 个结点,其高度可保持在 O(log2N),搜索时间复杂度 O(log2N)
AVL 树节点定义
template<class K,class V>
struct AVLTreeNode
{AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;//定义成三叉链的形式int _bf;//balance factor平衡因子pair<K, V> _kv;//用pair同时存K和V两个数据AVLTreeNode(const pair<K,V>& kv)//节点构造函数:_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0)//平衡因子初始给0,_kv(kv){}
};
AVL 树插入
AVL 树是在二叉搜索树基础上引入平衡因子,插入过程如下
① 按照二叉搜索树方式找到空位置,插入新节点
② 插入新节点后,需要调整节点的平衡因子
③ 插入元素后可能导致 AVL 树左右子树高度不符合条件,需要旋转
AVL 树旋转
AVL树的旋转分为多种,具体举出一种如下图所示(右单旋)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-1k1kVipt-1676620255584)(E:\2022年MD文档\2023 年 MD文档\二月\浅谈系列\C++ 浅谈之 AVL 树和红黑树.assets\企业微信截图_16766174867883.png)]](https://img-blog.csdnimg.cn/15fe146d4b574e33bf7cc2890e01ac8c.png)
Parent 平衡因子为 2 或 -2 ,分以下情况
① 平衡因子为 2,说明右子树高,需要往左边压高度,设 Parent 右子树根为 SubR
当 SubR 平衡因子为 1 时,执行左单旋
当 SubR 平衡因子为 -1 时,执行右左双旋
② 平衡因子为 -2,说明左子树高,需要往右边压高度,设 Parent 左子树根为 SubL
当 SubL 平衡因子为 -1 时,执行右单旋
当 SubL 平衡因子为 1 时,执行左右双旋
旋转完成后,原 Parent 为根子树个高度降低,已经平衡(无需往上更新,直接退出循环)
AVL 树模拟实现
#pragma once
#include<iostream>
#include<assert.h>
#include<string>
using namespace std;template<class K,class V>
struct AVLTreeNode
{AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;//定义成三叉链的形式int _bf;//balance factor平衡因子pair<K, V> _kv;//用pair同时存K和V两个数据AVLTreeNode(const pair<K,V>& kv)//节点构造函数:_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0)//平衡因子初始给0,_kv(kv){}
};template<class K,class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:AVLTree():_root(nullptr){}//拷贝构造和赋值拷贝也需要自己实现AVLTree(const AVLTree<K,V>& kv){_root = Copy(kv._root);}AVLTree<K, V>& operator=(AVLTree<K,V> kv){swap(_root, kv._root);return *this;}~AVLTree(){Destroy(_root);_root = nullptr;}Node* Copy(Node* root){if (root == nullptr)return nullptr;Node* newroot = new Node(root->_key);//建立新节点newroot->_left = Copy(root->_left);//新节点的左右节点再去转换成子问题newroot->_right = Copy(root->_right);return newroot;//最后返回新节点}void Destroy(Node* root){//利用后序遍历去释放节点if (root == nullptr){return;}Destroy(root->_left);Destroy(root->_right);delete root;}V& operator[](const K& key)//重载operator[]{//operator[]的原则是://如果插入成功返回插入都value的引用//如果插入失败则返回V类型默认缺省值pair<Node*, bool> ret = Insert(make_pair(key, V()));//V采用传匿名对象的方式return ret.first->_kv.second;}Node* Find(const pair<K, V>& kv)//查找函数{Node* cur = _root;while (cur){if (kv.first > cur->_kv.first){cur = cur->_right;}else if (kv.first < cur->_kv.first){cur = cur->_left;}else{return cur;}}return nullptr;}void RotateR(Node* parent)//右单旋{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR != nullptr)//注意:这里一定要判断不为空的,因为下面可能会出现空指针的解引用{subLR->_parent = parent;}subL->_right = parent;Node* parentParent = parent->_parent;//一定要在改变链接关系之前把这个指针存下来parent->_parent = subL;//if (parentParent == nullptr)或者采用这个条件也是可以的if(parent==_root){_root = subL;_root->_parent = nullptr;}else{//这里注意:parent还有父母时,链接之前需要注意判断到底是右孩子还是左孩子if (parentParent->_left == parent)parentParent->_left = subL;elseparentParent->_right = subL;subL->_parent = parentParent;//最后还要把父指针关系链接上}parent->_bf = subL->_bf = 0;//最后右单旋完成后平衡因子都要修改成0}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;//先把subR的左孩子赋值给parent的右节点parent->_right = subRL;if (subRL != nullptr)//注意一定要判断是否为空的情况{subRL->_parent = parent;//然后链接parent指针}//然后subR的左节点链接上parentsubR->_left = parent;Node* parentParent = parent->_parent;//提前记录parent->_parent = subR;//if (parentParent == nullptr)if (parent == _root){_root = subR;_root->_parent = nullptr;}else{if (parentParent->_left == parent)parentParent->_left = subR;elseparentParent->_right = subR;subR->_parent = parentParent;}parent->_bf = subR->_bf = 0;}void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;//注意:需要提前存subRL的平衡因子,因为旋转可能引起改变//subRL的平衡因子是双旋的关键节点RotateR(parent->_right);//先进行右旋,并注意旋转点为父节点的右节点RotateL(parent);//再进行左旋,此时旋转点为父节点if (bf == 0){parent->_bf = 0;subR->_bf = 0;subRL->_bf = 0;}else if (bf == 1){parent->_bf = -1;subR->_bf = 0;subRL->_bf = 0;}else if (bf == -1){parent->_bf = 0;subR->_bf = 1;subRL->_bf = 0;}//注意这里处理完成过后sunRL的平衡因子一定都是等于0的else{assert(false);}}void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);//先进行左旋,并注意旋转点为父节点的左节点RotateR(parent);//再进行右旋,此时旋转点为父节点if (bf == 0){parent->_bf = 0;subL->_bf = 0;subLR->_bf = 0;}else if (bf == 1){parent->_bf = 0;subL->_bf = -1;subLR->_bf = 0;}else if (bf == -1){parent->_bf = 1;subL->_bf = 0;subLR->_bf = 0;}//注意这里处理完成过后sunRL的平衡因子一定都是等于0的else{assert(false);}}pair<Node*,bool> Insert(const pair<K, V>& kv){if (_root == nullptr)//根节点为空时先new一个新节点{_root = new Node(kv);return make_pair(_root, true);}Node* cur = _root;Node* parent = nullptr;//先利用while循环去找cur的空位while (cur){if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else{return make_pair(cur, false);}}//将cur插入到相应位置cur = new Node(kv);Node* newnode = cur;//用一个newnode记录一下新节点用以返回if (kv.first > parent->_kv.first){parent->_right = cur;//注意三叉链的链接逻辑顺序,等号左右方向不能反,先把cur链接到父节点的右边cur->_parent = parent;//然后再去把父指针知道父节点}else{parent->_left = cur;cur->_parent = parent;}//进行旋转调整//while(cur!=_root)while (parent){//1.进入循环先对平衡因子进行调整if (cur == parent->_right){parent->_bf++;}else{parent->_bf--;}//分三种情况向上走if (parent->_bf == 0)//平衡因子等于0不需要调整{//为什么不需调整//因为等于0的话,说明底层子树高度不平衡,添加进入新元素后平衡了,只要平衡了高度并没发生变化,不会影响上面的父节点break;}else if (parent->_bf == -1 || parent->_bf == 1){//平衡因子等于-1,说明插入新节点后子树的高度不平衡了,需要继续往上迭代查看父节点是否还满足平衡节点cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){if (parent->_bf == -2)//父节点等于-2,说明左边高,触发右旋的情况{if (cur->_bf == -1)//cur节点等于-1,说明在cur的左边更高,触发右单旋的情况{RotateR(parent);}else//cur等于-1,说明在cur的右边更高,触发左右双旋{RotateLR(parent);}}else//父节点等于1,说明右边更高,触发左旋的情况{if (cur->_bf == 1)//cur节点等于1时,说明在cur的右边更高,触发右单旋的情况{RotateL(parent);}else//cur等于-1,说明在cur的左边更高,触发右左双旋{RotateRL(parent);}}//思考:为什么上面在传参数的时候,都是传parent的节点呢?这样的好处是什么呢break;//调整完成后break退出循环//这里为什么调整完成过后就可以退出,通过旋转调整平衡因子后,parent节点的平衡因子都为0了,调整过后不需要再向上继续查找了}else{assert(false);}}return make_pair(newnode,true);}void _Inorder(Node* root)//中序遍历打印每个节点{if (root == nullptr)return;_Inorder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_Inorder(root->_right);}void Inorder(){_Inorder(_root);cout << endl;}//验证是否为平衡二叉树//1.左子树高度与右子树高度差必须小于1int _Height(Node* root)//求树的高度函数{if (root == nullptr){return 0;}int leftHeight = _Height(root->_left);//递归去子问题求解int rightHeight = _Height(root->_right);return rightHeight > leftHeight ? rightHeight + 1 : leftHeight + 1;}bool _IsBalance(Node* root){if (root == nullptr){return true;}int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);// 2.检查一下每颗树的平衡因子是否正确if (rightHeight - leftHeight != root->_bf){cout << "平衡因子异常:" << root->_kv.first << endl;return false;}return abs(rightHeight - leftHeight) < 2&& _IsBalance(root->_left)&& _IsBalance(root->_right);//分别递归到各自的左右子树再去检查}bool IsAVLTree(){return _IsBalance(_root);}
private:Node* _root;
};
二 🏠 核心
红黑树
红黑树的概念
一种二叉搜索树,在每个结点上增加一个存储位表示结点颜色,Red 或 Black。确保没有一条路径会比其他路径长 2 倍,因而接近平衡
红黑树性质
红黑树的定义
- 每个结点不是红就是黑
- 根节点是黑色
- 一个节点是红,则两个孩子是黑 ( 没有连续红节点 )
- 每条路径上包含相同数量黑节点
- 每个叶子结点都是黑 ( 此处指的是空结点,即 NIL 节点 )
为什么红黑树能保证最长路径中节点个数不会超过最短路径的两倍 ?
假设黑节点数量 N 个,最短路径为 :logN,最长路径为 :2 * logN . 所以最长路径节点数不会超过最短路径的两倍
红黑树节点定义
enum Colour
{RED,BLACK
};//节点的颜色
template<class K, class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;//节点左孩子RBTreeNode<K, V>* _right;//节点右孩子RBTreeNode<K, V>* _parent;//节点的父亲pair<K, V> _kv;//节点中存放的键值对Colour _col;//节点的颜色RBTreeNode(const pair<K,V> kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_col(RED){}
};
为什么节点默认颜色是红色 ?
因为默认颜色黑色,将破坏定义四,其它每条路径都会因该路径增加一个黑节点而不满足红黑树性质,这是一种全局的破坏;默认颜色红色,会破坏定义三,但只会影响当前路径,并不会对其它路径造成影响
红黑树插入操作
可分为两步
按照二叉搜索树规则插入新节点
检测新节点插入后,红黑树性质是否造到破坏
如果父节点是黑色(未违反红黑树任何性质),则不需要调整;
父节点为红色时,违反了定义三不能有连在一起的红色节点
此时对红黑树有多种情况,如下图为其中一种讨论
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Aai00yvJ-1676620255586)(E:\2022年MD文档\2023 年 MD文档\二月\浅谈系列\C++ 浅谈之 AVL 树和红黑树.assets\1676619846457.png)]](https://img-blog.csdnimg.cn/7d53855932dc47098529d0e565b334bd.png)
红黑树模拟实现
#pragma once
#include<iostream>
using namespace std;enum Colour
{RED,BLACK
};//节点的颜色
template<class K,class V>
struct RBTreeNode
{RBTreeNode<K,V>* _left;//节点左孩子RBTreeNode<K,V>* _right;//节点右孩子RBTreeNode<K,V>* _parent;//节点的父亲pair<K,V> _kv;//节点中存放的T类型的数据Colour _col;//节点的颜色RBTreeNode(const pair<K,V> kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_col(RED){}
};template<class K,class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public:RBTree():_root(nullptr){}//拷贝构造和赋值拷贝也需要自行实现这里不做赘述~RBTree(){Destory(_root);_root = nullptr;}void Destory(Node* root){if (root == nullptr){return;}//利用后序遍历释放节点Destory(root->_left);Destory(root->_right);delete root;}void RotateR(Node* parent)//右单旋{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR != nullptr)//注意:这里一定要判断不为空的,因为下面可能会出现空指针的解引用{subLR->_parent = parent;}subL->_right = parent;Node* parentParent = parent->_parent;//一定要在改变链接关系之前把这个指针存下来parent->_parent = subL;//if (parentParent == nullptr)或者采用这个条件也是可以的if (parent == _root){_root = subL;_root->_parent = nullptr;}else{//这里注意:parent还有父母时,链接之前需要注意判断到底是右孩子还是左孩子if (parentParent->_left == parent)parentParent->_left = subL;elseparentParent->_right = subL;subL->_parent = parentParent;//最后还要把父指针关系链接上}}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;//先把subR的左孩子赋值给parent的右节点parent->_right = subRL;if (subRL != nullptr)//注意一定要判断是否为空的情况{subRL->_parent = parent;//然后链接parent指针}//然后subR的左节点链接上parentsubR->_left = parent;Node* parentParent = parent->_parent;//提前记录parent->_parent = subR;//if (parentParent == nullptr)if (parent == _root){_root = subR;_root->_parent = nullptr;}else{if (parentParent->_left == parent)parentParent->_left = subR;elseparentParent->_right = subR;subR->_parent = parentParent;}}pair<Node*, bool> Insert(const pair<K, V> kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;//根节点给黑色return make_pair(_root, true);}Node* cur = _root;Node* parent = nullptr;while (cur)//循环去找空位{if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else if(kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else{return make_pair(cur, false);}}Node* newnode = new Node(kv);newnode->_col = RED;//链接上新节点if (kv.first > parent->_kv.first){parent->_right = newnode;newnode->_parent = parent;}else{parent->_left = newnode;newnode->_parent = parent;}cur = newnode;//父节点存在且父节点为红色时需要继续处理while (parent && parent->_col == RED){Node* grandfather = parent->_parent;//关键看叔叔的脸色if (parent == grandfather->_left){Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED){//具体变色的情况需要画图分析:grandfather->_col = RED;parent->_col = uncle->_col = BLACK;//注意需要继续向上处理,容易忘记cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_left){RotateR(grandfather);//右单旋parent->_col = BLACK;grandfather->_col = RED;}else{RotateL(parent);//先以父节点为旋转点左旋RotateR(grandfather);//再以g为旋转点右旋cur->_col = BLACK;grandfather->_col = RED;}break;//旋转+变色过后一定是满足所有性质的直接退出循环}}else{Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED){uncle->_col = parent->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else // 情况2:+ 情况3:{if (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else // cur == parent->_left{RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return make_pair(newnode, true);}void _InOrder(Node* root)//中序遍历递归打印{if (root == nullptr){return;}_InOrder(root->_left);cout << root->_kv.first << ":"<<root->_kv.second<<endl;_InOrder(root->_right);}void InOrder(){_InOrder(_root);cout << endl;}bool _CheckBlance(Node* root, int blackNum, int count)//balckNum相当于一个标尺,count就是用来记录每条路径的黑节点数目{if (root == nullptr)//如果root走到空节点{if (count != blackNum)//count不等于最左路径的黑色节点数{cout << "黑色节点的数量不相等" << endl;return false;//返回假}return true;//否则返回真}if (root->_col == RED && root->_parent->_col == RED){cout << "存在连续的红色节点" << endl;return false;}if (root->_col == BLACK){count++;}return _CheckBlance(root->_left, blackNum, count)&& _CheckBlance(root->_right, blackNum, count);//再递归到各子树的子问题}bool CheckBlance(){if (_root == nullptr){return true;}if (_root->_col == RED){cout << "根节点是红色的" << endl;return false;}// 找最左路径做黑色节点数量参考值int blackNum = 0;Node* left = _root;while (left){if (left->_col == BLACK){blackNum++;}left = left->_left;}int count = 0;return _CheckBlance(_root, blackNum, count);}
private:Node* _root;
};
红黑树与 AVL 树比较
都是高效平衡二叉树,增删改查时间复杂度都是 O( log2N) ,红黑树不追求绝对平衡,其只需保证最长路径不超过最短路径 2 倍,降低了插入和旋转次数,所以在经常进行增删结构中性能比 AVL 树更优,而且红黑树实现比较简单,所以实际运用中红黑树更多
三 🏠 结语
身处于这个浮躁的社会,却有耐心看到这里,你一定是个很厉害的人吧 👍👍👍
各位博友觉得文章有帮助的话,别忘了点赞 + 关注哦,你们的鼓励就是我最大的动力
博主还会不断更新更优质的内容,加油吧!技术人! 💪💪💪
相关文章:

C++ 浅谈之 AVL 树和红黑树
C 浅谈之 AVL 树和红黑树 HELLO,各位博友好,我是阿呆 🙈🙈🙈 这里是 C 浅谈系列,收录在专栏 C 语言中 😜😜😜 本系列阿呆将记录一些 C 语言重要的语法特性 dz…...

【Kotlin】Kotlin函数那么多,你会几个?
目录标准函数letrunwithapplyalsotakeIftakeUnlessrepeat小结作用域函数的区别作用域函数使用场景简化函数尾递归函数(tailrec)扩展函数高阶函数内联函数(inline)inlinenoinlinecrossinline匿名函数标准函数 Kotlin标准库包含几个…...
饲养员喂养动物-课后程序(JAVA基础案例教程-黑马程序员编著-第四章-课后作业)
【案例4-2】饲养员喂养动物 记得 关注,收藏,评论哦,作者将持续更新。。。。 【案例目标】 案例描述 饲养员在给动物喂食时,给不同的动物喂不同的食物,而且在每次喂食时,动物都会发出欢快的叫声。例如&…...
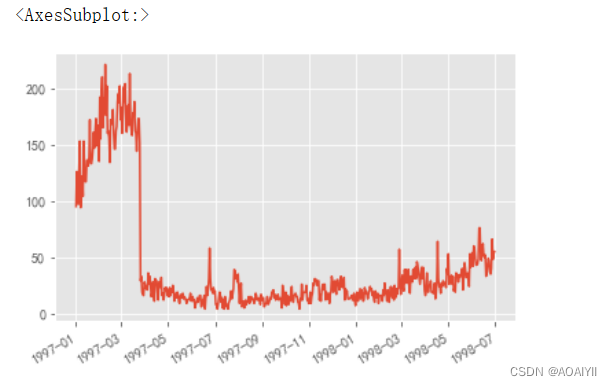
数据分析:消费者数据分析
数据分析:消费者数据分析 作者:AOAIYI 创作不易,如果觉得文章不错或能帮助到你学习,记得点赞收藏评论一下哦 文章目录数据分析:消费者数据分析一、前言二、数据准备三、数据预处理四、个体消费者分析五、用户消费行为总…...

Transformer论文阅读:ViT算法笔记
标题:An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale 会议:ICLR2021 论文地址:https://openreview.net/forum?idYicbFdNTTy 文章目录Abstract1 Introduction2 Related Work3 Method3.1 Vision Transformer3.2…...

Android基础练习解答【2】
文章目录一 填空题二 判断题三 选择题四 简答题一 填空题 1.除了开启开发者选项之外,还需打开手机上的 usb调试 开关,然后才能在手机上调试App。 2.App开发的两大技术路线包括 _原生开发_和混合开发。 3.App工程的编译…...

k8s 搭建
需求:搭建k8s 为后续自动部署做准备进程:安装至少两个ubuntu18.04系统(一个master 一到多个 node)每个系统上都要装上docker 和 kubernetes安装dockersudo su apt-get update#安装相关插件 apt-get install apt-transport-https c…...

安全运维之mysql基线检查
版本加固 选择稳定版本并及时更新、打补丁。 稳定版本:发行6-12个月以内的偶数版本。 检查方法: 使用sql语句:select version(); 检查结果: 存在问题:当前数据库版本较老需要更新 解决方案:前往http://www.mysql…...

跨境电商卖家敦煌、雅虎、乐天、亚马逊测评自养号的重要性!
作为亚马逊、敦煌、乐天、雅虎等跨境的卖家,这两年以来,面对流量越来越贵的现实,卖家需要更加珍惜每次访问listing页面的流量,把转化做好,把流量尽可能转化为更多的订单。 提升转化率的技巧 提升产品转化率࿰…...
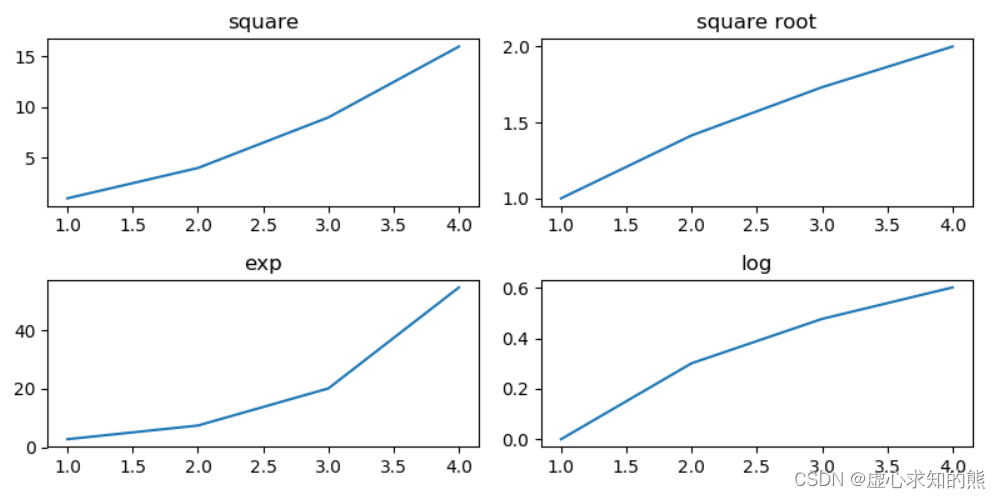
Python 之 Matplotlib xticks 的再次说明、图形样式和子图
文章目录一. 改变 x 轴显示内容 xticks 方法再次说明1. x 轴是数值型数据2. 将 x 轴更改为字符串3. 总结二. 其他元素可视性1. 显示网格:plt.grid()2. plt.gca( ) 对坐标轴的操作三. plt.rcParams 设置画图的分辨率,大小等信息四. 图表的样式参数设置1. …...
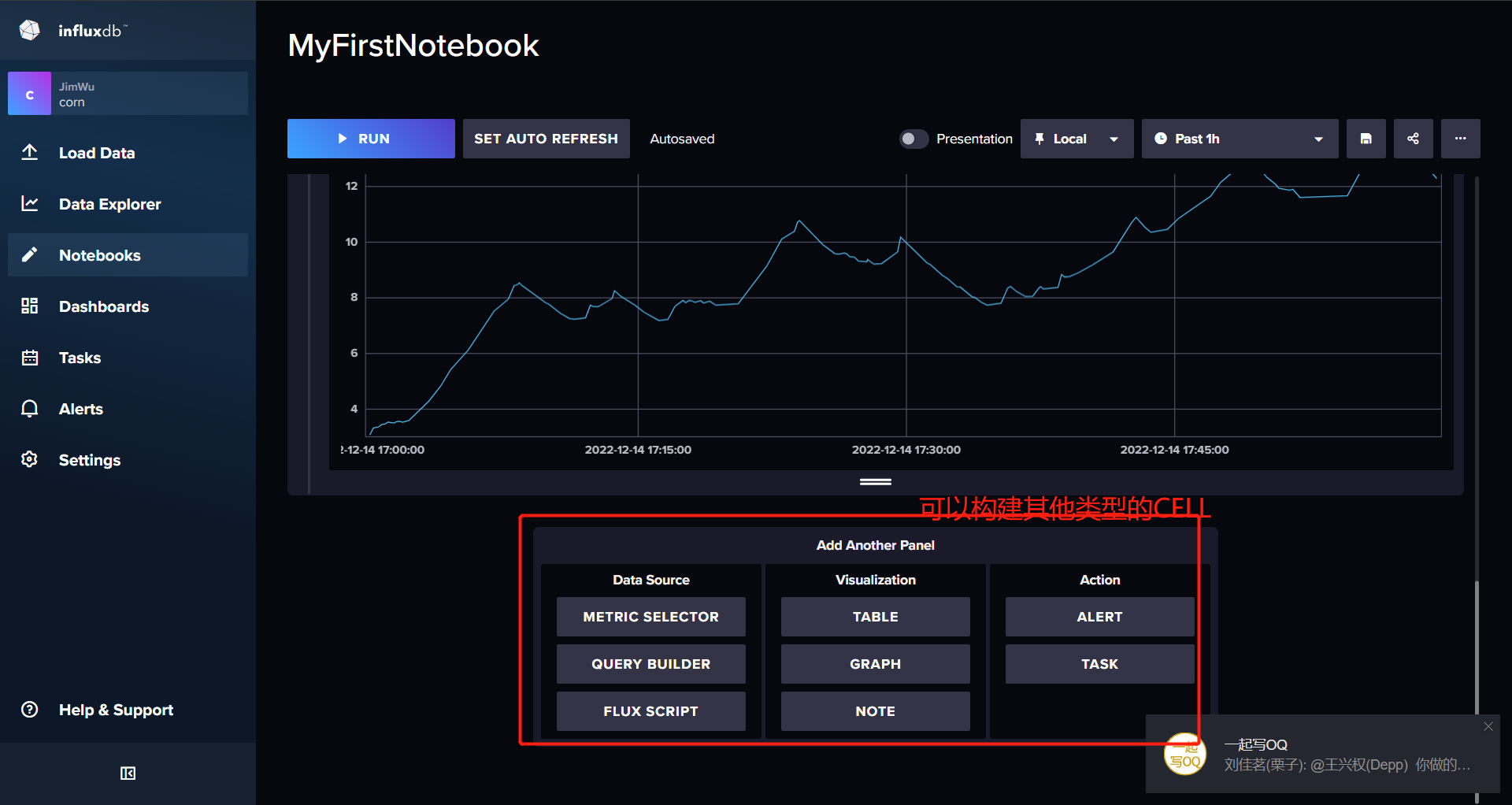
3.InfluxDB WEB使用
结合telegraf做指标数据收集 点击 Load Data -> Telegraf 配置界面 influxDB支持在WEB-UI中生成配置文件 然后利用telegraf通过远程URL请求的方式进行获取 点击CREATE CONFIGURATION 创建telegraf配置文件 选择Bucket InfluxDB提供了很多配置好的监控模板供用户选择 可以…...

git冲突合并
一、版本说明 dev:本地仓库中的dev分支 master:本地仓库中的master分支 remotes/origin/master和origin/master:都是远程仓库上的master分支 二、一个解决冲突的常规流程 1、前提条件:不能在master分支上修改任何文件。master分支…...

项目自动化构建工具make/Makefile
目录 make/Makefile概念和关系 make/Makefie的使用 一个工程中的源文件不计数,其按类型、功能、模块分别放在若干个目录中,makefile定义了一系列的规则来指定,哪些文件需要先编译,哪些文件需要后编译,哪些文件需要重…...

双目客流统计方案的应用原理
双目客流统计客流摄像头采用立体视觉技术实现高度统计功能。基于视差原理。利用双镜头摄取的两幅图像的视差,构建三维场景,在检测到运动目标后。通过计算图像对应点间的位置偏差。获取目标的三维信息,在深度图像中对目标的检测与追踪…...
)
python魔术方法(二)
__getattr__() class A:def __getattr__(self,name):print(f"getting {name}")raise AttributeErroro A() print(o.test)程序调用一个对象的属性,当这个属性不存的时候希望程序做些什么,这里我们打印希望的属性,并且抛出异常 __…...

cmd for命令笔记
语法 help for输出如下: 对一组文件中的每一个文件执行某个特定命令。 FOR %variable IN (set) DO command [command-parameters] %variable 指定一个单一字母可替换的参数。 (set) 指定一个或一组文件。可以使用通配符。 command 指定对每个文件执行的命令。 c…...

4.1 Filter-policy
1. 实验目的 熟悉Filter-policy的应用场景掌握Filter-policy的配置方法2. 实验拓扑 Filter-policy实验拓扑如图4-5所示: 图4-5:Filter-policy 3. 实验步骤 (1) 网络连通性 R1的配置 <Huawei>system-vi…...
day15_常用类
今日内容 上课同步视频:CuteN饕餮的个人空间_哔哩哔哩_bilibili 同步笔记沐沐霸的博客_CSDN博客-Java2301 零、 复习昨日 一、作业 二、代码块[了解] 三、API 四、Object 五、包装类 六、数学和随机 零、 复习昨日 抽象接口修饰符abstractinterface是不是类类接口属性正常属性没…...

【网络原理5】IP协议篇
目录 IP协议报头 4位版本号 4位首部长度 8位服务类型(TOS) 16位总长度 IP拆包 16位标识、3位标志、13位片偏移编辑 8位生存时间(TTL) 8位协议 16位首部校验和 网络地址管理 32位源ip&32位目的ip 方案一:动态分配ip地址 方案2:NAT网络地址转换(使用一个ip代…...

Unity导出WebGL工程,并部署本地web服务器
WebGL打包 设置修改 在Build Settings->PlayerSettings->Other Settings->Rendering 将Color Space 设置为Gamma 将Lightmap Encoding 设置为NormalQuality 在Build Settings->PlayerSettings->Publishing Settings 勾选Decompression Fallback 打包 完成配…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...
