算法的时间复杂度、空间复杂度如何比较?
目录
一、时间复杂度BigO
大O的渐进表示法:
例题一:
例题2:
例题3:冒泡排序的时间复杂度
例题4:二分查找的时间复杂度
书写对数的讲究:
例题5:
实例6:
利用时间复杂度解决编程题
编辑思路一:
思路二:
源码:
思路三:
回顾位操作符
二、空间复杂度详解
概念:
例题1:冒泡排序的空间复杂度是多少?
例题2:单路递归
例题3
解析:
例题4(硬菜,双路递归)
利用空间复杂度解决编程题
思路一:
代码:
思路二:
代码:
思路三:
代码:
一、时间复杂度BigO
首先我们不能以机器运行算法的时间来评判一个算法的时间复杂度,因为即使是相同的算法在不同机器上(机器的个体差异性)运行时间都可能不尽相同,因此我们采用
【大O表示法】——算法的渐进复杂度T(n)=O(f(n))。
就是算执行次数!
首先解读这个公式,f(n)表示代码执行的次数,O表示正比例关系,而T(n)就表示算法的渐进复杂度(就是当一个问题量级增加的时候,算法运行时间增长的一个趋势)。
即找到某条基本语句与问题规模N之间的数学表达式,就是算出了该算法的时间复杂度。
大O的渐进表示法:
实际中我们计算时间复杂度时,我们其实不一定要计算精确的执行次数,而只需要大概执行次数。
大O渐进表示法的规则:
- 用常数1取代运行时间中的所有加法常数。
- 在修改后的运行次数函数中,只保留最高阶项。
- 如果最高阶项存在且不是1,则取出与这个项相乘的常数,使其前面的系数是1,得到的就是大O渐进表达式。
- 用最坏的情况去考虑计算时间复杂度 。
例题一:

我们可以计算出++count语句被执行多少次,从而算出该算法的时间复杂度。
不难计算出这样一个数学函数表达式

例题2:

strchr是一个库函数用来计算某个特定字符在字符串中的位置,实现方法就是循环遍历。
这样时间复杂度一共有三种情况:
1、最幸运,遍历一次就找到
2、最不幸,一直遍历到最后才找到
3、取平均值,遍历到中间才找到
以上三种情况,到底哪种是符合时间复杂度的呢?答案是最坏情况!也就是O(N)
下面是更复杂的一些计算时间复杂度的例题。
一些更复杂的代码,我们不能只看代码去计算时间复杂度,我们要看重代码的思想是什么,底层逻辑!
例题3:冒泡排序的时间复杂度

我们首先要计算最坏的情况,那就是数据本来从小到大顺序排列,而要求从大到小排列,所以全部都需要重新排,第一次n-1,第二次n-2,第三次n-3,以此类推直到最后的1,这就是一个等差数列求和,公差是1,计算得出最高次项是N^2,所以最终O(N)=N^2。
那最好的情况是不是O(1)呢?
答案不是,因为如果已经排好序,我们还需要判断是否有序,判断是否有序就需要时间!所以最好的情况就是O(N)
例题4:二分查找的时间复杂度
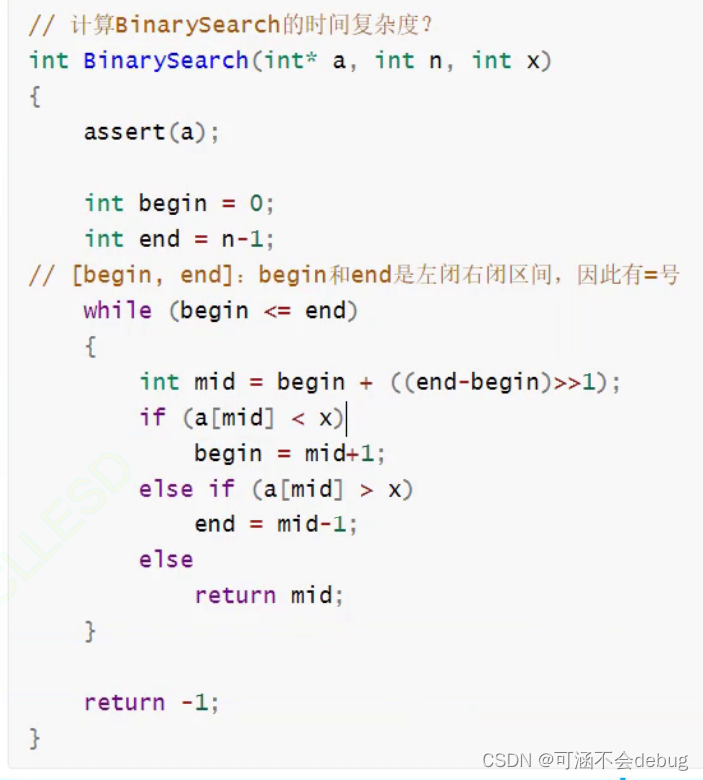
二分查找的最坏情况就是我们要查找的数据在边界,查找区间缩放只剩下一个值时,就是最坏。最坏情况下查找了多少次?除了多少次2,就查找了多少次。
假设区间个数是N,/2/2/2/2一直除到最后区间只剩下一个值。

书写对数的讲究:
由于对数在文本中不好写,支持一些展示公式编辑器才方便,所以时间复杂度简写成logN,只有log以2为底N的对数才可以简写成logN,其他都要写出来。
暴力搜索O(N)和二分查找O(logN)量级的天差地别

例题5:
计算阶乘递归的时间复杂度

注意计算递归的时间复杂度主要看函数被调用的次数,然后再看函数内部的时间复杂度。
递归算法的时间复杂度是多次调用的累加。
我们发现上述代码的递归函数调用了N+1次,而每次函数的内部都是O(1),所以最终的时间复杂度就是O(N).相当于N+1个1的时间复杂度
实例6:

跟上面的代码区别是这是一个双路递归,上面是单路递归

上图是双路递归的调用次数,不难发现规律是以2^n为数量级进行递增,然后再进行等比数列求和,最终计算出来的数量级就是2^n,所以O(N)=2^N

最终的三角形是右下角缺失一块,但并不影响我们的数量级。
但是2^n的时间复杂度算的非常慢,因为CPU能接受是以亿为单位,但是2^n很快就到达CPU的顶峰了。
所以用递归求解斐波那契数列只有理论上可行
利用时间复杂度解决编程题
 思路一:
思路一:
排序+遍历(下一个数不等于下一个数据+1,这个下一个数就是消失的数字)
时间复杂度:O(logN*N)用快排qsort的前提下
思路二:
用0~N等差数列求和公式计算结果减去数组中的值,结果就是消失的数字
时间复杂度:O(N)
源码:
int main()
{int arr[] = { 0,1,3 };int sum = 2 * 3;//求和直接用等差数列的公式计算for (int i=0;i<3;i++){sum -= arr[i];}printf("%d\n", sum);return 0;
}思路三:
单身狗思路:异或,两个成对出现的数字中,出现了一个单独的数字,用异或去解决
int main()
{int arr[] = { 1,3,4 };int ret = 0;for (int i=1;i<=4;i++){ret ^= i;}for (int i=0;i<3;i++){ret ^= arr[i];}printf("%d\n", ret);return 0;
}回顾位操作符
^——异或操作符——对应的二进制相同返回0,对应的二进制位不同,就返回1,注意两个相同的数字异或结果是0,任何一个数据与0异或结果就是它本身,并且异或操作符满足交换律
&——按位与操作符——只要有0,结果就是0
|——按位或操作符——只要有1,结果就是1
二、空间复杂度详解
概念:
空间复杂度也是一个数学表达式,是对一个算法在运行过程中额外临时占用存储空间大小的量度
空间复杂度不是程序占用了多少字节的空间,而是计算的是变量的个数,也采用大O渐进表示法。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显示申请的额外空间来确定。
例题1:冒泡排序的空间复杂度是多少?

首先参数传过来的数组不算入空间复杂度,如果我们是为了让这个数组排序,额外创建了一个数组,这样的数组才算入空间复杂度。
这样计算发现只有end,exchange,i是我们额外创建的变量,所以一共是3个,即空间复杂度是O(1),注意O(1)不代表空间空间复杂度是1个,而是常数个。
例题2:单路递归
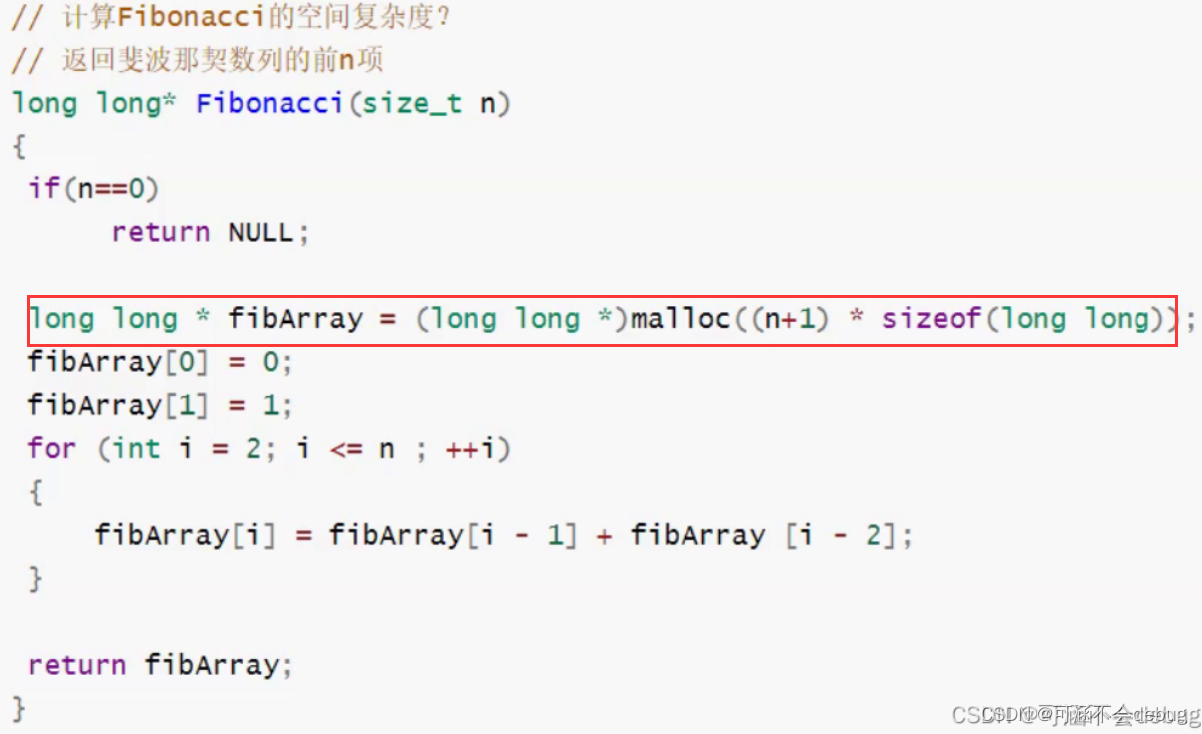
不难看出,为了解决题目,代码额外创建了一个数组,所以最后的空间复杂度就是O(N)
例题3

解析:
假设有N层递归,每次递归需要调用一次函数,而调用函数需要创立栈帧,每调用一次函数,就需要创建一次栈帧,而创建一次栈帧需要常数个的空间,注意栈帧在函数使用完毕后是会销毁的,但是空间复杂度计算的是最大的空间占用,所以只有当递归结束时才计算整体的栈帧。所以最终的空间复杂度就是O(N)。
例题4(硬菜,双路递归)

我们首先要明确这样一个原则,时间是累计的,一去不复返,空间是可以重复利用的。
创建和销毁函数栈帧的潜规则
我们先明白这样一个道理,当一个函数调用完毕后,第一个函数创建的栈帧的空间就会返回操作系统,接着继续再调用另外一个函数,第二个函数创建后需要的栈帧空间就是上一个函数的空间,是一模一样的!下面的例子为证,a和b的地址是一样的。
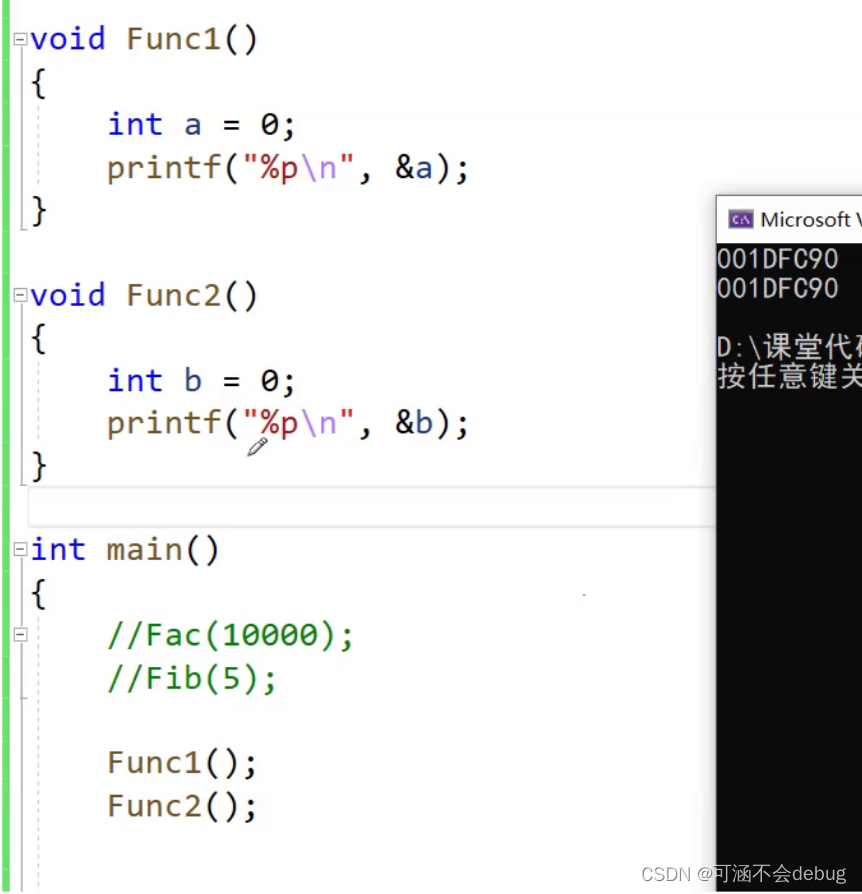
有了上面的基础后,我们还要知道双路递归函数的调用顺序,下图为例。

当我们一路递归调用完毕,函数创建的栈帧销毁,接下来另一个新的函数就会继续用这个空间,重复利用,所以最多额外占用N个空间,即空间复杂度是O(N)。
利用空间复杂度解决编程题

思路一:
先将最后一个数取出来,然后将数组里前面的元素向右移动一位,这样就算是右旋一次,接着进行循环,一共循环k次。
这样的空间复杂度O(1),时间复杂度O(N^2),因为考虑最差情况,不能是KN,因为K是一个变量,情况有好有坏,算复杂度直接取最差的情况。
代码:
int main()
{int arr[] = { 1,2,3,4,5,6,7 };int sz = sizeof(arr) / sizeof(arr[0]);int k = 0;scanf("%d", &k);for (int i=0;i<k;i++){int tmp = arr[sz - 1];for (int j=0;j<sz-1;j++){arr[sz - 1 - j] = arr[sz - 2 - j];}arr[0] = tmp;}for (int i=0;i<sz;i++){printf("%d ", arr[i]);}return 0;
}思路二:
用空间换时间,再开辟一个数组,直接将数据拷贝到新的数组,然后再整体拷贝到原来的数组
时间复杂度就是O(N),因为我们额外开辟了一个数组空间,所以我们的空间复杂度就是O(N)
代码:
int main()
{int arr[] = { 1,2,3,4,5,6,7 };int* tmp = (int*)malloc(sizeof(arr) * sizeof(arr[0]));if (tmp == NULL){perror(malloc);exit(-1);}int k = 0;int sz = sizeof(arr) / sizeof(arr[0]);scanf("%d", &k);//注意memcpy最后一个参数以字节为单位!memcpy(tmp, arr + sz - k % sz, k % sz * sizeof(arr[0]));memcpy(tmp + k % sz, arr, (sz - k % sz) * sizeof(arr[0]));memcpy(arr, tmp, sz * sizeof(arr[0]));for (int i=0;i<sz;i++){printf("%d ", arr[i]);}free(tmp);tmp = NULL;return 0;
}思路三:
三步翻转法:
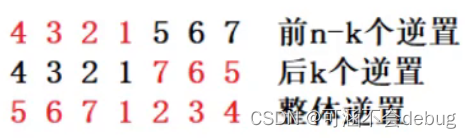
空间复杂度是O(1),时间复杂度是O(N),这就是最优解法!
不容易想到,需要积累!
代码:
void reverse(int* left, int* right)
{while (left <= right){/*int* tmp = left;left = right;right = tmp;*///将两个地址交换int tmp = *left;*left = *right;*right = tmp;left++;right--;}
}int main()
{int arr[] = { 1,2,3,4,5,6,7 };int sz = sizeof(arr) / sizeof(arr[0]);int k = 0;scanf("%d", &k);reverse(arr, arr+sz-k-1);reverse(arr + sz-k, arr + sz - 1);reverse(arr, arr + sz - 1);for (int i=0;i<sz;i++){printf("%d ", arr[i]);}return 0;
}相关文章:

算法的时间复杂度、空间复杂度如何比较?
目录 一、时间复杂度BigO 大O的渐进表示法: 例题一: 例题2: 例题3:冒泡排序的时间复杂度 例题4:二分查找的时间复杂度 书写对数的讲究: 例题5: 实例6: 利用时间复杂度解决编…...

We are the Lights 2023牛客暑期多校训练营4-L
登录—专业IT笔试面试备考平台_牛客网 题目大意:有n*m盏灯,q次操作,每次可以将一整行或一整列的等打开或关闭 1<n,m<1e6;1<q<1e6 思路:对于同一行或者同一列来说,只要最后一次操作时开或者关࿰…...

ant-design-vue中table组件使用customRender渲染v-html
ant-design-vue遇到table中列表数据需要高亮渲染 1、customRender可以使用,但是使用v-html发现不生效还报错 const columns [title: name,dataIndex: name,customRender: (val, row) > {return <span v-html{val}></span>} ]2、customeRender函数…...

若依框架实现后端防止用户重复点击
若依框架实现后端防止用户重复点击 基于自定义注解、切面、Redis实现 1. 添加自定义注解: 代码放置位置:com/ruoyi/common/annotation/RepeatClick.java time: 时间默认0; unit:单位默认 秒; key: 默认空字符串 package com.ruoyi.fra…...

PCA对手写数字数据集的降维
手写数字的数据集结构为(42000, 784),用KNN跑一次半小时,得到准确率在96.6%上下,用随机森林跑一次12秒,准确率在93.8%,虽然KNN效果好,但由于数据量太大,KNN计算太缓慢,所以我们不得不选用随机森林。我们使用了各种技术对手写数据集进行特征选择,最后使用嵌入 法Select…...
Python入门【变量的作用域(全局变量和局部变量)、参数的传递、浅拷贝和深拷贝、参数的几种类型 】(十一)
👏作者简介:大家好,我是爱敲代码的小王,CSDN博客博主,Python小白 📕系列专栏:python入门到实战、Python爬虫开发、Python办公自动化、Python数据分析、Python前后端开发 📧如果文章知识点有错误…...

下级平台级联安防视频汇聚融合EasyCVR平台,层级显示不正确是什么原因?
视频汇聚平台安防监控EasyCVR可拓展性强、视频能力灵活、部署轻快,可支持的主流标准协议有GB28181、RTSP/Onvif、RTMP等,以及厂家私有协议与SDK接入,包括海康Ehome、海大宇等设备的SDK等,能对外分发RTSP、RTMP、FLV、HLS、WebRTC等…...

vue : 无法加载文件 C:\Users\jianfei\AppData\Roaming\npm\vue.ps1,因为在此系统上禁止运行脚本。...
背景 在新电脑上配置vue环境 PS E:\CODE_PROJ\myvue\vue23\P61_使用脚手架\vue_test> npm install -g vue/cli npm WARN deprecated source-map-url0.4.1: See https://github.com/lydell/source-map-url#deprecated npm WARN deprecated urix0.1.0: Please see https://git…...

godot引擎c++源码深度解析系列二
记录每次研究源码的突破,今天已经将打字练习的功能完成了一个基本模型,先来看下运行效果。 godot源码增加打字练习的demo 这个里面需要研究以下c的控件页面的开发和熟悉,毕竟好久没有使用c了,先来看以下代码吧。 //第一排 显示文本…...

专才or 通才
前言 不知道大家有没有这样的感觉,现在的工作专业化程度越来越高,而且是细分方向越来越小。IT领域分到你是计算里面的数据库或者了流式计算引擎,或者是协议存储还是KV存储引擎。 专业化的优势 专业化的程度带来了一个好处就是你在这个领域…...

【小白必看】Python爬虫实战之批量下载女神图片并保存到本地
文章目录 前言运行结果部分图片1. 引入所需库2. 发送请求获取网页内容3. 解析网页内容并提取图片地址和名称4. 下载并保存图片完整代码关键代码讲解 结束语 前言 爬取网络上的图片是一种常见的需求,它可以帮助我们批量下载大量图片并进行后续处理。本文将介绍如何使…...

道本科技||全面建立国有企业合规管理体系
为全面深化国有企业法治建设,不断加强合规管理,防控合规风险,保障企业稳健发展,近日,市国资委印发《常州市市属国有企业合规管理办法(试行)》(以下简称《办法》)…...

CentOS 8上安装和配置Redis
在本篇博客中,我们将演示如何在CentOS 8上安装和配置Redis。我们将首先安装Redis,然后配置Redis以设置密码并允许公开访问。 步骤 1:安装Redis 首先,更新软件包列表: sudo yum update安装Redis: sudo yum …...
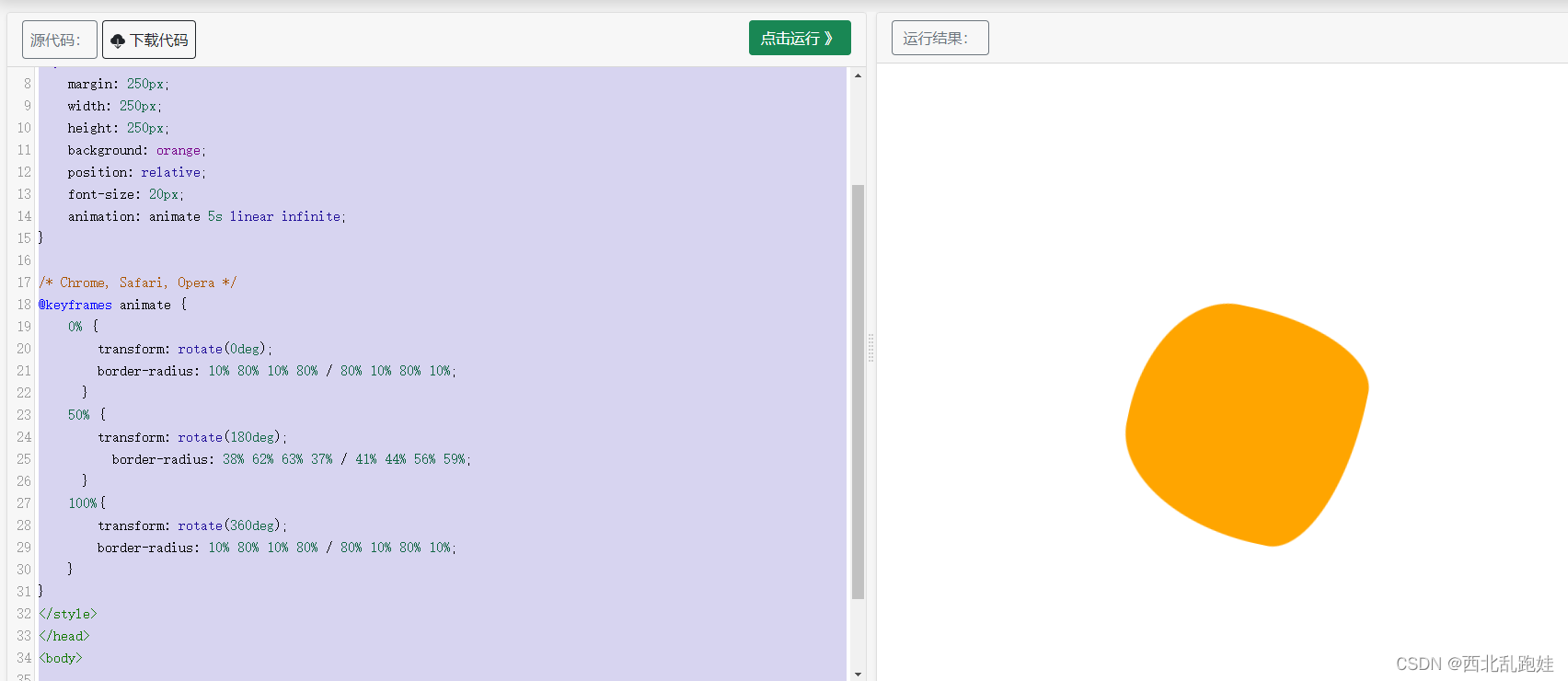
西北乱跑娃 -- CSS动态旋转果冻效果
<!DOCTYPE html> <html> <head> <meta charset"utf-8"> <title>旋转果冻</title> <style> #myDIV {margin: 250px;width: 250px;height: 250px;background: orange;position: relative;font-size: 20px;animation: anima…...

解决安装office出现1402错误和注册表编辑器无法设置安全性错误
写在前面 可能是由于之前的office没有卸载干净,看了很多文章,也有的说是使用了Windows Installer Clean Up卸载office的缘故,最后导致的结果是出现了再次安装office时出现了1402错误,而在解决1402错误的过程中,修改所…...
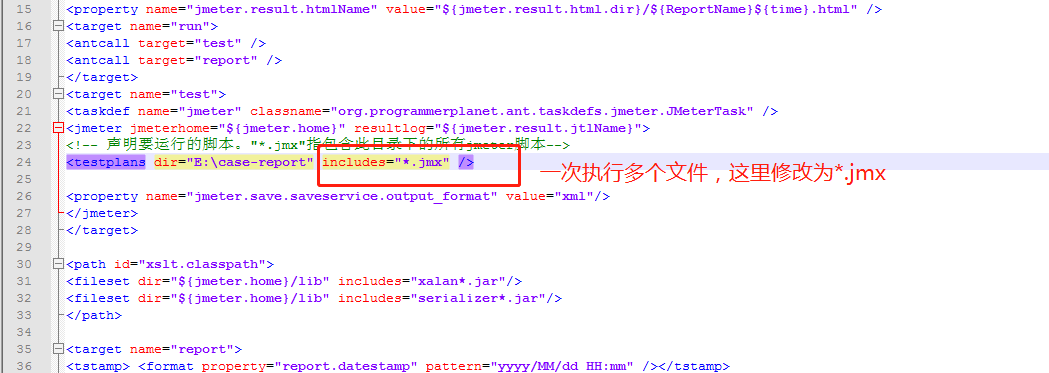
Jmeter接口自动化生成测试报告html格式
jmeter自带执行结果查看的插件,但是需要在jmeter工具中才能查看,如果要向领导提交测试结果,不够方便直观。 笔者刚做了这方面的尝试,总结出来分享给大家。 这里需要用到ant来执行测试用例并生成HTML格式测试报告。 一、ant下载安…...

移动IP的原理
目的 使得移动主机在各网络之间漫游时,仍然能保持其原来的IP地址不变 工作步骤 代理发现与注册 主机A:主机A移动到外地网络后,通过“代理发现协议”,与外地代理建立联系,并从外地代理获得一个转交地址,…...

uView 在 uni-app 中的使用
文章目录 一、uView是什么?1.uView 安装2.uView 在 uni-app 中的使用 一、uView是什么? 提示:正文内容: uView 官网: https://www.uviewui.com uView 是 uni-app 生态专用的 UI 框架 关于uView的取名来由,…...

netcat和netstat使用
Linux是一款受欢迎的开源操作系统,在Linux系统中要安装用于终端连接的nc(netcat)工具,可以帮助我们快速管理网络服务,在此文中,我们将介绍如何在Linux系统下安装nc工具的详细步骤。 一.安装nc工具 1.首先…...
mybatisPlus高级篇
文章目录 主键生成策略介绍AUTO策略INPUT策略ASSIGN_ID策略ASSIGN_UUID策略NONE策略 MybatisPlus分页分页插件自定义分页插件 ActiveRecord模式SimpleQuery工具类SimpleQuery介绍listmapGroup 主键生成策略介绍 主键:在数据库中,主键通常用于快速查找和…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...
