【图论】LCA(倍增)
一.LCA介绍
![]()
LCA通常指的是“最近共同祖先”(Lowest Common Ancestor)。LCA是一种用于解决树或图结构中两个节点的最低共同祖先的问题的算法。
在树结构中,LCA是指两个节点的最近层级的共同祖先节点。例如,考虑一棵树,其中节点A是节点B和节点C的祖先,而节点D是节点B和节点C的共同祖先,但节点D不是最低层级的共同祖先。在这种情况下,LCA就是节点D。
LCA算法在计算机科学中有广泛的应用,例如在计算树的最近公共祖先、解决图的连通性问题、计算有向无环图(DAG)的最近公共祖先等方面。常见的LCA算法包括基于深度优先搜索(DFS)的算法、基于倍增法的算法和Tarjan算法等。
LCA算法的实现方式取决于所使用的数据结构和具体问题的要求。它可以通过预处理树结构,计算和存储每个节点的深度或其他相关信息,以加快查询的速度。LCA算法的时间复杂度通常为O(logN)或O(1),其中N是树或图中的节点数量。
总之,LCA算法是解决树或图结构中两个节点最低共同祖先的问题的一种常见算法。
二.倍增法求LCA
![]()
倍增法(Binary Lifting)是一种常用的求解最低共同祖先(LCA)问题的算法。它通过预处理和存储每个节点的跳跃祖先,以实现快速查询LCA的目的。下面是倍增法求解LCA的详细步骤:
-
预处理:对于每个节点v,计算并存储它的第2^i个祖先,其中i从0开始逐渐增加。这可以通过深度优先搜索(DFS)遍历树来完成。对于根节点,其第2^i个祖先就是根节点本身。对于其他节点v,其第2^i个祖先可以通过它的第2^(i-1)个祖先的第2^(i-1)个祖先来计算。
-
查询LCA:给定两个节点u和v,首先比较它们的深度,假设u的深度大于v的深度。然后,通过不断向上跳跃u的祖先,使得u和v的深度相等。具体步骤如下:
- 如果u和v的深度不相等,将u向上跳跃到与v深度相等的位置。这可以通过从最高位开始逐渐减小的方式进行,即从最大的i开始,如果u的第2^i个祖先的深度大于等于v的深度,则将u跳跃到第2^i个祖先。
- 然后,同时向上跳跃u和v,直到它们的第一个公共祖先出现。这可以通过从最高位开始逐渐减小的方式进行,即从最大的i开始,如果u的第2^i个祖先和v的第2^i个祖先不相等,则将u和v同时跳跃到它们的第2^i个祖先。
- 最后,u和v的第一个公共祖先就是LCA。
倍增法求解LCA的时间复杂度为O(logN),其中N是树中的节点数量。这是因为在查询LCA时,每次跳跃都会将节点的深度减半,直到找到LCA为止。
总结起来,倍增法是一种通过预处理和存储节点的跳跃祖先来求解LCA问题的算法。它具有较低的时间复杂度,并且适用于静态树结构,即树结构不会发生变化的情况下。
三.题目
P3379 【模板】最近公共祖先(LCA) - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
四.代码
#include<bits/stdc++.h>
#define maxn 500005
using namespace std;
int n,m,s; //点,次数,根节点
//链式前向星
int cnt=0,head[maxn];
struct Edge{int u,v,next;
}edge[maxn<<1];
void add(int u,int v){edge[++cnt]=(Edge){u,v,head[u]};head[u]=cnt;
}
//建树
int depth[maxn],p[maxn][25];
void dfs(int u,int fa){p[u][0]=fa;depth[u]=depth[fa]+1;for(int i=head[u];i;i=edge[i].next){int v=edge[i].v;if(v==fa) continue; //防止套娃,无线循环dfs(v,u); }
}
int lca(int x,int y){if(depth[x]<depth[y]) swap(x,y);for(int j=24;j>=0;j--){if(depth[x]-(1<<j)>=depth[y]){x=p[x][j]; //往上走 }}//特判&&巧合if(x==y) return x;//现在x和y深度差不多,同时上升for(int j=24;j>=0;j--){if(p[x][j]!=p[y][j]){x=p[x][j]; y=p[y][j];}} return p[x][0];
}
int main(){cin>>n>>m>>s;for(int i=1;i<n;i++){int u,v;cin>>u>>v;add(u,v);add(v,u);}dfs(s,0); //建树 //预处理 for(int j=1;(1<<j)<=n;j++){ //长度 2^j<=n for(int i=1;i<=n;i++){p[i][j]=p[p[i][j-1]][j-1];}} //输出答案&&LCAwhile(m--){int x,y;cin>>x>>y;cout<<lca(x,y)<<endl;} return 0;
}五.卡住笔者的一个小问题
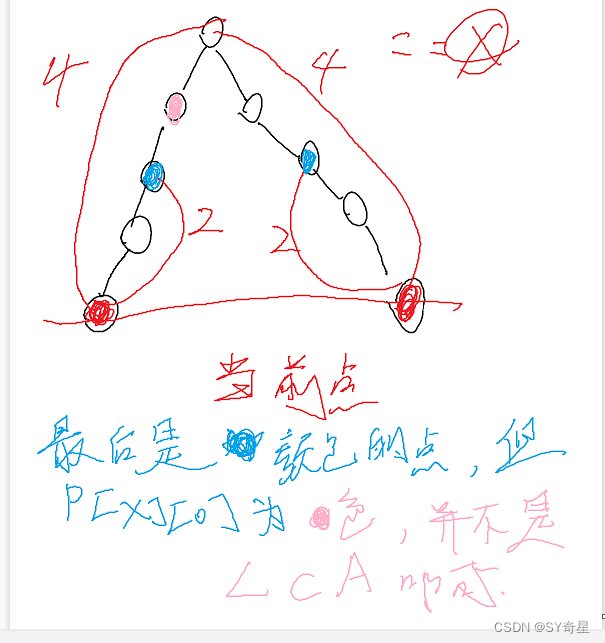
六.answer:
注意: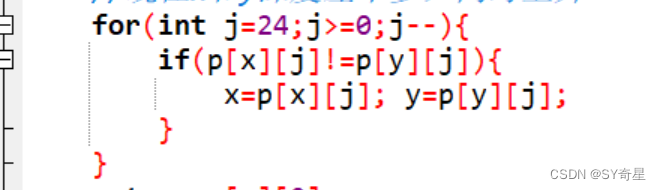
找到p[x][j]!=p[y][j]的时候,并没有直接break;
而是赋值后继续,也就是意味着(结合我的疑问)j再=0,再往上跳1步才结束
这时就成功到达pick点,最后return p[x][0]即为LCA;
其实就妙在遍历中找到!=时,赋值后继续遍历,这就解决了LCA不在倍增数的情况!
相关文章:

【图论】LCA(倍增)
一.LCA介绍 LCA通常指的是“最近共同祖先”(Lowest Common Ancestor)。LCA是一种用于解决树或图结构中两个节点的最低共同祖先的问题的算法。 在树结构中,LCA是指两个节点的最近层级的共同祖先节点。例如,考虑一棵树,…...

QT 使用串口
目录 1.1.1 添加库,添加类 1.1.2 定义串口 1.1.3 搜索串口 1.1.4 设置和打开串口 1.1.5 读取数据 1.1.6 发送数据 1.1.7 关闭串口 1.1.1 添加库,添加类 首先,QT5 是自带 QSerialPort(Qt5 封装的串口类)这个类的,使用时…...
GitHub上怎么寻找项目?
前言 下面由我精心整理的关于github项目资源搜索的一些方法,这些方法可以帮助你更快更精确的搜寻到你需要的符合你要求的项目。 写文章不易,如果这一篇问文章对你有帮助,求点赞求收藏~ 好,下面我们直接进入正题——> 首先我…...

如何快速用Go获取短信验证码
要用Go获取短信验证码,通常需要连接到一个短信服务提供商的API,并通过该API发送请求来获取验证码。由于不同的短信服务提供商可能具有不同的API和授权方式,我将以一个简单的示例介绍如何使用Go语言来获取短信验证码。 在这个示例中࿰…...
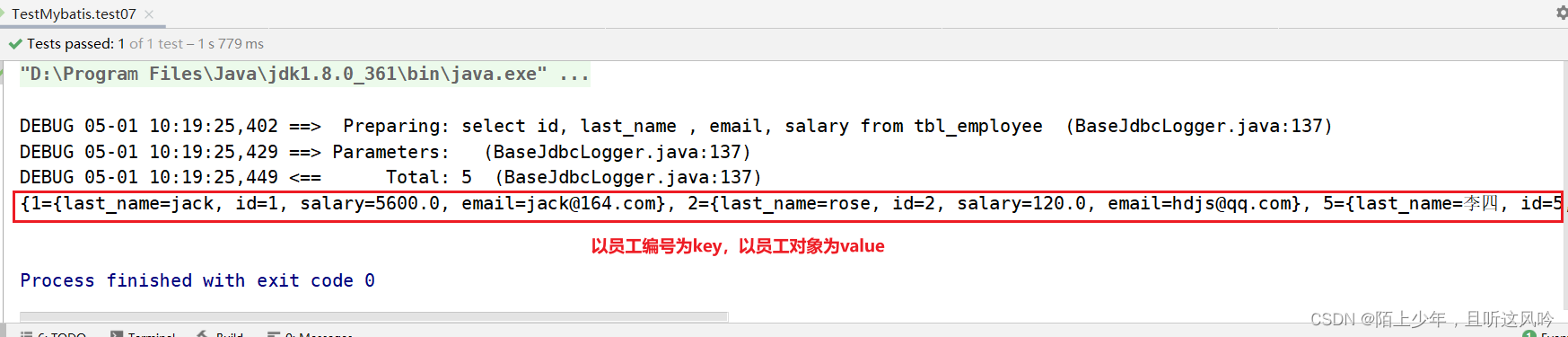
详解Mybatis查询之resultType返回值类型问题【4种情况】
编译软件:IntelliJ IDEA 2019.2.4 x64 操作系统:win10 x64 位 家庭版 Maven版本:apache-maven-3.6.3 Mybatis版本:3.5.6 文章目录 引言一、查询单行数据返回单个对象二、查询多行数据返回对象的集合三、 查询单行数据返回Map[Key,…...
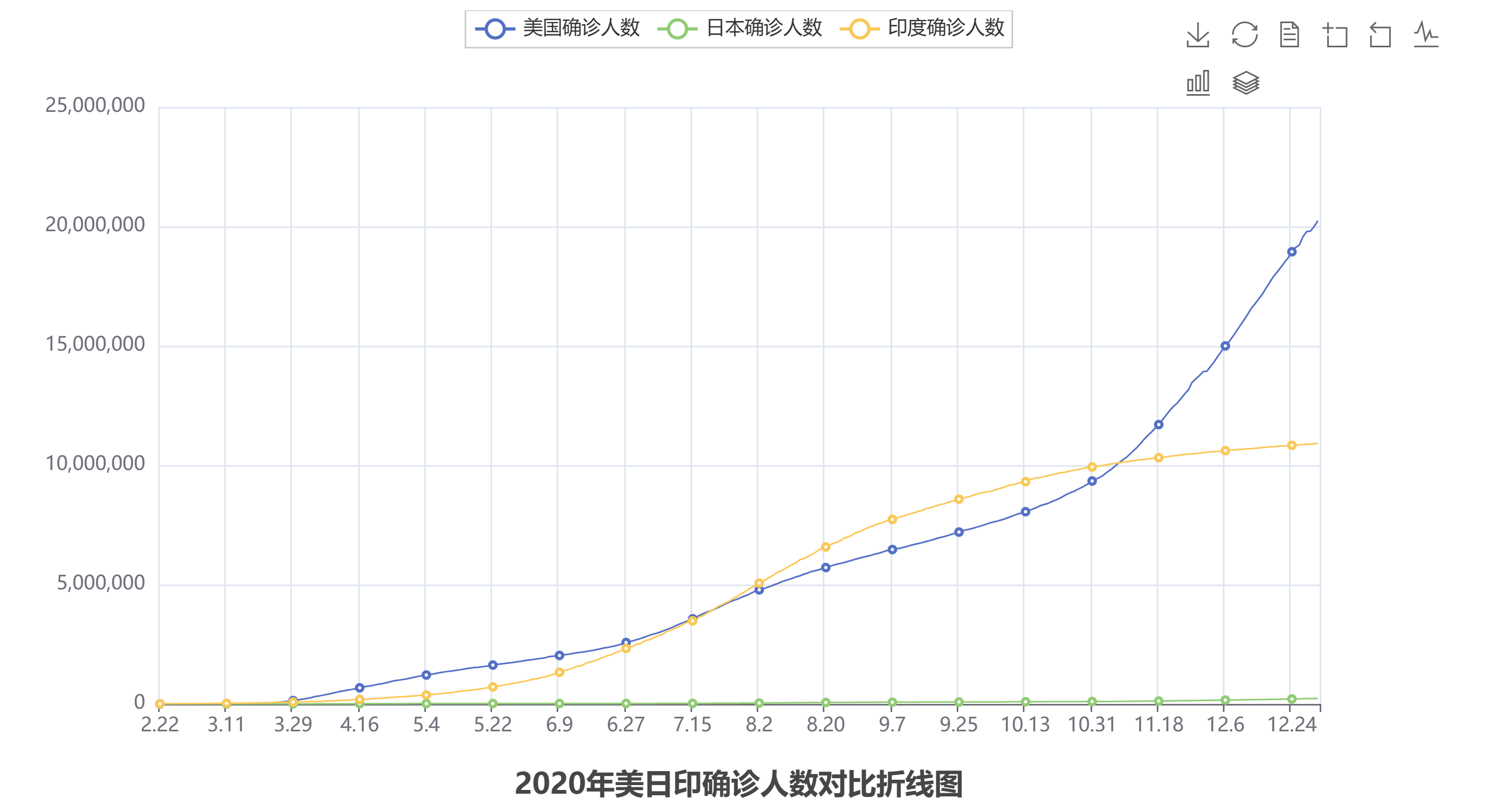
Python-Python基础综合案例:数据可视化 - 折线图可视化
版本说明 当前版本号[20230729]。 版本修改说明20230729初版 目录 文章目录 版本说明目录知识总览图Python基础综合案例:数据可视化 - 折线图可视化json数据格式什么是jsonjson有什么用json格式数据转化Python数据和Json数据的相互转化 pyecharts模块介绍概况如何…...
)
CSS盒子模型(HTML元素布局)
CSS盒子模型是一种用于描述HTML元素布局的模型,它将每个元素看作是一个矩形的盒子,每个盒子由内容、内边距、边框和外边距组成。 盒子模型包括以下几个部分: 内容区域(Content) 内容区域是盒子中实际显示内容的部分&am…...
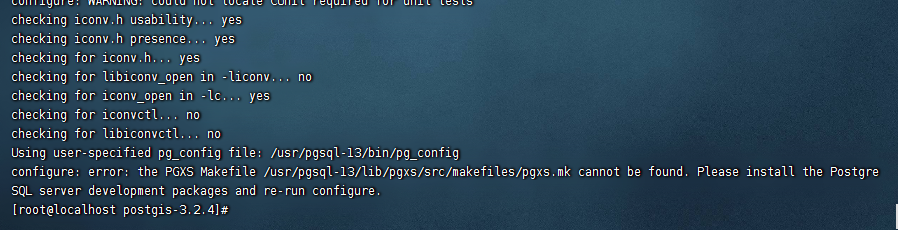
PostgreSQL-Centos7源码安装
卸载服务器上的pg13 本来是想删除原来的postgis重新源码安装就行,但是yum安装的PostgreSQL不能直接使用,会提示以下问题: 之前服务是用yum安装的,现在需要删除 -- 删除数据的postgis插件 drop extension postgis; drop extension postgis cascade;删除相关安装包 # 查询…...
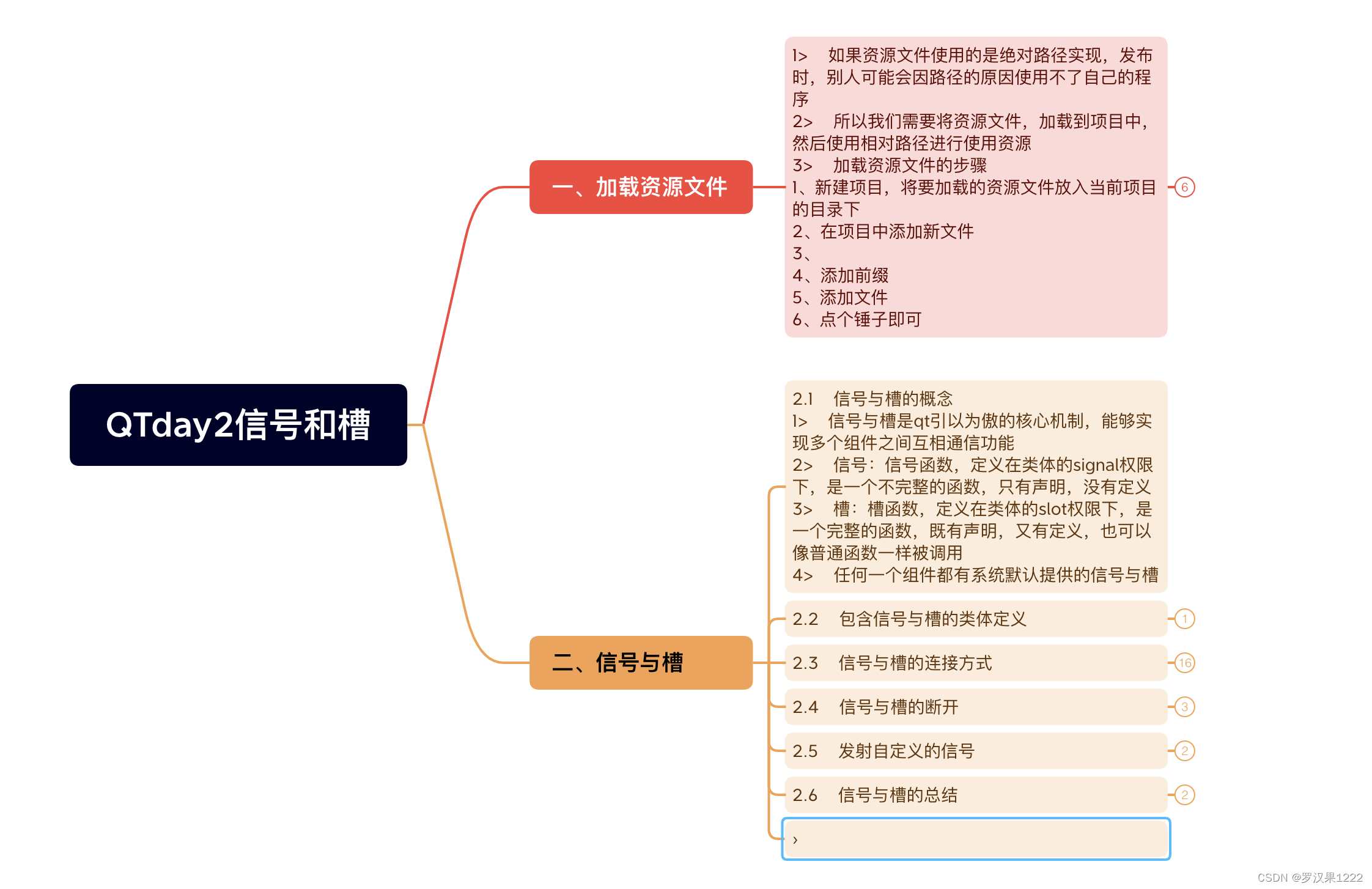
QTday2信号和槽
点击登录按钮,关闭Widget登录窗口,打开QQList窗口 widget.cpp #include "widget.h"void my_setupUI(Widget *w);Widget::Widget(QWidget *parent): QWidget(parent) {my_setupUI(this); }Widget::~Widget() { }void Widget::login_slots() {//fixemit jump_signal(…...
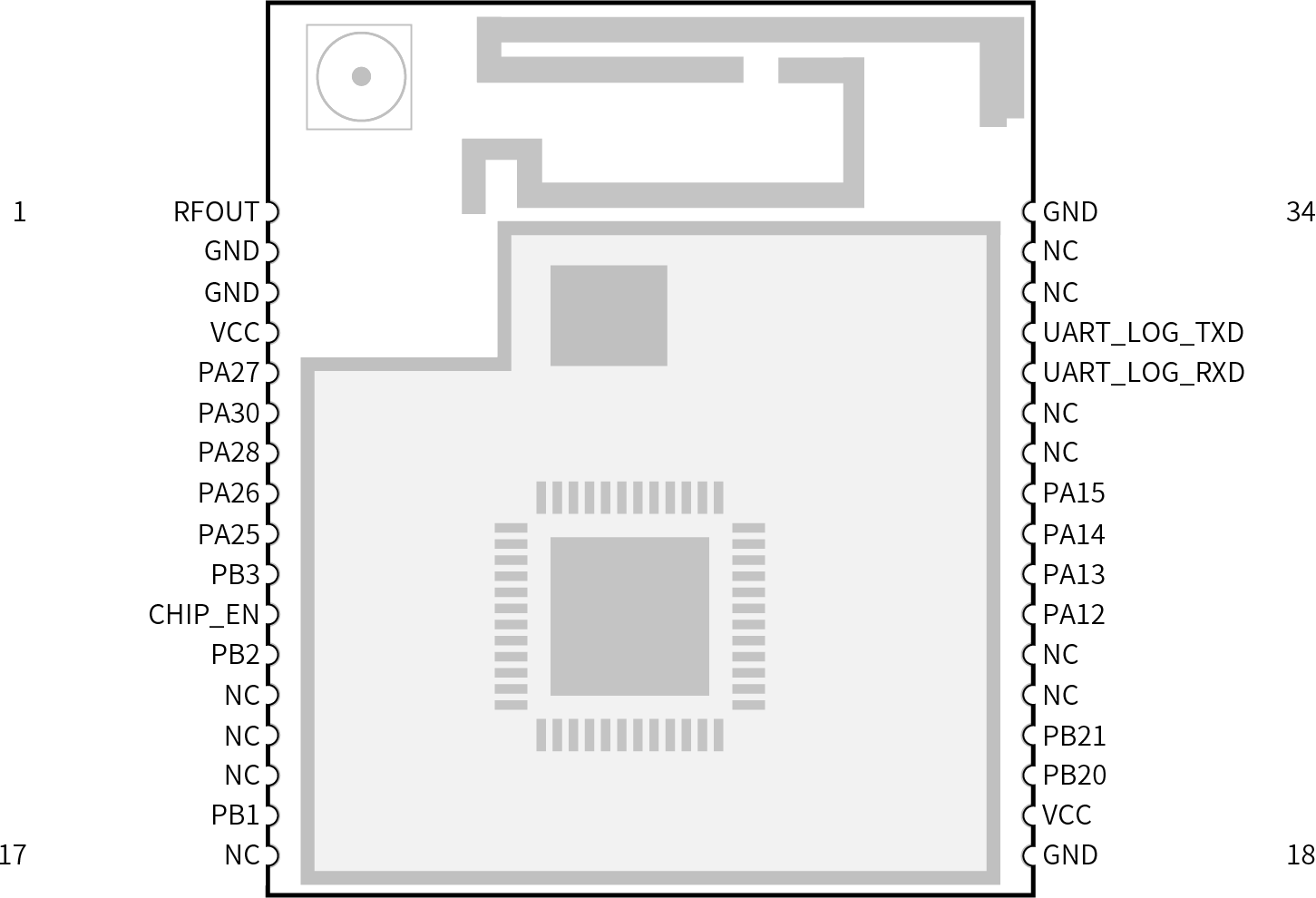
信驰达推出RTL8720DN系列2.4G和5G双频Wi-Fi+蓝牙二合一模块
近日,领先的无线物联网通信模块厂商深圳信驰达科技RF-star推出了基于RTL8720DN SoC的2.4 GHz和5 GHz双频Wi-Fi蓝牙二合一模块—RF-WM-20DNB1。 图 1信驰达RF-WM-20DNB1 Wi-Fi模块 RF-WM-20DNB1是一款低功耗单芯片无线蓝牙和Wi-Fi组合模块,支持双频(2.4 G…...
【LeetCode】剑指 Offer Ⅱ 第1章:整数(5道题) -- Java Version
题库链接:https://leetcode.cn/problem-list/e8X3pBZi/ 题目解决方案剑指 Offer II 001. 整数除法快速除 ⭐剑指 Offer II 002. 二进制加法模拟:StringBuilder ⭐剑指 Offer II 003. 前 n 个数字二进制中 1 的个数动规:res[i] res[i & (…...
解析数据可视化工具:如何选择最合适的软件
在当今信息爆炸的时代,数据已成为各行各业的重要资源。为了更好地理解和分析数据,数据可视化成为一种必不可少的工具。市面上数据可视化工具不说上千也有上百,什么帆软、powerbi、把阿里datav,腾讯云图、山海鲸可视化等等等等&…...

大数据面试题之Elasticsearch:每日三题(七)
大数据面试题之Elasticsearch:每日三题 1.Elasticsearch索引文档的流程?2.Elasticsearch更新和删除文档的流程?3.Elasticsearch搜索的流程? 1.Elasticsearch索引文档的流程? 协调节点默认使用文档ID参与计算(也支持通过routing)&a…...
ubuntu20.04 安装 Qt5.15
目录 安装前工作 选择安装QT的哪个版本 安装时候选择哪些组件 安装Qt5.15 在线安装 我选择的组件 源码包安装 测试 安装前工作 ubuntu20.04.3安装Qt6.22操作步骤_ubuntu安装qt6_sonicss的博客-CSDN博客 # 安装g、gcc编译器 sudo apt-get install build-essential 安装l…...

web之标签元素转换成图片、a标签元素下载图片、获取浏览器窗口名称、重命名、元素定位、旋转、拉伸文字、文字向心对齐
文章目录 准备版本二的效果图版本一htmlJavaScript 版本二htmlJavaScript 准备 NPM下载指令 npm install dom-to-image框架加载 in ES6 import domtoimage from dom-to-image;in ES5 var domtoimage require(dom-to-image);CDN(标签)加载 案例 <script src"dist/dom…...
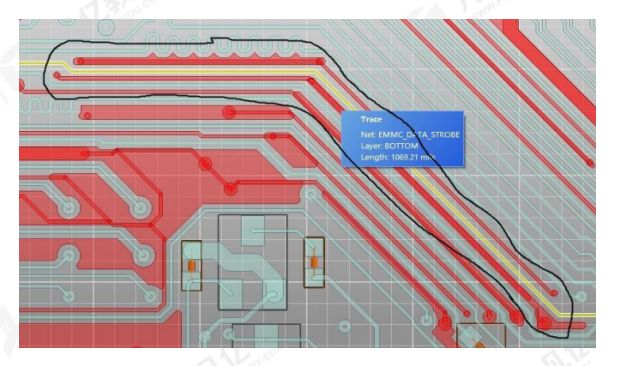
你应该知道的关于PCB布线的31条建议
1、走线长度应包含过孔和封装焊盘的长度。 2、布线角度优选135角出线方式,任意角度出线会导致制版出现工艺问题。 图1 PCB布线的角度 3、布线避免直角或者锐角布线,导致转角位置线宽变化,阻抗变化,造成信号反射,如图2…...
)
matlab中dir的各种使用方法(包括递归遍历子文件夹)
遍历文件夹1下的所有文件夹和文件(不会递归遍历): listdir(’ D:\文件夹1’);遍历文件夹1及其所有子文件夹下的所有文件夹和文件(会递归遍历): listdir(’ D:\文件夹1\** );遍历文件夹1下的所有csv文件&…...

软件测试/测试开发丨Selenium环境安装与使用
Selenium 官方网站: www.selenium.dev/ 简介: 用于web浏览器测试的工具;支持的浏览器包括IE,Firefox,Safari,Chrome,Edge等;使用简单,可使用Java,Python等…...

WPF实战学习笔记15-使用Memo类的GetAll接口
使用Memo类的GetAll接口 总体参照上节即可 创建MemoService接口 新建文件Mytodo/Service/IMemoService.cs using MyToDo.Share.Models; using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks;namespace M…...
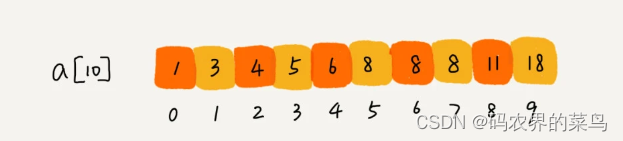
算法与数据结构-二分查找
文章目录 什么是二分查找二分查找的时间复杂度二分查找的代码实现简单实现:不重复有序数组查找目标值变体实现:查找第一个值等于给定值的元素变体实现:查找最后一个值等于给定值的元素变体实现:查找最后一个小于给定值的元素变体实…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...
