算法与数据结构-二分查找
文章目录
- 什么是二分查找
- 二分查找的时间复杂度
- 二分查找的代码实现
- 简单实现:不重复有序数组查找目标值
- 变体实现:查找第一个值等于给定值的元素
- 变体实现:查找最后一个值等于给定值的元素
- 变体实现:查找最后一个小于给定值的元素
- 变体实现:查找第一个大于给定值的元素
- 二分查找的局限性
什么是二分查找
二分查找针对的是一个有序的数据集合,查找思想有点类似分治思想。每次都通过跟区间的中间元素对比,将待查找的区间缩小为之前的一半,直到找到要查找的元素,或者区间被缩小为 0。
我们来举个例子,假设只有 10 个订单,订单金额分别是:8,11,19,23,27,33,45,55,67,98。现在要查找金额为19的订单是否存在,利用二分思想,每次都与区间的中间数据比对大小,缩小查找区间的范围。为了更加直观,我画了一张查找过程的图。其中,low 和 high 表示待查找区间的下标,mid 表示待查找区间的中间元素下标。
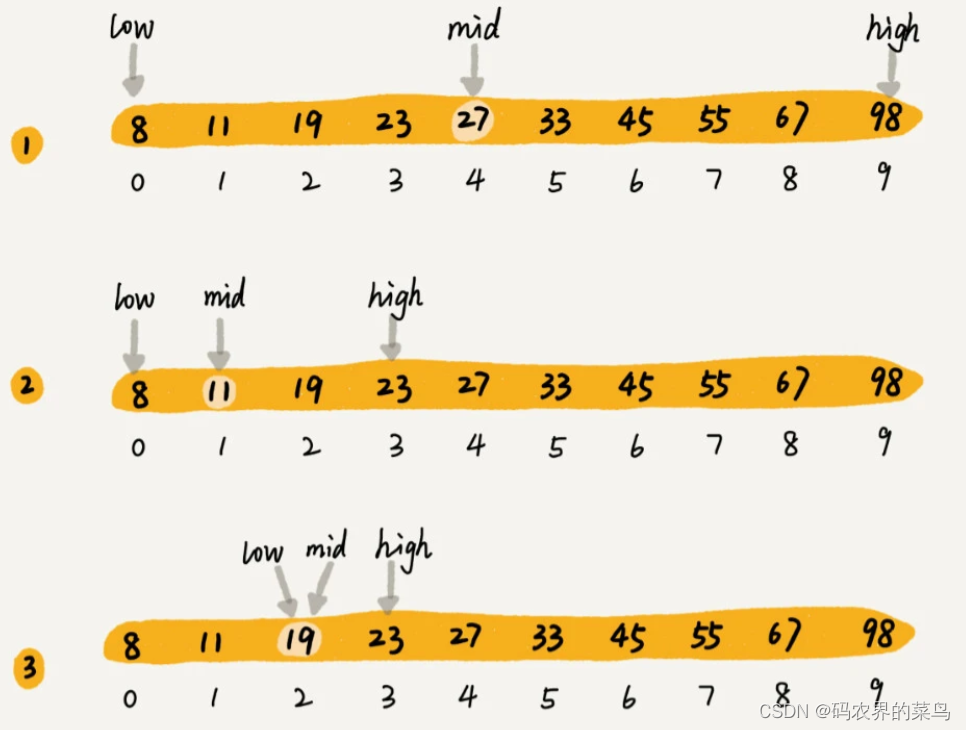
二分查找的时间复杂度
我们假设数据大小是 n,每次查找后数据都会缩小为原来的一半,也就是会除以 2。最坏情况下,直到查找区间被缩小为空,才停止。

可以看出来,这是一个等比数列。其中 n/2k=1 时,k 的值就是总共缩小的次数。而每一次缩小操作只涉及两个数据的大小比较,所以,经过了 k 次区间缩小操作,时间复杂度就是 O(k)。通过 n/2k=1,我们可以求得 k=log2n,所以时间复杂度就是 O(logn)。
O(logn) 这种对数时间复杂度是一种极其高效的时间复杂度,有的时候甚至比时间复杂度是常量级 O(1) 的算法还要高效。为什么这么说呢?
因为 logn 是一个非常“恐怖”的数量级,即便 n 非常非常大,对应的 logn 也很小。比如 n 等于 2 的 32 次方,这个数很大了吧?大约是 42 亿。也就是说,如果我们在 42 亿个数据中用二分查找一个数据,最多需要比较 32 次。
我们前面讲过,用大 O 标记法表示时间复杂度的时候,会省略掉常数、系数和低阶。对于常量级时间复杂度的算法来说,O(1) 有可能表示的是一个非常大的常量值,比如 O(1000)、O(10000)。所以,常量级时间复杂度的算法有时候可能还没有 O(logn) 的算法执行效率高。
二分查找的代码实现
简单实现:不重复有序数组查找目标值
最简单的情况就是有序数组中不存在重复元素,我们在其中用二分查找值等于给定值的数据。我用 Java 代码实现了一个最简单的二分查找算法。
public static int bSearch(int[] arr, int startIndex, int endIndex, int target) {// 递归推出条件if (startIndex > endIndex) {return -1;}// 取折中索引int mid = (startIndex + endIndex) / 2;// 折中值比较if (arr[mid] == target) {return mid;}if (arr[mid] > target) {return bSearch(arr, startIndex, mid - 1, target);}return bSearch(arr, mid + 1, endIndex, target);}
变体实现:查找第一个值等于给定值的元素
比如下面这样一个有序数组,其中,a[5],a[6],a[7]的值都等于 8,是重复的数据。我们希望查找第一个等于 8 的数据,也就是下标是 5 的元素。
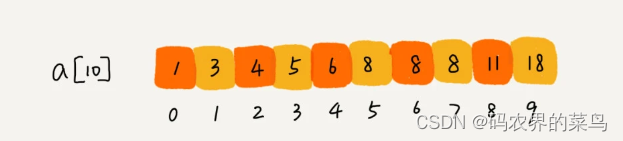
public static int bSearchFirst(int[] arr, int startIndex, int endIndex, int target) {// 递归推出条件if (startIndex > endIndex) {return -1;}// 取折中索引int mid = (startIndex + endIndex) / 2;// 折中值比较if (arr[mid] == target) {if (mid - 1 >= startIndex && arr[mid - 1] == target) {return bSearchFirst(arr, startIndex, mid - 1, target);}return mid;}if (arr[mid] > target) {return bSearchFirst(arr, startIndex, mid - 1, target);}return bSearchFirst(arr, mid + 1, endIndex, target);}
变体实现:查找最后一个值等于给定值的元素
还是上面那个数组,我们的目标如果是查找最后一个等于8的,也就是下表为7的元素。
public static int bSearchLast(int[] arr, int startIndex, int endIndex, int target) {// 递归推出条件if (startIndex > endIndex) {return -1;}// 取折中索引int mid = (startIndex + endIndex) / 2;// 折中值比较if (arr[mid] == target) {if (mid + 1 <= endIndex && arr[mid + 1] == target) {return bSearchLast(arr, mid + 1, endIndex, target);}return mid;}if (arr[mid] > target) {return bSearchLast(arr, startIndex, mid - 1, target);}return bSearchLast(arr, mid + 1, endIndex, target);}
变体实现:查找最后一个小于给定值的元素
还是最上面的那个数组,我们要查找最后一个小于等于8的元素,就是下标为4的元素。
public static int bSearchLastSmaller(int[] arr, int startIndex, int endIndex, int target) {// 递归推出条件if (startIndex > endIndex) {return -1;}// 取折中索引int mid = (startIndex + endIndex) / 2;// 折中值比较if (arr[mid] < target) {if (mid == endIndex || arr[mid + 1] >= target) {return mid;}return bSearchLastSmaller(arr, mid + 1, endIndex, target);}return bSearchLastSmaller(arr, startIndex, mid - 1, target);}
变体实现:查找第一个大于给定值的元素
还是最上面的那个数组,我们要查找最后一个大于等于8的元素,就是下标为8的元素。
public static int bSearchFirstBigger(int[] arr, int startIndex, int endIndex, int target) {// 递归推出条件if (startIndex > endIndex) {return -1;}// 取折中索引int mid = (startIndex + endIndex) / 2;// 折中值比较if (arr[mid] > target) {if (mid - 1 <= 0 || arr[mid - 1] <= target) {return mid;}return bSearchFirstBigger(arr, startIndex, mid - 1, target);}return bSearchFirstBigger(arr, mid + 1, endIndex, target);}
二分查找的局限性
-
首先,二分查找依赖的是顺序表结构,简单点说就是数组
二分查找能否依赖其他数据结构呢?比如链表。答案是不可以的,主要原因是二分查找算法需要按照下标随机访问元素。我们在数组和链表那两节讲过,数组按照下标随机访问数据的时间复杂度是 O(1),而链表随机访问的时间复杂度是 O(n)。所以,如果数据使用链表存储,二分查找的时间复杂就会变得很高。
二分查找只能用在数据是通过顺序表来存储的数据结构上。如果你的数据是通过其他数据结构存储的,则无法应用二分查找。 -
其次,二分查找针对的是有序数据
二分查找对这一点的要求比较苛刻,数据必须是有序的。如果数据没有序,我们需要先排序。前面章节里我们讲到,排序的时间复杂度最低是 O(nlogn)。所以,如果我们针对的是一组静态的数据,没有频繁地插入、删除,我们可以进行一次排序,多次二分查找。这样排序的成本可被均摊,二分查找的边际成本就会比较低。
但是,如果我们的数据集合有频繁的插入和删除操作,要想用二分查找,要么每次插入、删除操作之后保证数据仍然有序,要么在每次二分查找之前都先进行排序。针对这种动态数据集合,无论哪种方法,维护有序的成本都是很高的。
所以,二分查找只能用在插入、删除操作不频繁,一次排序多次查找的场景中。针对动态变化的数据集合,二分查找将不再适用。 -
再次,数据量太小不适合二分查找
如果要处理的数据量很小,完全没有必要用二分查找,顺序遍历就足够了。比如我们在一个大小为 10 的数组中查找一个元素,不管用二分查找还是顺序遍历,查找速度都差不多。只有数据量比较大的时候,二分查找的优势才会比较明显。
不过,这里有一个例外。如果数据之间的比较操作非常耗时,不管数据量大小,我都推荐使用二分查找。比如,数组中存储的都是长度超过 300 的字符串,如此长的两个字符串之间比对大小,就会非常耗时。我们需要尽可能地减少比较次数,而比较次数的减少会大大提高性能,这个时候二分查找就比顺序遍历更有优势。 -
最后,数据量太大也不适合二分查找
二分查找的底层需要依赖数组这种数据结构,而数组为了支持随机访问的特性,要求内存空间连续,对内存的要求比较苛刻。比如,我们有 1GB 大小的数据,如果希望用数组来存储,那就需要 1GB 的连续内存空间。
注意这里的“连续”二字,也就是说,即便有 2GB 的内存空间剩余,但是如果这剩余的 2GB 内存空间都是零散的,没有连续的 1GB 大小的内存空间,那照样无法申请一个 1GB 大小的数组。而我们的二分查找是作用在数组这种数据结构之上的,所以太大的数据用数组存储就比较吃力了,也就不能用二分查找了。
相关文章:

算法与数据结构-二分查找
文章目录 什么是二分查找二分查找的时间复杂度二分查找的代码实现简单实现:不重复有序数组查找目标值变体实现:查找第一个值等于给定值的元素变体实现:查找最后一个值等于给定值的元素变体实现:查找最后一个小于给定值的元素变体实…...

【软件测试】什么是selenium
1.seleniumJava环境搭建 前置条件: Java最低版本要求为8,浏览器使用chrome浏览器 1.1下载chrome浏览器 https://www.google.cn/chrome/ 1.2查看浏览器版本 点击关于Google chrome. 记住版本的前三个数. 1.3下载浏览器驱动 http://chromedriver.chromium.org/downloads 下载…...
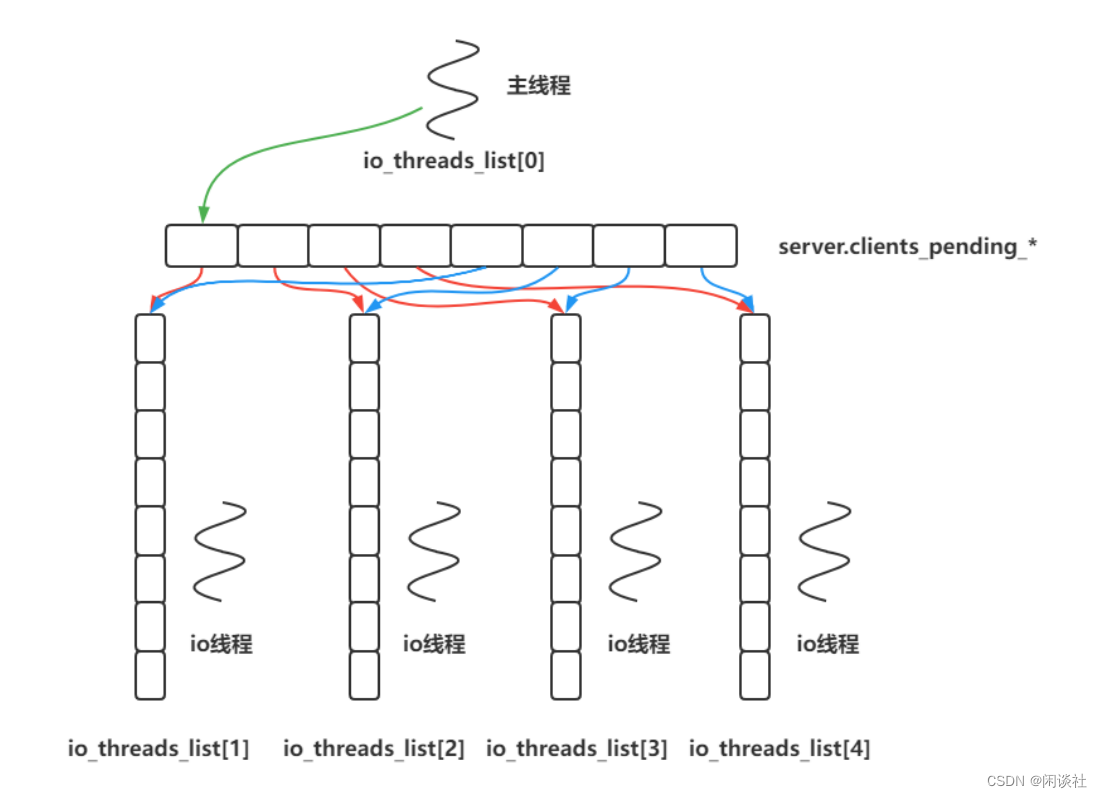
redis线程模型
文章目录 一、redis单线程模型1.1 为什么redis命令处理是单线程,而不采用多线程1.2 单线程的局限及redis的优化方式 二、redis单线程为什么这么快2.1 采用的机制2.2 优化的措施 三、redis的IO多线程模型3.1 redis 为什么引入IO多线程模型3.2 配置io-threads-do-read…...
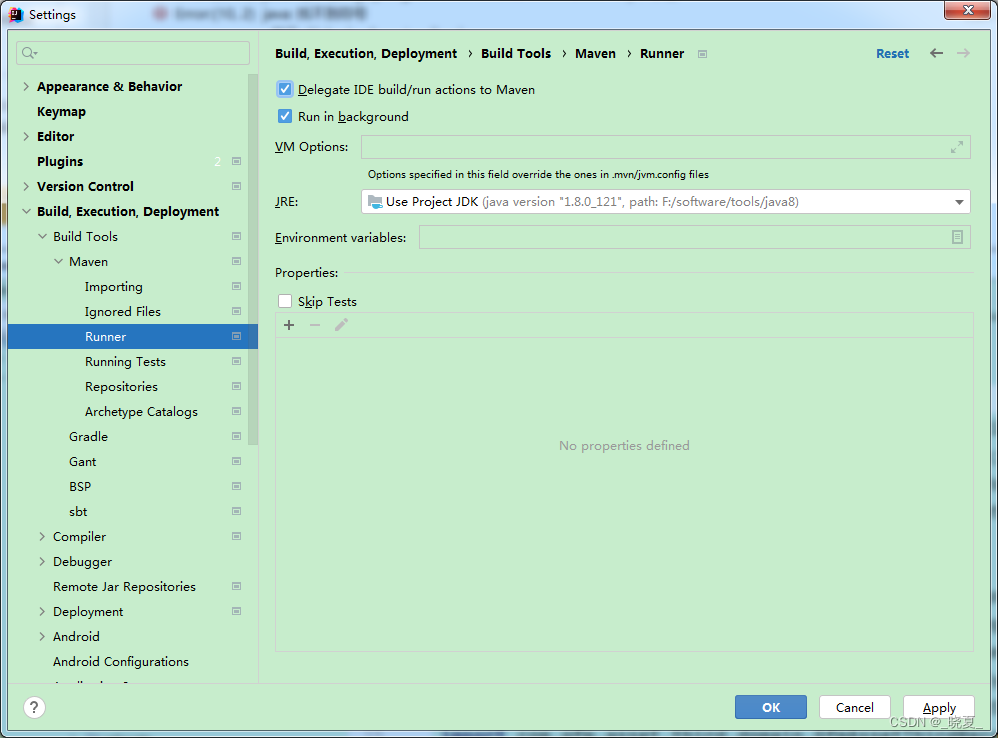
【idea工具】idea工具,build的时候提示:程序包 com.xxx.xx不存在的错误
idea工具,build的时候提示:程序包 com.xxx.xx不存在的错误,如下图,折腾了好一会, 做了如下操作还是不行,idea工具编译的时候,还是提示 程序包不存在。 a. idea中,重新导入项目,也还…...

线性代数——特征值和特征向量
系列文章目录 线性代数——行列式线性代数——矩阵线性代数——向量线性代数——线性方程组线性代数——特征值和特征向量线性代数——二次型 文章目录 系列文章目录版权声明补充知识求和公式的性质常用希腊字符读音 特征值和特征向量相似矩阵相似对角化实对称矩阵 版权声明 …...

运筹系列83:使用分枝定界求解tsp问题
1. 辅助函数 Node算子用来存储搜索树的状态。其中level等于path的长度,path是当前节点已经访问过的vertex清单,bound则是当前的lb。 这里的bound函数是一种启发式方法,等于当前路径的总长度,再加上往后走两步的最小值。 struct …...
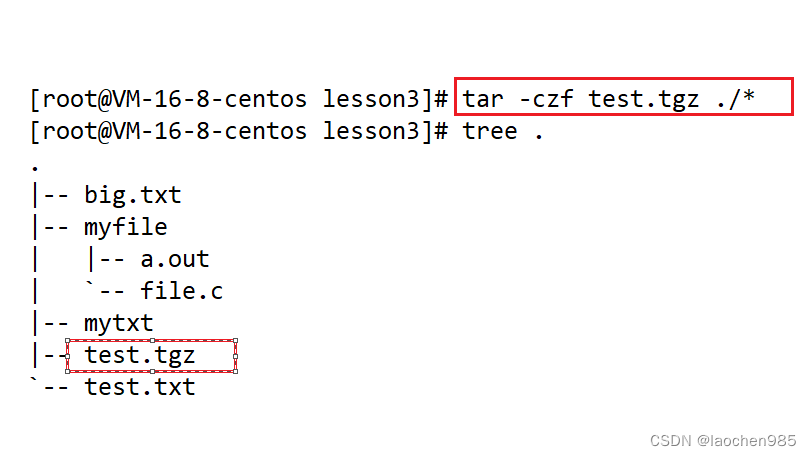
linux 指令 第3期
cat cat 指令: 首先我们知道一个文件内容属性 我们对文件操作就有两个方面:对文件内容和属性的操作 扩展:echo 指令 直接打印echo后面跟的字符串 看: 这其实是把它打印到了显示器上,我们也可以改变一下它的打印位置…...
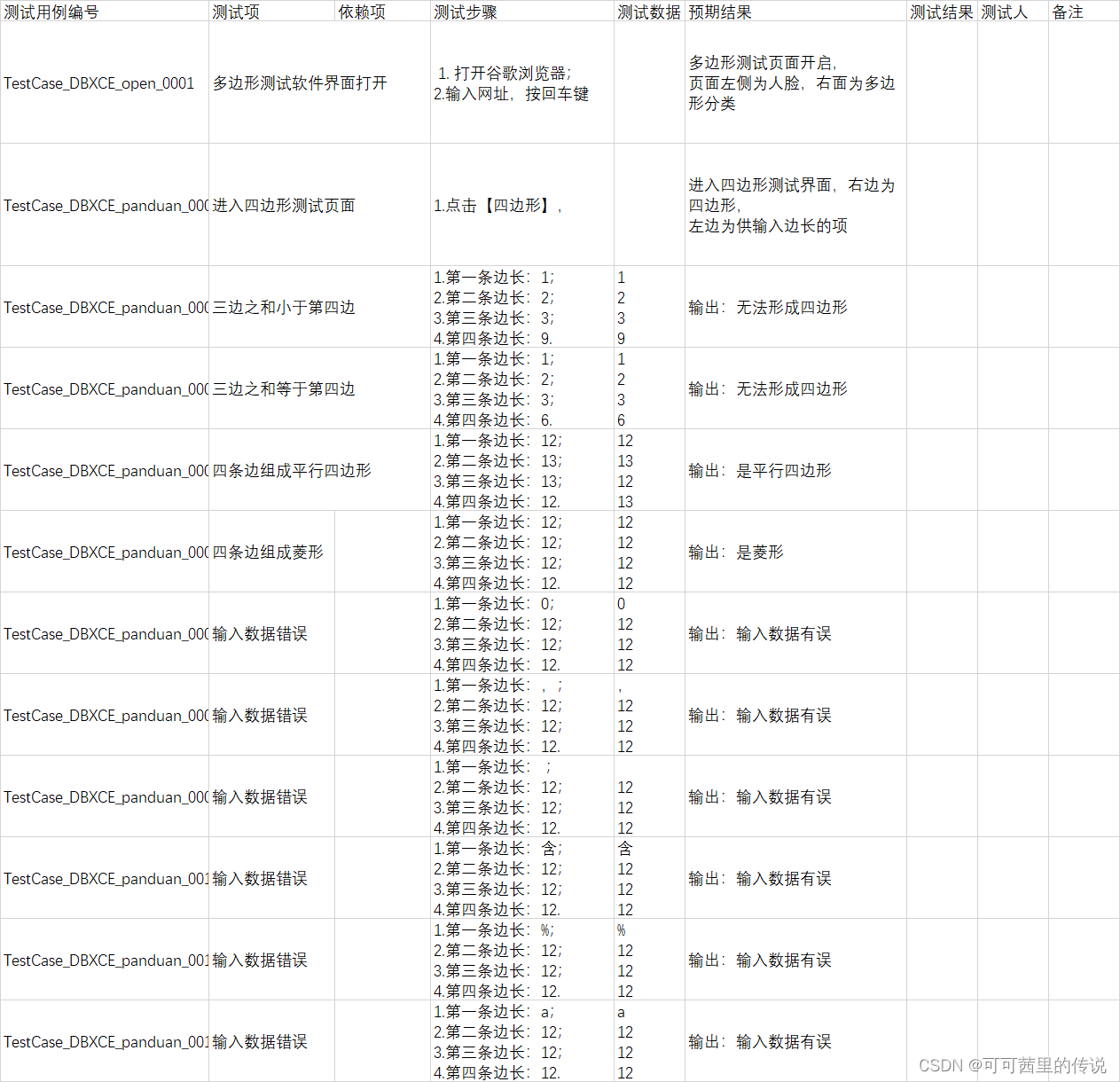
测试用例实战
测试用例实战 三角形判断 三角形测试用例设计 测试用例编写 先做正向数据,再做反向数据。 只要有一条边长为0,那就是不符合要求,不需要再进行判断,重复。 四边形 四边形测试用例...

Unity XML1——XML基本语法
一、XML 概述 全称:可拓展标记语言(EXtensible Markup Language) XML 是国际通用的,它是被设计来用于传输和存储数据的一种文本特殊格式,文件后缀一般为 .xml 我们在游戏中可以把游戏数据按照 XML 的格式标…...

了解Unity编辑器之组件篇Playables和Rendering(十)
Playables 一、Playable Director:是一种用于控制和管理剧情、动画和音频的工具。它作为一个中央控制器,可以管理播放动画剧情、视频剧情和音频剧情,以及它们之间的时间、顺序和交互。 Playable Director组件具有以下作用: 剧情控…...
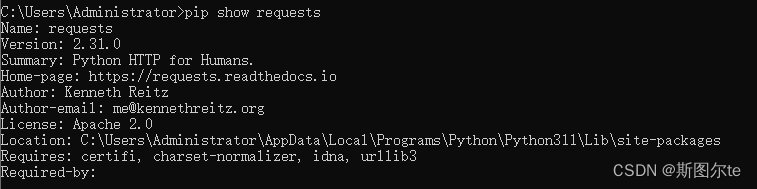
python的包管理器pip安装经常失败的解决办法:修改pip镜像源
pip 常用的国内镜像源: https://pypi.tuna.tsinghua.edu.cn/simple/ // 清华 http://mirrors.aliyun.com/pypi/simple/ // 阿里云 https://pypi.mirrors.ustc.edu.cn/simple/ // 中国科技大学 http://pypi.hustunique.com/ // 华中理…...
忘记安卓图案/密码锁如何解锁?
如何解锁Android手机图案锁?如何删除忘记的密码?Android 手机锁定后如何重置?这是许多智能手机用户在网上提出的几个问题。为了回答这些问题,我们想出了一些简单有效的方法来解锁任何设备而不丢失数据。 忘记手机密码可能会令人恐…...
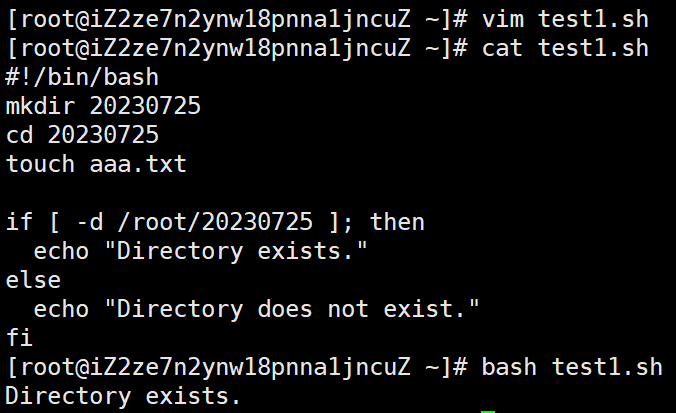
Bash编程
目录: bash编程语法bash脚本编写 1.bash编程语法 Bash 编程基础 变量引号数组控制语句函数 Bash 变量 语法: Variable_namevalue Bash 变量定义的规则 变量名区分大小写,a和A为两个不同的变量。变量名可以使用大小写字母混编的形式进行…...

vue指令-v-model修饰符
vue指令-v-model修饰符 1、目标2、语法 1、目标 让v-modelv-mode拥有更强大的功能 2、语法 v-model.修饰符“Vue数据变量” .number 以parseFloat转成数字类型 .trime 去除首位空白字符 .lazy 在change时触发而非input时示例1 <template><div id"app"&g…...

【论文精读CVPR_2023】3D-Aware Face Swapping
【论文精读CVPR_2023】3D-Aware Face Swapping 前言Abstract1. Introduction2. Related WorkFace Swapping.3D-Aware Generative Models.GAN Inversion.3. Method3.1. Overview3.2. Inferring 3D Prior from 2D Images3.3. Face Swapping via Latent Code Manipulation3.4. Joi…...

flutter开发实战-自定义相机camera功能
flutter开发实战-自定义相机camera功能。 Flutter 本质上只是一个 UI 框架,运行在宿主平台之上,Flutter 本身是无法提供一些系统能力,比如使用蓝牙、相机、GPS等,因此要在 Flutter 中调用这些能力就必须和原生平台进行通信。 实现…...

重排链表——力扣143
文章目录 题目描述法一:寻找链表中点、链表逆序、链表合并 题目描述 法一:寻找链表中点、链表逆序、链表合并 void reorderList(ListNode* head){if(headnullptr){return;}// 找到中点 ListNode* mid FindMiddle(head);ListNode *h1head, *h2mid->ne…...
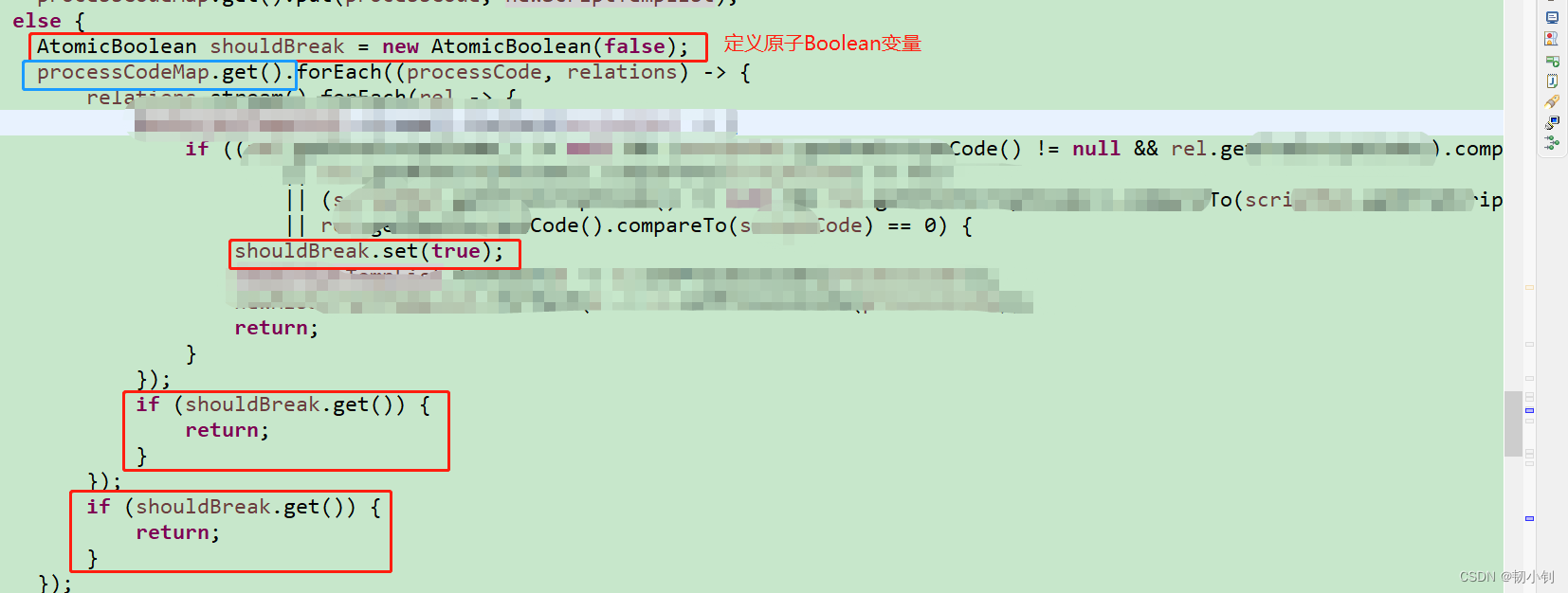
Lambda表达式常见的Local variable must be final or effectively final原因及解决办法
目录 Local variable must be final or effectively final错误原因 解决办法按照要求定义为final(不符合实情,很多时候是查库获取的变量值)使用原子类存储变量,保证一致性AtomicReference常用原子类 其它 Local variable must be …...

YOLOv5改进系列(16)——添加EMA注意力机制(ICASSP2023|实测涨点)
【YOLOv5改进系列】前期回顾: YOLOv5改进系列(0)——重要性能指标与训练结果评价及分析 YOLOv5改进系列(1)——添加SE注意力机制 YOLOv5改进系列(2)——添加...
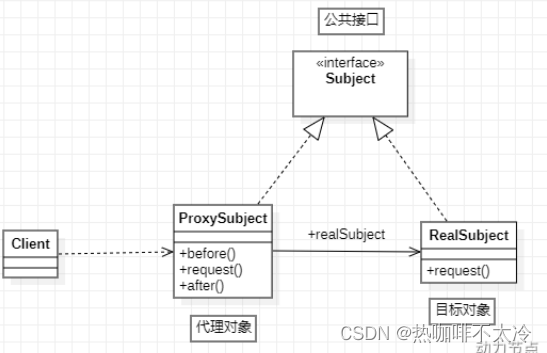
[SSM]GoF之代理模式
目录 十四、GoF之代理模式 14.1对代理模式的理解 14.2静态代理 14.3动态代理 14.3.1JDK动态代理 14.3.2CGLIB动态代理 十四、GoF之代理模式 14.1对代理模式的理解 场景:拍电影的时候,替身演员去代理演员完成表演。这就是一个代理模式。 演员为什…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...

TCP/IP 网络编程 | 服务端 客户端的封装
设计模式 文章目录 设计模式一、socket.h 接口(interface)二、socket.cpp 实现(implementation)三、server.cpp 使用封装(main 函数)四、client.cpp 使用封装(main 函数)五、退出方法…...

算法刷题-回溯
今天给大家分享的还是一道关于dfs回溯的问题,对于这类问题大家还是要多刷和总结,总体难度还是偏大。 对于回溯问题有几个关键点: 1.首先对于这类回溯可以节点可以随机选择的问题,要做mian函数中循环调用dfs(i&#x…...

【大厂机试题解法笔记】矩阵匹配
题目 从一个 N * M(N ≤ M)的矩阵中选出 N 个数,任意两个数字不能在同一行或同一列,求选出来的 N 个数中第 K 大的数字的最小值是多少。 输入描述 输入矩阵要求:1 ≤ K ≤ N ≤ M ≤ 150 输入格式 N M K N*M矩阵 输…...

前端打包工具简单介绍
前端打包工具简单介绍 一、Webpack 架构与插件机制 1. Webpack 架构核心组成 Entry(入口) 指定应用的起点文件,比如 src/index.js。 Module(模块) Webpack 把项目当作模块图,模块可以是 JS、CSS、图片等…...
