Minimum Snap闭式求解相关公式推导
文章目录
- 1 M i n i m u m Minimum Minimum S n a p Snap Snap闭式求解的推导
- 1.1 二次规划等式约束构建
- 1.2 求 d d d
- 1.3 转成无约束优化问题
1 M i n i m u m Minimum Minimum S n a p Snap Snap闭式求解的推导
可以看看我的这几篇Blog1,Blog2,Blog3。
1.1 二次规划等式约束构建
闭式法中的 Q Q Q 矩阵计算和之前 M i n i m u m Minimum Minimum S n a p Snap Snap当中的一样,但约束的形式与之前略为不同,在之前的方法中, 等式约束只要构造成 [ … ] p = b [\ldots] p=b […]p=b 的形式就可以了,而闭式法中,每段轨迹都构造成如下:
A i p i = d i , A i = [ A 0 A t ] i T , d i = [ d 0 , d T ] i A_{i} p_{i}=d_{i}, A_{i}=\left[A_{0} A_{t}\right]_{i}^{T}, d_{i}=\left[d_{0}, d_{T}\right]_{i} Aipi=di,Ai=[A0At]iT,di=[d0,dT]i
其中 d 0 、 d T d_{0}、d_{T} d0、dT 为第 i i i 段轨迹的起点和终点的各阶导数组成的向量,比如只考虑PVA: d 0 = [ p 0 , v 0 , a 0 ] T d_{0}=\left[p_{0}, v_{0}, a_{0}\right]^{T} d0=[p0,v0,a0]T , 当然也可以把 j e r k 、 s n a p jerk、snap jerk、snap等加入到向量。注意:这里是不管每段端点的 P V A PVA PVA是否已知,都写进来。 块合并各段轨迹的约束方程得到:
A t o t a l [ p 1 ⋮ p k ] = [ d 1 ⋮ d k ] = [ p 1 ( t 0 ) v 1 ( t 0 ) a 1 ( t 0 ) p 1 ( t 1 ) v 1 ( t 1 ) a 1 ( t 1 ) ⋮ p k ( t k − 1 ) v k ( t k − 1 ) a k ( t k − 1 ) p k ( t k ) v k ( t k ) a k ( t k ) ] ⏟ 6 k × 1 A_{total}\left[\begin{array}{c} p_{1} \\ \vdots \\ p_{k} \end{array}\right]=\left[\begin{array}{c} d_{1} \\ \vdots \\ d_{k} \end{array}\right]=\underbrace{\left[\begin{array}{c} p_{1}\left(t_{0}\right) \\ v_{1}\left(t_{0}\right) \\ a_{1}\left(t_{0}\right) \\ p_{1}\left(t_{1}\right) \\ v_{1}\left(t_{1}\right) \\ a_{1}\left(t_{1}\right) \\ \vdots \\ p_{k}\left(t_{k-1}\right) \\ v_{k}\left(t_{k-1}\right) \\ a_{k}\left(t_{k-1}\right) \\ p_{k}\left(t_{k}\right) \\ v_{k}\left(t_{k}\right) \\ a_{k}\left(t_{k}\right) \end{array}\right]}_{6 k \times 1} Atotal p1⋮pk = d1⋮dk =6k×1 p1(t0)v1(t0)a1(t0)p1(t1)v1(t1)a1(t1)⋮pk(tk−1)vk(tk−1)ak(tk−1)pk(tk)vk(tk)ak(tk)
k k k 为轨迹段数, n n n 为轨迹的阶数,设只考虑pva, A total A_{\text {total }} Atotal 的 s i z e size size为 ( n order + 1 ) k × 6 k \left(n_{\text {order }}+1\right) k \times 6 k (norder +1)k×6k 。
由上式可以看到, A total A_{\text {total }} Atotal 是已知的 ,而 d d d 中只有少部分(起点、终点的 P V A PVA PVA等)是已知的,其他大部分是未知的。如果能够求出 d \boldsymbol{d} d ,那么轨迹参数可以通过 p = A − 1 d p=A^{-1} d p=A−1d 很容易求得。
1.2 求 d d d
闭式法的思路是: 将 d d d 向量中的变量分成两部分:" d d d中所有已知量组成的 F i x Fix Fix部分 d F d_{F} dF "和”所有末知量组成的 F r e e Free Free部分 d P d_{P} dP ”。然后通过推导,根据 d F d_{F} dF 求得 d P d_{P} dP ,从而得到 d d d ,最后求得 p p p 。 下面介绍整个推导过程。
消除重复变量(连续性约束)
可以会发现,上面构造等式约束时,并没有加入连续性约束,连续性约束并不是直接加到等式约束中。 考虑到连续性 (这里假设PVA连续), d d d 向量中很多变量其实重复了,即
p i ( t i ) = p i + 1 ( t i ) , v i ( t i ) = v i + 1 ( t i ) , a i ( t i ) = a i + 1 ( t i ) p_{i}\left(t_{i}\right)=p_{i+1}\left(t_{i}\right), \quad v_{i}\left(t_{i}\right)=v_{i+1}\left(t_{i}\right), \quad a_{i}\left(t_{i}\right)=a_{i+1}\left(t_{i}\right) pi(ti)=pi+1(ti),vi(ti)=vi+1(ti),ai(ti)=ai+1(ti)
因此需要一个映射矩阵将一个变量映射到两个重复的变量上,如 [ a a ] = [ 1 1 ] a \left[\begin{array}{l}a \\ a\end{array}\right]=\left[\begin{array}{l}1 \\ 1\end{array}\right] a [aa]=[11]a ,将变量 a a a 映射到左边向量中的两个变量。
所以构造映射矩阵 M 6 k × 3 ( k + 1 ) M_{6 k \times 3(k+1)} M6k×3(k+1) :即 d = M d ′ d=M d^{\prime} d=Md′ 。
向量元素置换
消除掉重复变量之后,需要调整 d ′ d^{\prime} d′ 中的变量,把fix部分和free部分分开排列,可以左成一个置换矩阵 C C C ,使得
d ′ = C [ d F d P ] d^{\prime}=C\left[\begin{array}{l} d_{F} \\ d_{P} \end{array}\right] d′=C[dFdP]
再来构造 C C C矩阵即可, C C C阵的构造参考 M i n i m u m Minimum Minimum S n a p Snap Snap的构造方法,例如设 d ′ = [ a b c d ] d^{\prime}=\left[\begin{array}{l}a \\ b \\ c \\ d\end{array}\right] d′= abcd , 其中 a , c , d a, c, d a,c,d 是已知 ( d F ) , b \left(d_{F}\right) , b (dF),b 末知 ( d P ) \left(d_{P}\right) (dP) ,构造一个 4 × 4 4 \times 4 4×4 的单位阵,取 d F d_{F} dF 所在的 ( 1 , 3 , 4 ) (1,3,4) (1,3,4) 列放到左边,再取 d P \boldsymbol{d}_{P} dP 所在的 ( 2 ) (2) (2)列放到右边,就构造出置换矩阵 C \boldsymbol{C} C :
[ a b c d ] = [ 1 0 0 0 0 0 0 1 0 1 0 0 0 0 1 0 ] ⏟ C [ a c d b ] \left[\begin{array}{l} a \\ b \\ c \\ d \end{array}\right]=\underbrace{\left[\begin{array}{llll} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array}\right]}_{C}\left[\begin{array}{l} a \\ c \\ d \\ b \end{array}\right] abcd =C 1000001000010100 acdb
1.3 转成无约束优化问题
由上面两步可得
d = M C [ d F d P ] p = A − 1 d = A − 1 M C ⏟ K [ d F d P ] = K [ d F d P ] \begin{gathered} d=M C\left[\begin{array}{l} d_{F} \\ d_{P} \end{array}\right] \\ p=A^{-1} d=\underbrace{A^{-1} M C}_{K}\left[\begin{array}{l} d_{F} \\ d_{P} \end{array}\right]=K\left[\begin{array}{l} d_{F} \\ d_{P} \end{array}\right] \end{gathered} d=MC[dFdP]p=A−1d=K A−1MC[dFdP]=K[dFdP]
代入优化函数:
min J = p T Q p J = [ d F d P ] T K T Q K ⏟ R [ d F d P ] = [ d F d P ] T [ R F F R F P R P F R P P ] [ d F d P ] = d F T R F F d F + d F T R F P d P + d P T R P F d F + d P T R P P d P Q 对称 ⇒ R 对称 ⇒ ⇒ = d F T R F F d F + 2 d F T R F P d P + d P T R P P d P \begin{aligned} \min J &=p^{T} Q p \\ J &=\left[\begin{array}{l} d_{F} \\ d_{P} \end{array}\right]^{T} \underbrace{K^{T} Q K}_{R}\left[\begin{array}{l} d_{F} \\ d_{P} \end{array}\right] \\ &=\left[\begin{array}{l} d_{F} \\ d_{P} \end{array}\right]^{T}\left[\begin{array}{ll} R_{F F} & R_{F P} \\ R_{P F} & R_{P P} \end{array}\right]\left[\begin{array}{l} d_{F} \\ d_{P} \end{array}\right] \\ &=d_{F}^{T} R_{F F} d_{F}+d_{F}^{T} R_{F P} d_{P}+d_{P}^{T} R_{P F} d_{F}+d_{P}^{T} R_{P P} d_{P} \\ Q_{\text {对称 } \Rightarrow R \text { 对称 } \Rightarrow} \Rightarrow &=d_{F}^{T} R_{F F} d_{F}+2 d_{F}^{T} R_{F P} d_{P}+d_{P}^{T} R_{P P} d_{P} \end{aligned} minJJQ对称 ⇒R 对称 ⇒⇒=pTQp=[dFdP]TR KTQK[dFdP]=[dFdP]T[RFFRPFRFPRPP][dFdP]=dFTRFFdF+dFTRFPdP+dPTRPFdF+dPTRPPdP=dFTRFFdF+2dFTRFPdP+dPTRPPdP
令 J J J 对 d P d_{P} dP 的导数 ∂ J ∂ d P = 0 \frac{\partial J}{\partial d_{P}}=0 ∂dP∂J=0 求极值点:
⇒ 2 d F T R F P + 2 d P T R P P d P = 0 (注意 R P P T = R P P ) ⇒ d p = − R P P − 1 R F P T d F \begin{gathered} \Rightarrow 2 d_{F}^{T} R_{F P}+2 d_{P}^{T} R_{P P} d_{P}=0 \text { (注意 } R_{P P}^{T}=R_{P P} \text { ) } \\ \Rightarrow d_{p}=-R_{P P}^{-1} R_{F P}^{T} d_{F} \end{gathered} ⇒2dFTRFP+2dPTRPPdP=0 (注意 RPPT=RPP ) ⇒dp=−RPP−1RFPTdF
至此求得 d P d_{P} dP ,从而求出 p p p 。
相关文章:

Minimum Snap闭式求解相关公式推导
文章目录 1 M i n i m u m Minimum Minimum S n a p Snap Snap闭式求解的推导1.1 二次规划等式约束构建1.2 求 d d d1.3 转成无约束优化问题 1 M i n i m u m Minimum Minimum S n a p Snap Snap闭式求解的推导 可以看看我的这几篇Blog1,Blog2,Blog…...
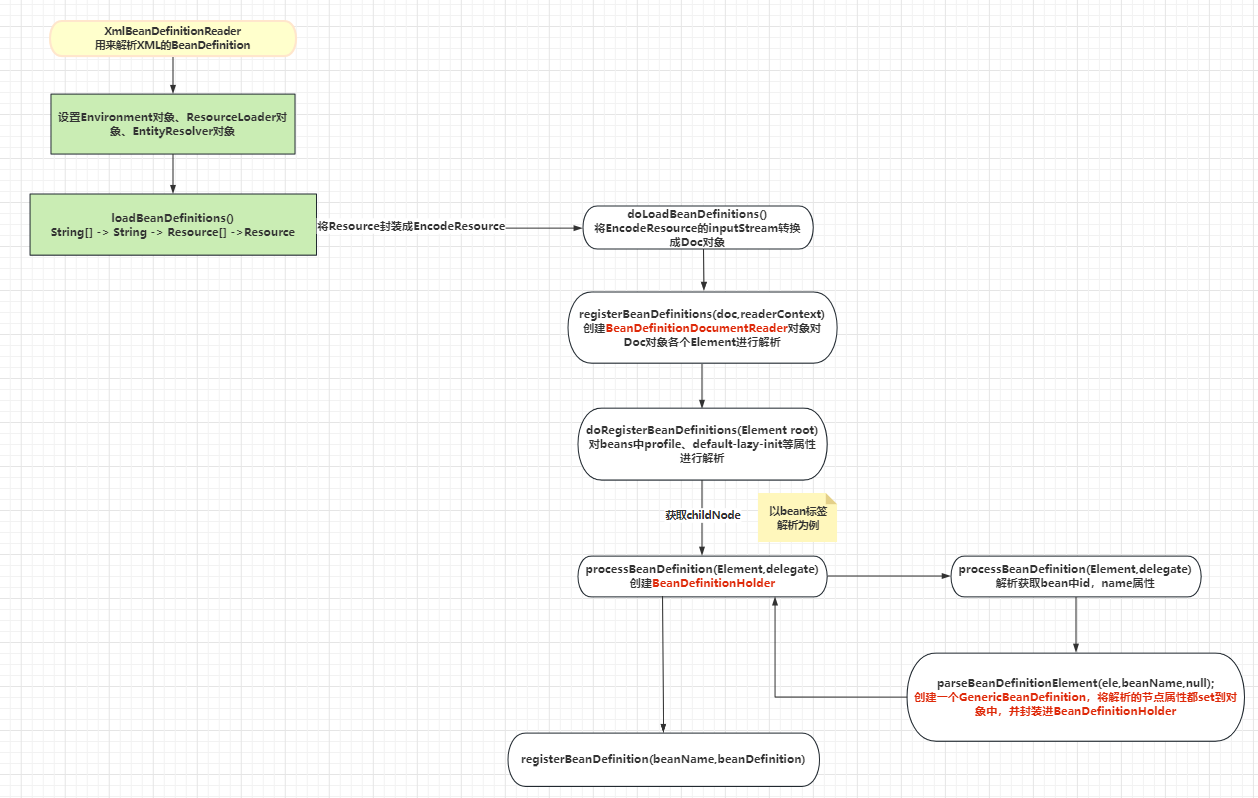
Spring源码(五)— 解析XML配置文件(一) bean标签解析流程
前面几章的内容已经介绍了BeanFactory创建前的准备工作,以及加载XML配置文件前的准备的步骤。本章会着重介绍解析XML的步骤。 registerBeanDefinitions 前几个方法不做过多的赘述,着重看registerBeanDefinitions方法中解析XML的步骤。 public int regi…...

隐私政策声明
http://lxfamn.cn/tools 我们注重对您个人隐私的保护。有时候我们需要某些信息才能为您提供您请求的服务,本隐私声明解释了这些情况下的数据收集和使用情况。本隐私声明适用于本网站的所有相关服务。如果您访问本网站、使用本网站的任何服务,那么您便接受…...

Flutter 最佳实践和编码准则
Flutter 最佳实践和编码准则 视频 前言 最佳实践是一套既定的准则,可以提高代码质量、可读性和可靠性。它们确保遵循行业标准,鼓励一致性,并促进开发人员之间的合作。通过遵循最佳实践,代码变得更容易理解、修改和调试ÿ…...
LangChain Agents深入剖析及源码解密上(一)
LangChain Agents深入剖析及源码解密上(一) LangChain Agents深入剖析及源码解密上 Agent工作原理详解 本节会结合AutoGPT的案例,讲解LangChain代理(Agent)为核心的内容。我们前面已经谈了代理本身的很多内容,也看了绝大部分的源代码,例如:ReAct的源代码,还有mrkl的源代…...
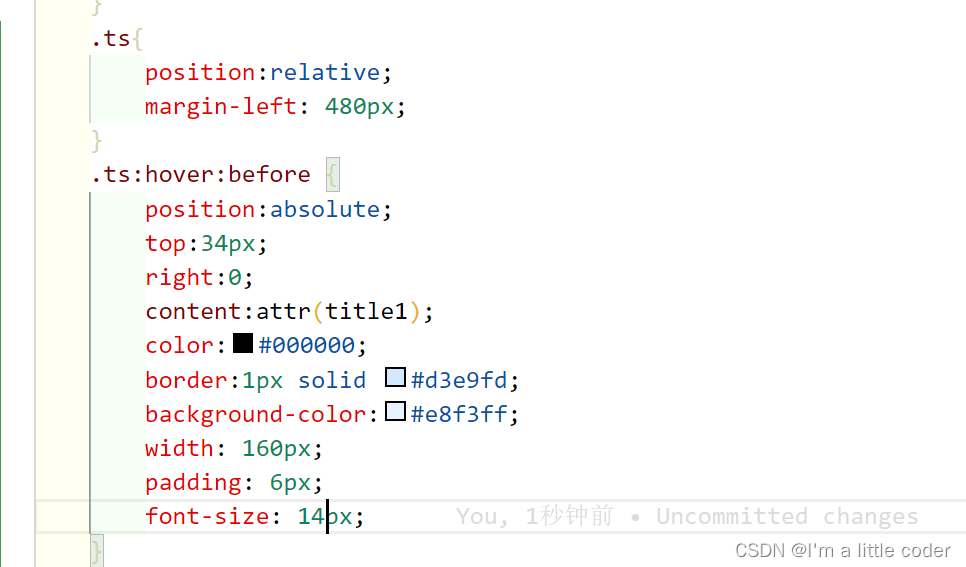
css定义超级链接a标签里面的title的样式
效果: 代码: 总结:此css 使用于任何元素,不仅仅是a标签!...
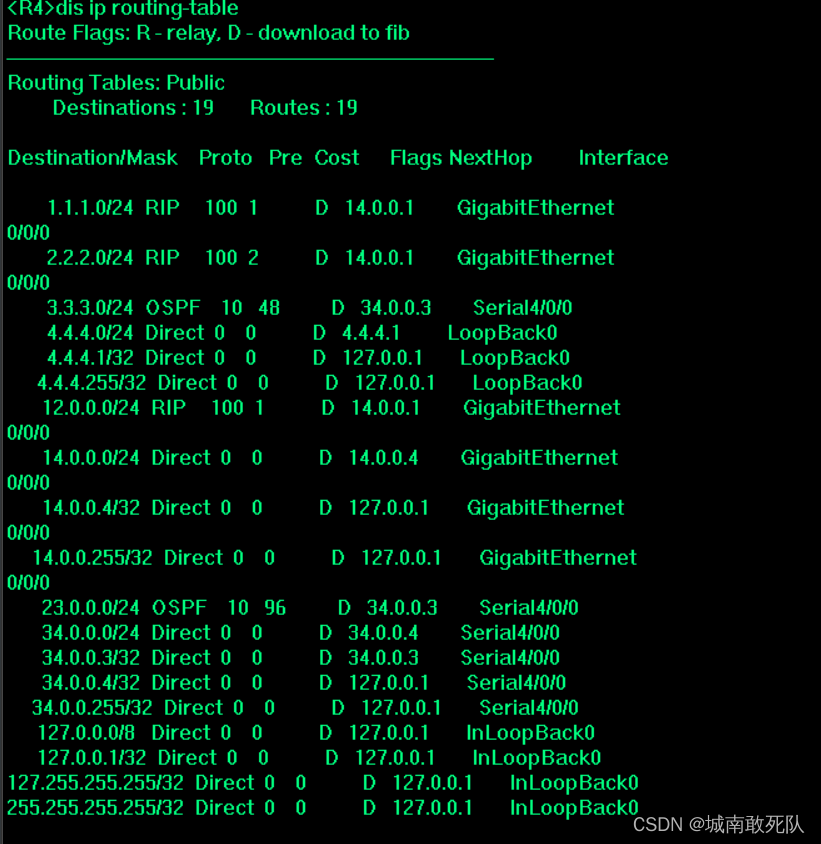
hcip——路由策略
要求: 基础配置 AR1 [R1]int g 0/0/0 [R1-GigabitEthernet0/0/0]ip add 12.0.0.1 24[R1-GigabitEthernet0/0/0]int g 0/0/1 [R1-GigabitEthernet0/0/1]ip add 14.0.0.1 24[R1]int loop0 [R1-LoopBack0]ip add 1.1.1.1 24[R1]rip 1 [R1-rip-1]vers 2 [R1-rip-1]net…...
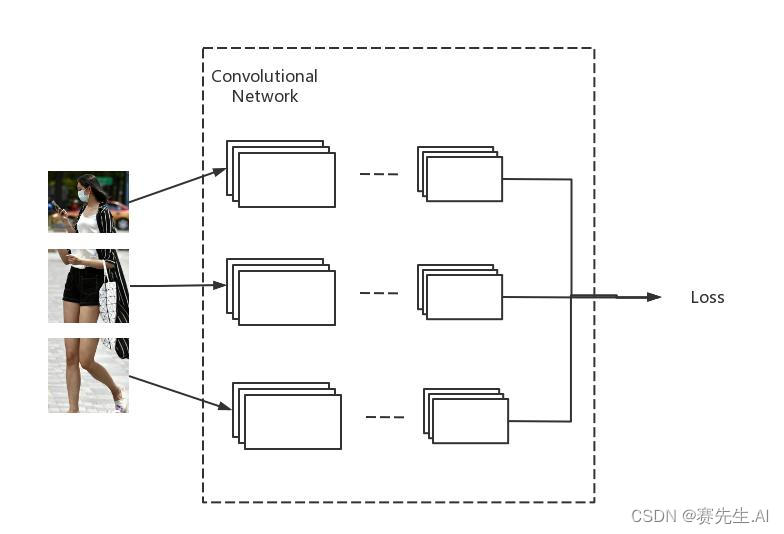
ReID网络:MGN网络(1) - 概述
Start MGN 1. 序言 现代基于感知的信息中,视觉信息占了80~85%。基于视觉信息的处理和分析被应用到诸如安防、电力、汽车等领域。 以安防市场为例,早在2017年,行业咨询公司IHS Market,我国在公共和私人领域安装有摄像头约1.76亿…...
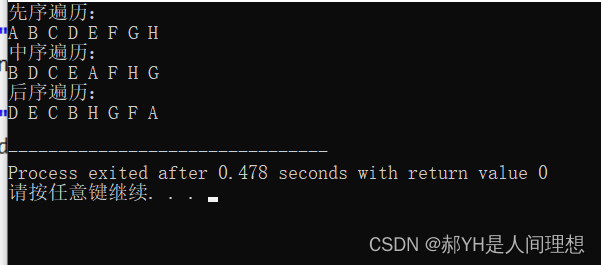
C++数据结构笔记(10)递归实现二叉树的三序遍历
对于三种遍历方式来说,均为先左后右!区别在于根结点的位置顺序 先序遍历:根——左——右 中序遍历:左——根——右 后序遍历:左——右——根 (所谓先中后的顺序,是指根结点D先于子树还是后于…...
hMailServer-5.3.3-B1879.exe
hMailServer-5.3.3-B1879.exe...

后端校验JSR303
目录 一、导入依赖 二、实现步骤 三、分组校验 四、自定义校验 一、导入依赖 <dependency><groupId>javax.validation</groupId><artifactId>validation-api</artifactId><version>2.0.1.Final</version></dependency> 二…...

vmware磁盘组使用率100%处理
今天在外办事时,有客户发过来一个截图,问vmware 磁盘组空间使用率100%咋办?如下图: 直接回复: 1、首先删除iso文件等 2、若不存在ISO文件等,找个最不重要的虚拟机直接删除,删除后稍等就会释放…...
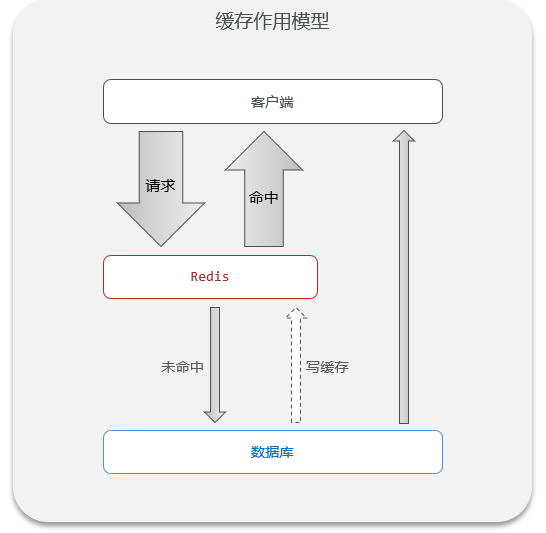
Redis实战(3)——缓存模型与缓存更新策略
1 什么是缓存? 缓存就是数据交换的缓冲区, 是存贮数据的临时区,一般读写性能较高 \textcolor{red}{是存贮数据的临时区,一般读写性能较高} 是存贮数据的临时区,一般读写性能较高。缓存可在多个场景下使用 以一次 w e b 请求为例…...

python与深度学习(十):CNN和cifar10二
目录 1. 说明2. cifar10的CNN模型测试2.1 导入相关库2.2 加载数据和模型2.3 设置保存图片的路径2.4 加载图片2.5 图片预处理2.6 对图片进行预测2.7 显示图片 3. 完整代码和显示结果4. 多张图片进行测试的完整代码以及结果 1. 说明 本篇文章是对上篇文章训练的模型进行测试。首…...
剑指offer12 矩阵中的路径 13 机器人的运动范围 34.二叉树中和为某一值得路径
class Solution { public:bool exist(vector<vector<char>>& board, string word) {int rowboard.size(),colboard[0].size();int index0,i0,j0;if(word.size()>row*col) return 0;//vector<vector<int>> visit[row][col];//标记当前位置有没有…...

Pushgateway+Prometheus监控Flink
思路方案 FlinkMtrics->pushgateway->prometheus->grafnana->altermanager 方案 : Flink任务先将数据推到pushgateway。然后pushgateway将值推送到prometheus,最后grafana展示prometheus中的值, 去这个 https://prometheus.io/download/ 下载最新的 Prometheu…...
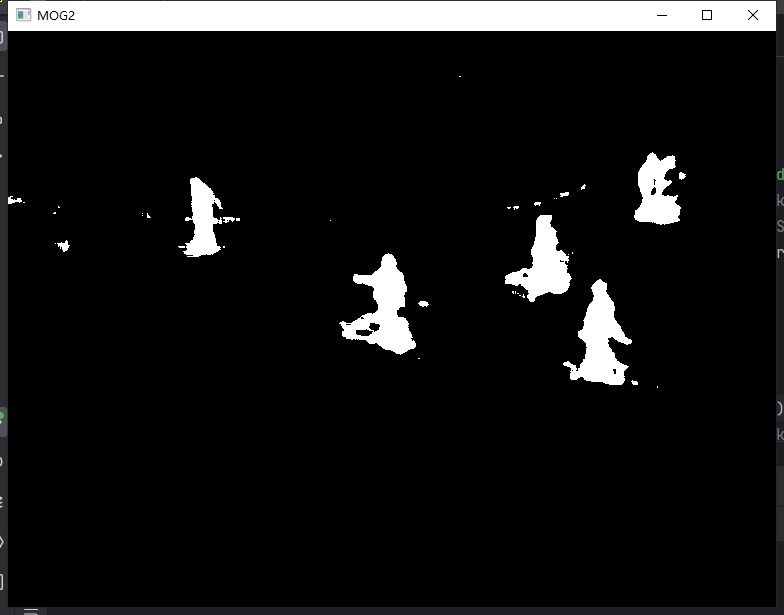
OpenCV图像处理-视频分割静态背景-MOG/MOG2/GMG
视频分割背景 1.概念介绍2. 函数介绍MOG算法MOG2算法GMG算法 原视频获取链接 1.概念介绍 视频背景扣除原理:视频是一组连续的帧(一幅幅图组成),帧与帧之间关系密切(GOP/group of picture),在GOP中,背景几乎…...

nginx 反向代理浅谈
前言 通常情况下,客户端向Web服务器发送请求,Web服务器响应请求并返回数据。而在反向代理中,客户端的请求不直接发送到Web服务器,而是发送到反向代理服务器。反向代理服务器会将请求转发给真实的Web服务器,Web服务器响…...
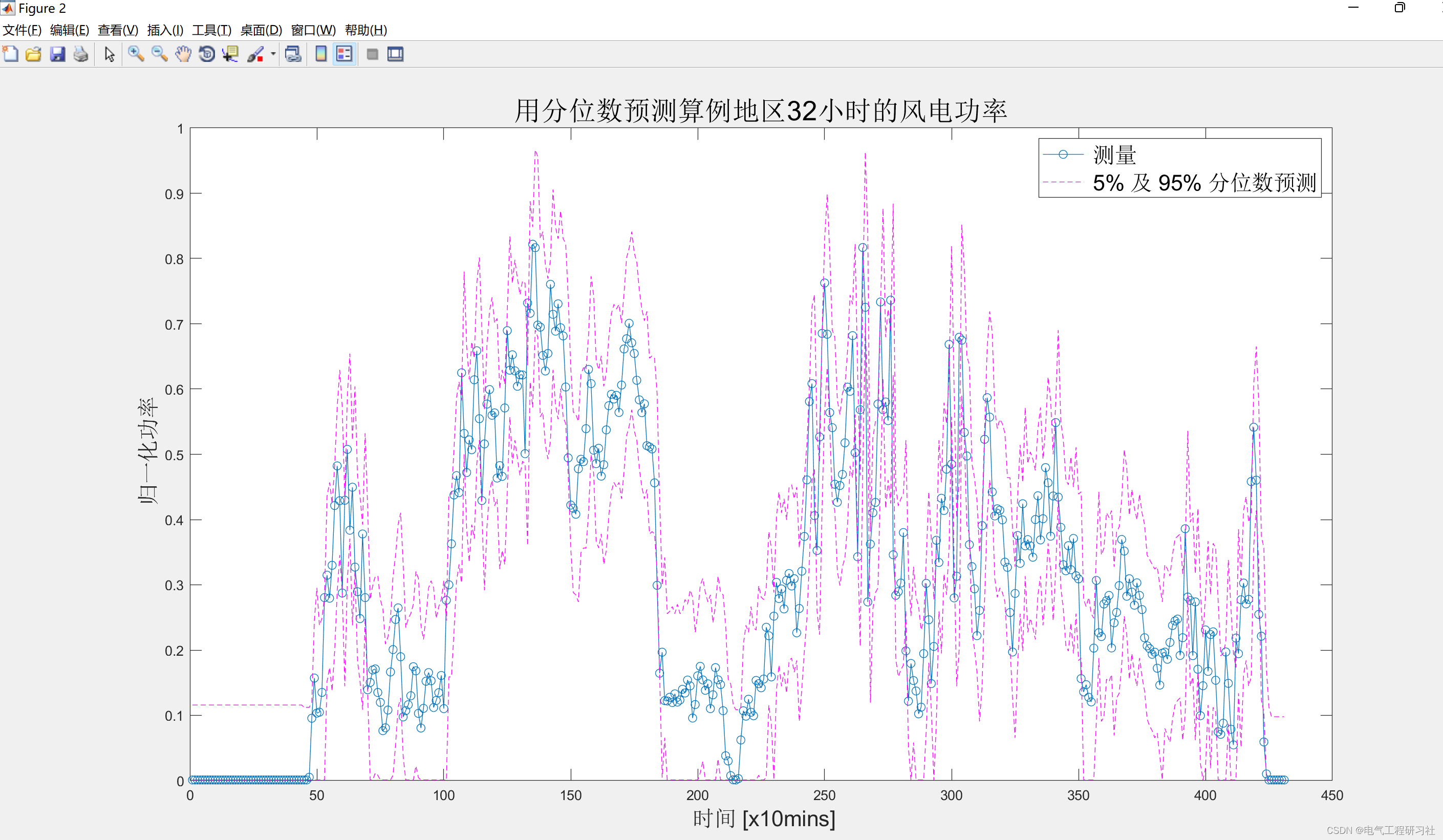
【概率预测】对风力发电进行短期概率预测的分析研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

原型设计模式go实现尝试
文章目录 前言代码结果总结 前言 本文章尝试使用go实现“原型”。 代码 package mainimport ("fmt" )// 不同原型标志枚举 type Type intconst (PROTOTYPE_1 Type iotaPROTOTYPE_2 )// 原型接口 type IPrototype interface {Clone() IPrototypeMethod(value int)P…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...
