【图论】Prim算法
一.介绍
![]()
Prim算法是一种用于解决最小生成树问题的贪心算法。最小生成树问题是指在一个连通无向图中找到一个生成树,使得树中所有边的权重之和最小。
Prim算法的基本思想是从一个起始顶点开始,逐步扩展生成树,直到覆盖所有顶点。具体步骤如下:
- 选择一个起始顶点作为生成树的根节点,并将其加入生成树中。
- 从生成树中的顶点出发,选择一条与生成树相连的边中权重最小的边,并将其加入生成树中。
- 重复步骤2,直到生成树包含了所有顶点。
Prim算法的关键在于如何选择与生成树相连的边中权重最小的边。一种常用的方法是使用优先队列(最小堆)来存储候选边,每次选择权重最小的边加入生成树。
Prim算法的时间复杂度为O(ElogV),其中V是顶点数,E是边数。它是一种有效的算法,适用于稠密图和稀疏图。
二.Prim与Dijkstra
其实Prim算法和Dijkstra算法差不多,就是一点小的改进,分别在第29,32,33行。
29:统计sum数量,若sum<n,说明无法构成最小树,因为构成最小树的点都不够!
32,33:w<dis[v]即可,因为只需要点到点,不是点到起点.
三.题目:
P3366 【模板】最小生成树 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
四.【AC】代码
#include<bits/stdc++.h>
#define maxn 200005
#define inf 0x7fffffff
using namespace std;
int n,m,ans=0,sum=0;
int head[5001],dis[5001];
bool vis[maxn],flag=0;
//链式前向星
struct Edge{int u,v,w,next;
}edge[maxn<<1]; //无向图,要*2
int cnt=0;
void add(int u,int v,int w){edge[++cnt]=(Edge){u,v,w,head[u]};head[u]=cnt;
}
struct node{int u,w;bool operator < (const node &x) const{return x.w<w;}
};
void Prim(){for(int i=2;i<=n;i++) dis[i]=inf;dis[1]=0;priority_queue<node> q;q.push((node){1,0});while(!q.empty()){node temp=q.top();q.pop();int u=temp.u;if(vis[u]) continue;vis[u]=1;sum++;ans+=temp.w;for(int i=head[u];i;i=edge[i].next){int v=edge[i].v,w=edge[i].w;if(w<dis[v]){dis[v]=w;q.push((node){v,dis[v]});}}}
}
int main(){//输入数据 cin>>n>>m;for(int i=1;i<=m;i++){int u,v,w;cin>>u>>v>>w;add(u,v,w);add(v,u,w);}//调用算法 Prim();//输出答案if(sum==n) cout<<ans;else cout<<"orz"; return 0;
}相关文章:

【图论】Prim算法
一.介绍 Prim算法是一种用于解决最小生成树问题的贪心算法。最小生成树问题是指在一个连通无向图中找到一个生成树,使得树中所有边的权重之和最小。 Prim算法的基本思想是从一个起始顶点开始,逐步扩展生成树,直到覆盖所有顶点。具体步骤如下…...

第九十二回 在Flutter中解析JSON数据
文章目录 概念介绍解析方法convert库插件工具 示例代码经验总结 我们在上一章回中介绍了"对dio库进行封装"相关的内容,本章回中将介绍 如何在Flutter中解析JSON数据.闲话休提,让我们一起Talk Flutter吧。 概念介绍 我们在前面章回中介绍了通…...
银河麒麟安装mysql数据库(mariadb)-银河麒麟安装JDK-银河麒麟安装nginx(附安装包)
银河麒麟离线全套安装教程(手把手教程) 1.银河麒麟服务器系统安装mysql数据库(mariadb) 2.银河麒麟桌面系统安装mysql数据库(mariadb) 3.银河麒麟服务器系统安装JDK 4.银河麒麟桌面系统安装JDK 5.银河麒麟…...
文件上传
js绕过 打开网页尝试上传一句话木马,发现只能上传图片文件 审计源代码,发现使用一个checkfile函数js对文件类型进行了屏蔽 于是我们修改网页代码,去除返回值的检查函数 checkFile() 上传成功,使用蚁剑连接 连接成功 .htaccess绕…...
tinkerCAD案例:22. Backpack Zipper Pull 背包拉链头
tinkerCAD案例:21. Custom Stamp 定制印章 原文 tinkerCAD案例:22. Backpack Zipper Pull 背包拉链头 Lesson Overview: 课程概述: Now we’re going to make a zipper pull! 现在我们要做一个拉链头! Your backpack, howev…...
Unity 性能优化四:UI耗时函数、资源加载、卸载API
UI耗时函数 1.1 Canvas.SendWillRenderCanvases 这个函数是由于自身UI的更新,产生的耗时 1. 这里更新的是vertex 属性,比如 color、tangent、position、uv,修改recttransform的position、scale,rotation并不会导致顶点属性改变…...
【Linux】用户相关内容
如果命令ll 出现以上信息,UID为具体的数字,代表之前UID为502的用户被删除了。 更改目录或文件所属用户和所属组 在Linux中,创建一个文件时,该文件的拥有者都是创建该文件的用户。 更改所属用户 chown 用户名 文件名/目录名 更…...
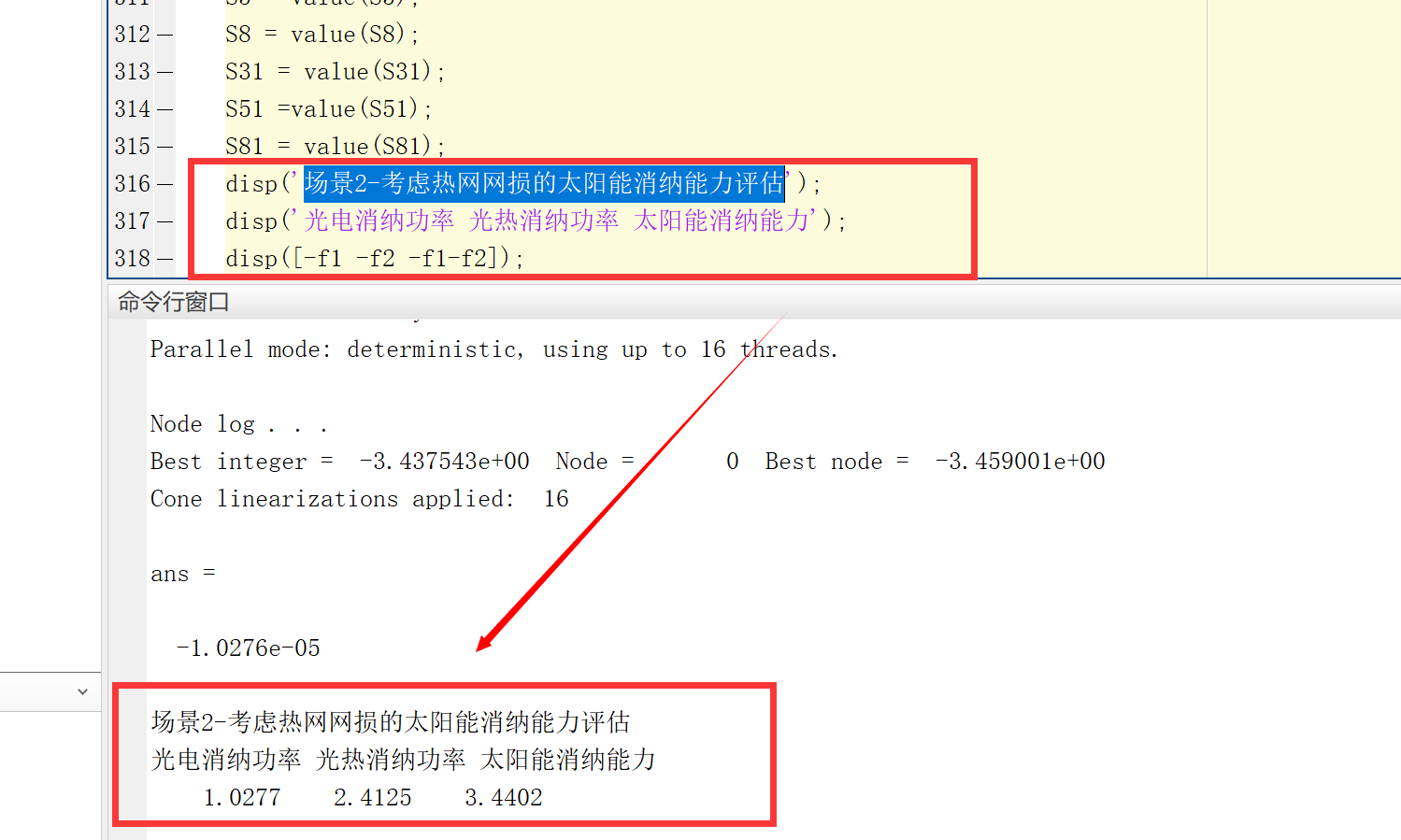
基于多场景的考虑虑热网网损的太阳能消纳能力评估研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

【动态规划part10】| 121.买卖股票的最佳时机、122.买卖股票的最佳时机II
目录 🎈LeetCode121. 买卖股票的最佳时机 🎈LeetCode122.买卖股票的最佳时机II 🎈LeetCode121. 买卖股票的最佳时机 链接:121.买卖股票的最佳时机 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定…...

java 页面html常用写法总结
(注意:本文章默认base html中已经引入bootstrap.min.css、style.css等css样式) input :输入标签 <#input required"必填" id"cycle" name"周期" underline"true" style"width:75%" itype&quo…...
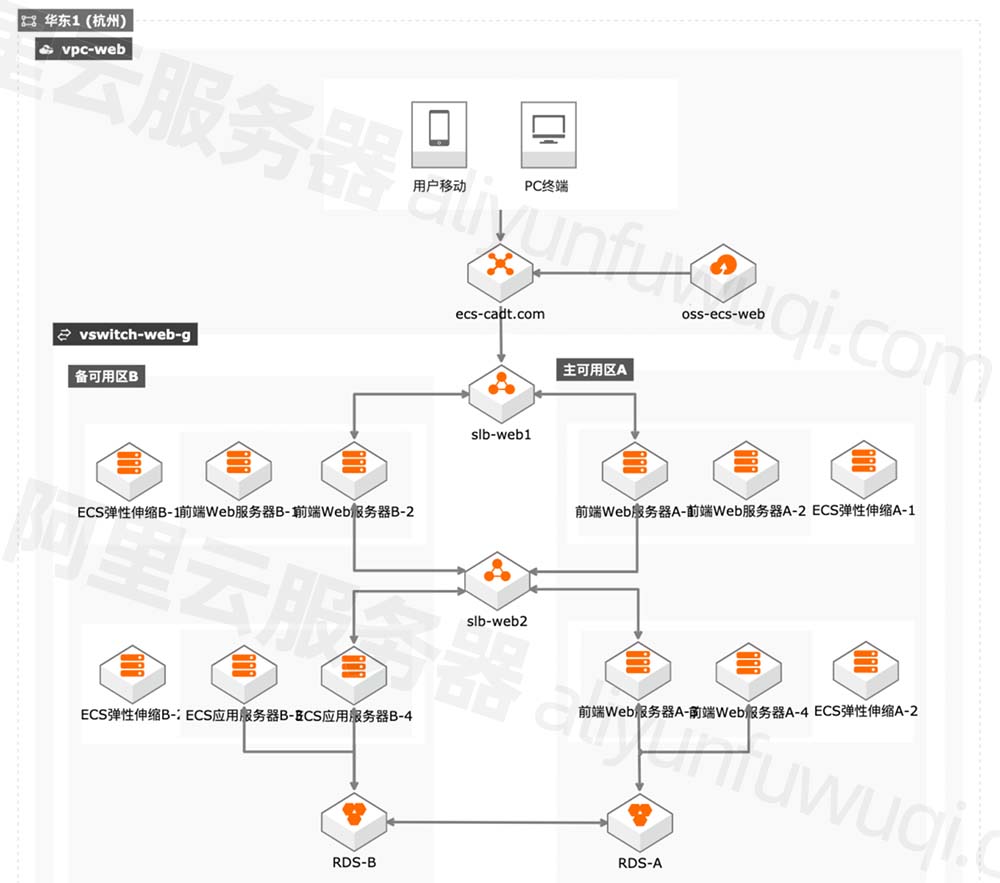
阿里云服务器全方位介绍_优势_使用_租用费用详解
阿里云服务器全方位介绍包括云服务器ECS优势、云服务器租用价格、云服务器使用场景及限制说明,阿里云服务器网分享云服务器ECS介绍、个人和企业免费试用、云服务器活动、云服务器ECS规格、优势、功能及应用场景详细你说明: 目录 什么是云服务器ECS&…...
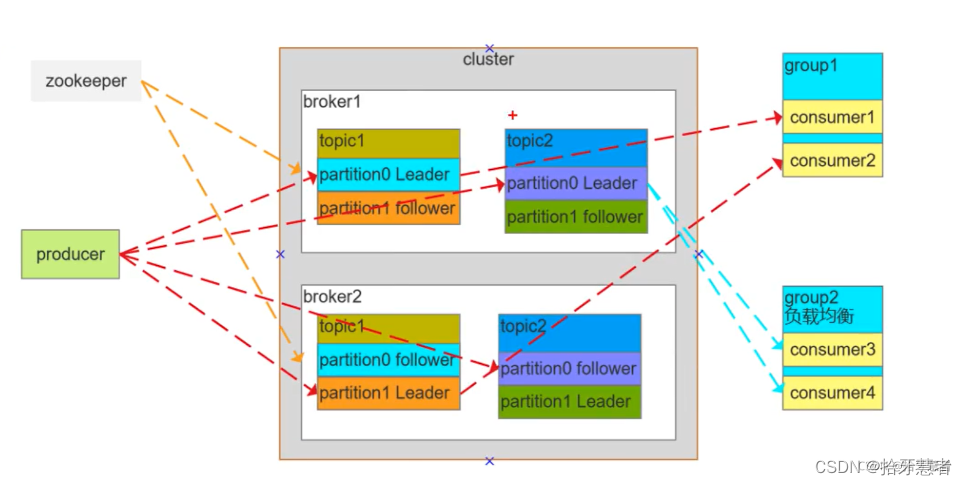
【Kafka】常用操作
1、基本概念 1. 消息: Kafka是一个分布式流处理平台,它通过消息进行数据的传输和存储。消息是Kafka中的基本单元,可以包含任意类型的数据。 2. 生产者(Producer): 生产者负责向Kafka主题发送消息。它将消息…...
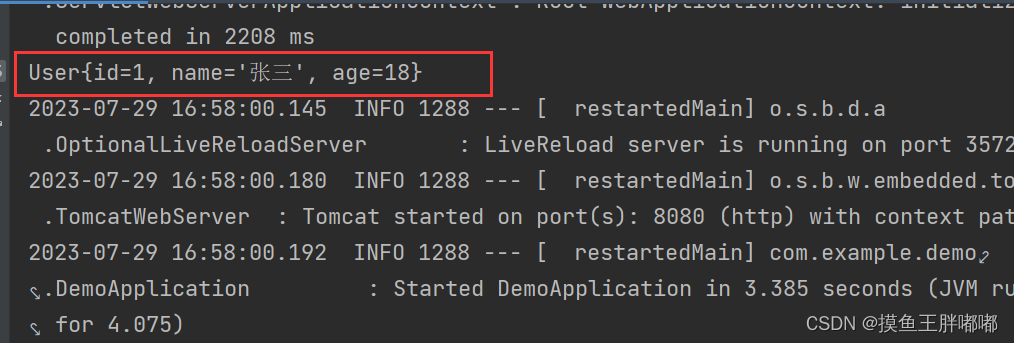
【Spring框架】SpringBoot配置文件
目录 配置文件作用application.properties中午乱码问题:配置文件里面的配置类型分类SpringBoot热部署properties基本语法properties配置文件的优缺点:yml配置文件说明yml基本语法配置对象properties VS yml 配置文件作用 整个项⽬中所有重要的数据都是在…...
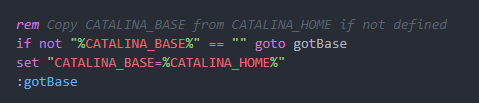
部署问题集合(十八)Windows环境下使用两个Tomcat
下载Tomcat Tomcat镜像下载地址:https://mirrors.cnnic.cn/apache/tomcat/进入如下地址:zip的是压缩版,exe是安装版 修改第二个Tomcat配置文件 第一步:编辑conf/server.xml文件,修改三个端口,有些版本改…...

数据结构问答8
查找 1. 一些基本概念 关键字:能唯一标识该元素 查找:给定值k,在含n个元素的表中找出关键字==k的元素。找到返回其位置信息,否则返回-1。 动、静态查找表:查找同时对表进行修改(插入、删除等),相应的表为动态,否则为静态。 内、外查找:整个查找过程在内存中进行…...

行为型设计模式之观察者模式【设计模式系列】
系列文章目录 C技能系列 Linux通信架构系列 C高性能优化编程系列 深入理解软件架构设计系列 高级C并发线程编程 设计模式系列 期待你的关注哦!!! 现在的一切都是为将来的梦想编织翅膀,让梦想在现实中展翅高飞。 Now everythi…...
)
vue2企业级项目(四)
vue2企业级项目(四) 路由设计,过场动画设计 1、router 项目下载依赖 npm install --save vue-router3.5.3src目录下创建router/index.js import Vue from "vue"; import Router from "vue-router";Vue.use(Router);con…...

(树) 剑指 Offer 26. 树的子结构 ——【Leetcode每日一题】
❓剑指 Offer 26. 树的子结构 难度:中等 输入两棵二叉树 A 和 B,判断 B 是不是 A 的子结构。(约定空树不是任意一个树的子结构) B 是 A 的子结构, 即 A 中有出现和B相同的结构和节点值。 例如: 给定的树 A: 3/ \4 5/ \1 2给定的树 B&…...
Linuxcnc-ethercat从入门到放弃(1)、环境搭建
项目开源网站 LinuxCNChttps://www.linuxcnc.org/当前release版本2.8.4 Downloads (linuxcnc.org)https://www.linuxcnc.org/downloads/可以直接下载安装好linuxcnc的实时debian系统,直接刻盘安装就可以了 安装IgH主站,网上有很多教程可供参考 git clo…...

14.Netty源码之模拟简单的HTTP服务器
highlight: arduino-light 简单的 HTTP 服务器 HTTP 服务器是我们平时最常用的工具之一。同传统 Web 容器 Tomcat、Jetty 一样,Netty 也可以方便地开发一个 HTTP 服务器。我从一个简单的 HTTP 服务器开始,通过程序示例为你展现 Netty 程序如何配置启动&a…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...
