R数据分析:孟德尔随机化中介的原理和实操二
delta方法
上面的流程跑通之后,对于中介分析,我们需要报告间接效应的估计值和置信区间,还有中介比例的估计值和置信区间,类似下面的这样:
但是其实我们是光跑孟德尔是得不到上面的需要的值的(比如间接效应的标准误,中介比例的标准误),此时需要借助的方法之一叫做delta method。
As individual level data is not available in summary data MR, bootstrapping cannot be used to estimate the confidence intervals for the indirect effect or proportion mediated, but the delta method can be used to approximate these confidence intervals if samples are independent
delta method可以帮助我们得到ab相乘的标准误,从而算出中介效应的置信区间。
也就是说我们知道了A,B路径的点估计和标准误,根据上面的公式就可以得到间接效应的置信区间,在R中实现起来也容易的,使用RMediation包,这个包作者有开发shiny应用,输入A,B的估计值和标准误就可以得到间接效应的估计值和标准误和置信区间了(下图圈内):
bootstrap方法
bootstrap方法也可以用来帮助我们计算中介效应和中介比例的置信区间:
Bootstrapping is a technique used in inferential statistics that work on building random samples of single datasets again and again. Bootstrapping allows calculating measures such as mean, median, mode, confidence intervals, etc. of the sampling.
bootstrap基本思路是对原来的分析数据进行有放回的随机抽样形成抽样数据集,bootstrap1000次就会形成1000个抽样数据集,每个抽样数据集都可以算我们需要的统计量,这样统计量的分布就出来了,也就有了置信区间。
bootstrap对象生成后计算中介效应和中介比例部分代码见下:
通过bootstrap形成比如1000个统计量的分布后,取0.025,0.975百分位就是95置信区间.
此处我们再补一个bootstrap过程的例子,在做bootstrap的时候我们需要用到boot函数,主要参数就3个:
其中最重要的就是我们需要计算的统计量statistic,这个是以函数的形式给出的,并且该函数接受不少于2个参数,一个是数据,另一个是抽样的indices。
为了对比我先将跑的孟德尔随机化的结果贴出来:
结果中有正常跑出来的b和对应的se,我通过bootstrap再将5个se跑出来,作为对比演示,代码如下:
mr_function <- function(data, indices) {d <- dat[indices,] jieguo <- mr(d) return(jieguo %>% pull(b))
}
reps_mr <- boot(data=dat, statistic=mr_function, R=1000)上面的代码中mr_function是我要喂给boot函数的statistic参数,在mr_function已经申明了我返回的值,也就是我要bootstrap的统计量是MR结果的b,所以运行完了会出来5个b的bootstrap的SE。
因为计算时间太长,上面就只设置了抽1000个数据集,数据不算很密,看看情况:
可以看到5种方法的系数的bootstrapt标准误都出来了,但是t3也就是IVW方法的标准误通过bootstrap是最接近原来值的,这应该也是为什么报告中介都是依照IVW的系数的原因之一。
上面演示的目的只是bootstrap的做法过程,实际我们需要改动mr_function中的return为我们需要的统计量,也就是中介效应和中介效应占比。
Propagation of error
再计算中介效应和中介比例的置信区间时也可以用误差传染法,比如下面这篇文献:
这个方法比较好理解,顺带也写个例子给大家介绍一下
Propagation of error refers to the methods used to determine how the uncertainty in a
calculated result is related to the uncertainties in the individual measure
误差传染法的计算积的标准差的过程如下:
完全是初中的多项式乘法,中间涉及到把较小的项删掉,应该看懂没问题,这儿就不写解释了。商的标准差计算如下:
中间过程涉及到高中的极限,总体也不难,上面的方法就是“误差传染法”Propagation of error。掌握积和商的标准差的算法后,我们在用Two-step MR得到a和b之后就可以得到得到中介效应ab的置信区间,相应地用商的标准差算法可以算出中介占比的置信区间。
上面介绍的方法帮助我们计算出来标准误后通过正态近似后和界值对比即可得到相应的p值,比如中介效应分布画出来后和界值0对比,分布曲线下横轴和0轴曲线下面积即为p值。
整个的孟德尔随机化中介就给大家分享完了。
相关文章:

R数据分析:孟德尔随机化中介的原理和实操二
delta方法 上面的流程跑通之后,对于中介分析,我们需要报告间接效应的估计值和置信区间,还有中介比例的估计值和置信区间,类似下面的这样: 但是其实我们是光跑孟德尔是得不到上面的需要的值的(比如间接效应…...
:三问(如何对字符串字母去重后按字母顺序排列字符串?如何识别哪些字符串中包含数字?如何将分隔数据转换为多值IN列表?))
【SQL开发实战技巧】系列(十二):三问(如何对字符串字母去重后按字母顺序排列字符串?如何识别哪些字符串中包含数字?如何将分隔数据转换为多值IN列表?)
系列文章目录 【SQL开发实战技巧】系列(一):关于SQL不得不说的那些事 【SQL开发实战技巧】系列(二):简单单表查询 【SQL开发实战技巧】系列(三):SQL排序的那些事 【SQL开发实战技巧…...

数据库模式(schema)是什么?
在数据库的术语中,模式(schema)是一个逻辑概念,用于组织数据库中的对象。模式中的对象通常包括表、索引、数据类型、序列、视图、存储过程、主键、外键等等。 模式可以为数据库对象提供逻辑隔离功能,不用应用程序可以…...
出现failed to load steamui.dll如何解决?好的修复方法推荐
当你电脑突然出现failed to load steamui.dll的时候,你是否一脸懵逼?根本不知道发生啥时候,突然就会这样报错,其实造成这个原因,主要是因为问题出在steam上,我们还是有很多种方法可以解决的,今天…...

js 原生事件触发
var event nullevent new Event(input);document.querySelectorAll("input[placeholder点击网址 选择远端数据字典网址]")[0].dispatchEvent(event)...

Nacos安装配置(二)
目录 一、概述 二、Nacos 安装 A)Debian11 1)软件环境 2)下载源码或者安装包 3)mysql配置 4)启动服务器 B) Debian11 1) 安装JDK 2) 安装Maven 3) 安装Nacos2 4) 修改访问参数(/conf/applicati…...
【Linux基础知识】
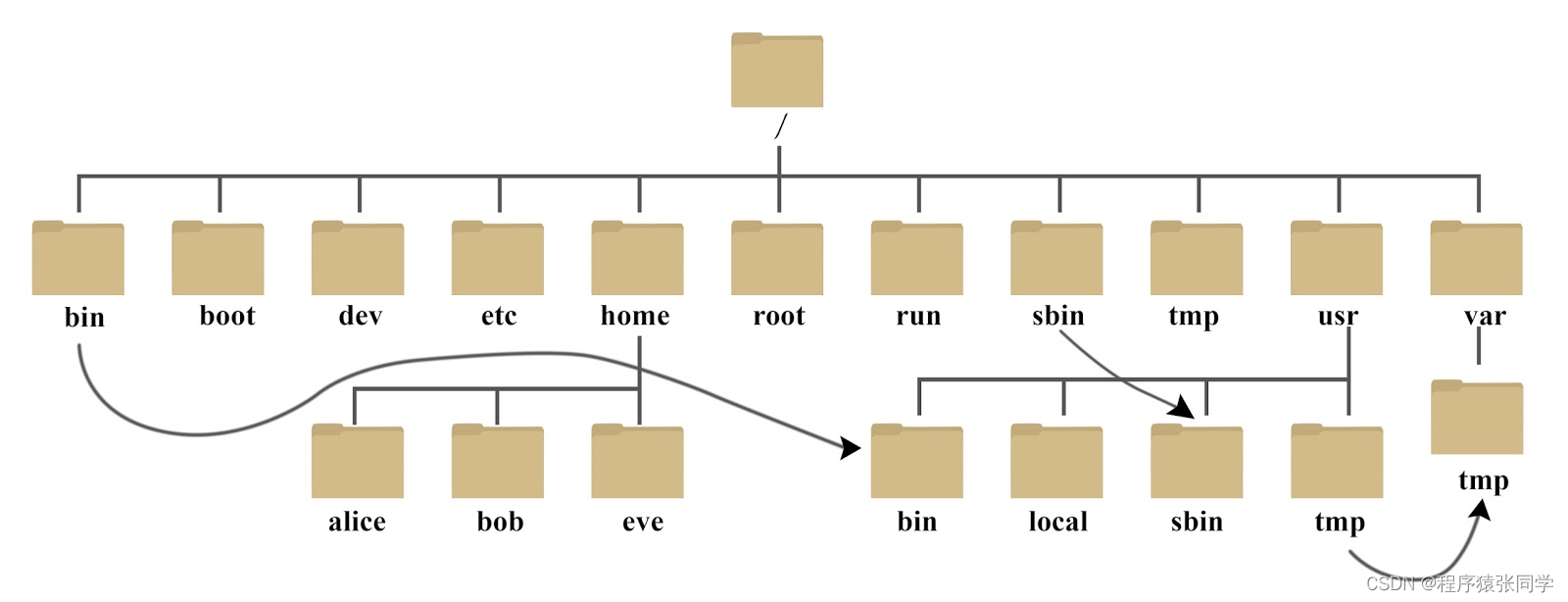
Linux基础知识 Linux基础知识 系统目录结构 /bin: 命令和应用程序。 /boot: 这里存放的是启动 Linux 时使用的一些核心文件,包括一些连接文件以及镜像文件。 /dev : dev 是 Device(设备) 的缩写, 该目录下存放的是 Linux 的外…...

【王道数据结构】第七章| 查找 | 树
目录 一、查找 1、查找概念 2、顺序查找 3、折半查找 4、分块查找 二、树 1、B树 2、B树的基本操作 3、B树 4、散列查找及其性能分析 5、散列查找及性能分析 一、查找 1、查找概念 查找:在数据集合中寻找满足某种条件的数据元素的过程称为查找。查找…...

VBA提高篇_19 可选参数Optional_ IsMissing _MSgbox
文章目录1. 可选参数Optional2.IsMissing判断参数是否提供,只能判断变体类型3. 使用 : 可以按参数名传递参数 a:1,c:34.Msgbox 常用参数5.VBA颜色常量表1. 可选参数Optional Optional 代表本参数是可选项 False ; 代表参数若不指定,则默认为False Function mySumProduct(r As R…...

【子网划分】求子网网络前缀、子网地址、每个子网可以分配给主机使用的最小地址和最大地址
1、某单位分配到一个地址块152.7.77.0/24,现在需要进一步划分为4个一样大的子网。(10分) 问题: (1) 每个子网的网络前缀有多长? (2) 每一个子网中有多少个地址? (3) 每一个子网的网络地址是什么?…...
网络协议安全
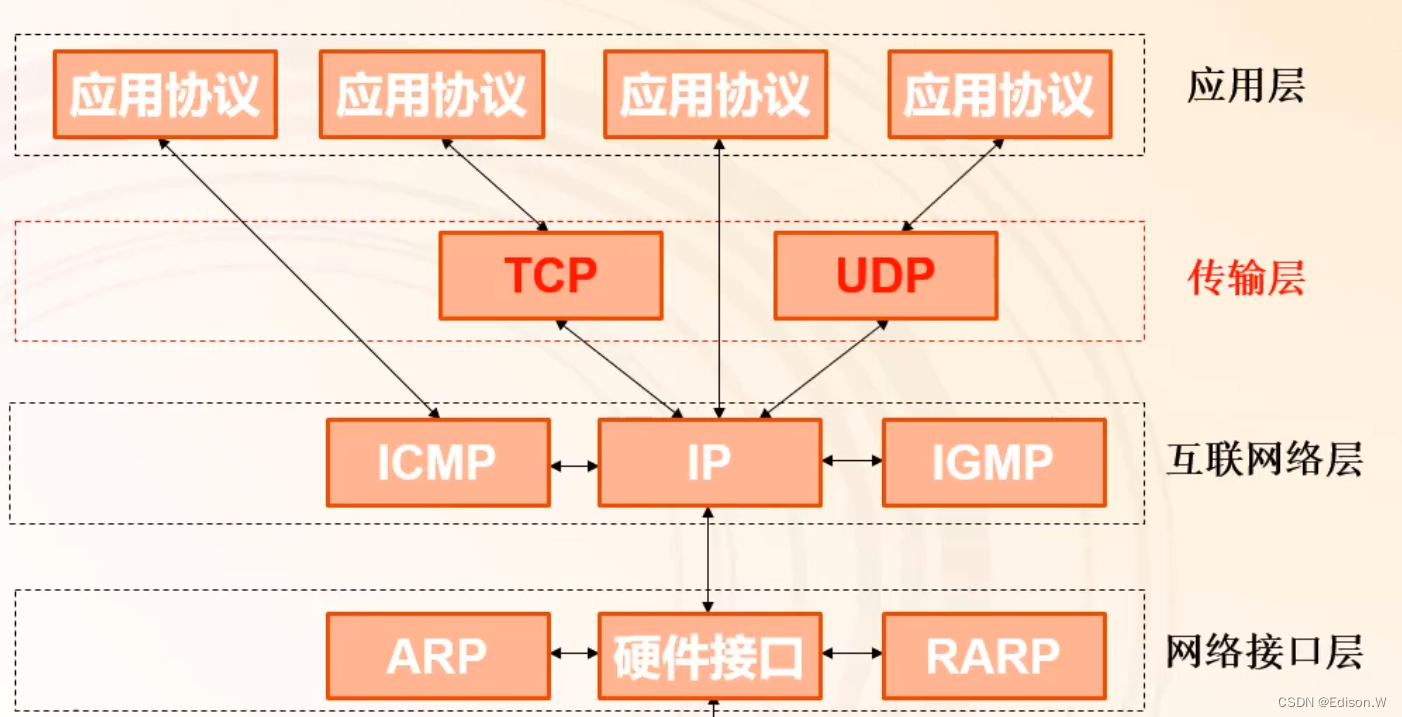
网络协议安全网络协议ISO/OSI七层模型OSI模型与TCP/IP模型网络接口与互联网层安全传输层与应用层安全传输层协议-TCP协议传输层协议-UDP协议网络协议 ISO/OSI七层模型 物理层 作用:定义物理链路的前期、机械、通信规程、功能要求等将比特流庄换成电压典型物理层设备…...

ImportError: /lib64/libm.so.6: version `GLIBC_2.23‘ not found问题解决方法
1.环境:Centos7,GCC version 9.1.0,python3.7,TensorFlow1.14.0.因为/usr/lib64/libstdc.so.6: version CXXABI_1.3.8 not found问题,我将GCC版本升级到了9.1.0,但是运行TensorFlow的时候出现了ImportError…...

盂县基本情况
寒假的活动报告,万物皆可CSDN,贴一下吧 盂县隶属于阳泉市,阳泉市是李彦宏和刘慈欣的家乡,阳泉市内有百度云计算中心 基本情况 盂县,隶属山西省阳泉市,地处山西省东部、太行山西麓,东与河北省平…...
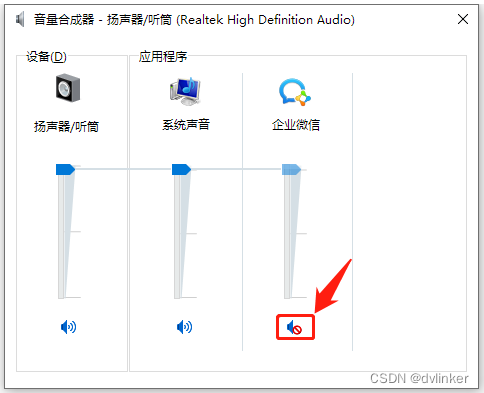
VC++打开或关闭目标进程的声音(扬声器)(附源码)
VC常用功能开发汇总(专栏文章列表,欢迎订阅,持续更新...)https://blog.csdn.net/chenlycly/article/details/124272585C软件异常排查从入门到精通系列教程(专栏文章列表,欢迎订阅,持续更新...&a…...

LeetCode 每日一题 2023/1/23-2023/1/29
记录了初步解题思路 以及本地实现代码;并不一定为最优 也希望大家能一起探讨 一起进步 目录1/23 2303. 计算应缴税款总额1/24 1828. 统计一个圆中点的数目1/25 1632. 矩阵转换后的秩1/26 1663. 具有给定数值的最小字符串1/27 2309. 兼具大小写的最好英文字母1/28 16…...

Hadoop组件Yarn常见命令
Hadoop组件Yarn常见命令 一、概述 当我们不能使用ResourceManager Web UI时,就需要使用Yarn命令来处理问题。因此,我们需要了解如何使用yarn命令监控YARN集群。 Hadoop的yarn命令具有广泛的使用范围: 它可以帮助我们管理大量的MR、Spark、Flink任务。例如获取和杀死正在运…...
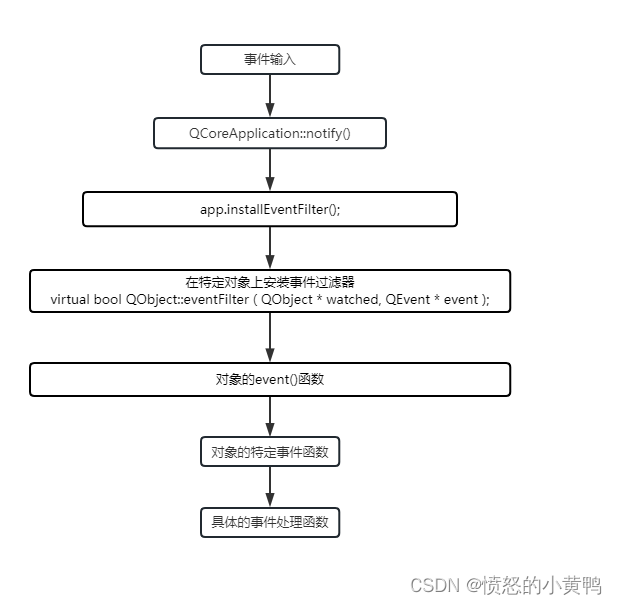
QT之事件系统
QT之事件系统1. 概述2. 事件的传递3. 事件类型4. 事件处理与事件过滤5. 自定义事件5.1 Demo6. 发送事件7. 参考1. 概述 在QT中,事件均派生自QEvent抽象类,事件可以由任何派生自QObject的子类实例接收和处理。它们与widget关联性极强。 2. 事件的传递 …...

Python中__init__.py文件深入理解
Python中文件__init__.py深入理解1. 简介1.1 模块(Module)和包(Package)的概念1.2 __init__.py文件简介2. __init__.py内容写法2.1 __init__.py文件内容2.2 __init__.py内容解释1. 简介 1.1 模块(Module)和…...
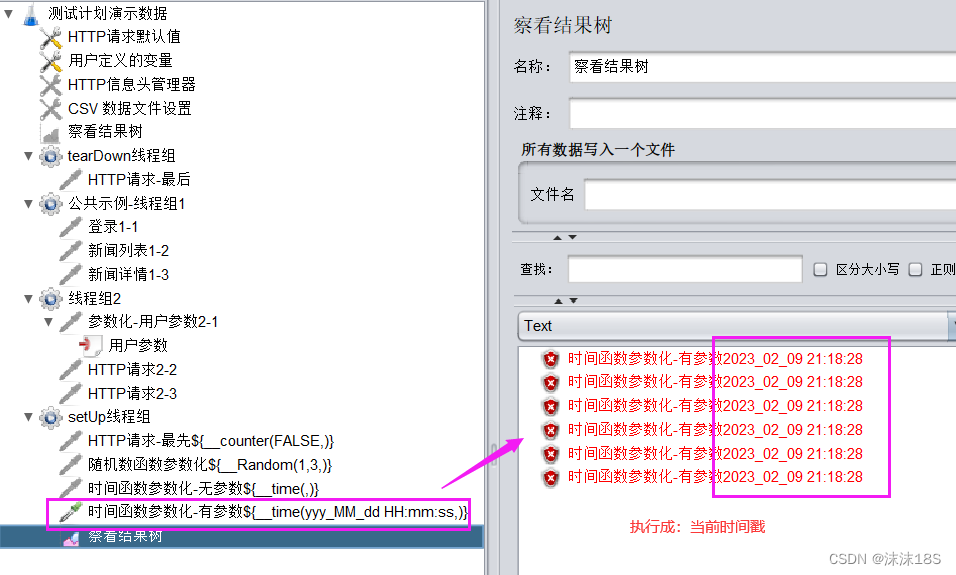
Jmeter之实现参数化的不同方式详解
参数化简介 定义:动态的获取、设置或生成数据,是一种由程序驱动代替人工驱动的数据设计方案,提高脚本的编写效率以及编写质量 适用场景:当提交的数据量较大时,每次修改太麻烦,可以使用参数化 本文介绍实现…...
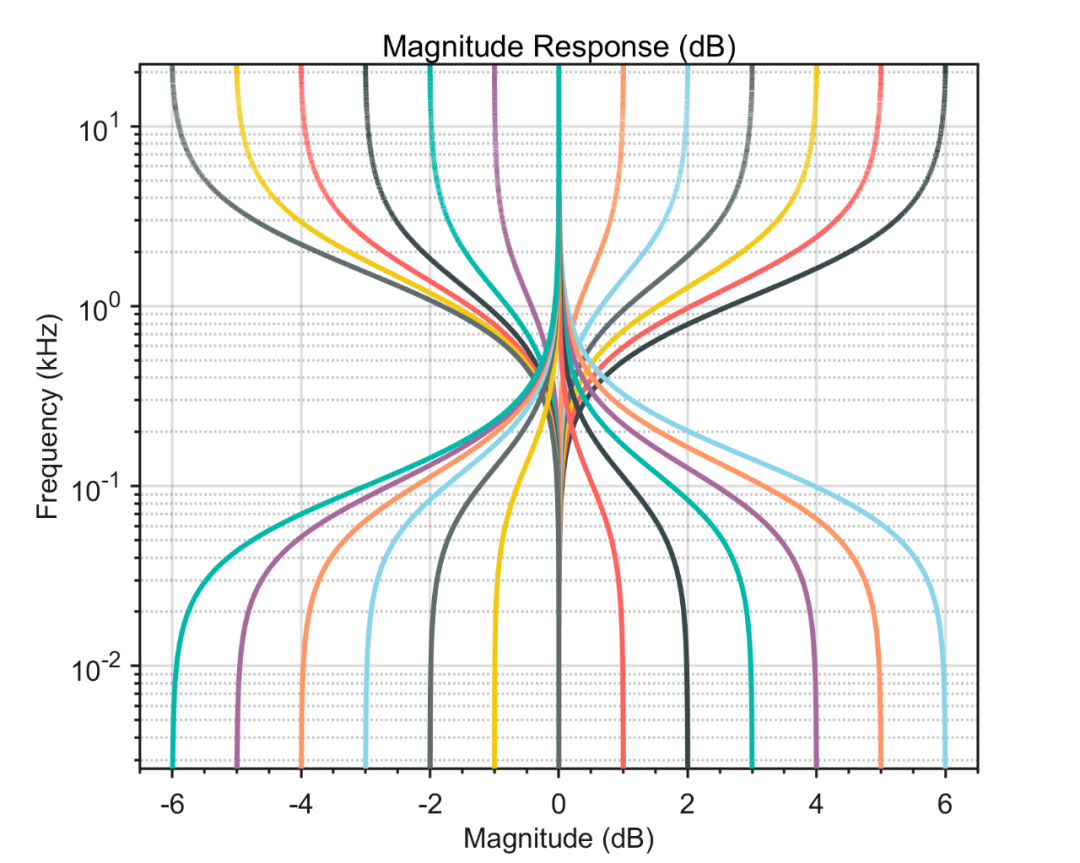
Matlab论文插图绘制模板第76期—半对数刻度折线图(Semilogx和Semilogy)
在之前的文章中,分享了Matlab双对数刻度折线图的绘制模板: 进一步,再来分享一下半对数刻度折线图的绘制模板。 先来看一下成品效果: 特别提示:Matlab论文插图绘制模板系列,旨在降低大家使用Matlab进行科研…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...

AT模式下的全局锁冲突如何解决?
一、全局锁冲突解决方案 1. 业务层重试机制(推荐方案) Service public class OrderService {GlobalTransactionalRetryable(maxAttempts 3, backoff Backoff(delay 100))public void createOrder(OrderDTO order) {// 库存扣减(自动加全…...

02-性能方案设计
需求分析与测试设计 根据具体的性能测试需求,确定测试类型,以及压测的模块(web/mysql/redis/系统整体)前期要与相关人员充分沟通,初步确定压测方案及具体的性能指标QA完成性能测试设计后,需产出测试方案文档发送邮件到项目组&…...
