代码随想录算法训练营day45
文章目录
- Day45
- 爬楼梯
- 题目
- 思路
- 代码
- 零钱兑换
- 题目
- 思路
- 代码
- 完全平方数
- 题目
- 思路
- 代码
Day45
爬楼梯
70. 爬楼梯 - 力扣(LeetCode)
题目
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
示例 1: 输入: 2 输出: 2 解释: 有两种方法可以爬到楼顶。
- 1 阶 + 1 阶
- 2 阶
示例 2: 输入: 3 输出: 3 解释: 有三种方法可以爬到楼顶。
- 1 阶 + 1 阶 + 1 阶
- 1 阶 + 2 阶
- 2 阶 + 1 阶
思路
动规五部曲分析如下:
- 确定dp数组以及下标的含义
dp[i]:爬到有i个台阶的楼顶,有dp[i]种方法。
- 确定递推公式
在动态规划:494.目标和 (opens new window)、 动态规划:518.零钱兑换II (opens new window)、动态规划:377. 组合总和 Ⅳ (opens new window)中我们都讲过了,求装满背包有几种方法,递推公式一般都是dp[i] += dp[i - nums[j]];
本题呢,dp[i]有几种来源,dp[i - 1],dp[i - 2],dp[i - 3] 等等,即:dp[i - j]
那么递推公式为:dp[i] += dp[i - j]
- dp数组如何初始化
既然递归公式是 dp[i] += dp[i - j],那么dp[0] 一定为1,dp[0]是递归中一切数值的基础所在,如果dp[0]是0的话,其他数值都是0了。
下标非0的dp[i]初始化为0,因为dp[i]是靠dp[i-j]累计上来的,dp[i]本身为0这样才不会影响结果
- 确定遍历顺序
这是背包里求排列问题,即:1、2 步 和 2、1 步都是上三个台阶,但是这两种方法不一样!
所以需将target放在外循环,将nums放在内循环。
每一步可以走多次,这是完全背包,内循环需要从前向后遍历。
- 举例来推导dp数组
介于本题和动态规划:377. 组合总和 Ⅳ (opens new window)几乎是一样的,这里我就不再重复举例了。
代码
class Solution {public int climbStairs(int n) {int dp[] = new int[n + 1];int step[] = new int[]{1,2};dp[0] = 1;for(int i = 0; i < n + 1; i++){for(int j = 0; j < step.length; j++){if(i >= step[j]){dp[i] += dp[i - step[j]];}}}return dp[n];}
}
零钱兑换
322. 零钱兑换 - 力扣(LeetCode)
题目
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
你可以认为每种硬币的数量是无限的。
示例 1:
- 输入:coins = [1, 2, 5], amount = 11
- 输出:3
- 解释:11 = 5 + 5 + 1
示例 2:
- 输入:coins = [2], amount = 3
- 输出:-1
示例 3:
- 输入:coins = [1], amount = 0
- 输出:0
示例 4:
- 输入:coins = [1], amount = 1
- 输出:1
示例 5:
- 输入:coins = [1], amount = 2
- 输出:2
提示:
- 1 <= coins.length <= 12
- 1 <= coins[i] <= 2^31 - 1
- 0 <= amount <= 10^4
思路
- 确定dp数组以及下标的含义
dp[j]: 凑出 j 元最少需要 dp[j] 枚硬币
- 确定递推公式
凑足总额为j - coins[i]的最少个数为dp[j - coins[i]],那么只需要加上一个钱币coins[i]即dp[j - coins[i]] + 1就是dp[j](考虑coins[i])
所以dp[j] 要取所有 dp[j - coins[i]] + 1 中最小的。
递推公式:dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
- dp数组如何初始化
首先凑足总金额为0所需钱币的个数一定是0,那么dp[0] = 0;
其他下标对应的数值呢?
考虑到递推公式的特性,dp[j]必须初始化为一个最大的数,否则就会在min(dp[j - coins[i]] + 1, dp[j])比较的过程中被初始值覆盖。
所以下标非0的元素都是应该是最大值。
- 确定遍历顺序
本题求钱币最小个数,那么钱币有顺序和没有顺序都可以,都不影响钱币的最小个数。
所以本题并不强调集合是组合还是排列。
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
在动态规划专题我们讲过了求组合数是动态规划:518.零钱兑换II (opens new window),求排列数是动态规划:377. 组合总和 Ⅳ (opens new window)。
所以本题的两个for循环的关系是:外层for循环遍历物品,内层for遍历背包或者外层for遍历背包,内层for循环遍历物品都是可以的!
那么我采用coins放在外循环,target在内循环的方式。
本题钱币数量可以无限使用,那么是完全背包。所以遍历的内循环是正序
- 举例推导dp数组
以输入:coins = [1, 2, 5], amount = 5为例
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-nOwSZb9p-1690615913100)(https://code-thinking-1253855093.file.myqcloud.com/pics/20210201111833906.jpg “322.零钱兑换”)]
代码
class Solution {public int coinChange(int[] coins, int amount) {int dp[] = new int[amount + 1];Arrays.fill(dp, Integer.MAX_VALUE);dp[0] = 0;for(int i = 0; i < amount + 1; i++){for(int j = 0; j < coins.length; j++){if(i >= coins[j] && dp[i - coins[j]] != Integer.MAX_VALUE){dp[i] = Math.min(dp[i], dp[i - coins[j]] + 1);}}}return dp[amount] == Integer.MAX_VALUE ? -1 : dp[amount];}
}
完全平方数
279. 完全平方数 - 力扣(LeetCode)
题目
给定正整数 n,找到若干个完全平方数(比如 1, 4, 9, 16, …)使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。
给你一个整数 n ,返回和为 n 的完全平方数的 最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
- 输入:n = 12
- 输出:3
- 解释:12 = 4 + 4 + 4
示例 2:
- 输入:n = 13
- 输出:2
- 解释:13 = 4 + 9
提示:
- 1 <= n <= 10^4
思路
可能刚看这种题感觉没啥思路,又平方和的,又最小数的。
我来把题目翻译一下:完全平方数就是物品(可以无限件使用),凑个正整数n就是背包,问凑满这个背包最少有多少物品?
感受出来了没,这么浓厚的完全背包氛围
- 确定dp数组(dp table)以及下标的含义
dp[j]:和为j的完全平方数的最少数量为dp[j]
- 确定递推公式
dp[j] 可以由dp[j - i * i]推出, dp[j - i * i] + 1 便可以凑成dp[j]。
此时我们要选择最小的dp[j],所以递推公式:dp[j] = min(dp[j - i * i] + 1, dp[j]);
- dp数组如何初始化
dp[0]表示 和为0的完全平方数的最小数量,那么dp[0]一定是0。
有同学问题,那0 * 0 也算是一种啊,为啥dp[0] 就是 0呢?
看题目描述,找到若干个完全平方数(比如 1, 4, 9, 16, …),题目描述中可没说要从0开始,dp[0]=0完全是为了递推公式。
非0下标的dp[j]应该是多少呢?
从递归公式dp[j] = min(dp[j - i * i] + 1, dp[j]);中可以看出每次dp[j]都要选最小的,所以非0下标的dp[j]一定要初始为最大值,这样dp[j]在递推的时候才不会被初始值覆盖。
- 确定遍历顺序
我们知道这是完全背包,
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
在动态规划:322. 零钱兑换 (opens new window)中我们就深入探讨了这个问题,本题也是一样的,是求最小数!
所以本题外层for遍历背包,内层for遍历物品,还是外层for遍历物品,内层for遍历背包,都是可以的!
- 举例推导dp数组
已输入n为5例,dp状态图如下:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-IoGWI7QK-1690615913101)(https://code-thinking-1253855093.file.myqcloud.com/pics/20210202112617341.jpg “279.完全平方数”)]
代码
class Solution {public int numSquares(int n) {int dp[] = new int[n + 1];Arrays.fill(dp, Integer.MAX_VALUE);dp[0] = 0;for(int i = 1; i < n + 1; i++){for(int j = 1; j * j <= i; j++){dp[i] = Math.min(dp[i], dp[i - j * j] + 1);}}return dp[n];}
}
相关文章:

代码随想录算法训练营day45
文章目录 Day45爬楼梯题目思路代码 零钱兑换题目思路代码 完全平方数题目思路代码 Day45 爬楼梯 70. 爬楼梯 - 力扣(LeetCode) 题目 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢…...
机器学习深度学习——softmax回归(上)
👨🎓作者简介:一位即将上大四,正专攻机器学习的保研er 🌌上期文章:机器学习&&深度学习——线性回归的简洁实现 📚订阅专栏:机器学习&&深度学习 希望文章对你们有所…...

基于express调用chatgpt文字流输出和有道智云语音合成
express是基于node.js的一个web框架,可以更加简洁的去创建一个后台服务,由于项目的需要,引入和typescript,经过几天的努力实现了chatgpt文字流输出有道智云语音合成的结合(略有遗憾),下面我记载…...
(学习笔记-内存管理)内存分段、分页、管理与布局
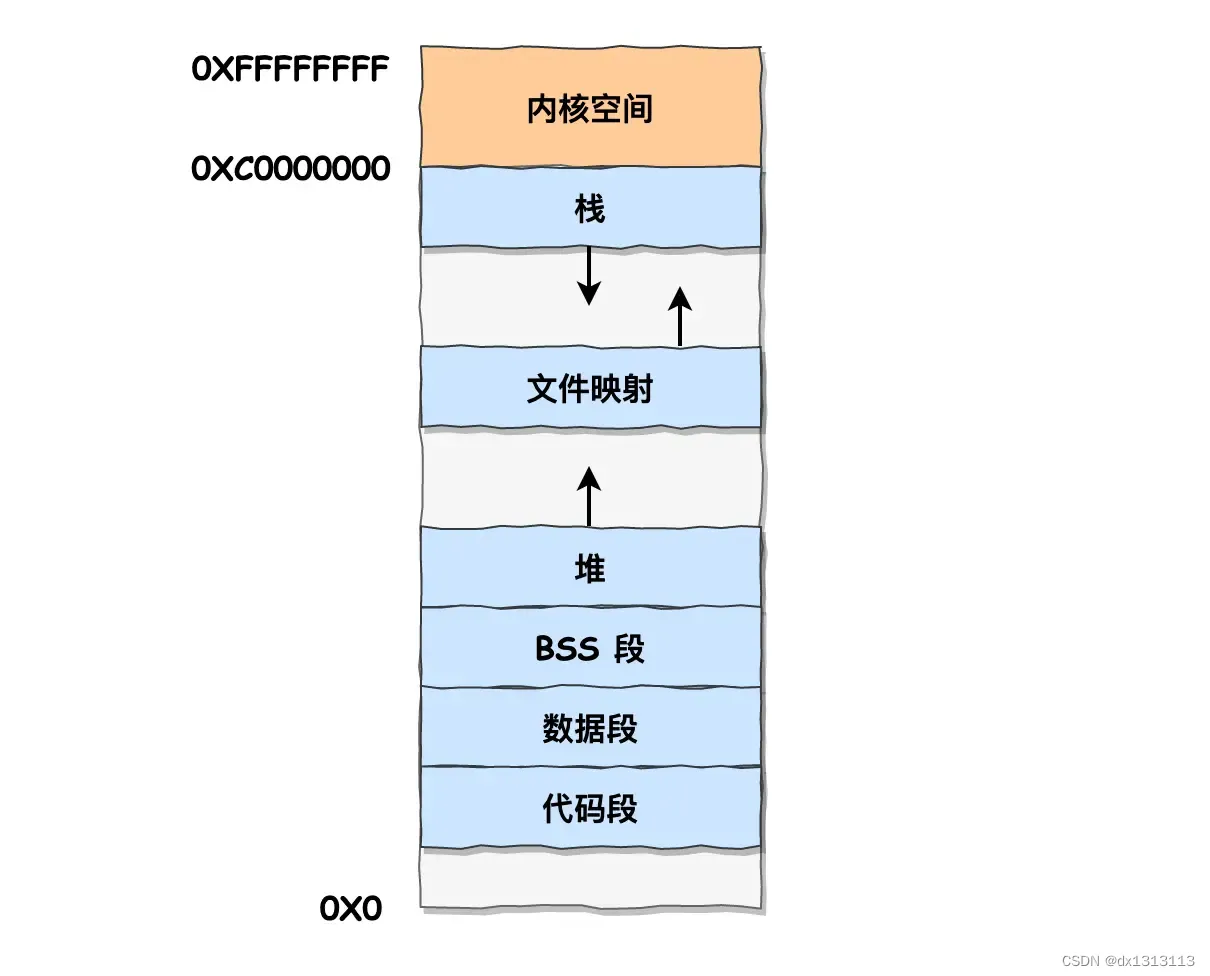
内存分段 程序是由若干个逻辑分段组成的,比如可由代码分段、数据分段、栈段、堆段组成。不同的段是有不同的属性的,所以就用分段的形式把这些分段分离出来。 分段机制下,虚拟地址和物理地址是如何映射的? 分段机制下的虚拟地址由…...
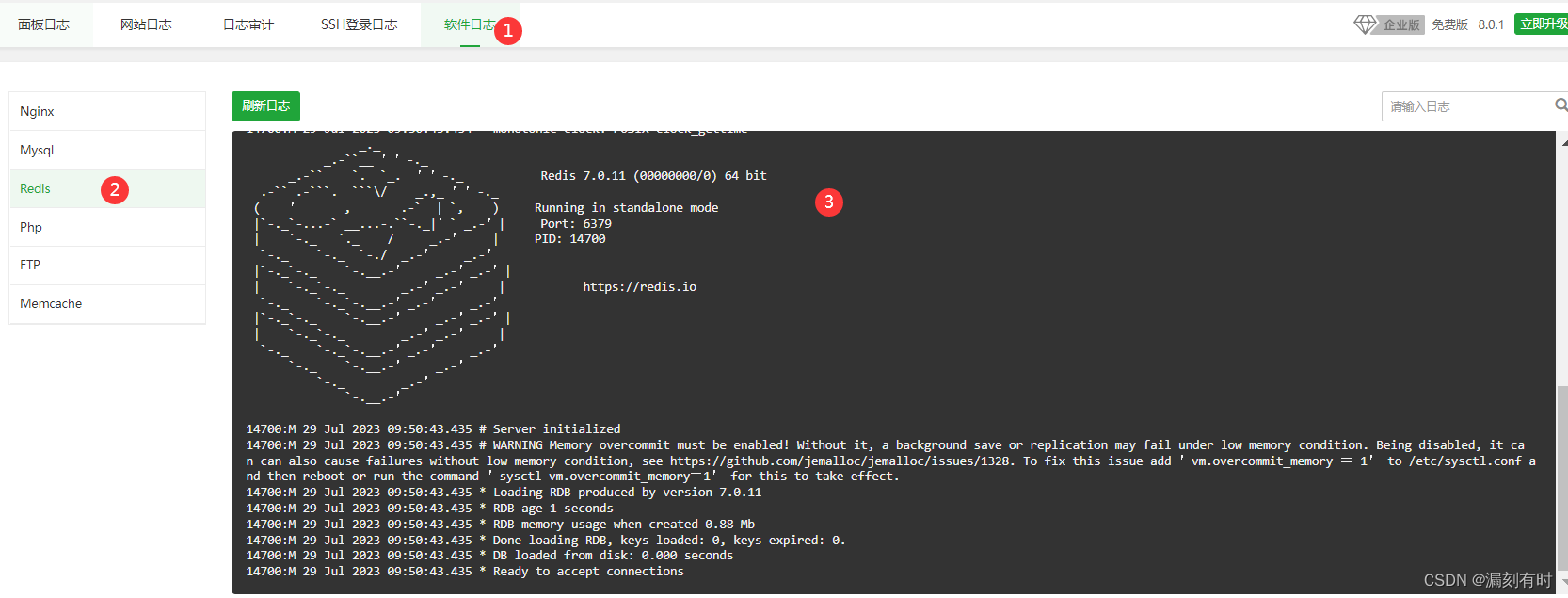
PHP使用Redis实战实录1:宝塔环境搭建、6379端口配置、Redis服务启动失败解决方案
宝塔环境搭建、6379端口配置、Redis服务启动失败解决方案 前言一、Redis安装部署1.安装Redis2.php安装Redis扩展3.启动Redis 二、避坑指南1.6379端口配置2.Redis服务启动(1)Redis服务启动失败(2)Redis启动日志排查(3&a…...
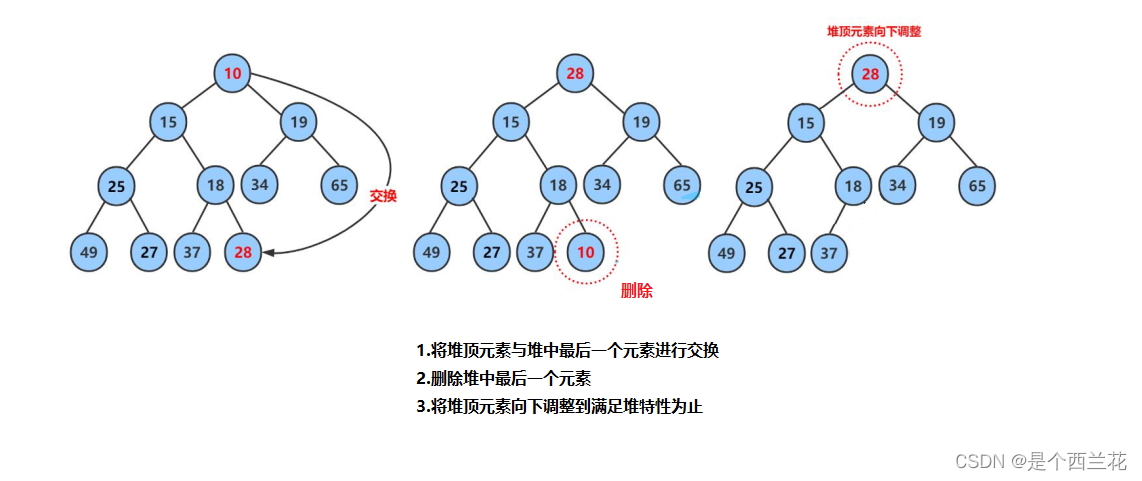
【数据结构】这堆是什么
目录 1.二叉树的顺序结构 2.堆的概念及结构 3.堆的实现 3.1 向上调整算法与向下调整算法 3.2 堆的创建 3.3 建堆的空间复杂度 3.4 堆的插入 3.5 堆的删除 3.6 堆的代码的实现 4.堆的应用 4.1 堆排序 4.2 TOP-K问题 首先,堆是一种数据结构,一种特…...
FFmpeg 音视频开发工具
目录 FFmpeg 下载与安装 ffmpeg 使用快速入门 ffplay 使用快速入门 FFmpeg 全套下载与安装 1、FFmpeg 是处理音频、视频、字幕和相关元数据等多媒体内容的库和工具的集合。一个完整的跨平台解决方案,用于录制、转换和流式传输音频和视频。 官网:http…...

Go 语言 select 都能做什么?
原文链接: Go 语言 select 都能做什么? 在 Go 语言中,select 是一个关键字,用于监听和 channel 有关的 IO 操作。 通过 select 语句,我们可以同时监听多个 channel,并在其中任意一个 channel 就绪时进行相…...
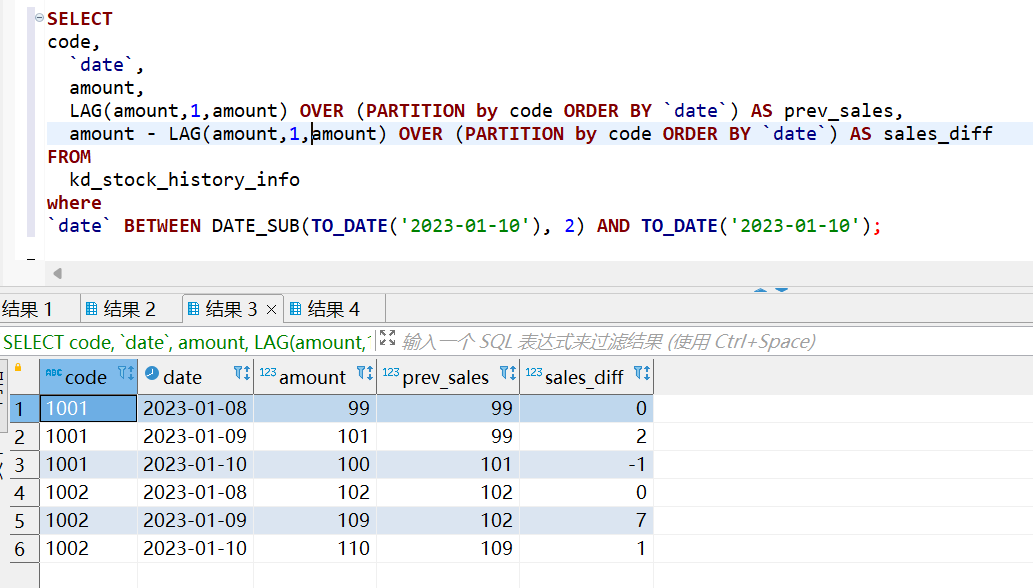
Hive之窗口函数lag()/lead()
一、函数介绍 lag()与lead函数是跟偏移量相关的两个分析函数 通过这两个函数可以在一次查询中取出同一字段的前N行的数据(lag)和后N行的数据(lead)作为独立的列,从而更方便地进行进行数据过滤,该操作可代替表的自联接,且效率更高 lag()/lead() lag(c…...

Vite+Typescript+Vue3学习笔记
ViteTypescriptVue3学习笔记 1、项目搭建 1.1、创建项目(yarn) D:\WebstromProject>yarn create vite yarn create v1.22.19 [1/4] Resolving packages... [2/4] Fetching packages... [3/4] Linking dependencies... [4/4] Building fresh packages...success Installed…...
二、SQL-6.DCL-2).权限控制
*是数据库和表的通配符,出现在数据库位置上表示所有数据库,出现在表名位置上,表示所有表 %是主机名的通配符,表示所有主机。 e.g.所有数据库(*)的所有表(*)的所有权限(a…...

[OpenStack] GPU透传
GPU透传本质就是PCI设备透传,不算是什么新技术。之前按照网上方法都没啥问题,但是这次测试NVIDIA A100遇到坑了。 首先是禁用nouveau 把intel_iommuon rdblacklistnouveau写入/etc/default/grub的cmdline,然后grub2-mkconfig -o /etc/grub2.c…...

无涯教程-jQuery - Progressbar组件函数
小部件进度条功能可与JqueryUI中的小部件一起使用。一个简单的进度条显示有关进度的信息。一个简单的进度条如下所示。 Progressbar - 语法 $( "#progressbar" ).progressbar({value: 37 }); Progressbar - 示例 以下是显示进度条用法的简单示例- <!doctype …...

[SQL挖掘机] - 窗口函数 - rank
介绍: rank() 是一种常用的窗口函数,它为结果集中的每一行分配一个排名(rank)。这个排名基于指定的排序顺序,并且在遇到相同的值时,会跳过相同的排名。 用法: rank() 函数的语法如下: rank() over ([pa…...

VBAC多层防火墙技术的研究-状态检测
黑客技术的提升和黑客工具的泛滥,造成大量的企业、机构和个人的电脑系统遭受程度不同的入侵和攻击,或面临随时被攻击的危险。迫使大家不得不加强对自身电脑网络系统的安全防护,根据系统管理者设定的安全规则把守企业网络,提供强大的、应用选通、信息过滤、流量控制、网络侦…...
PHP8的数据类型-PHP8知识详解
在PHP8中,变量不需要事先声明,赋值即声明。 不同的数据类型其实就是所储存数据的不同种类。在PHP8.0、8.1中都有所增加。以下是PHP8的15种数据类型: 1、字符串(String):用于存储文本数据,可以使…...

明晚直播:可重构计算芯片的AI创新应用分享!
大模型技术的不断升级及应用落地,正在推动人工智能技术发展进入新的阶段,而智能化快速增长和发展的市场对芯片提出了更高的要求:高算力、高性能、灵活性、安全性。可重构计算区别于传统CPU、GPU,以指令驱动的串行执行方式…...
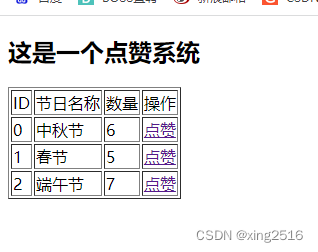
flask 点赞系统
dianzan.html页面 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>点赞系统</title> </head> <body><h2>这是一个点赞系统</h2><table border"1"><…...
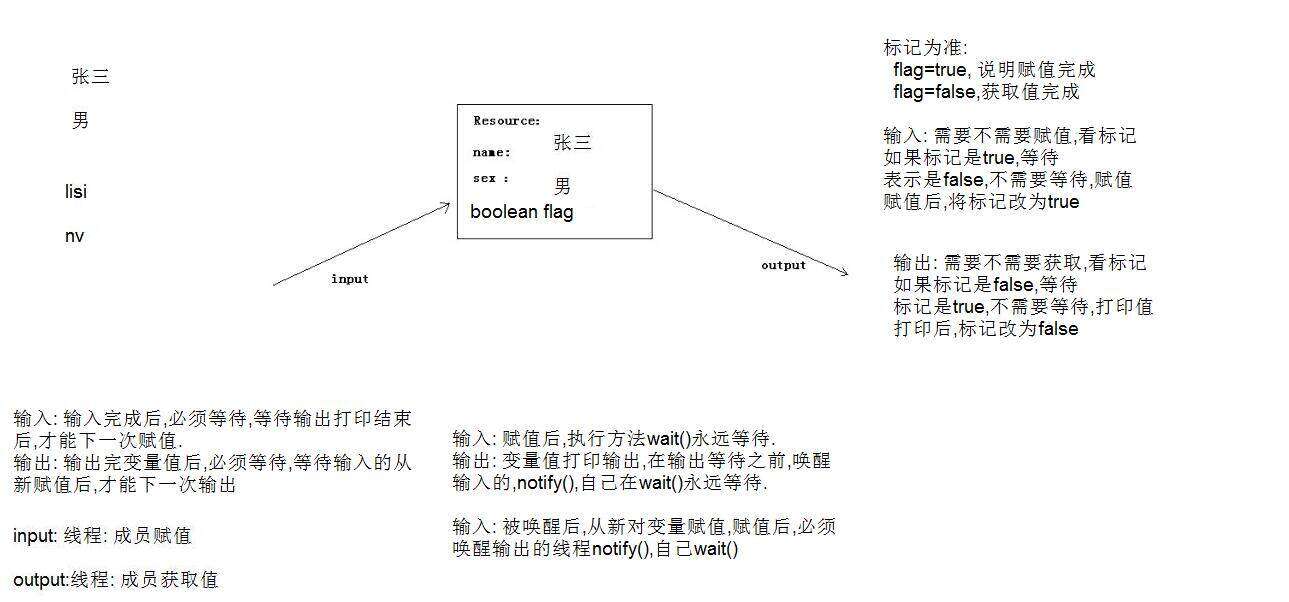
关于Java的多线程实现
多线程介绍 进程:进程指正在运行的程序。确切的来说,当一个程序进入内存运行,即变成一个进程,进程是处于运行过程中的程序,并且具有一定独立功能。 线程:线程是进程中的一个执行单元,负责当前进…...

如何判断某个视频是深度伪造的?
目录 一、前言 二、仔细检查面部动作 三、声音可以提供线索 四、观察视频中人物的身体姿势 五、小心无意义的词语 深造伪造危险吗? 一、前言 制作深度伪造视频就像在Word文档中编辑文本一样简单。换句话说,您可以拍下任何人的视频,让他…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

若依登录用户名和密码加密
/*** 获取公钥:前端用来密码加密* return*/GetMapping("/getPublicKey")public RSAUtil.RSAKeyPair getPublicKey() {return RSAUtil.rsaKeyPair();}新建RSAUti.Java package com.ruoyi.common.utils;import org.apache.commons.codec.binary.Base64; im…...
