剑指offer10-I.斐波那契数列

学计算机的对这道题肯定不陌生,我记得是学C语言的时候学递归的时候有这道题,于是我就世界用递归写了如下代码:
class Solution {public int fib(int n) {if(n==1) return 1;if(n==0) return 0;return (fib(n-1) + fib(n-2)) % 1000000007;}
}到n=44就算不出了,超时了。就看了一下题解,题解用的是动态规划的方法:
class Solution {public int fib(int n) {if(n<2){return n;}int p=0,q=1;int r =0;for(int i =2;i<=n;i++){r = (p+q) % 1000000007;p = q;q = r; }return r;}
}n小于2的话返回自己,然后定义p为n的前两个数,q为n的前一个数,然后r是第n个数的值,所以r就等于p+q,然后把q给p,r给q,最后返回r就可以了。
题解还给出了一种矩阵幂的方法:

最后只需要求M的n次方就行。
class Solution {static final int MOD = 1000000007;public int fib(int n) {if (n < 2) {return n;}int[][] q = {{1, 1}, {1, 0}};int[][] res = pow(q, n - 1);return res[0][0];}public int[][] pow(int[][] a, int n) {int[][] ret = {{1, 0}, {0, 1}};while (n > 0) {if ((n & 1) == 1) {ret = multiply(ret, a);}n >>= 1;a = multiply(a, a);}return ret;}public int[][] multiply(int[][] a, int[][] b) {int[][] c = new int[2][2];for (int i = 0; i < 2; i++) {for (int j = 0; j < 2; j++) {c[i][j] = (int) (((long) a[i][0] * b[0][j] + (long) a[i][1] * b[1][j]) % MOD);}}return c;}
}定义了一个矩阵乘矩阵的multiply方法,求矩阵的n次方的pow方法,通过这两个方法可以求出M的n次方。
相关文章:

剑指offer10-I.斐波那契数列
学计算机的对这道题肯定不陌生,我记得是学C语言的时候学递归的时候有这道题,于是我就世界用递归写了如下代码: class Solution {public int fib(int n) {if(n1) return 1;if(n0) return 0;return (fib(n-1) fib(n-2)) % 1000000007;} } 到…...
13年测试经验,性能测试-压力测试指标分析总结,看这篇就够了...
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 一般推荐…...

大数据课程D3——hadoop的Source
文章作者邮箱:yugongshiye@sina.cn 地址:广东惠州 ▲ 本章节目的 ⚪ 掌握Source的AVRO Source; ⚪ 掌握Source的Exec Source; ⚪ 掌握Source的Spooling Directory Source; ⚪ 掌握Source的Netcat Source; ⚪ 掌握Source的Sequence Generator Source;…...
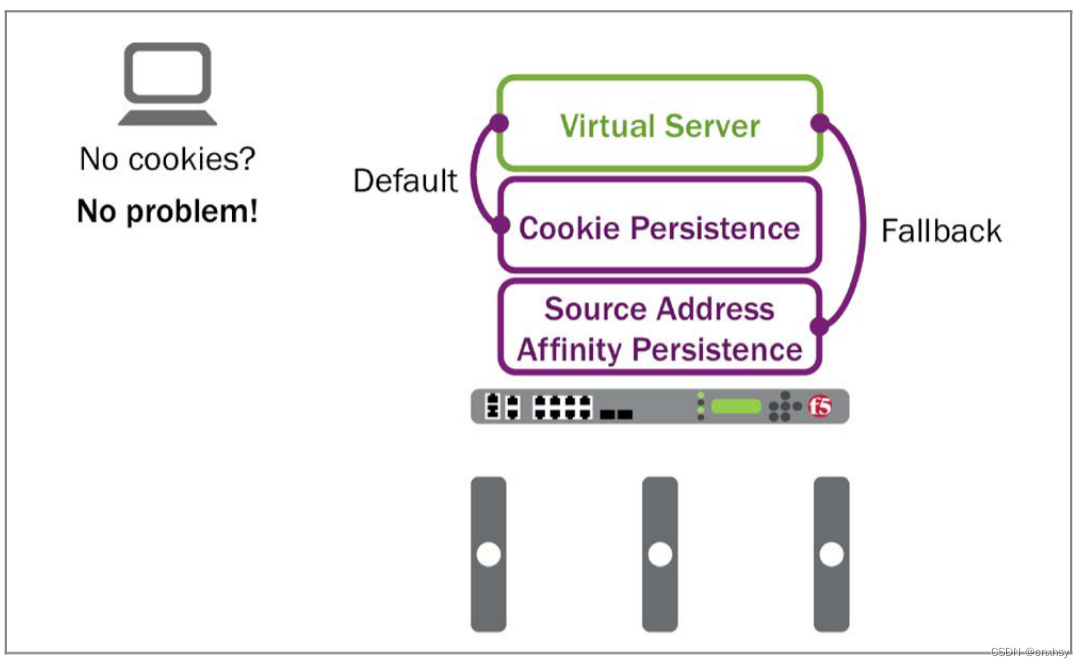
F5 LTM 知识点和实验 4-持久化
第四章:持久化 持久化: 大多数应用都是有状态的,比如,使用一个购物网站,最重要的是用户在放入一个商品之后,刷新网页要能继续看到购物车里的东西,这就需要请求报文发到同一个后端服务器上,持久化就能完成这个功能。 持久化支持一下几种场景: 源地址目标地址SSLSIPH…...

SpringBoot之WebMvcConfigurer详解
目录 一、基本介绍 二、WebMvcConfigurer接口展示 三、常用方法列举 3.1 addInterceptors:添加拦截器 3.2 addResourceHandlers:添加静态资源 3.3 addCorsMappings:添加跨域 编写的初衷是为了自己巩固复习,如果能帮到你将是…...

WPF实战学习笔记22-添加自定义询问窗口
添加自定义询问窗口 详细代码:https://github.com/DongLiqiang/Mytodo/commit/221de6b2344d5c861f1d3b2fbb2480e3e3b35c26 添加自定义询问窗口显示方法 修改文件Mytodo.Extensions.DialogExtension 添加内容,类中添加内容 /// <summary> /// …...

Spring Boot项目的创建
hi 大家好,又见面了,今天继续讲解Spring Boot 文章目录 🐶1.什么是Spring Boot?🐶2.Spring Boot的优势🐶3.Spring Boot项目创建🌼3.1使用ieda创建🥝3.1.1下载插件Spring Boot Helper🥝3.1.2创建项目 &…...

Python加载数据的5种方法
大家好,今天回顾五种引入数据的Python技术,并附有代码实例参考。 我们将使用Numpy、Pandas和Pickle包,所以要导入它们: import numpy as np import pandas as pd import pickle Manual功能 这是最困难的,因为你必须…...
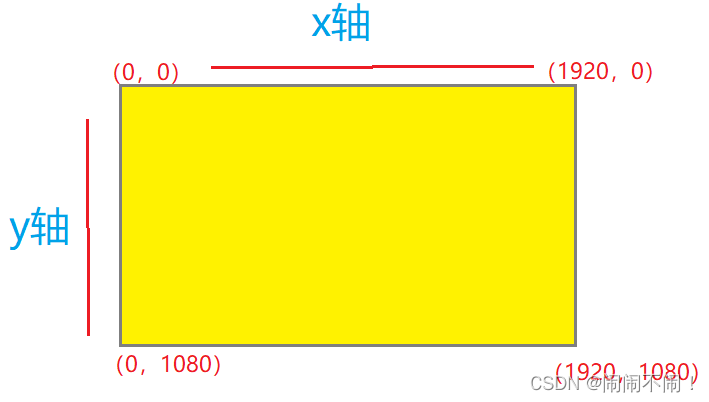
QPoint、QLine、QSize、QRect
QPoint、QLine、QSize、QRect QPointQLineQSizeQRect QPoint // 构造函数 // 构造一个坐标原点, 即(0, 0) QPoint::QPoint(); // 参数为 x轴坐标, y轴坐标 QPoint::QPoint(int xpos, int ypos);// 设置x轴坐标 void QPoint::setX(int x); // 设置y轴坐标 void QPoint::setY(in…...
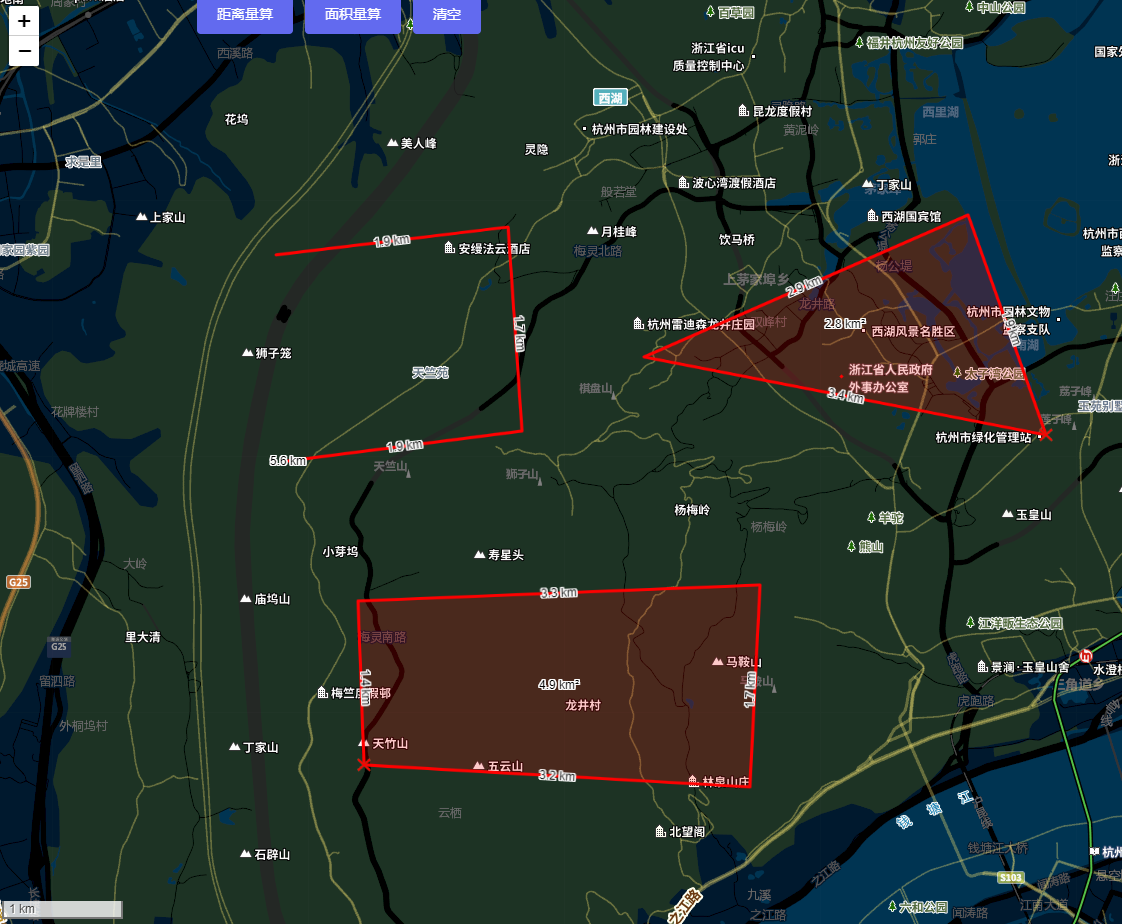
vue+leaflet笔记之地图量测
vueleaflet笔记之地图量测 文章目录 vueleaflet笔记之地图量测开发环境代码简介插件简介与安装使用简介图形量测动态量测 详细源码(Vue3) 本文介绍了Web端使用Leaflet开发库进行距离量测的一种方法 (底图来源:天地图),结合leaflet-measure-path插件能够快速的实现地…...

“深入理解SpringBoot:从入门到精通的几个关键要点“
标题:深入理解Spring Boot:从入门到精通 摘要:本文将深入探讨Spring Boot的关键要点,帮助读者从入门到精通。我们将从Spring Boot的基本概念开始,介绍自动配置、起步依赖、注解驱动开发等特性,并通过示例代…...
数值线性代数: 共轭梯度法
本文总结线性方程组求解的相关算法,特别是共轭梯度法的原理及流程。 零、预修 0.1 LU分解 设,若对于,均有,则存在下三角矩阵和上三角矩阵,使得。 设,若对于,均有,则存在唯一的下三…...
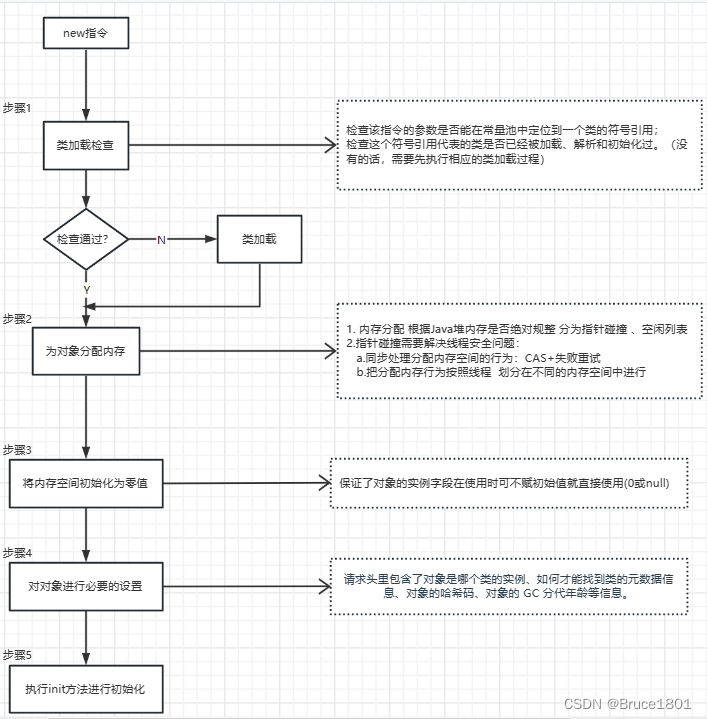
【JVM】详解对象的创建过程
文章目录 1、创建对像的几种方式1、new关键字2、反射3、clone4、反序列化 2、创建过程步骤 1、检查类是否已经被加载步骤 2、 为对象分配内存空间1、指针碰撞针对指针碰撞线程不安全,有两种方案: 2、空闲列表选择哪种分配方式 步骤3、将内存空间初始化为…...

华纳云:ubuntu下如何搭建nfs服务
在Ubuntu下搭建NFS(Network File System)服务,可以实现网络文件共享。以下是在Ubuntu上搭建NFS服务的步骤: 安装NFS服务器和客户端软件: 打开终端,并使用以下命令安装NFS服务器和客户端软件: sudo apt-get update s…...
HCIA实验二
实验要求: 1.R2为ISP,只能配置IP 2.R1-R2之间为HDLC封装 3.R2-R3之间为PPP封装,pap认证,R2为主认证方 4.R2-R4之间为PPP封装,chap认证,R2为主认证方 5.R1、R2、R3构建MGRE,仅R1的IP地址固定…...
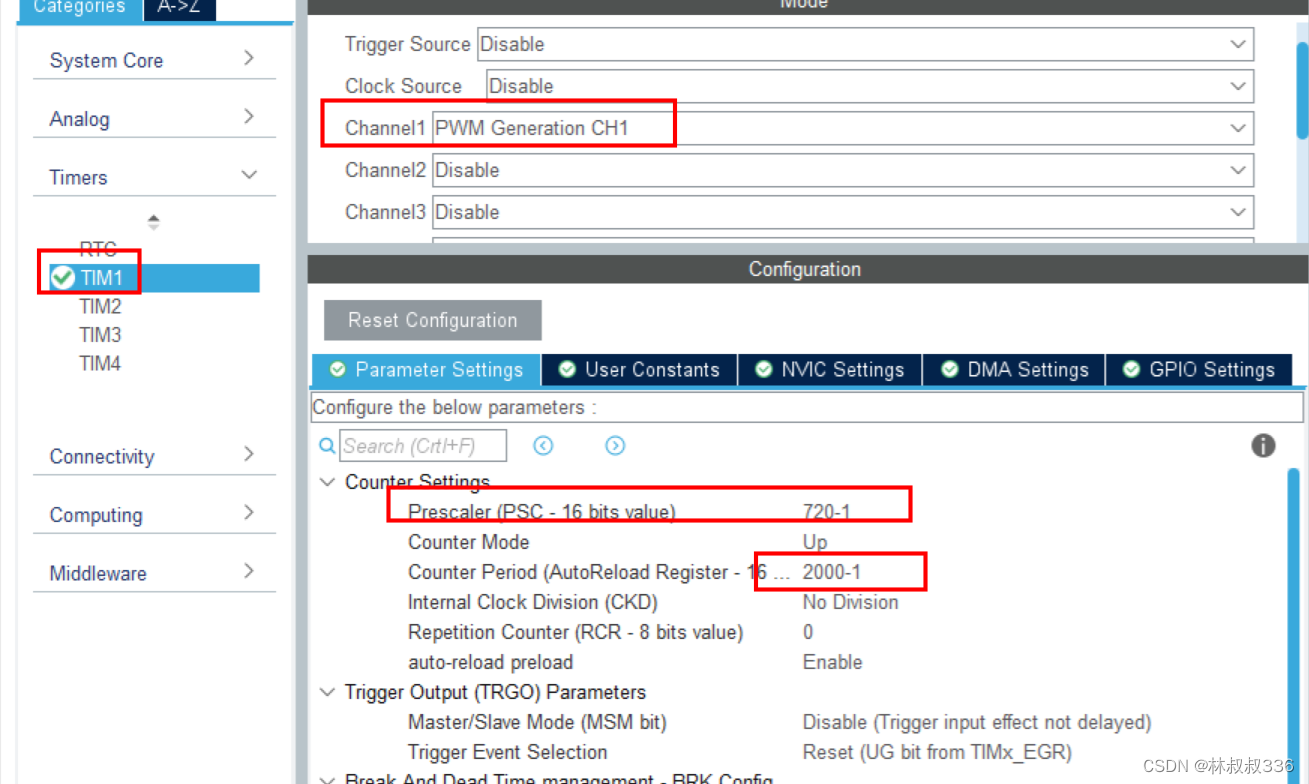
stm32 舵机 cubemx
文章目录 前言一、cubemx配置二、代码1.serve.c2.serve.h3.主函数 总结 前言 stm32对舵机进行控制,很简单直接一个pwm就可以实现 pwm的周期是50HZ占空比分别对应 一个0.5ms的高电平对应于0度 一个1.5ms的高电平对应于90度 一个2.5ms的高电平对应于180度 因此&#…...

无涯教程-jQuery - Spinner组件函数
Widget Spinner 函数可与JqueryUI中的窗口小部件一起使用。Spinner提供了一种从一组中选择一个值的快速方法。 Spinner - 语法 $( "#menu" ).selectmenu(); Spinner - 示例 以下是显示Spinner用法的简单示例- <!doctype html> <html lang"en"…...
Python 有趣的模块之pynupt——通过pynput控制鼠标和键盘
Python 有趣的模块之pynupt ——通过pynput控制鼠标和键盘 文章目录 Python 有趣的模块之pynupt ——通过pynput控制鼠标和键盘1️⃣简介2️⃣鼠标控制与移动3️⃣键盘控制与输入4️⃣结语📢 1️⃣简介 🚀🚀🚀学会控制鼠标和键盘是…...

docker基于centos7镜像安装python3.7.9
下载centos7镜像 docker pull centos:centos7 启动容器centos-python-3.7 docker run -itd --name centos-python-3.7 -p 60021:22 --privileged centos:centos7 /usr/sbin/init 进入容器 docker exec -it centos-python-3.7 /bin/bash centos7环境下安装python3.7.…...

JavaScript中的switch语句
switch语句和if语句一样,同样是运用于条件循环中; 下面例子我们用switch实现 例如如果今天是周一就学习HTML,周二学习CSS和JavaScript,周三学习vue,周四,周五学习node.js,周六周日快乐玩耍&…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

Vue3中的computer和watch
computed的写法 在页面中 <div>{{ calcNumber }}</div>script中 写法1 常用 import { computed, ref } from vue; let price ref(100);const priceAdd () > { //函数方法 price 1price.value ; }//计算属性 let calcNumber computed(() > {return ${p…...

Canal环境搭建并实现和ES数据同步
作者:田超凡 日期:2025年6月7日 Canal安装,启动端口11111、8082: 安装canal-deployer服务端: https://github.com/alibaba/canal/releases/1.1.7/canal.deployer-1.1.7.tar.gz cd /opt/homebrew/etc mkdir canal…...
