数值线性代数: 共轭梯度法
本文总结线性方程组求解的相关算法,特别是共轭梯度法的原理及流程。
零、预修
0.1 LU分解
设,若对于
,均有
,则存在下三角矩阵
和上三角矩阵
,使得
。
设,若对于
,均有
,则存在唯一的下三角矩阵
和上三角矩阵
,使得
,并且
。
0.2 Cholesky分解
若对称正定,则存在一个对角元均为正数的下三角矩阵
,使得
。
一、 总论:迭代法求解线性方程组的一般思路
对于非奇异矩阵,
,使用迭代法求解线性方程组
过程中,一般需要以下流程进行:
- 给定一个初始向量
;
- 构造一个递推公式
;
- 不断递推
,使其近似收敛于
;
下表列出了若干迭代算法的迭代公式。
| 方法 | 迭代公式 | 备注 | |
| Jacobi迭代 | 非奇异 | ||
| Gausss-Seidel迭代 | 非奇异 | ||
| SOR迭代 | 非奇异 | ||
| Steepest Descent | 对称正定 | ||
| Conjugate Gradient | 对称正定 | 当 当 |
二、Projection Method
投影法将线性方程组求解问题转换成了最优值求解问题,是求解线性方程组的一大类方法。
在投影法中,令,构造列满秩矩阵
与
,寻找
,满足Petrov-Galerkin条件,即
,均有
。
称为搜索空间,
称为约束空间。若
时,称为正投影算法,否则称为斜投影算法。
三、Krylov Subspace Method
Krylov子空间法本质上也是一种投影法,其核心思想是在更小维度的Krylov子空间内寻找满足精度要求的近似解。即令,构造了
维Krylov子空间
,使得
。
选择不同的,就对应不同的Krylov子空间法。
3.1 Steepest Descent Method
3.2 Hestenes-Stiefel Conjugate Gradient Method
3.3 Preconditioned Conjugate Gradient
参考书籍
Golub G H , Loan C F V .Matrix Computations.Johns Hopkins University Press,1996.
Ford W .Numerical Linear Algebra with Applications using MATLAB. 2014.
徐树方. 数值线性代数(第二版). 北京大学出版社, 2010.
参考文献
Hestenes M R , Stiefel E L .Methods of Conjugate Gradients for Solving Linear Systems. Journal of Research of the National Bureau of Standards (United States), 1952.
相关文章:
数值线性代数: 共轭梯度法
本文总结线性方程组求解的相关算法,特别是共轭梯度法的原理及流程。 零、预修 0.1 LU分解 设,若对于,均有,则存在下三角矩阵和上三角矩阵,使得。 设,若对于,均有,则存在唯一的下三…...
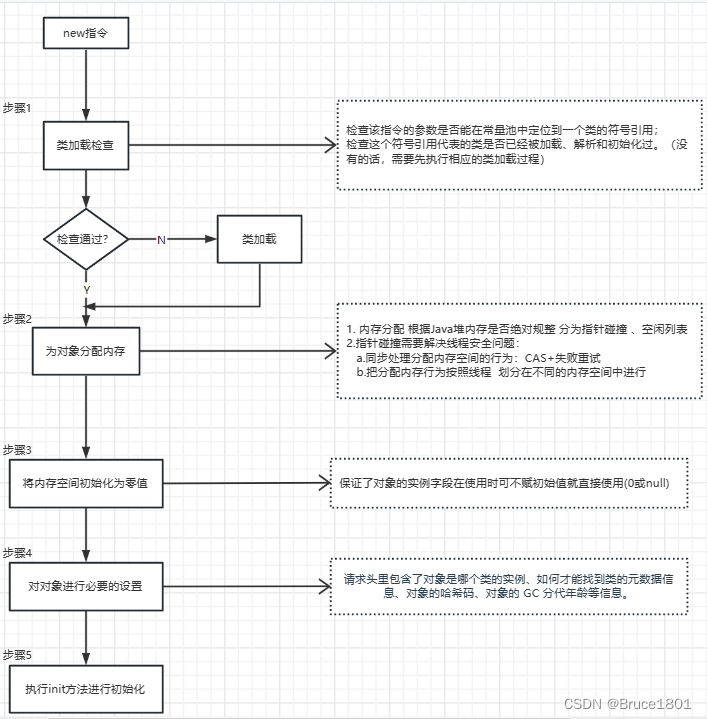
【JVM】详解对象的创建过程
文章目录 1、创建对像的几种方式1、new关键字2、反射3、clone4、反序列化 2、创建过程步骤 1、检查类是否已经被加载步骤 2、 为对象分配内存空间1、指针碰撞针对指针碰撞线程不安全,有两种方案: 2、空闲列表选择哪种分配方式 步骤3、将内存空间初始化为…...

华纳云:ubuntu下如何搭建nfs服务
在Ubuntu下搭建NFS(Network File System)服务,可以实现网络文件共享。以下是在Ubuntu上搭建NFS服务的步骤: 安装NFS服务器和客户端软件: 打开终端,并使用以下命令安装NFS服务器和客户端软件: sudo apt-get update s…...
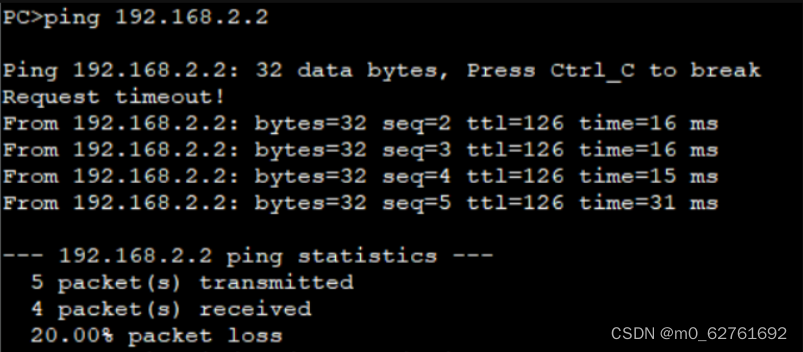
HCIA实验二
实验要求: 1.R2为ISP,只能配置IP 2.R1-R2之间为HDLC封装 3.R2-R3之间为PPP封装,pap认证,R2为主认证方 4.R2-R4之间为PPP封装,chap认证,R2为主认证方 5.R1、R2、R3构建MGRE,仅R1的IP地址固定…...
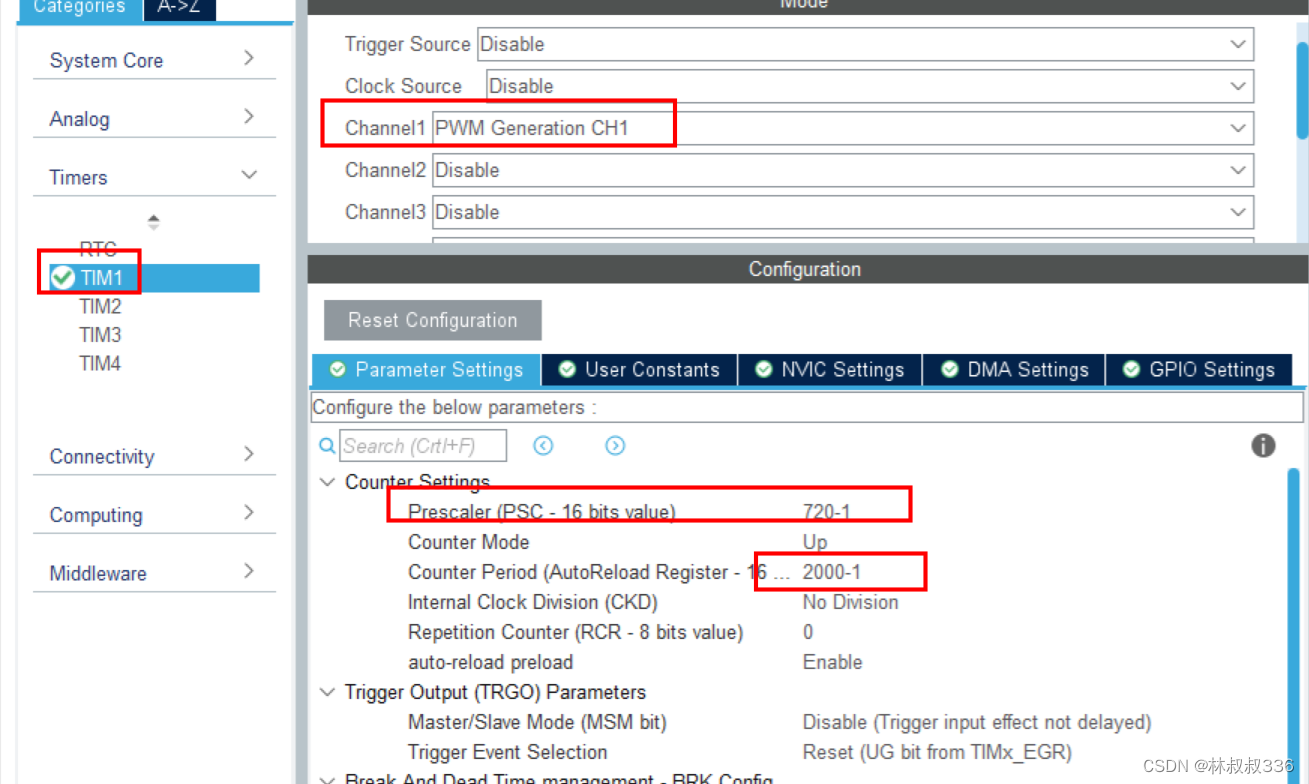
stm32 舵机 cubemx
文章目录 前言一、cubemx配置二、代码1.serve.c2.serve.h3.主函数 总结 前言 stm32对舵机进行控制,很简单直接一个pwm就可以实现 pwm的周期是50HZ占空比分别对应 一个0.5ms的高电平对应于0度 一个1.5ms的高电平对应于90度 一个2.5ms的高电平对应于180度 因此&#…...

无涯教程-jQuery - Spinner组件函数
Widget Spinner 函数可与JqueryUI中的窗口小部件一起使用。Spinner提供了一种从一组中选择一个值的快速方法。 Spinner - 语法 $( "#menu" ).selectmenu(); Spinner - 示例 以下是显示Spinner用法的简单示例- <!doctype html> <html lang"en"…...
Python 有趣的模块之pynupt——通过pynput控制鼠标和键盘
Python 有趣的模块之pynupt ——通过pynput控制鼠标和键盘 文章目录 Python 有趣的模块之pynupt ——通过pynput控制鼠标和键盘1️⃣简介2️⃣鼠标控制与移动3️⃣键盘控制与输入4️⃣结语📢 1️⃣简介 🚀🚀🚀学会控制鼠标和键盘是…...

docker基于centos7镜像安装python3.7.9
下载centos7镜像 docker pull centos:centos7 启动容器centos-python-3.7 docker run -itd --name centos-python-3.7 -p 60021:22 --privileged centos:centos7 /usr/sbin/init 进入容器 docker exec -it centos-python-3.7 /bin/bash centos7环境下安装python3.7.…...

JavaScript中的switch语句
switch语句和if语句一样,同样是运用于条件循环中; 下面例子我们用switch实现 例如如果今天是周一就学习HTML,周二学习CSS和JavaScript,周三学习vue,周四,周五学习node.js,周六周日快乐玩耍&…...

Jquery笔记
DOM对象通过jquery获取 所有的代码都是基于引入jquery.js文件 var mydiv $(#div);//直接获取到DOM对象元素id var mydiv$(.div);//通过class获取DOM对象,如果有同名class只会获取第一个 var mysapn$(span);//通过元素的标签名获取DOM对象 var divarr$(…...
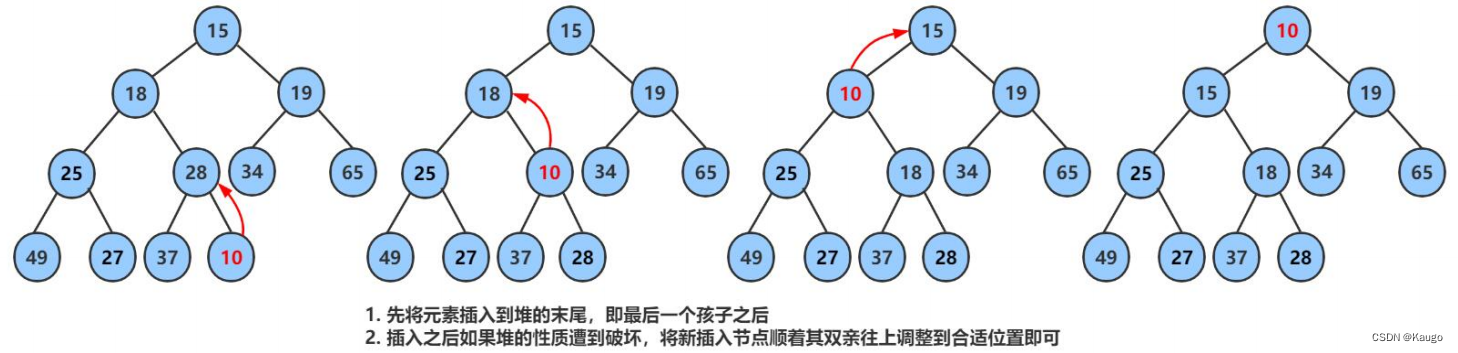
【C++】优先级队列的基本概念以及其模拟实现
文章目录 补充知识:仿函数一、优先级队列:1.引入2.介绍 二、priority_queue的模拟实现1.大体框架2.私有成员函数:1.向下调整(AdjustDown)2.向上调整(AdjustUp) 3.公有成员函数1大小(…...
TextClamp for Vue3.0(Vue3.0的文本展开收起组件)
呦!大家好,好久没有更新博客了,最近实现了一个一直想自己完成的一个东西,就是文本的展开收起组件,以前项目需要用到,自己实现一个又太繁琐,所以那个时候都是用的别人的轮子,现在自己…...

区间预测 | MATLAB实现VAR向量自回归时间序列区间预测
区间预测 | MATLAB实现VAR向量自回归时间序列区间预测 目录 区间预测 | MATLAB实现VAR向量自回归时间序列区间预测预测效果基本介绍程序设计参考资料预测效果 基本介绍 区间预测 | MATLAB实现VAR向量自回归时间序列区间预测 VAR(Vector Autoregression)模型是一种广泛应用于时…...

在 Windows 上搭建 NTP 服务器
文章目录 一、基础环境二、适用场景三、操作步骤四、常用的NTP服务器五、参考资料 版权声明:本文为博主原创文章,于2023年7月30日首发于CSDN,转载请附上原文出处链接和本声明。本文链接:https://blog.csdn.net/u011046671 一、基础…...
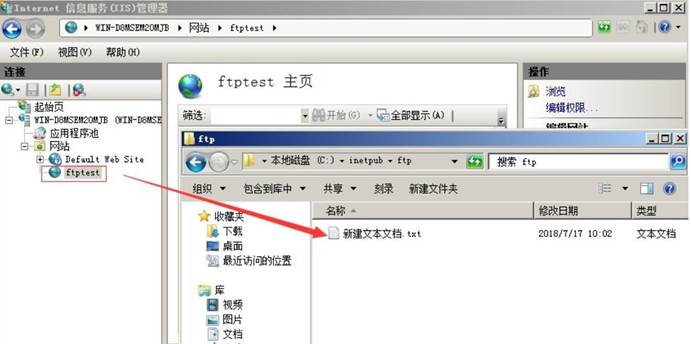
应急响应经典案例-FTP 暴力破解
应急响应经典案例-FTP 暴力破解 应急场景日志分析应急处理措施 应急场景 从昨天开始,网站响应速度变得缓慢,网站服务器登录上去非常卡,重启服务器就能保证一段时间的正常访问,网站响应状态时而飞快时而缓慢,多数时间是…...

41. linux通过yum安装postgresql
文章目录 1.下载安装包2.关闭内置PostgreSQL模块:3.安装postgresql服务:4.初始化postgresql数据库:5.设置开机自启动:6.启动postgresql数据库7.查看postgresql进程8.通过netstat命令或者lsof 监听默认端口54329.使用find命令查找了一下postgresql.conf的配置位置10.修改postgre…...

SpringBoot启动流程及自动配置
SpringBoot启动流程源码: 1、启动SpringBoot启动类SpringbootdemoApplication中的main方法。 SpringBootApplication public class SpringbootdemoApplication {public static void main(String[] args) {SpringApplication.run(SpringbootdemoApplication.class, …...

【Linux】进程轻松入门
目录 一, 冯* 诺依曼体系结构 1,存储结构 编辑 二, 操作系统 1,概念 2,设计OS的目的 3,定位 4,如何理解 "管理" 5, 总结 三,进程 1. 概念 那么…...
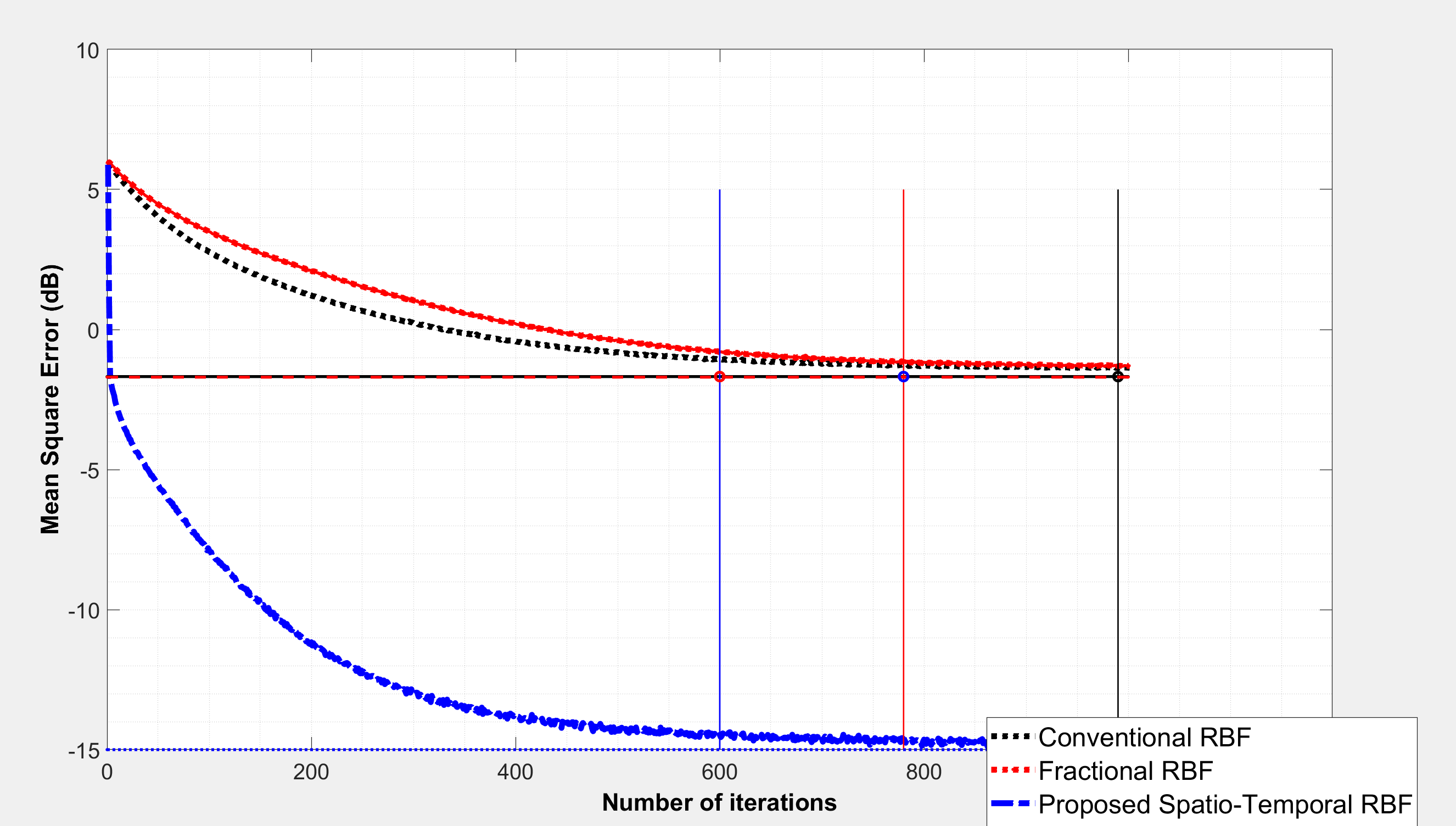
【使用时空RBF-NN进行非线性系统识别】实现了 RBF、分数 RBF 和时空 RBF 神经网络,用于非线性系统识别研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

Tomcat 安装配置教程及成功后,启动失败报错解决方案
解决方案 我的报错原因是因为我的JDK是1.8的而我的Tomcat是10版本的,可能是因为版本原因吧,我重新装了Tomcat 9就可以启动成功了! 简单说下安装的时候需要注意哪些步骤吧 今天我在安装tomcat10的时候,安装成功后,启…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...
