Linux软件管理YUM
目录
yum配置文件
创建仓库
yum查询功能
yum安装与升级功能
yum删除功能
yum仓库产生的问题和解决之道
yum与dnf
网络源
YUM就是通过分析RPM的标头数据后,根据各软件的相关性制作出属性依赖时的解决方案,然后可以自动处理软件的依赖属性问题,以解决软件安装或删除与升级的问题
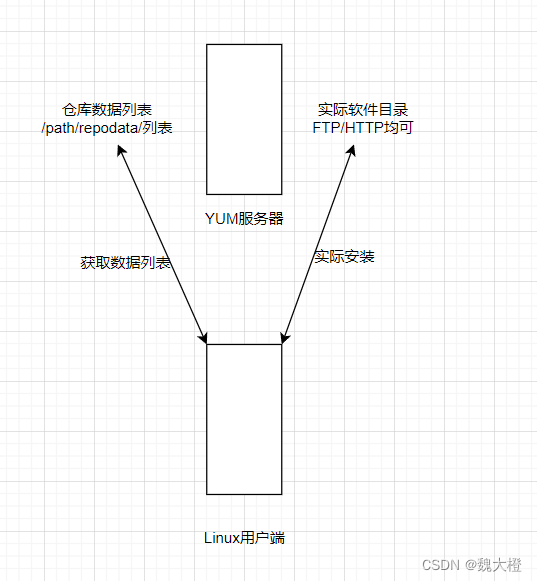
发布的软件先放置到YUM服务器内,然后分析这些软件的依赖属性问题,将软件内的记录信息记录下来(header),然后再将这些信息分析后记录成软件相关性的列表,这些列表数据与软件所在的主机或网络上的位置可称为软件源或软件仓库(repository)
当客户端有软件安装、升级的需求时,客户端主机会主动的从网络上面的YUM服务器的软件源地址下载列表,然后通过列表的数据与本机RPM数据库已存在的软件数据相比较,就能够一口气安装所有需要的具有依赖性的软件了
yum配置文件
yum的配置文件分为两部分:全局配置文件和yum仓库配置文件
全局配置文件只有一个,定义了yum根据的一些全局配置选项,一般位于/etc/yum.conf中
![]()
yum仓库(软件源)有三个存放地址
- /etc/yum.repos.d
- /etc/yum/repos.d
- /etc/distro.repos.d
仓库配置文件必须以 .repo结尾
系统中自带一个redhat.repo文件,里面并没有实际内容

创建仓库
创建仓库只需在三个目录下创建一个以.repo结尾的文件即可
![]()

仓库内容格式:
- [base]:代表软件源的名称,名称可以随便取,但是不能有两个相同的软件源名称
- name=:描述,说明一下软件源的意义
- baseurl=:软件源的实际地址,指定到源数据路径即可
- enable=:是否启动此软件源
- gpgcheck=:是否启动验证(查看RPM文件内的数字签名)
- gpgkey=:数字签名的公钥文件所在文件(当不启动验证时可不写)
- mirrorlist=:这个软件源的镜像站(可不写)
baseurl有三种写法:
- file://
- http://
- ftp://
查看一下我们的仓库:

此时我们可以检验一下我们的仓库是否可用
先把光盘挂载一下:
我们之前使用yum安装httpd是失败的,因为仓库中没有此软件和依赖软件(路径中就没有仓库)
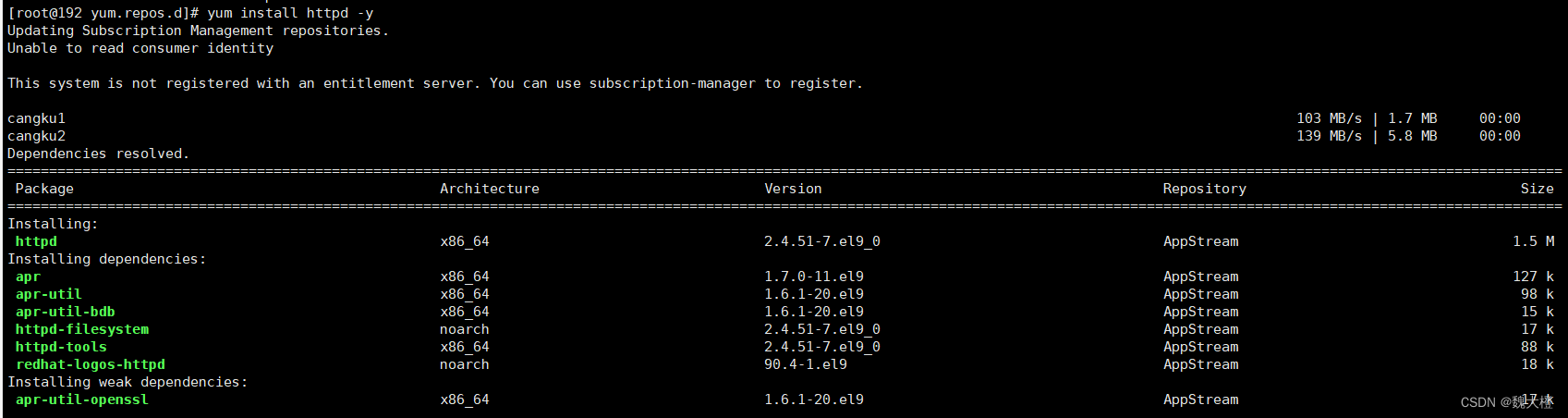
配置完仓库后,我们再来试试
它把所有此软件以及依赖关系的软件全部安装了
yum查询功能
yum 【option】【查询工作选项】【相关参数】
选项与参数:
-y:当yum等待输入时,这个选项可以自动提供yes回应
查询工作选项 相关参数:
search:查找出某个软件名称或是描述(description)的重要关键字
list:列出目前yum所管理的所有软件与版本,有点类似rpm -qa
info:同上,有点类似rpm -qai
provides:从文件去查找软件,类似rpm -qf的功能
查找mdadm软件的功能
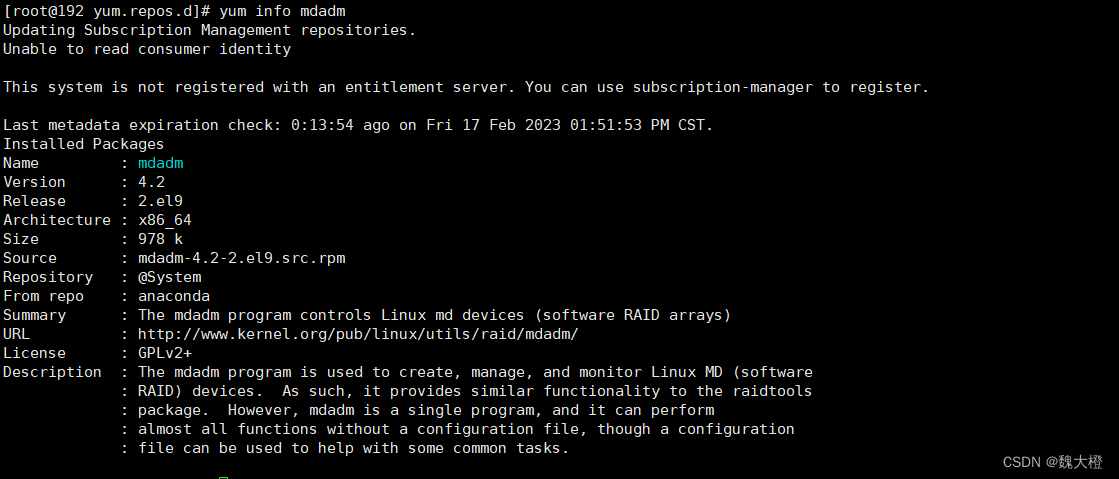
列出可升级的软件:yum list update
yum安装与升级功能
使用install与update这两个参数处理即可
yum 【install/update】软件
选项与参数:
install:后面接要安装的软件
update:后面接要升级的软件
yum删除功能
yum remove 软件
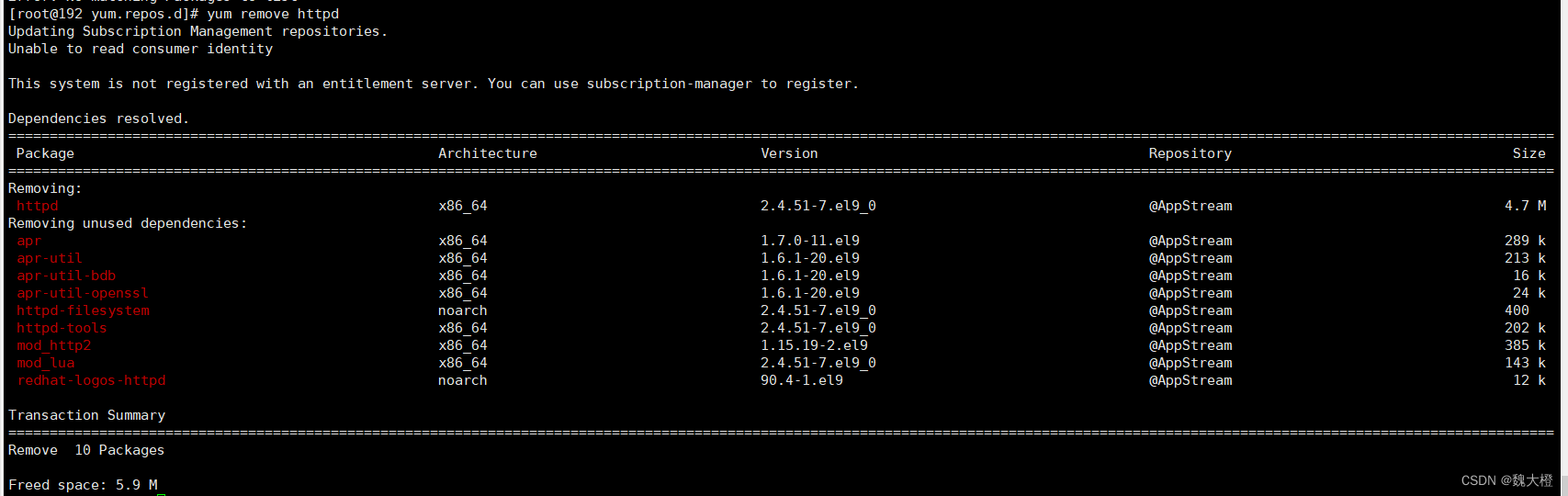
yum仓库产生的问题和解决之道
仓库技术就是软件源,但是由于使用的软件源有新旧之分,因此当我们的仓库与源数据存放路径的数据不同步时,此时会出现无法更新等问题
处理方法:通过yum的clean选项来处理即可
yum clean 【packages/headers/all】
选项与参数:
packages:将已下载的安装文件删除
headers:将下载的安装文件头删除
all:将所有软件源数据都删除
yum与dnf
在yum机制,仍然存在一些问题,如分析不准确,占用内存量大,不能多人同时安装软件等硬伤
所以在新版本Fedora 22系统的发布后,redhat公司给了我们一个dnf命令,它实际上就是yum的升级版,也称为yum v4版本,它们都是同样的使用方式,只需把yum换为dnf即可


网络源
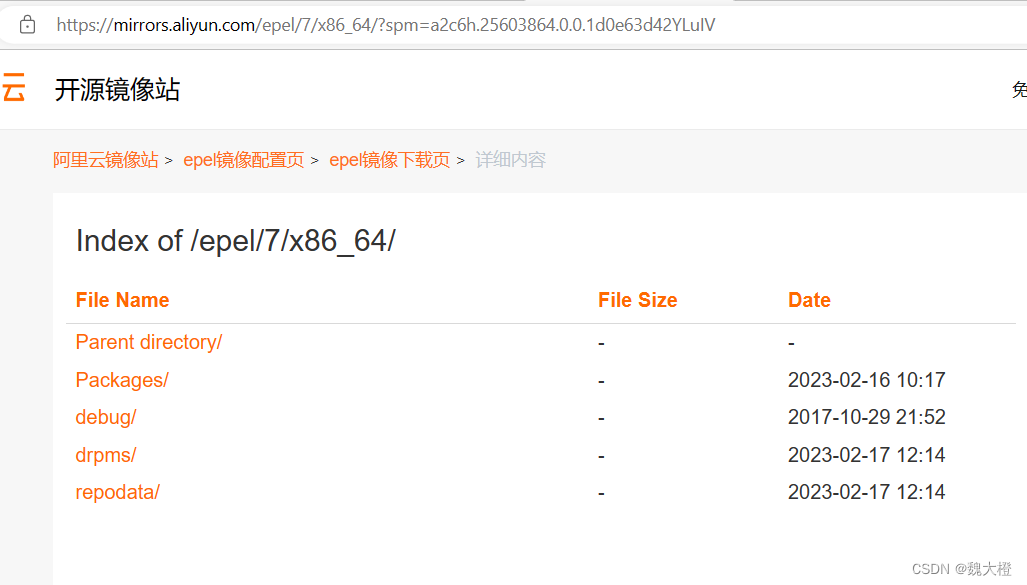
网络源即网络上的仓库,网络上搜索epel即可
网址中最具特色的是repodata目录,该目录时分析RPM软件后产生的软件属性依赖数据存放处,因此找软件源所在目录时,该地址下面必须有个repodata的目录存在
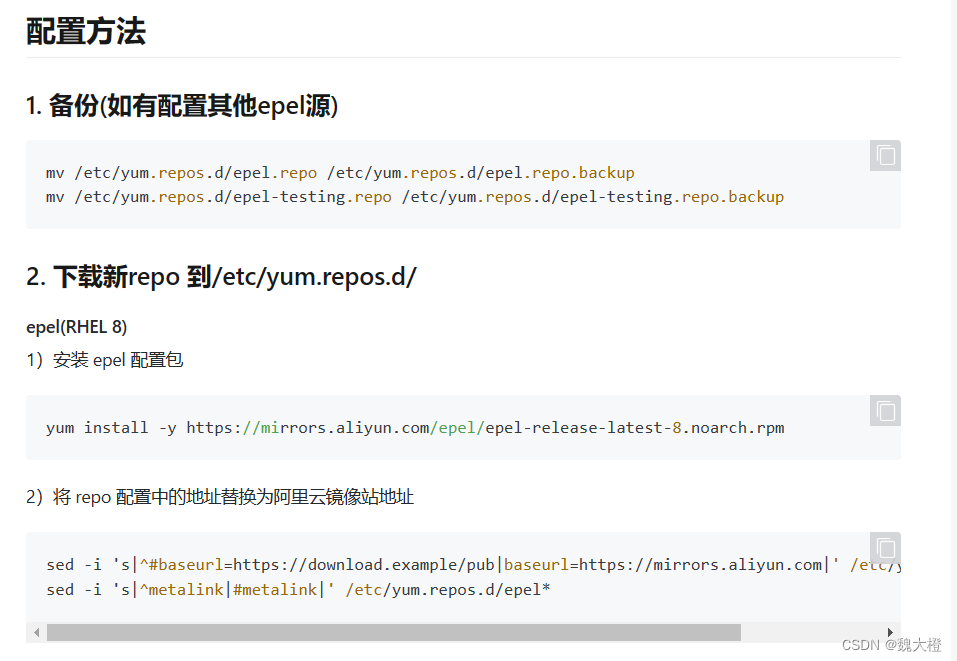
会有配置方法告诉你如何安装
因为我使用的是RHEL9(官网进不去,镜像还没有方便的配置方法),找到的此目录
然后手动创建了一个仓库
实际使用也是可用的
相关文章:

Linux软件管理YUM
目录 yum配置文件 创建仓库 yum查询功能 yum安装与升级功能 yum删除功能 yum仓库产生的问题和解决之道 yum与dnf 网络源 YUM就是通过分析RPM的标头数据后,根据各软件的相关性制作出属性依赖时的解决方案,然后可以自动处理软件的依赖属性问题&…...
【自学MYSQL】MySQL Windows安装
MySQL Windows安装 MySQL Windows下载 首先,我们打开 MySQL 的官网,网址如下: https://dev.mysql.com/downloads/mysql/在官网的主页,我们首先根据我们的操作系统,选择对应的系统,这里我们选择 Windows&…...

Linux c编程之常用技巧
一、说明 在Linux C的实际编程应用中,有很多有用的实践技巧,编程中掌握这些知识,会对编程有事半功倍的效果。 二、常用技巧 2.1 if 变量条件的写法 main.c: #include <stdio.h>int main(int argc, char *argv[]) {int a =...
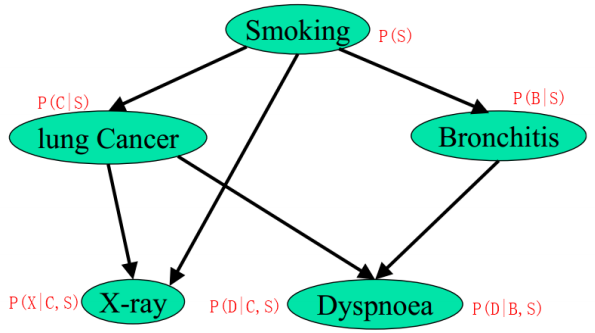
21- 朴素贝叶斯 (NLP自然语言算法) (算法)
朴素贝叶斯要点 概率图模型算法往往应用于NLP自然语言处理领域。根据文本内容判定 分类 。 概率密度公式: 高斯朴素贝叶斯算法: from sklearn.naive_bayes import GaussianNB model GaussianNB() model.fit(X_train,y_train) 伯努利分布朴素贝叶斯算法 fro…...
设计模式第七讲-外观模式、适配器模式、模板方法模式详解
一. 外观模式 1. 背景 在现实生活中,常常存在办事较复杂的例子,如办房产证或注册一家公司,有时要同多个部门联系,这时要是有一个综合部门能解决一切手续问题就好了。 软件设计也是这样,当一个系统的功能越来越强&…...
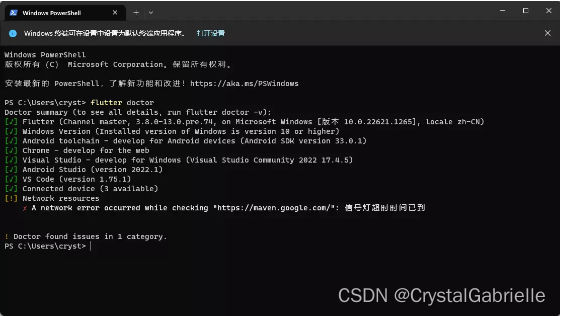
flutter-第1章-配置环境
flutter-第1章-配置环境 本文针对Windows系统。 一、安装Android Studio 从Android Studio官网下载最新版本,一直默认安装就行。 安装完成要下载SDK,可能会需要科学上网。 打开AS,随便创建一个新项目。 点击右上角的SDK Manager 找到SDK…...
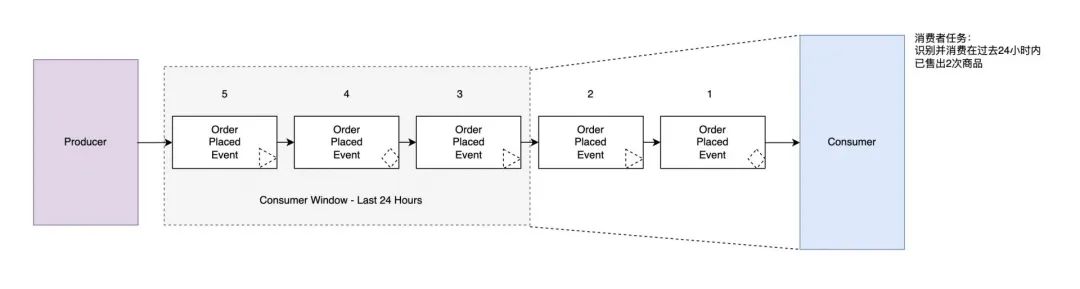
“消息驱动、事件驱动、流 ”的消息模型
文章目录背景消息驱动 Message-Driven事件驱动 Event-Driven流 Streaming事件规范标准简介: 本文旨在帮助大家对近期消息领域的高频词“消息驱动(Message-Driven),事件驱动(Event-Driven)和流(S…...

量化股票配对交易可以用Python语言实现吗?
量化股票配对交易可以用Python语言实现吗?Python 是一种流行的编程语言,可用于所有类型的领域,包括数据科学。有大量软件包可以帮助您实现目标,许多公司使用 Python 来开发与金融界相关的以数据为中心的应用程序和科学计算。 最重…...

机器学习洞察 | 一文带你“讲透” JAX
在上篇文章中,我们详细分享了 JAX 这一新兴的机器学习模型的发展和优势,本文我们将通过 Amazon SageMaker 示例展示如何部署并使用 JAX。JAX 的工作机制JAX 的完整工作机制可以用下面这幅图详细解释:图片来源:“Intro to JAX” video on YouT…...
OpenFaaS介绍
FaaS 云计算时代出现了大量XaaS形式的概念,从IaaS(Infrastructure as a Service)、PaaS(Platform as a Service)、SaaS(Software as a Service)到容器云引领的CaaS(Containers as a Service),再到火热的微服务架构,它们都在试着将各种软、硬…...

【算法设计与分析】STL容器、递归算法、分治法、蛮力法、回溯法、分支限界法、贪心法、动态规划;各类算法代码汇总
文章目录前言一、STL容器二、递归算法三、分治法四、蛮力法五、回溯法六、分支限界法七、贪心法八、动态规划前言 本篇共为8类算法(STL容器、递归算法、分治法、蛮力法、回溯法、分支限界法、贪心法、动态规划),则各取每类算法中的几例经典示例进行展示。 一、STL容…...
vue初识
第一次接触vue,前端的html,css,jquery,js学习也有段时间了,就照着B站的视频简单看了一些,了解了一些简单的用法,这边做一个记录。 官网 工具:使用VSCode以及Live Server插件(能够实时预览) 第…...

火山引擎入选《2022 爱分析 · DataOps 厂商全景报告》,旗下 DataLeap 产品能力获认可
更多技术交流、求职机会,欢迎关注字节跳动数据平台微信公众号,回复【1】进入官方交流群 2 月 9 日,国内领先的数字化市场研究与咨询机构爱分析发布了《2022 爱分析DataOps 厂商全景报告》(以下简称报告),报…...

java-spring_bean的生命周期
生命周期:从创建到消亡的完整过程初始化容器 1. 创建对象(内存分配 ) 2. 执行构造方法 3. 执行属性注入(set操作) 4. 执行bean初始化方法 使用bean 执行业务操作 关闭/销毁容器 1.执行bean销毁方法 bean销毁时机 容…...
微服务相关概念
一、谈谈你对微服务的理解,微服务有哪些优缺点?微服务是由Martin Fowler大师提出的。微服务是一种架构风格,通过将大型的单体应用划分为比较小的服务单元,从而降低整个系统的复杂度。优点:1、服务部署更灵活࿱…...
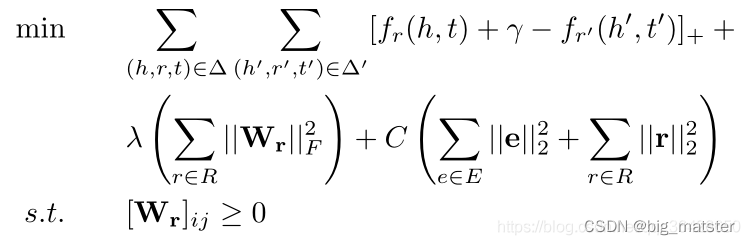
论文解读:(TransA)TransA: An Adaptive Approach for Knowledge Graph Embedding
简介 先前的知识表示方法:TransE、TransH、TransR、TransD、TranSparse等。的损失函数仅单纯的考虑hrh rhr和ttt在某个语义空间的欧氏距离,认为只要欧式距离最小,就认为h和th和th和t的关系为r。显然这种度量指标过于简单,虽然先…...

js将数字转十进制+十六进制(联动el-ui下拉选择框)
十进制与十六进制的整数转化一、十进制转十六进制二、十六进制转十进制三、联动demo一、十进制转十六进制 正则表达式: /^([0-9]||([1-9][0-9]{0,}))$/解析:[0-9]代表个位数,([1-9][0-9]{0,})代表十位及以上 二、十六进制转十进制 正则表达…...

关于RedissonLock的一些所思
关于RedissonClient.getLock() 我们一般的使用Redisson的方式就是: RLock myLock redissonClient.getLock("my_order");//myLock.lock();//myLock.tryLock();就上面的例子里,如果某个线程已经拿到了my_order的锁,那别的线程调用m…...

C++:倒牛奶问题
文章目录题目一、输入二、输出三、思路代码题目 农业,尤其是生产牛奶,是一个竞争激烈的行业。Farmer John发现如果他不在牛奶生产工艺上有所创新,他的乳制品生意可能就会受到重创! 幸运的是,Farmer John想出了一个好主…...
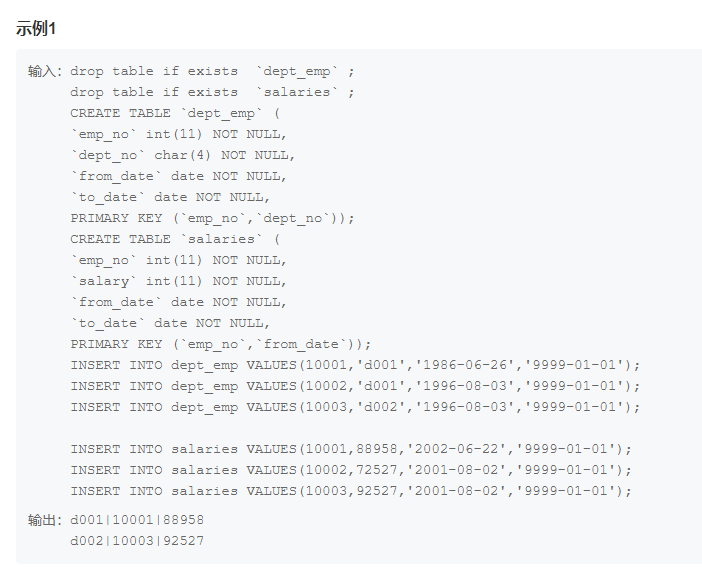
MySQL8.x group_by报错的4种解决方法
在我们使用MySQL的时候总是会遇到各种各样的报错,让人头痛不已。其中有一种报错,sql_modeonly_full_group_by,十分常见,每次都是老长的一串出现,然后带走你所有的好心情,如:LIMIT 0, 1000 Error…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

ThreadLocal 源码
ThreadLocal 源码 此类提供线程局部变量。这些变量不同于它们的普通对应物,因为每个访问一个线程局部变量的线程(通过其 get 或 set 方法)都有自己独立初始化的变量副本。ThreadLocal 实例通常是类中的私有静态字段,这些类希望将…...

DeepSeek越强,Kimi越慌?
被DeepSeek吊打的Kimi,还有多少人在用? 去年,月之暗面创始人杨植麟别提有多风光了。90后清华学霸,国产大模型六小虎之一,手握十几亿美金的融资。旗下的AI助手Kimi烧钱如流水,单月光是投流就花费2个亿。 疯…...

如何通过git命令查看项目连接的仓库地址?
要通过 Git 命令查看项目连接的仓库地址,您可以使用以下几种方法: 1. 查看所有远程仓库地址 使用 git remote -v 命令,它会显示项目中配置的所有远程仓库及其对应的 URL: git remote -v输出示例: origin https://…...

shell脚本质数判断
shell脚本质数判断 shell输入一个正整数,判断是否为质数(素数)shell求1-100内的质数shell求给定数组输出其中的质数 shell输入一个正整数,判断是否为质数(素数) 思路: 1:1 2:1 2 3:1 2 3 4:1 2 3 4 5:1 2 3 4 5-------> 3:2 4:2 3 5:2 3…...