计算机中有符号数的表示
文章目录
- 二进制数制
- 十进制
- 二进制
- 位模式
- 基本数据类型
- 无符号数的编码
- 有符号数的编码
- 原码(Sign-Magnitude)
- 反码(Ones' Complement)
- 补码(Two's Complement)
- 概念导读
- 编码格式
- 按权展开
- 补码加法
- 扩展一个数字的位表示
- 有符号数和无符号数之间的转换
- 参考
二进制数制
所谓数制是指计数的方法。
十进制
人两手加起来共10根手指,故日常计数和做算术都使用十进制。大家熟悉并使用了一千多年的十进制起源于印度,在12世纪被阿拉伯数学家改进,并在13世纪被意大利数学家Leonardo Pisano(Fibonacci)带到西方。1、2、3的罗马计数法是Ⅰ、Ⅱ、Ⅲ,Ⅰ+Ⅱ=Ⅲ 直观展示了加法运算的含义。
数据无论使用哪种进位制,都涉及两个基本要素:基数(radix)与各数位的“位权”(weight)。
十进制数有两个特点:
- 用0、1、2、3、…、9这10个基本符号表示;基本数字符号(数码)的个数叫基数。
- 遵循“逢十进一”原则,每位计满十时向高位进一。
一般地,任意一个十进制数 N 都可以表示为 ∑i=−mn−1Ki∗10i\sum_{i=-m}^{n-1}K_i\ast10^i∑i=−mn−1Ki∗10i:
N=Kn−1∗10n−1+Kn−2∗10n−2+⋯+K1∗101+K0∗100+K−1∗10−1+K−2∗10−2+⋯+K−m∗10−mN = K_{n-1}\ast10^{n-1} + K_{n-2}\ast10^{n-2} + \cdots + K_1\ast10^1 + K_0\ast10^0 + K_{-1}\ast10^{-1} + K_{-2}\ast10^{-2} + \cdots + K_{-m}\ast10^{-m} N=Kn−1∗10n−1+Kn−2∗10n−2+⋯+K1∗101+K0∗100+K−1∗10−1+K−2∗10−2+⋯+K−m∗10−m
抛开小数部分,整数按权的展开式为:
N=∑i=0n−1Ki∗10i=Kn−1∗10n−1+Kn−2∗10n−2+⋯+K1∗101+K0∗100N = \sum_{i=0}^{n-1}K_i\ast10^i = K_{n-1}\ast10^{n-1} + K_{n-2}\ast10^{n-2} + \cdots + K_1\ast10^1 + K_0\ast10^0 N=i=0∑n−1Ki∗10i=Kn−1∗10n−1+Kn−2∗10n−2+⋯+K1∗101+K0∗100
一个数字符号在不同位时,代表的数值不同。在上述表达式中,数位 KiK_iKi 的权为 10i10^i10i(以基数101010为底,序号iii为指数),数字符号乘以其位权为这个数字符号所表示的真实数值(Ki∗10iK_i\ast10^iKi∗10i)。
二进制
在 字节存储单元及struct内存分配 中,我们介绍了二进制和以及字节存储单元。现代计算机存储和处理的信息以二值信号表示。这些微不足道的二进制数字,或者称为位(bit),形成了数字革命的基础。
对于有10根手指的人来来说,使用十进制表示法是很自然的事情,但是当构造存储和处理信息的机器时,二进制工作得更好。在计算机内部,二进制总是存放在由具有两种相反状态的存储元件构成的寄存器或存储单元中,即二进制数码0和1是由存储元件的两种相反状态来表示的。这使得二值信号很容易地被表示、存储和传输。
二值信号可以表示为导线上的高电压或低电压、晶体管的导通或截止、电子自旋的两个方向,或者顺时针或逆时针的磁场。指令集及流水线 中提到,在上个世纪的打孔编程时代,纸带上的每个孔代表一位(bit),穿孔(presence)表示1,未穿孔(absence)表示0,这些孔序列被扫描识别为机器指令的二进制位串。
十进制数按权的展开式可以推广到任意进位计数制。二进制中只有0和1两个字符,基数为2,满足“逢二进一”。权用 2i2^i2i 表示,二进制的按权展开式为 N=∑i=0n−1Ki∗2iN = \sum_{i=0}^{n-1}K_i\ast2^iN=∑i=0n−1Ki∗2i。
二进制与其他数制相比,有以下显著特点:
- 数制简单,容易基于元器件的电子特性实现数字逻辑电路。
- 由于二进制只有状态,因此抗干扰性强,可靠性、稳定性高。
- 可以基于布尔逻辑代数进行分析和综合,运算规则相对简单易实现。
基数为2的好处在于基本算术运算表很短,对比一下十进制和二进制的加法和乘法表,长短相形一目了然。
位模式
2个比特可以组合出4(222^222)种状态,可表示无符号数值范围[0,3];32个比特可以组合出4294967296(2322^{32}232)种状态,可表示无符号数值范围[0,4294967295];……。
由于一个位只能表示二元数值,所以单独一位的用处不大。当把位组合在一起,再加上某种解释(interpretasion),即赋予不同的可能位模式以含意。通常将固定位数的位串作为一个基本存储单位,这样就可以存储范围较大的值。在有限范围内的可计量数值几乎都可以用二进制数码位串组合表示,计算机的内存由数以亿万计的比特位存储单元(晶体管)组成。
大多数计算机使用8位的块,或者字节(byte),作为最小的可寻址的内存单位,而不是访问内存中单独的位(bit)。机器级程序将内存视作一个非常大的字节数组,内存的每个字节都由一个唯一的数字来标识,称为它的地址。
每个程序对象可以简单地视为一个字节块,程序本身本身就是一个字节序列(机器指令序列)。
基本数据类型
在 C++ Variable Types 中,我们总结了C/C++中的基本数据类型。C/C++语言支持多种整形数据类型——表示有限范围的整数。每种类型都用关键字来指定大小,这些关键字包括 char、short、long,参考 gnu libc Integers。C/C++语言都支持有符号(默认)和无符号数。
- 长短修饰符
short和long用于修饰整形:默认为 long 长整形,短整形需显示指定 short。 - 符号修饰符
signed和unsigned用于修饰字符型和整形:缺省为signed有符号类型,无符号需显示指定unsigned修饰。 - 当用
signed/unsigned、short/long来修饰 int 整形时,int 可省略。
以下是字符型、短整型、整型有无符号的区分表示:
- 有符号字符型:char/signed char;无符号字符型:unsigned char
- 有符号短整型:short [int] /signed short [int];无符号短整型:unsigned short [int]
- 有符号整型:int /signed [int];无符号整型:unsigned [int]
无符号数的编码
无符号(unsigned)编码基于传统的二进制表示法,表示大于或等于0的非负数。
假设有一个整数数据类型有 nnn 位。我们可以将位向量写成 x⃗\vec{x}x 表示整个向量,或者写成 [xn−1,xn−2,⋯,x0][x_{n-1}, x_{n-2}, \cdots, x_0][xn−1,xn−2,⋯,x0],表示向量中的每一位。把 x⃗\vec{x}x 看成一个二进制表示的数,就获得了 x⃗\vec{x}x 的无符号表示。在这个二进制编码中,每个位 xix_ixi 都取值0或1,后一种取值意味着数值 2i2^i2i 应为数字值的一部分。我们用一个函数 B2UnB2U_nB2Un(Binary to Unsigned的缩写,长度为nnn)来表示。
对位向量 x⃗=[xn−1,xn−2,⋯,x0]\vec{x} = [x_{n-1}, x_{n-2}, \cdots, x_0]x=[xn−1,xn−2,⋯,x0]:
B2Un(x⃗)=˙∑i=0n−1xi∗2iB2U_n(\vec{x}) \dot=\sum_{i=0}^{n-1}x_i\ast2^i B2Un(x)=˙i=0∑n−1xi∗2i
在这个等式中,等号“=˙\dot==˙”表示左边被定义为等于右边。函数 B2UnB2U_nB2Un 将一个长度为 nnn 的0、1串映射到非负整数。
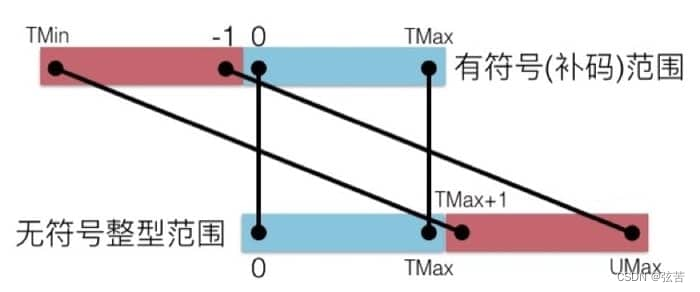
nnn 位所能表示的最小值用位向量[00⋯0][00\cdots0][00⋯0](全零)表示,也就是整数值0,而最大值是用位向量[11⋯1][11\cdots1][11⋯1](全1),也就是整数值 UMaxw=˙∑i=0n−1xi∗2i=2n−1UMax_w\dot=\sum_{i=0}^{n-1}x_i\ast2^i=2^n-1UMaxw=˙∑i=0n−1xi∗2i=2n−1。即nnn位二进制位串所能表示的数值范围是 [0,2n−1][0, 2^n-1][0,2n−1]。
在主流64位LP64架构实现中,unsigned char、unsigned short [int]、unsigned [int]、unsigned long [int](或 long unsigned [int])分别占1、2、4、8个字节(8、16、32、64位)。无符号字符(unsigned char)占用1个字节(8位),所能表示的数值范围是 [0,28−1]=[0,255][0, 2^8-1] = [0, 255][0,28−1]=[0,255]。
有符号数的编码
对于很多应用,我们还希望表示负数值。在计算机中,如何表示符号呢?
在计算机中,对于数的符号(正号+和负号-)也只能用0和1这两位数字表示。通常用一个数的最高位作为符号位,最高位为0表示符号位为正;最高位为1表示符号位为负。这样,数的符号标识也“数码化”了。即带符号数的数值和符号统一用二进制数码形式来表示。
在将数的符号用数码(0或1)表示后,数值部分究竟是保留原来的形式,还是按一定的规则做某些变化,这要取决于运算方法的需要,从而有四种常见的机器数形式:原码、反码、补码 和 移码。
为了区别原来的数与它在机器中的表示形式,将一个数(连同符号)在机器中加以数码化后的形式,称为机器数或机器码,而把机器数所代表的实际数值称为真值。
原码(Sign-Magnitude)
原码表示法比较直观,其数值部分保留其真值(的绝对值)。

- 8位二进制原码表示的数值范围为 11111111-10000000,00000000-01111111,即 -127 - -0,+0 - +127。其中,“0”有-0和+0之分,[−0]原=10000000[-0]_原=1 0000000[−0]原=10000000,[+0]原=00000000[+0]_原=0 0000000[+0]原=00000000。
例如,正数89的二进制表示为 +1011001+1011001+1011001,其原码表示为:

负数-89的二进制表示为 −1011001-1011001−1011001,其原码表示为:

原码表示法的优点是比较直观、简单易懂,后面在浮点数中有使用到原码编码。
原码的符号位不是数值的一部分,不能直接参与运算,导致加法运算复杂。
为了解决这些矛盾,人们引入了反码和补码。
反码(Ones’ Complement)
对于正数而言,其反码形式与其原码相同:最高位为符号位,用0表示正数,其余位为数值位不变。对于负数而言,其反码表示为:最高位符号位为1,其余数值位在原码的基础上按位取反。反码在机器中的表示形式如下:

- 8位二进制反码表示的数值范围为 10000000-11111111,00000000-01111111(负数数值部分求反复原:11111111-10000000,00000000-01111111),即 -127 - -0,+0 - +127。其中,“0”有-0和+0之分,[−0]反=11111111[-0]_反=1 1111111[−0]反=11111111,[+0]反=00000000[+0]_反=0 0000000[+0]反=00000000。
-89的二进制表示为 −1011001-1011001−1011001,其原码表示为 110110011 101100111011001,则其反码表示为 101001101 010011010100110。

将反码表示规则用表达式形式定义如下:
[X]反={X,X>0或X=+0(2n−1)−∣X∣((2n−1)+X),X<0或X=−0% 反码 [X]_反= \begin{cases} X, & X>0 或 X=+0 \\ (2^n-1)- \lvert X \rvert((2^n-1) + X), & X<0 或 X=-0 \end{cases} [X]反={X,(2n−1)−∣X∣((2n−1)+X),X>0或X=+0X<0或X=−0
当 X<0 或 X=-0 时,按照无符号数解析位向量,∣X∣+[X]反→=2n−1\lvert X \rvert + \overrightarrow{[X]_反}=2^n-1∣X∣+[X]反=2n−1。例如当n=8时,∣X∣+[X]反→=11111111=255\lvert X \rvert + \overrightarrow{[X]_反}=11111111=255∣X∣+[X]反=11111111=255。
虽然过去生产过基于反码表示的机器,但是几乎所有的现代机器都使用补码形式表示有符号整数。
现在通常已不再单独使用反码,而主要是作为求补码的一个中间步骤来使用。
补码(Two’s Complement)
在计算机中,最常见的有符号(整)数的表示方式是补码。采用补码运算可以将减法变成补码加法运算,在微处理器中只需加法的电路就可以实现加法、减法运算。
概念导读
为了理解补码的概念,我们先来看看圆周运动的例子。
在现实生活中,一个圆周的可视角度度量为0-2π(或0°-360°),以原点为起点的射线OA逆时针旋转一圈的弧度为2π。
圆周运动具有周期性,即具有“周而复始”的变化规律。假设OA的初始弧度为α,终边OA每绕原点旋转一周,α增加2π弧度(旋转k周后,弧度变成α+k·2π),但OA位置不变。由三角函数的定义可知,终边相同的角的同一三角函数的值相等。
sin(α+k⋅2π)=sinαcos(α+k⋅2π)=cosαtan(α+k⋅2π)=tanα\begin{gather*} \sin(\alpha+k·2\pi) = \sin\alpha \\ \cos(\alpha+k·2\pi) = \cos\alpha \\ \tan(\alpha+k·2\pi) = \tan\alpha \end{gather*} sin(α+k⋅2π)=sinαcos(α+k⋅2π)=cosαtan(α+k⋅2π)=tanα
由上面的公式可知,可以把求任意角的三角函数值,转化为求0-2π(或0°-360°)角的三角函数值。射线OA逆时针旋转π和顺时针旋转π(-π)的终边是相同的,逆时针旋转5π/3和顺时针旋转π/3(-π/3)的终边是相同的。以下将负弧度的正弦计算转化到0-2π区间换算:
sin(−π+2π)=sinπsin(−π3+2π)=sin5π3\begin{gather*} \sin(-\pi+2\pi) = \sin\pi \\ \sin(-\frac{\pi}{3}+2\pi) = \sin\frac{5\pi}{3} \end{gather*} sin(−π+2π)=sinπsin(−3π+2π)=sin35π
我们再来进一步看看日常生活中校正时钟的例子。
假定时钟停在7点,而正确时间是5点,要拨准时钟可以有两种不同的拨法:倒拨2个格或顺拨10个格。
想象一下,龟兔在7点钟刻度背向而行,假设兔子的速度是乌龟的5倍,兔子顺时针跑10格,乌龟逆时针跑2格,它们将在5点刻度处迎面相遇。
由于钟面的容量有限,其表盘刻度实际上是十二进制,12h以后又从0开始计数。倒拨2个格,即7-2=5(做减法);顺拨10个格,即7+10=12+5(做加法)。而钟面上12=0,故12+5回归到刻度5。这就表明,在舍掉进位的情况下,“从7减去2”和“往7加上10”所得的结果是一样的。在十二进制下,12+5丢失进位12,此处12是溢出量,又称为模(mod)。而2和10的和恰好等于模数12,我们把10称为-2对于模数12的补数。在圆周运动中,每转动一周的2π弧度可视为溢出量(模),5π/3为-π/3对于模数2π的补数。
在电脑和手机的日期和时间偏好设置中,通常可以设置显示24小时,因为地球自转一圈是一天(接近24h)。24h制的1点和13点都对应钟表上的1点。“天天向上”、“日复一日”中的“天”和“日”即为溢出量,每过24h(模)又将开启崭新的一天。
计算机中的运算受一定字长的限制,它的运算部件、寄存器和存储单元都有一定的位数,因而在运算过程中也会产生溢出量,所产生的溢出量实际上就是模。可见,计算机的运算也是一种有模运算。
编码格式
对于正数而言,其补码形式与其原码、反码相同:最高位为符号位,用0表示正数,其余位为数值位不变。对于负数而言,其补码表示为:最高位符号位为1,其余数值位在原码的基础上按位取反并加1(反码+1)。补码在机器中的表示形式如下:

-89的二进制表示为 −1011001-1011001−1011001,其原码表示为 110110011 101100111011001,其反码表示为 101001101 010011010100110,则其补码表示为 101001111 010011110100111。

- 8位二进制补码表示的数值范围为 10000000-11111111,00000000-01111111,即 -128 - -1,+0 - +127。其中,无-0和+0之分,保证了0的唯一性。另外,取值范围为连贯区间 [-128, 127],包含128个负数、128个非负数。负数、非负数各占一半,负数比正数多一个。
将补码表示规则用表达式形式定义如下:
[X]补={X,X≥02n−∣X∣(2n+X),X<0% 补码 [X]_补= \begin{cases} X, & X\ge0 \\ 2^n- \lvert X \rvert(2^n+X), & X<0 \end{cases} [X]补={X,2n−∣X∣(2n+X),X≥0X<0
当 X<0 时,按照无符号数解析位向量,∣X∣+[X]补→=2n\lvert X \rvert+\overrightarrow{[X]_补}=2^n∣X∣+[X]补=2n。例如当n=8时,∣X∣+[X]补→=11111111+1=256\lvert X \rvert+\overrightarrow{[X]_补}=11111111+1=256∣X∣+[X]补=11111111+1=256。
-89的二进制补码表示为 101001111 010011110100111,按照无符号数解析位向量的值为167,满足以下:
∣−89∣+167=256256+(−89)=167\begin{aligned} &\lvert -89 \rvert + 167 = 256 \\ & 256+(-89) = 167 \end{aligned} ∣−89∣+167=256256+(−89)=167
按权展开
-89的二进制表示为 −1011001-1011001−1011001,其原码表示为 110110011 101100111011001,其反码表示为 101001101 010011010100110,则其补码表示为 101001111 010011110100111。
∣−89∣\lvert -89 \rvert∣−89∣ 的二进制位向量为 010110010101100101011001:
- 反码数值部分位向量=(2n−1−1)−∣X∣=127−∣−89∣=0b01111111−0b01011001=0b00100110(2^{n-1}-1)-\lvert X \rvert = 127-\lvert -89 \rvert=0b01111111-0b01011001=0b00100110(2n−1−1)−∣X∣=127−∣−89∣=0b01111111−0b01011001=0b00100110。
- 补码数值部分位向量=(2n−1−1)−∣X∣+1=2n−1−∣X∣=127−∣−89∣+1=0b01111111−0b01011001+1=0b00100111(2^{n-1}-1)-\lvert X \rvert+1 = 2^{n-1}-\lvert X \rvert = 127-\lvert -89 \rvert+1=0b01111111-0b01011001+1=0b00100111(2n−1−1)−∣X∣+1=2n−1−∣X∣=127−∣−89∣+1=0b01111111−0b01011001+1=0b00100111。
补码高位符号位占1位,其余数值部分占 n-1 位。当将最高符号位解释为负权(2n−12^{n-1}2n−1)时,整体位向量刚好可计算出原始负值:
−2n−1+(2n−1−∣X∣)=−∣X∣-2^{n-1} + (2^{n-1}-\lvert X \rvert) = -\lvert X \rvert −2n−1+(2n−1−∣X∣)=−∣X∣
我们用一个函数 B2TwB2T_wB2Tw(Binary to Two’s Complement 的缩写,长度为www)来表示位向量 x⃗=[xn−1,xn−2,⋯,x0]\vec{x} = [x_{n-1}, x_{n-2}, \cdots, x_0]x=[xn−1,xn−2,⋯,x0] 到补码的编码映射:
B2Tn(x⃗)=˙−xn−1∗2n−1+∑i=0n−2xi∗2iB2T_n(\vec{x}) \dot=-x_{n-1}\ast2^{n-1} + \sum_{i=0}^{n-2}x_i\ast2^i B2Tn(x)=˙−xn−1∗2n−1+i=0∑n−2xi∗2i
最高有效位 xn−1x_{n-1}xn−1 称为符号位,它的“权重”为 −2n−1-2^{n-1}−2n−1,是无符号表示中权重的负数。符号位被设置为1时,表示值为负,而当设置为0时,值为非负。
∣−89∣\lvert -89 \rvert∣−89∣ 的二进制位向量为 010110010101100101011001,-89的二进制补码表示为 101001111 010011110100111,可基于 B2TnB2T_nB2Tn 函数按权展开复原补码的真值:
B2T8([01011001])=−0∗27+1∗26+1∗24+1∗23+1∗20=−0+64+16+8+1=89B2T8([10100111])=−1∗27+1∗25+1∗22+1∗21+1∗20=−128+32+4+2+1=−89\begin{aligned} & B2T_8([0 1011001]) = -0\ast2^7+1\ast2^6+1\ast2^4+1\ast2^3+1\ast2^0=-0+64+16+8+1=89 \\ & B2T_8([1 0100111]) = -1\ast2^7+1\ast2^5+1\ast2^2+1\ast2^1+1\ast2^0=-128+32+4+2+1=-89 \end{aligned} B2T8([01011001])=−0∗27+1∗26+1∗24+1∗23+1∗20=−0+64+16+8+1=89B2T8([10100111])=−1∗27+1∗25+1∗22+1∗21+1∗20=−128+32+4+2+1=−89
让我们基于 B2TnB2T_nB2Tn 展开式,重新推导一下 nnn 位补码所能表示的取值范围。
- 最小值是位向量 [10⋯0][10\cdots0][10⋯0],只设置负权,其他正权位清零,此种情形负得最多,其整数值为 TMinn=˙−2n−1TMin_{n}\dot=-2^{n-1}TMinn=˙−2n−1。
- 当设置了负权时,设置其他所有正权位,位向量为 [11⋯1][11\cdots1][11⋯1]。此种情形正权打满(负得最少),其整数值为 −2n−1+∑i=0n−2xi∗2i=−2n−1+(2n−1−1)=−1-2^{n-1}+\sum_{i=0}^{n-2}x_i\ast2^i=-2^{n-1}+(2^{n-1}-1)=-1−2n−1+∑i=0n−2xi∗2i=−2n−1+(2n−1−1)=−1,即最大负整数。
- 最大值是位向量 [01⋯1][01\cdots1][01⋯1],清除负权(即为非负数),清除其他所有正权位,其值为0;若设置其他所有正权位,其整数值为 TMaxn=˙∑i=0n−2xi∗2i=2n−1−1TMax_{n}\dot=\sum_{i=0}^{n-2}x_i\ast2^i=2^{n-1}-1TMaxn=˙∑i=0n−2xi∗2i=2n−1−1。
以n=8n=8n=8为例,一个字节(byte)的补码编码所能表示数值范围是 [−28−1,28−1−1][-2^{8-1}, 2^{8-1}-1][−28−1,28−1−1],即 [−128,127][-128, 127][−128,127],包含128个负数(-128 - -1)、128个非负数(0 - 127)。
补码加法
计算机的表示法使用有限数量的位对一个数字编码,当结果太大以至不能表示时,某些运算就会溢出(overflow)。因此,我们说计算机运算也是一种有模运算。当然,在计算机中不是像上述时钟例子那样以12为模,在定点小数的补码表示中是以 222 为模,在定点整数中则以 2n2^n2n 为模(n=8,16,32,64,…)。
计算机中用补码表示法编码有符号数,把负数用补码表示。减去一个正数可以看成加上一个负数,这样在计算机中不用单独设置减法器,而是基于补码一律按加法运算规则实现减法的等效计算。
回想调拨钟表的例子,2和10的和恰好等于模数12,我们把10称为-2对于mod12的补数。其含义是在钟表盘上,逆时针回拨2格等效于顺时针拨动10格。
【例1】已知X=+0000111(7),Y=-0010011(-19),求两数的补码之和。
- [X]补=00000111,[Y]补=11101101[X]_补=0 0000111,[Y]_补=1 1101101[X]补=00000111,[Y]补=11101101,人工计算 Z=X+Y=7+(-19)=-12(补码为11110100)。
若将 [Y]补→\overrightarrow{[Y]_补}[Y]补 也视作无符号数=237,将计算结果Z也直视为无符号数[Z]补→\overrightarrow{[Z]_补}[Z]补=244,满足 7+237=244。244恰为-12对于mod256的补数。
设想一个有256个刻度的大笨钟,初始在刻度7点处,逆时针回拨19格和顺时针拨动237格,效果都是拨到刻度244处。当采用补码表示时,表盘的256个刻度被重新编码,划分成左边逆时针半盘[-128,-1]和右边顺时针半盘[0,127],原先的244点映射为新刻度下左半盘的-12点位。换个角度来看,由于 ∣−19∣>∣7∣\lvert -19 \rvert \gt \lvert 7 \rvert∣−19∣>∣7∣,这里的异号相加,负数占主导,也可以想象初始刻度左半盘-19点,+7表示顺时针拨动7格,将拨到-12点,仍然在左半盘(没有溢出)。
在钟表盘刻度范围内,逆时针的减法和顺时针的加法(加减量互补),最终达到同一刻度点。在模数(例如mod256)范围内,减法可以视作加补码(计算反码本身已经做了减法运算),补码可以视作无符号数直接参与竖式按位加计算。另一方面,由于操作数和运算结果都统一用补码表示,补码的最高符号位统一按照负权解释,即补码的符号位可视作整体数值的一部分。从这个角度讲,符号位直接参与运算貌似也是解释得通。
接下来,我们重点看看补码加法的溢出问题及溢出判断。
【例2】已知X=+1000000(64),Y=+1000001(65),求两数的补码之和。
- 直接对补码列竖式计算如下:
01(CfC0)[X]补01000000(+64的补码)+)[Y]补01000001(+65的补码)10000001129\begin{array}{c|lcr} \:\:\:\:\: & \: \quad 0\ 1 \qquad\qquad\qquad (C_fC_0)\\ \:\:\:\:\: [X]_补 & \qquad 0\ 1000000 \qquad (+64的补码) \\ +) [Y]_补 & \qquad 0\ 1000001 \qquad (+65的补码) \\ \hline \ & \qquad 1\ 0000001 \qquad 129 \end{array} [X]补+)[Y]补 0 1(CfC0)0 1000000(+64的补码)0 1000001(+65的补码)1 0000001129
- 两个正数相加,结果为负数!?补码之和是129,超出了 [0, 127],即产生了溢出现象。此时,数值部分向符号位产生进位C0=1C_0=1C0=1,符号位未向高位产生进位 Cf=0C_f=0Cf=0。
这里两个正数相加,结果超出了8位补码的非负数表示范围,溢出到了负数区。还是借用256大笨钟来阐述,初始在刻度65点处,顺时针拨动64格,将到129点。但是,当采用补码表示时,129点越过右半盘(取值范围为[0,127])的分界线127点两格,落入了左半盘(取值范围为[-128,-1])的-127点位:+127左溢一格是-128,再左溢一格是-127。
用以下C语言代码测试验证,计算结果Z的位向量为0x81(即无符号数129),补码对应的真值=-127。
signed char X = 64;signed char Y = 65;signed char Z = X+Y;printf("Z=0x%hhx, %hhd\n", Z, Z);
【例3】已知X=-1111111(-127),Y=-0000010(-2),要求进行补码的加法运算。
- 直接对补码列竖式计算如下:
10(CfC0)[X]补10000001(−127的补码)+)[Y]补11111110(−2的补码:254)01111111127\begin{array}{c|lcr} \:\:\:\:\: & \: \quad 1\ 0 \qquad\qquad\qquad (C_fC_0)\\ \:\:\:\:\: [X]_补 & \qquad 1\ 0000001 \qquad (-127的补码) \\ +) [Y]_补 & \qquad 1\ 1111110 \qquad (-2的补码:254) \\ \hline \ & \qquad 0\ 1111111 \qquad 127 \end{array} [X]补+)[Y]补 1 0(CfC0)1 0000001(−127的补码)1 1111110(−2的补码:254)0 1111111127
- 两个负数相加,结果为正数!?预期的结果-129超出了8位补码所能表示的负数范围 [-128, -1],即产生了溢出现象。此时,数值部分向符号位未产生进位 C0=0C_0=0C0=0,符号位向高位产生进位 Cf=1C_f=1Cf=1。
这里两个负数相加,结果超出了8位补码的负数表示范围,溢出到了正数区。由于 ∣−127∣>∣−2∣\lvert -127 \rvert \gt \lvert -2 \rvert∣−127∣>∣−2∣,这里的负负相加,-127占主导。还是借用256大笨钟来阐述,当采用补码表示时,想象初始刻度左半盘-127点处,-2表示逆时针拨动2格,越过左半盘分界线-128点一格,落入了右半盘(取值范围为[0,127])的127点位:-127右溢一格是-128,再右溢一格是+127。
用以下C语言代码测试验证,计算结果Z的位向量为0x7f,符号位溢出为0,补码对应的真值即无符号值127。
signed char X = -127;signed char Y = -2;signed char Z = X+Y;printf("Z=0x%hhx, %hhd\n", Z, Z);
【例4】已知X=-0000011(-3),Y=-0000010(-2),要求进行补码的加法运算。
- 直接对补码列竖式计算如下:
11(CfC0)[X]补11111101(−3的补码:253)+)[Y]补11111110(−2的补码:254)11111011(−5的补码:251)\begin{array}{c|lcr} \:\:\:\:\: & \: \quad 1\ 1 \qquad\qquad\qquad (C_fC_0)\\ \:\:\:\:\: [X]_补 & \qquad 1\ 1111101 \qquad (-3的补码:253) \\ +) [Y]_补 & \qquad 1\ 1111110 \qquad (-2的补码:254) \\ \hline \ & \qquad 1\ 1111011 \qquad (-5的补码:251) \end{array} [X]补+)[Y]补 1 1(CfC0)1 1111101(−3的补码:253)1 1111110(−2的补码:254)1 1111011(−5的补码:251)
- 直接补码运算产生的结果的无符号数值是251,正是预期结果-5的补码!此时,数值部分向符号位产生进位 C0=1C_0=1C0=1,符号位向高位产生进位 Cf=1C_f=1Cf=1,未溢出。
以上例1和例4中,8位正数之和、8位负数之和未超出8位补码表示的数值范围时,没有产生溢出,结果正确。此时,满足 C0=CfC_0=C_fC0=Cf,同时为0或同时为1。
以上例2和例3中,8位正数之和、8位负数之和超出8位补码表示的数值范围时,产生了溢出,结果错误。此时,满足 C0≠CfC_0 \ne C_fC0=Cf,一个为0且一个为1。
综合以上,可用下列逻辑表达式进行补码加法的溢出判断:
OF=Cf⊕C0OF = C_f \oplus C_0 OF=Cf⊕C0
扩展一个数字的位表示
一个常见的运算是在不同字长的整数之间转换,同时又保持数值不变。考虑从一个较小的数据类型转换到一个较大的类型,即扩大位宽。
要将一个无符号数转换成一个更大的数据类型时,只要简单地在开头添加0。具体来说,原数值的字节保持在低(权)位不变,在新增的高(权)位补0。
要将一个补码数字转换为一个更大的数据类型,可以执行一个符号扩展(sign extension)。具体来说,原数值的字节保持在低(权)位不变,在新增的高(权)位复制符号位。
- 对于正数,高位复制符号位0,不影响其真值。
- 对于负数,高位复制符号位1,也不影响真值。
考虑负数的补码位向量 x⃗=[xw−1,xw−2,⋯,x0]\vec{x} = [x_{w-1}, x_{w-2}, \cdots, x_0]x=[xw−1,xw−2,⋯,x0],其编码映射如下:
B2Tw(x⃗)=˙−xw−1∗2w−1+∑i=0w−2xi∗2iB2T_w(\vec{x}) \dot=-x_{w-1}\ast2^{w-1} + \sum_{i=0}^{w-2}x_i\ast2^i B2Tw(x)=˙−xw−1∗2w−1+i=0∑w−2xi∗2i
当复制高符号位 xw−1x_{w-1}xw−1 时,位向量 x′⃗=[xw−1,⋯,xw−1,xw−1,xw−2,⋯,x0]\vec{x'} = [x_{w-1}, \cdots, x_{w-1}, x_{w-1}, x_{w-2}, \cdots, x_0]x′=[xw−1,⋯,xw−1,xw−1,xw−2,⋯,x0],则有 B2Tw(x⃗)=B2Tw′(x′⃗)B2T_w(\vec{x}) = B2T_{w'}(\vec{x'})B2Tw(x)=B2Tw′(x′)。
以-89为例,其8位补码位向量为[10100111][1 0100111][10100111],将其符号扩展为16位的位向量位[1111111110100111][11111111 10100111][1111111110100111]:
B2T8([10100111])=−1∗27+1∗25+1∗22+1∗21+1∗20=−128+32+4+2+1=−89B2T16([1111111110100111])=−1∗215+1∗214+⋯+1∗28+1∗27+1∗25+1∗22+1∗21+1∗20=−128+32+4+2+1=−89\begin{aligned} & B2T_8([1 0100111]) = -1\ast2^7+1\ast2^5+1\ast2^2+1\ast2^1+1\ast2^0=-128+32+4+2+1=-89 \\ & B2T_{16}([11111111 10100111]) =-1\ast2^{15}+1\ast2^{14}+\cdots+1\ast2^8+1\ast2^7+1\ast2^5+1\ast2^2+1\ast2^1+1\ast2^0=-128+32+4+2+1=-89 \end{aligned} B2T8([10100111])=−1∗27+1∗25+1∗22+1∗21+1∗20=−128+32+4+2+1=−89B2T16([1111111110100111])=−1∗215+1∗214+⋯+1∗28+1∗27+1∗25+1∗22+1∗21+1∗20=−128+32+4+2+1=−89
我们设补码除符号位后的数值位值为v,则
B2T8([10100111])=−1∗27+vB2T16([1111111110100111])=−1∗215+1∗214+⋯+1∗28+1∗27+v\begin{aligned} & B2T_8([1 0100111]) =-1\ast2^7+v \\ & B2T_{16}([11111111 10100111]) =-1\ast2^{15}+1\ast2^{14}+\cdots+1\ast2^8+1\ast2^7+v \end{aligned} B2T8([10100111])=−1∗27+vB2T16([1111111110100111])=−1∗215+1∗214+⋯+1∗28+1∗27+v
更进一步有:
B2T16([1111111110100111])=28(−27+26+⋯+20)+27+v=28(−27+(27−1))+27+v=−28+27+v=−27+v\begin{aligned} B2T_{16}([11111111 10100111]) & = 2^8(-2^7+2^6+\cdots+2^0)+2^7+v \\ & = 2^8(-2^7+(2^7-1))+2^7+v \\ & = -2^8+2^7+v \\ & = -2^7+v \end{aligned} B2T16([1111111110100111])=28(−27+26+⋯+20)+27+v=28(−27+(27−1))+27+v=−28+27+v=−27+v
对比可知,符号扩展前后的补码所表示的真值不变。
有符号数和无符号数之间的转换
C语言允许在各种不同的数据类型之间做强制类型转换。例如,假设变量x声明为int,u声明为unsigned。表达式 (unsigned)x 会将x的值转换为一个无符号数值,而 (int)u 将u的值转换为一个有符号整数。
考虑以下代码:
short int v = -12345;unsigned short uv = (unsigned short)v;printf("v=%hd, uv=%hu\n", v, uv);printf("v=0x%hx, uv=0x%hx\n", v, uv);
在一台采用补码的机器上,上述代码运行输出:
v=-12345, uv=53191
v=0xcfc7, uv=0xcfc7
可以看到,强制类型转换的结果保持位向量(位模组)不变,只是改变了解释这些位的方式。
v=-12345 的补码表示和 uv=53191 的无符号表示是完全一样的。
以上代码片段示例演示了负数补码转换成无符号数。对于负数,补码中最高位作为符号位,本来解释为负权 −2w−1-2^{w-1}−2w−1,按照无符号解释为正权数值位 2w−12^{w-1}2w−1。由于后面位的数值 vvv 保持不变,相当于在补码表示的真值基础上加上 2w2^w2w。
对满足 TMinw≤x≤TMaxwTMin_w \le x \le TMax_wTMinw≤x≤TMaxw 的 xxx 有:
T2Uw(x)={x,x≥02w+x(2w−∣x∣),x<0T2U_w(x)= \begin{cases} x, & x\ge0 \\ 2^w+x(2^w- \lvert x \rvert), & x<0 \end{cases} T2Uw(x)={x,2w+x(2w−∣x∣),x≥0x<0
简单推导如下:
B2Uw(x)−B2Tw(x)=(2w−1+v)−(−2w−1+v)=2∗2w−1=2w⟹B2Uw(x)=B2Tw(x)+2w\begin{aligned} B2U_w(x) - B2T_w(x) & = (2^{w-1}+v)-(-2^{w-1}+v) = 2\ast2^{w-1}=2^w \\ & \implies B2U_w(x) = B2T_w(x) + 2^w \end{aligned} B2Uw(x)−B2Tw(x)=(2w−1+v)−(−2w−1+v)=2∗2w−1=2w⟹B2Uw(x)=B2Tw(x)+2w
例如:T2U16(−12345)=−12345+216=53191T2U_{16}(-12345) = -12345+2^{16}=53191T2U16(−12345)=−12345+216=53191。
同理,无符号数的最高位解释为正权数值位 2w−12^{w-1}2w−1,当将其位向量解释成补码时,最高位将作为符号位,解释为负权 −2w−1-2^{w-1}−2w−1。由于后面位的数值 vvv 保持不变,相当于在无符号真值基础上减去 2w2^w2w。
对满足 0≤u≤UMaxw0 \le u \le UMax_w0≤u≤UMaxw 的 uuu 有:
U2Tw(u)={u,u≤TMaxwu−2w,u>TMaxwU2T_w(u)= \begin{cases} u, & u \le TMax_w \\ u - 2^w, & u>TMax_w \end{cases} U2Tw(u)={u,u−2w,u≤TMaxwu>TMaxw
对于 w=8w=8w=8,当 u≤TMaxw=127u \le TMax_w = 127u≤TMaxw=127 时,即 0≤u≤1270 \le u \le 1270≤u≤127,刚好落入8位补码所能表示的非负数区间 ;当 u>TMaxw=127u \gt TMax_w = 127u>TMaxw=127 时,例如 128≤u≤255128 \le u \le 255128≤u≤255,则原始高位1变成负号,补码释义为负数。原来位向量按无符号解释出的真值需减去 28=2562^8=25628=256,换算出按补码解释的正确真值,对应负数区间 [−1,−128][-1, -128][−1,−128]。
我们在数轴上把有符号数和无符号数画出来的话,就能很清晰的看出相对的关系:
参考
《深入理解计算机系统》(第3版)
《计算机组成原理》(第3版),唐朔飞
《微机原理与接口技术》(第2版),王克义
《汇编语言程序设计》(第4版),文全刚
深入谈谈二进制
补码表示法的本质原理
【读薄 CSAPP】壹 数据表示
从晶体管开始聊聊计算机为什么采用二进制
相关文章:

计算机中有符号数的表示
文章目录二进制数制十进制二进制位模式基本数据类型无符号数的编码有符号数的编码原码(Sign-Magnitude)反码(Ones Complement)补码(Twos Complement)概念导读编码格式按权展开补码加法扩展一个数字的位表示…...
MySQL(一)服务器连接 库的基本操作
目录 一、连接服务器 二、简单使用 三、校验规则 条件筛选 where 进行order排序 三、查看数据库 使用 show databases;(注意分号和最后一个s) 显示创建数据库的详情信息:使用show create database test2; 四、修改数据库 五…...
Maven怎样构建生命周期?
项目构建生命周期Maven的本质是一个项目管理工具,将项目开发和管理过程抽象成一个项目对象模型(POM)。Maven构建生命周期描述的是一次构建过程经历经历了多少个事件。对项目构建的生命周期划分为3套,其中clean负责清理工作,default负责核心工…...
真实3D地形生成器【免费在线】
Terrain3D是一个免费的在线3D地形生成器,只需指定地球上的坐标,就可以自动生成附近区域的3D地形同时叠加卫星影像,并且可以导出GLTF格式的3D地形模型。 推荐:使用 NSDT场景设计器 快速搭建 3D场景。 使用Terrain3D生成真实世界的3…...
)
华为OD机试 - 整数编码(Python)
整数编码 题目 实现一个整数编码方法 使得待编码的数字越小 编码后所占用的字节数越小 编码规则如下 编码时7位一组,每个字节的低 7 位用于存储待编码数字的补码字节的最高位表示后续是否还有字节,置1表示后面还有更多的字节,置0表示当前字节为最后一个字节采用小端序编码…...

【GlobalMapper精品教程】051:融合Dissolve操作详解
本节讲解globalmapper中融合Dissolve工具的使用。 文章目录 一、工具介绍1. 工具位置2. 融合工具二、案例实战1. 加载实验数据2. 根据字段分组融合案例一:根据地类名称分组,将相同的类型融合到一起。案例二:根据权属地类名称分组,将相同的类型融合到一起。一、工具介绍 1.…...

Java Excel的数据导入导出
引入依赖 <!-- EasyExcel --> <dependency><groupId>com.alibaba</groupId><artifactId>easyexcel</artifactId><version>2.2.7</version> </dependency><!--csv文件操作--> <dependency><groupId>n…...
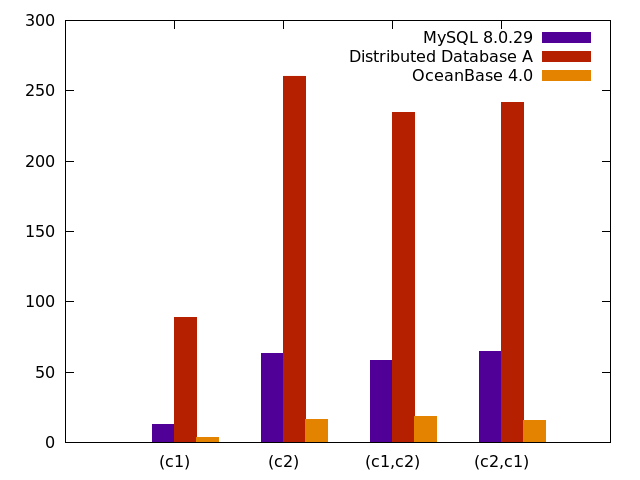
OceanBase 4.0解读:兼顾高效与透明,我们对DDL的设计与思考
关于作者 谢振江,OceanBase 高级技术专家。 2015年加入 OceanBase, 从事存储引擎相关工作,目前在存储-索引与 DDL 组,负责索引,DDL 和 IO 资源调度相关工作。 回顾关系型数据库大规模应用以来的发展,从单机到分布式无…...

Qt线程池
目录1、线程池是什么?2、Qt线程池2.1、用法例程2.2、线程池对性能的提升2.3、运行算法单线程写法线程池写法1、线程池是什么? 线程池是一种线程使用模式,它管理着一组可重用的线程,可以处理分配过来的可并发执行的任务。 线程池设…...

设置table中的tbody
<!DOCTYPE html> <html> <head> <meta charset"utf-8"> <title>设置table中的tbody</title> </head> <body> <script> // 这里有json数据,是jav…...
2023美赛A题完整数据!思路代码数据数学建模
选取内蒙古河套灌区(典型干旱区)2010-2020年气温,降雨,蒸散发和水汽压月数据 包括四种主要作物及其占比 内容截图如下: 链接为:https://www.jdmm.cc/file/2708703 同时还提供参考代码和参考文章的选项~…...
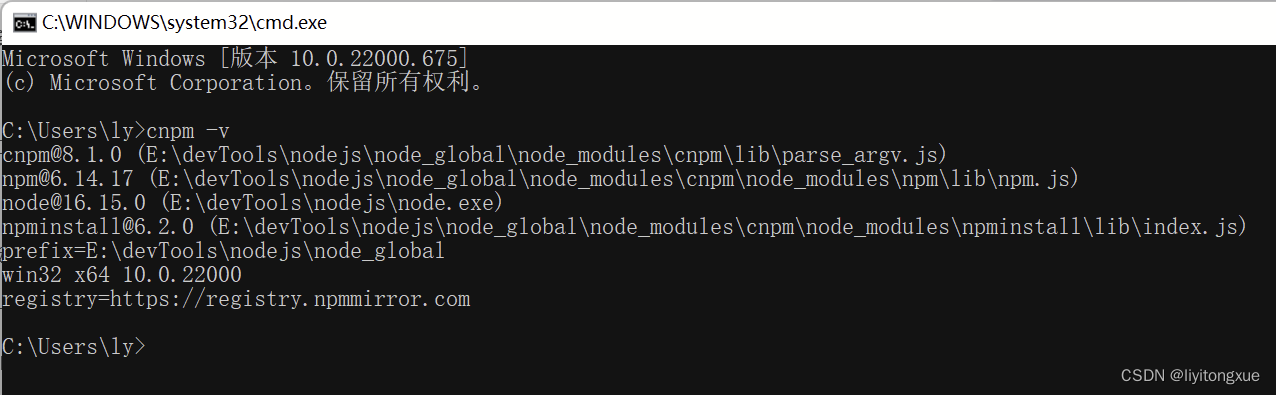
Node.js安装与配置
Node.js安装与配置 前言 本篇博文记录了Node.js安装与环境变量配置的详细步骤,旨在为将来再次配置Node.js时提供指导方法。 另外:Node.js版本请根据自身系统选择,安装位置、全局模块存放位置和环境变量应根据自身实际情况进行更改。 Node…...
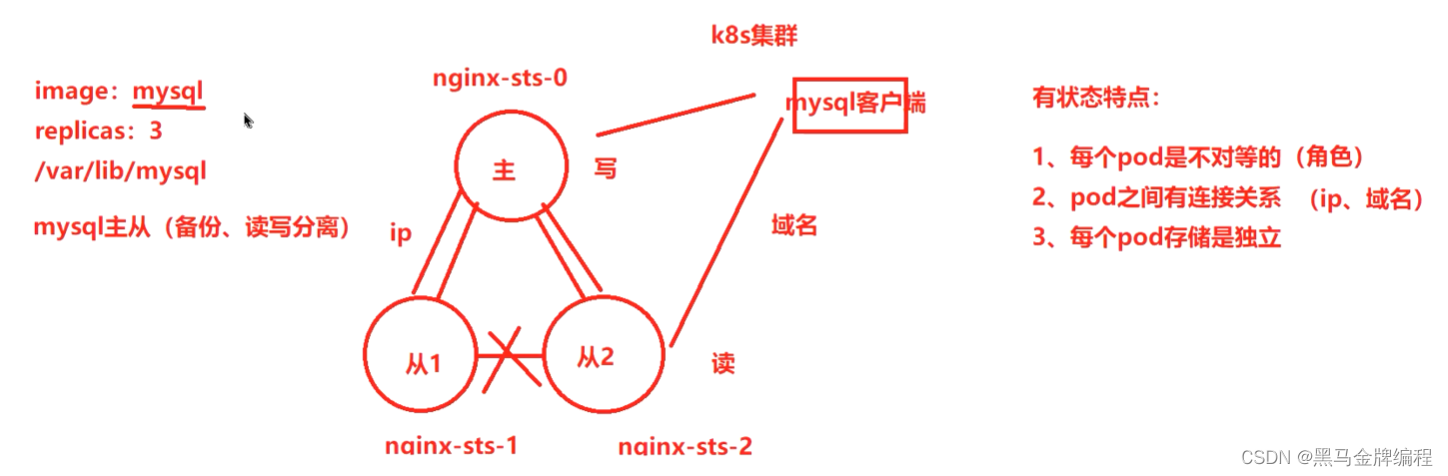
k8s(存储)数据卷与数据持久卷
为什么需要数据卷? 容器中的文件在磁盘上是临时存放的,这给容器中运行比较重要的应用程序带来一些问题问题1:当容器升级或者崩溃时,kubelet会重建容器,容器内文件会丢失问题2:一个Pod中运行多个容器并需要共…...
php5.6.9安装sqlsrv扩展(windows)
报错:Marning: PHP Startup: Unable to load dynamic 1library D:lphpstudy_prolExtensionslphpl(phps.6.9ntslextphp_ pdo_sqlsry 56 nts′找不到指定的模块。in Unknown on line 0 整整搞了一天才终于解决 我用的是phpstudy_pro(也就是小皮v8.1版本)&…...
参数检查 cookie黑名单 POST参数检查参考代码)
URL黑名单 扫描工具ua特征 GET(args)参数检查 cookie黑名单 POST参数检查参考代码
资源宝分享www.httple.net 文章目录URL黑名单扫描工具ua特征GET(args)参数检查cookie黑名单POST参数检查注:请先检查是否已设置URL白名单,若已设置URL白名单,URL黑名单设置将失效 多个URL配置需换行,一行只允许填写一个。可直接填…...

【软考系统架构设计师】2022下论文写作历年真题
【软考系统架构设计师】2022下论文写作历年真题 试题四 论湖仓一体架构及其应用(75分) 试题四 论湖仓一体架构及其应用 随着5G、大数据、人工智能、物联网等技术的不断成熟,各行各业的业务场景日益复杂,企业数据呈现出大规模、多…...

推荐3个好用的scrum敏捷项目管理工具
结合对工具的了解和使用心得,介绍在管理scrum中常见的一些工具基础的scrum工具:1、物理白板物理白板是实施scrum最简单直接的方式。之前我也说过,一些利弊。数据不能够沉淀等等。2、Excel表格表格的形式就是如果多人编辑时,不能实…...

每日学术速递2.17
CV - 计算机视觉 | ML - 机器学习 | RL - 强化学习 | NLP 自然语言处理 Subjects: cs.LG 1.Decoupled Model Schedule for Deep Learning Training 标题:深度学习训练的解耦模型时间表 作者:Hongzheng Chen, Cody Hao Yu, Shuai Zheng, Zhen Zhang,…...
ElementUI`resetFields()`方法避坑
使用ElementUI中的resetFields()方法有哪些注意点 场景一 场景一:当编辑弹出框和新增弹出框共用时,编辑数据后关闭编辑弹出框时调用this.$refs.form.resetFields()无法清空弹出框 问题代码: // 点击新增按钮handleAdd() {this.dialogVi…...
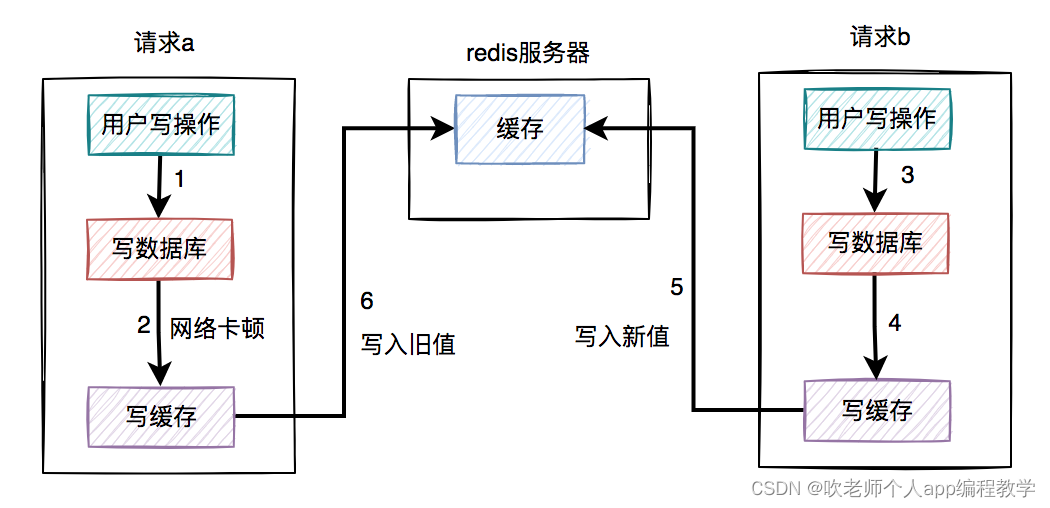
如何保证数据库和缓存双写一致性?
前言 数据库和缓存(比如:redis)双写数据一致性问题,是一个跟开发语言无关的公共问题。尤其在高并发的场景下,这个问题变得更加严重。 我很负责的告诉大家,该问题无论在面试,还是工作中遇到的概率…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...
