「计算机组成原理」数据的表示和运算(上)
文章目录
- 一、进位计数制
- 1.1 其他进制转十进制
- 1.2 十进制转其他进制
- 1.3 二进制、八进制和十六进制
- 1.3 真值和机器数
- 二、BCD码
- 2.1 8421码
- 2.2 余3码
- 2.3 2421码
- 三、整数的表示和运算
- 3.1 无符号整数
- 3.1.1 无符号整数的表示
- 3.1.2 无符号整数的运算
- 3.2 有符号整数
- 3.2.1 有符号整数的表示
- 3.2.2 有符号整数的补码运算
- 四、定点小数的表示和运算
一、进位计数制
不同的进制,每一位的位权不一样。如数字KnKn−1...K2K1K0.K−1K−2...K−mK_{n}K_{n-1}...K_{2}K_{1}K_{0}.K_{-1}K_{-2}...K_{-m}KnKn−1...K2K1K0.K−1K−2...K−m,以小数点为分界线,小数点以前的n+1位数字的位权从右到左依次是r0,r1,...,rn−1r^{0},r^{1},...,r^{n-1}r0,r1,...,rn−1;小数点以后的m位数字的位权从左至右依次是r−1,r−2,...,r−mr^{-1},r^{-2},...,r^{-m}r−1,r−2,...,r−m.其中r是该数字的基数:不同进制的基数不同,十进制每一位可能出现的字符是0~9共10个,则十进制的基数是10;二进制每一位可能出现的字符是0或1,则二进制的基数是2.
1.1 其他进制转十进制
任意进制要想转换为十进制,只需要将该数字的每一位与本位的位权相乘,再将结果相加即可。
二进制转为十进制:101.1=1×22+0×21+1×20+1×2−1=5.5101.1 = 1\times2^{2}+0\times2^{1}+1\times2^{0}+1\times2^{-1}=5.5101.1=1×22+0×21+1×20+1×2−1=5.5
八进制转为十进制:5.4=5×80+4×8−1=5.55.4 = 5\times8^{0}+4\times8^{-1}=5.55.4=5×80+4×8−1=5.5
十六进制转为十进制:5.8=5×160+8×16−1=5.55.8=5\times16^{0}+8\times16^{-1}=5.55.8=5×160+8×16−1=5.5
1.2 十进制转其他进制
十进制转换为其他进制要分为小数点前后的整数部分和小数部分。对于整数部分使用除基取余的方法,先取得“余”是整数的低位;对于小数部分使用乘基取整的方法,先取的“整”是小数的高位。
对于任意的r进制数字要转换为十进制:KnKn−1...K2K1K0.K−1K−2...K−m=Kn×rn+Kn−1×rn−1+...+K2×r2+K1×r1+K0×r0+K−1×r−1+K−2×r−2+...+K−m×r−mK_{n}K_{n-1}...K_{2}K_{1}K_{0}.K_{-1}K_{-2}...K_{-m}=K_{n}\times r^{n}+K_{n-1}\times r^{n-1}+...+K_{2}\times r^{2}+K_{1}\times r^{1}+K_{0}\times r^{0}+K_{-1}\times r^{-1}+K_{-2}\times r^{-2}+...+K_{-m}\times r^{-m}KnKn−1...K2K1K0.K−1K−2...K−m=Kn×rn+Kn−1×rn−1+...+K2×r2+K1×r1+K0×r0+K−1×r−1+K−2×r−2+...+K−m×r−m.
其整数部分若除以基数即Kn×rn+Kn−1×rn−1+...+K2×r2+K1×r1+K0×r0r=Kn×rn−1+Kn−1×rn−2+...+K2×r1+K1×r0......K0\frac{K_{n}\times r^{n}+K_{n-1}\times r^{n-1}+...+K_{2}\times r^{2}+K_{1}\times r^{1}+K_{0}\times r^{0}}{r}=K_{n}\times r^{n-1}+K_{n-1}\times r^{n-2}+...+K_{2}\times r^{1}+K_{1}\times r^{0}......K_{0}rKn×rn+Kn−1×rn−1+...+K2×r2+K1×r1+K0×r0=Kn×rn−1+Kn−1×rn−2+...+K2×r1+K1×r0......K0,其中K0K_{0}K0为余数,其余的为商,并且K0<rK_{0}<rK0<r,不难看出K0K_{0}K0就是该r进制数整数部分的最低位,将商继续除以基数r就可以依次获得高位。
其小数部分若乘以基数即K−1×r−1+K−2×r−2+...+K−m×r−m×r=K−1×r0+K−2×r−1+...+K−m×r−m+1K_{-1}\times r^{-1}+K_{-2}\times r^{-2}+...+K_{-m}\times r^{-m} \times r=K_{-1}\times r^{0}+K_{-2}\times r^{-1}+...+K_{-m}\times r^{-m+1}K−1×r−1+K−2×r−2+...+K−m×r−m×r=K−1×r0+K−2×r−1+...+K−m×r−m+1,由于r是大于1的,则r的负指数必然小于1,因此该结果的整数部分为K−1K_{-1}K−1,这样就得到了小数部分的第一位,以此类推可以得到更低的几位。
这里需要注意的是,十进制转换为其他进制的时候,想要得到目标进制整数部分的时候需要除法操作取余数,每次的被除数是上一次的商,这样算下去一定会算到商为0,此时整数部分的计算也就完成了。而小数部分需要进行乘法操作,每次都要用小数部分与基数相乘取积的整数部分,直到积为0为止,但是有时候我们永远都无法乘到0如0.3转换为二进制,几次乘法之后会发现开始了循环导致永远也乘不到严格的0,这也就导致了小数部分不精确,因此十进制可能无法严格转换为其他进制。
十进制转换为二进制:75.3
整数部分:752=37...1\frac{75}{2}=37...1275=37...1
372=18...1\frac{37}{2}=18...1237=18...1
182=09...0\frac{18}{2}=09...0218=09...0
092=04...1\frac{09}{2}=04...1209=04...1
042=02...0\frac{04}{2}=02...0204=02...0
022=01...0\frac{02}{2}=01...0202=01...0
012=00...1\frac{01}{2}=00...1201=00...1
整数部分结果为1001011
小数部分:0.3×2=0.6=0+0.60.3\times2=0.6=0+0.60.3×2=0.6=0+0.6
0.6×2=1.2=1+0.20.6\times2=1.2=1+0.20.6×2=1.2=1+0.2
0.2×2=0.4=0+0.40.2\times2=0.4=0+0.40.2×2=0.4=0+0.4
0.4×2=0.8=0+0.80.4\times2=0.8=0+0.80.4×2=0.8=0+0.8
0.8×2=1.6=1+0.60.8\times2=1.6=1+0.60.8×2=1.6=1+0.6
..................
小数部分结果为011001…
则75.3转换为二进制为1001011.01001…
1.3 二进制、八进制和十六进制
二进制与八进制和十六进制可以快速转换。三位二进制可以组成一位八进制;四位二进制可以组成一位十六进制。若二进制位数不够,小数点前需高位补0;小数点后需低位补0.
二进制 —> 八进制:1111000010.011010 —> 001 111 000 010 . 011 010 —> 1702.32
二进制 —> 十六进制:1111000010.01101000 —> 0011 1100 0010 . 0110 1000 —> 3C2.68
八进制 —> 二进制:251.5O —> 010 101 001 . 101
十六进制 —> 二进制:AE86.1H —> 1010 1110 1000 0110 . 0001
1.3 真值和机器数
真值就是我们平常习惯使用的十进制数字,机器数就是这些我们惯用的十进制数字在计算机中存储的二进制形式,正负号在机器数中是需要被数字化的,0代表整数,1代表负数。
真值 机器数
+15 0 1111
-08 1 1000
二、BCD码
BCD(Binary-Coded Decimal)码就是用二进制编码的十进制,他分为3种,分别是8421码、余3码和2421码。其中8421码和2421码为有权码,余3码为无权码。这三种编码方式都是用4位二进制数字表示1位十进制,只不过映射方式不同。
2.1 8421码
8421码与十进制的映射关系如下:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 |
0101+1000=1101,显然1101这个编码无法对应任何一个十进制数字。这个时候需要把非法结果+0110修正为合法结果。上述结果1101+0110=1 0011,再将高位补全得到0001 0011,这样就可以和表中一一对应。
此处的修正方法为计算机需要使用的方法,我们平常计算的时候可以直接用十进制算出结果,然后将每一个十进制位对应到8421编码即可。之所以+110即6是因为8421码从1010开始就无法对应十进制位,此时真值为10,再加上6便可以向前进位而保留低位。
2.2 余3码
余3码就是在8421码的基础上,每一个编码+0011,其与十进制映射关系如下:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 |
2.3 2421码
2421码每一位的权值由高到低依次是2、4、2、1,其与十进制映射关系如下:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 0000 | 0001 | 0010 | 0011 | 0100 | 1011 | 1100 | 1101 | 1110 | 1111 |
在2421码中,规定0~4的编码以0开头,5~9的编码以1开头。若不遵守这个规定,则此编码会有歧义。如十进制的5,按照2421的权值来看,可以有0101和1011两种编码方式,这显然是不应该出现的。
三、整数的表示和运算
3.1 无符号整数
3.1.1 无符号整数的表示
无符号整数的表示有如下特征:
- 所有二进制位都是数值位,没有符号位
- 第i位的位权是2i−12^{i-1}2i−1
- n bit无符号整数可表示的范围是0~2n−10~2^{n}-10~2n−1,超过这个范围则会发生溢出
- 可以表示的最小数字是全0,可以表示的最大数字是全1
3.1.2 无符号整数的运算
无符号整数的加法运算只需要从最低位开始,按位相加,向高处进位。而无符号整数的减法运算
需要先将减法转换为加法,然后按照加法规则相加即可。这样做一方面是因为加法运算的电路简单且成本低,另一方面可以让计算机用同样的方法处理运算,计算机擅长做重复的事情。
如A-B需要将其转化为等价的加法形式A+(-B),此处的-B不是前者B的相反数,而是通过将减数B全部位按位取反,末位+1这个规则得到的。
A:99 —> 01100011
B:09 —> 00001001
计算A-B,先将“B”转换为“-B”:00001001 (按位取反)—> 11110110 (末位+1)—> 11110111
0 1 1 0 0 0 1 1
+1 1 1 1 0 1 1 1
————————
1 0 1 0 1 1 0 1 0 = 90
舍去高位的1bit,得到结果01011010即90
3.2 有符号整数
3.2.1 有符号整数的表示
有符号数可以用原码、反码、补码和移码表示,其中移码只能表示整数。原码就是通过真值直接转换为二进制所得到的,只不过最高位是符号位,且符号位不能参与运算。用原码进行计算不方便,而补码可以很方便地进行运算,所以实际运算用的都是补码。
正数的原反补码是一样的。
负数的反码需要将其原码的数值位按位取反,符号位保持不变,负数的补码需要在其反码的末位+1,这个过程同样适用于补码转原码。虽然负数的原反补码是通过变化得来的,但是它们的最高位即符号位不会发生变化,都能够正确的表示正负。
对于负数来说,有一种快捷的从原码转变为补码的方式:从右往左找到第一个“1”,将这个“1”左边的所有数值位按位取反,符号位不变,就可以直接得到该原码的补码。同样也可以由此方法将补码转换为原码。
| n+1 bit | 合法表示范围 | 最大的数 | 最小的数 | 真值0的表示 |
|---|---|---|---|---|
| 带符号整数:原码 | −(2n−1)⩽x⩽2n−1-(2^{n}-1)\leqslant x\leqslant 2^{n}-1−(2n−1)⩽x⩽2n−1 | 0,111...111=2n−10,111...111= 2^{n}-10,111...111=2n−1 | 1,111...111=−(2n−1)1,111...111= -(2^{n}-1)1,111...111=−(2n−1) | [+0]原=0,000...000[+0]_{原}=0,000...000[+0]原=0,000...000 [−0]原=1,000...000[-0]_{原}=1,000...000[−0]原=1,000...000 |
| 带符号整数:反码 | −(2n−1)⩽x⩽2n−1-(2^{n}-1)\leqslant x\leqslant 2^{n}-1−(2n−1)⩽x⩽2n−1 | 0,111...111=2n−10,111...111= 2^{n}-10,111...111=2n−1 | 1,111...111=−(2n−1)1,111...111= -(2^{n}-1)1,111...111=−(2n−1) | [+0]反=0,000...000[+0]_{反}=0,000...000[+0]反=0,000...000 [−0]反=1,111...111[-0]_{反}=1,111...111[−0]反=1,111...111 |
| 带符号整数:补码 | −2n⩽x⩽2n−1-2^{n}\leqslant x\leqslant 2^{n}-1−2n⩽x⩽2n−1 | 0,111...111=2n−10,111...111= 2^{n}-10,111...111=2n−1 | 1,000...000=−2n1,000...000= -2^{n}1,000...000=−2n | [0]补=0,000...000[0]_{补}=0,000...000[0]补=0,000...000 真值0只有一种补码 |
| 带符号整数:移码 | −2n⩽x⩽2n−1-2^{n}\leqslant x\leqslant 2^{n}-1−2n⩽x⩽2n−1 | 1,111...111=2n−11,111...111= 2^{n}-11,111...111=2n−1 | 0,000...000=−2n0,000...000= -2^{n}0,000...000=−2n | [0]移=1,000...000[0]_{移}=1,000...000[0]移=1,000...000 真值0只有一种移码 |
| 无符号整数 | 0⩽x⩽2n+1−10\leqslant x\leqslant 2^{n+1}-10⩽x⩽2n+1−1 | 1111...111=2n+1−11111...111= 2^{n+1}-11111...111=2n+1−1 | 0000...000=00000...000= 00000...000=0 | [0]移=1,000...000[0]_{移}=1,000...000[0]移=1,000...000 |
原码和反码的合法表示范围完全相同,真值0都有2种形式;
补码和移码的合法表示范围完全相同,比原码多表示一个负数,真值0只有1种形式。
8bit的机器数,用不同的方式解读的结果如图所示。可以看出移码和无符号数的机器数的绝对值越大,其真值就越大。

不同码之间的转化如图所示:

3.2.2 有符号整数的补码运算
补码的加法运算按位相加即可,向高位进位,符号位参与运算。
A:+19 —> 0,0010011 (原码)
B: -19 —> 1,0010011 (原码)
计算A+B:
直接使用原码运算:
0 0 0 1 0 0 1 1
+1 0 0 1 0 0 1 1
————————
1 0 1 0 0 1 1 0 = 166
显然这个结果是错误的。
A:+19 —> 0,0010011 (原码) —> 0,0010011(补码)
B: -19 —> 1,0010011 (原码) —> 1,1101101(补码)
使用补码运算:
0 0 0 1 0 0 1 1
+1 1 1 0 1 1 0 1
————————
1 0 0 0 0 0 0 0 0 = 0
最高位溢出,保留低8位,得到了正确的结果0。
和无符号整数的减法一样,补码的减法运算也需要将减法转换为等价的加法,也就是将减数B的补码转换为-B的补码。转换规则和无符号整数B转换为-B的方法一样,将[B]补[B]_{补}[B]补全部位按位取反后+1,即可得到[−B]补[-B]_{补}[−B]补。
从[B]补[B]_{补}[B]补转换到[−B]补[-B]_{补}[−B]补也有一种简单的算法:找到[B]补[B]_{补}[B]补最右边的“1”,将这个“1”左边的全部位按位取反即可得到[−B]补[-B]_{补}[−B]补。(注意与前边负数的原码补码转换方法区别)
A:+19 —> 0,0010011(原码) —> 0,0010011(补码)
B: -19 —> 1,0010011(原码) —> 1,1101101(补码)
计算A-B,首先转换为A+(-B)
[−B]补=00010011[-B]_{补}=00010011[−B]补=00010011
计算A+(-B):
0 0 0 1 0 0 1 1
+0 0 0 1 0 0 1 1
————————
0 0 1 0 0 1 1 0 = 38
四、定点小数的表示和运算
定点整数可以用原码、反码、补码和移码表示,定点小数可以用原反补码表示而不能用移码表示。
定点是指小数点的位置固定不变。在定点整数中,我们默认小数点在最低位的后边;在定点小数中,我们默认小数点在符号位和数值最高位之间。因此若需要位数扩展时,两者的扩展位置是不一样的:定点整数在高位扩展,定点小数在低位扩展。
定点小数三种码之间的转换和定点整数三种码之间的转换是完全一致的,运算方法也与定点整数完全一致:加减法需要先转换为补码,减法要先转换为加法,这个转换也和定点整数是一样的。
| n+1 bit | 合法表示范围 | 最大的数 | 最小的数 | 真值0的表示 |
|---|---|---|---|---|
| 定点整数:原码 | −(2n−1)⩽x⩽2n−1-(2^{n}-1)\leqslant x\leqslant 2^{n}-1−(2n−1)⩽x⩽2n−1 | 0,111...111=2n−10,111...111= 2^{n}-10,111...111=2n−1 | 1,111...111=−(2n−1)1,111...111= -(2^{n}-1)1,111...111=−(2n−1) | [+0]原=0,000...000[+0]_{原}=0,000...000[+0]原=0,000...000 [−0]原=1,000...000[-0]_{原}=1,000...000[−0]原=1,000...000 |
| 定点整数:反码 | −(2n−1)⩽x⩽2n−1-(2^{n}-1)\leqslant x\leqslant 2^{n}-1−(2n−1)⩽x⩽2n−1 | 0,111...111=2n−10,111...111= 2^{n}-10,111...111=2n−1 | 1,111...111=−(2n−1)1,111...111= -(2^{n}-1)1,111...111=−(2n−1) | [+0]反=0,000...000[+0]_{反}=0,000...000[+0]反=0,000...000 [−0]反=1,111...111[-0]_{反}=1,111...111[−0]反=1,111...111 |
| 定点整数:补码 | −2n⩽x⩽2n−1-2^{n}\leqslant x\leqslant 2^{n}-1−2n⩽x⩽2n−1 | 0,111...111=2n−10,111...111= 2^{n}-10,111...111=2n−1 | 1,000...000=−2n1,000...000= -2^{n}1,000...000=−2n | [0]补=0,000...000[0]_{补}=0,000...000[0]补=0,000...000 真值0只有一种补码 |
| 定点小数:原码 | −(1−2−n)⩽x⩽1−2−n-(1-2^{-n})\leqslant x\leqslant 1-2^{-n}−(1−2−n)⩽x⩽1−2−n | 0.111...111=1−2−n0.111...111= 1-2^{-n}0.111...111=1−2−n | 1.111...111=−(1−2−n)1.111...111= -(1-2^{-n})1.111...111=−(1−2−n) | [+0]原=0.000...000[+0]_{原}=0.000...000[+0]原=0.000...000 [−0]原=1.000...000[-0]_{原}=1.000...000[−0]原=1.000...000 |
| 定点小数:反码 | −(1−2−n)⩽x⩽1−2−n-(1-2^{-n})\leqslant x\leqslant 1-2^{-n}−(1−2−n)⩽x⩽1−2−n | 0.111...111=1−2−n0.111...111= 1-2^{-n}0.111...111=1−2−n | 1.111...111=−(1−2−n)1.111...111= -(1-2^{-n})1.111...111=−(1−2−n) | [+0]反=0.000...000[+0]_{反}=0.000...000[+0]反=0.000...000 [−0]反=1.111...111[-0]_{反}=1.111...111[−0]反=1.111...111 |
| 定点小数:补码 | −1⩽x⩽1−2−n-1\leqslant x\leqslant 1-2^{-n}−1⩽x⩽1−2−n | 0.111...111=1−2−n0.111...111= 1-2^{-n}0.111...111=1−2−n | 1.000...000=−11.000...000= -11.000...000=−1 | [0]补=0,000...000[0]_{补}=0,000...000[0]补=0,000...000 真值0只有一种补码 |
相关文章:

「计算机组成原理」数据的表示和运算(上)
文章目录一、进位计数制1.1 其他进制转十进制1.2 十进制转其他进制1.3 二进制、八进制和十六进制1.3 真值和机器数二、BCD码2.1 8421码2.2 余3码2.3 2421码三、整数的表示和运算3.1 无符号整数3.1.1 无符号整数的表示3.1.2 无符号整数的运算3.2 有符号整数3.2.1 有符号整数的表…...

分层,均质,稀薄燃烧
均质燃烧: 只能使用火花点燃。 即为普通燃烧方式,燃料和空气混合形成一定浓度的可燃混合气(厂家自配),整个燃烧室内混合气的空燃比是相同的,经火花塞点燃燃烧。这种燃烧方式使燃料和空气充分混合,燃料完全燃烧,从而获得大的输出功率。为使混合…...
)
mybatis-plus小课堂:多表查询【案例篇】(apply 拼接 in SQL,来查询从表某个范围内的数据)
文章目录 引言I 多表查询1.1 多表查询:在mapper.xml 写语句和拼接查询条件1.2 多表关联:Java代码中书写语句和拼接查询条件1.3 案例:左外连接II mybatis-Plus 之 apply 拼接 in SQL2.1 apply源码实现2.2 apply 拼接 in SQLIII 常见问题3.1 Cause: comColumn xxx in where cl…...
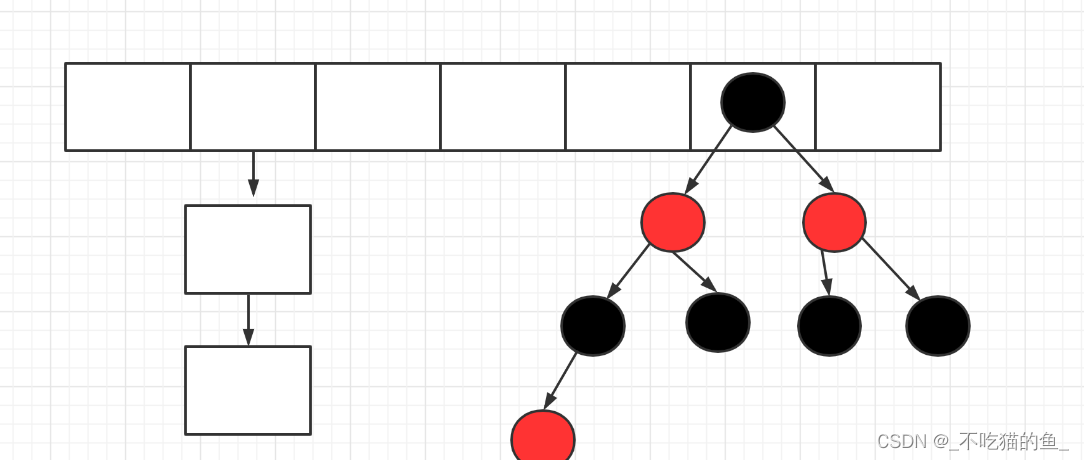
HashMap原理详解
一、hashmap简介 hashmap是Java当中一种数据结构,是一个用于存储Key-Value键值对的集合,每一个键值对也叫作Entry。 二、JDK7的HashMap1、JDK7时HashMap的数据结构 1、在JDK7之前,hashmap底层采用数组链表的数据结构来存储数据 2、插入数据采…...
推荐3款远程办公软件
一款好用的远程办公软件能够大大的提高我们的办公效率,在这篇文章中,我们将为您推荐几款常见又好用的远程办公软件,以帮助您能更加高效的远程办公。电脑远程办公软件有很多,本文主要从团队沟通软件、视频会议软件、远程控制软件等…...
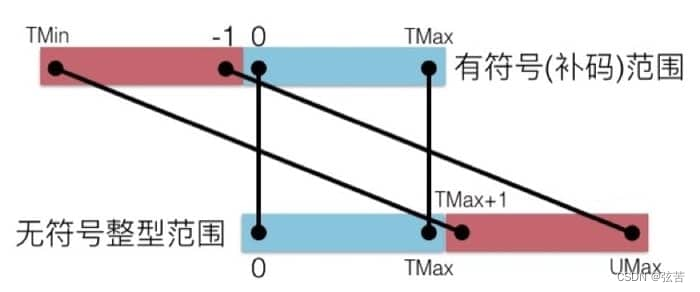
计算机中有符号数的表示
文章目录二进制数制十进制二进制位模式基本数据类型无符号数的编码有符号数的编码原码(Sign-Magnitude)反码(Ones Complement)补码(Twos Complement)概念导读编码格式按权展开补码加法扩展一个数字的位表示…...
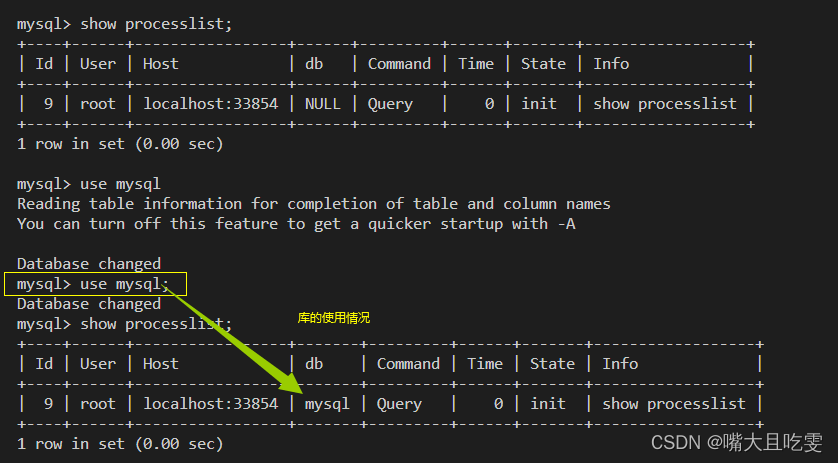
MySQL(一)服务器连接 库的基本操作
目录 一、连接服务器 二、简单使用 三、校验规则 条件筛选 where 进行order排序 三、查看数据库 使用 show databases;(注意分号和最后一个s) 显示创建数据库的详情信息:使用show create database test2; 四、修改数据库 五…...
Maven怎样构建生命周期?
项目构建生命周期Maven的本质是一个项目管理工具,将项目开发和管理过程抽象成一个项目对象模型(POM)。Maven构建生命周期描述的是一次构建过程经历经历了多少个事件。对项目构建的生命周期划分为3套,其中clean负责清理工作,default负责核心工…...
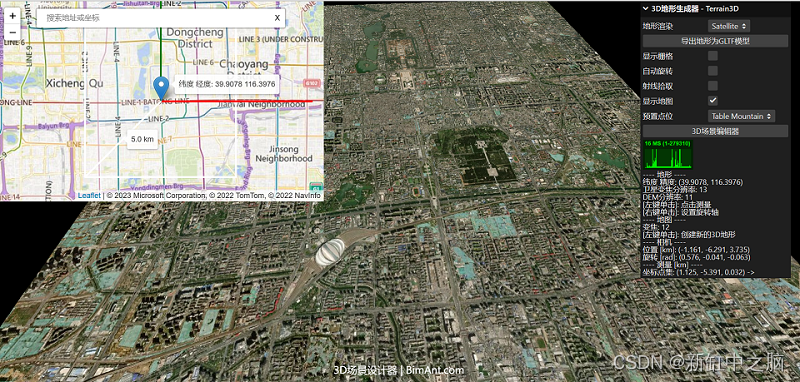
真实3D地形生成器【免费在线】
Terrain3D是一个免费的在线3D地形生成器,只需指定地球上的坐标,就可以自动生成附近区域的3D地形同时叠加卫星影像,并且可以导出GLTF格式的3D地形模型。 推荐:使用 NSDT场景设计器 快速搭建 3D场景。 使用Terrain3D生成真实世界的3…...
)
华为OD机试 - 整数编码(Python)
整数编码 题目 实现一个整数编码方法 使得待编码的数字越小 编码后所占用的字节数越小 编码规则如下 编码时7位一组,每个字节的低 7 位用于存储待编码数字的补码字节的最高位表示后续是否还有字节,置1表示后面还有更多的字节,置0表示当前字节为最后一个字节采用小端序编码…...

【GlobalMapper精品教程】051:融合Dissolve操作详解
本节讲解globalmapper中融合Dissolve工具的使用。 文章目录 一、工具介绍1. 工具位置2. 融合工具二、案例实战1. 加载实验数据2. 根据字段分组融合案例一:根据地类名称分组,将相同的类型融合到一起。案例二:根据权属地类名称分组,将相同的类型融合到一起。一、工具介绍 1.…...

Java Excel的数据导入导出
引入依赖 <!-- EasyExcel --> <dependency><groupId>com.alibaba</groupId><artifactId>easyexcel</artifactId><version>2.2.7</version> </dependency><!--csv文件操作--> <dependency><groupId>n…...
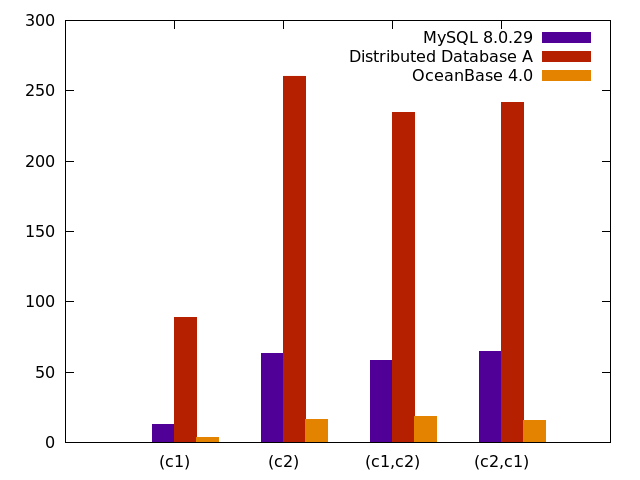
OceanBase 4.0解读:兼顾高效与透明,我们对DDL的设计与思考
关于作者 谢振江,OceanBase 高级技术专家。 2015年加入 OceanBase, 从事存储引擎相关工作,目前在存储-索引与 DDL 组,负责索引,DDL 和 IO 资源调度相关工作。 回顾关系型数据库大规模应用以来的发展,从单机到分布式无…...

Qt线程池
目录1、线程池是什么?2、Qt线程池2.1、用法例程2.2、线程池对性能的提升2.3、运行算法单线程写法线程池写法1、线程池是什么? 线程池是一种线程使用模式,它管理着一组可重用的线程,可以处理分配过来的可并发执行的任务。 线程池设…...

设置table中的tbody
<!DOCTYPE html> <html> <head> <meta charset"utf-8"> <title>设置table中的tbody</title> </head> <body> <script> // 这里有json数据,是jav…...
2023美赛A题完整数据!思路代码数据数学建模
选取内蒙古河套灌区(典型干旱区)2010-2020年气温,降雨,蒸散发和水汽压月数据 包括四种主要作物及其占比 内容截图如下: 链接为:https://www.jdmm.cc/file/2708703 同时还提供参考代码和参考文章的选项~…...
Node.js安装与配置
Node.js安装与配置 前言 本篇博文记录了Node.js安装与环境变量配置的详细步骤,旨在为将来再次配置Node.js时提供指导方法。 另外:Node.js版本请根据自身系统选择,安装位置、全局模块存放位置和环境变量应根据自身实际情况进行更改。 Node…...
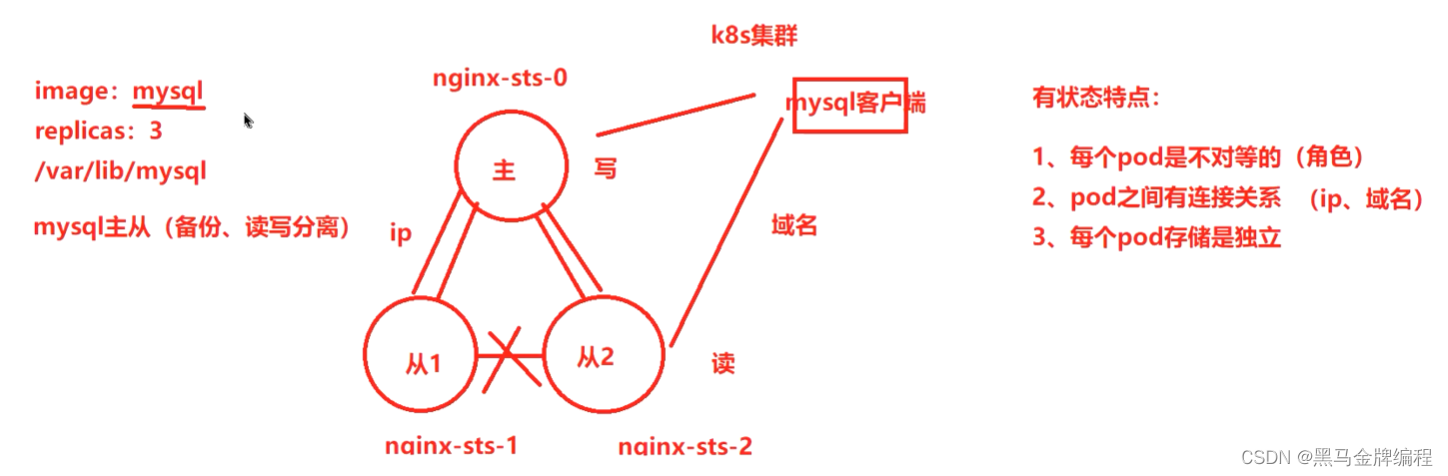
k8s(存储)数据卷与数据持久卷
为什么需要数据卷? 容器中的文件在磁盘上是临时存放的,这给容器中运行比较重要的应用程序带来一些问题问题1:当容器升级或者崩溃时,kubelet会重建容器,容器内文件会丢失问题2:一个Pod中运行多个容器并需要共…...
php5.6.9安装sqlsrv扩展(windows)
报错:Marning: PHP Startup: Unable to load dynamic 1library D:lphpstudy_prolExtensionslphpl(phps.6.9ntslextphp_ pdo_sqlsry 56 nts′找不到指定的模块。in Unknown on line 0 整整搞了一天才终于解决 我用的是phpstudy_pro(也就是小皮v8.1版本)&…...
参数检查 cookie黑名单 POST参数检查参考代码)
URL黑名单 扫描工具ua特征 GET(args)参数检查 cookie黑名单 POST参数检查参考代码
资源宝分享www.httple.net 文章目录URL黑名单扫描工具ua特征GET(args)参数检查cookie黑名单POST参数检查注:请先检查是否已设置URL白名单,若已设置URL白名单,URL黑名单设置将失效 多个URL配置需换行,一行只允许填写一个。可直接填…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...
