LA@生成子空间@范数@衡量矩阵大小@正交化
文章目录
- 线性组合与线性方程组
- 生成子空间
- 范数
- LpL^pLp范数
- 向量点积用范数表示
- ref
- 衡量矩阵大小
- 特殊类型矩阵和向量
- 对角阵
- 向量长度
- 性质
- 单位向量
- 向量单位化(正规化)
- 正交
- 向量正交
- 正交向量组
- 标准正交基
- 正交化(schmidt)
- 正交矩阵
- 矩阵是正交矩阵的充要条件
- 对称矩阵
- 正交相似
- 概念区分🎈
- 正交相似对角化
- 实对称方阵A正交对角化方法
线性组合与线性方程组
-
如果A是方阵,其逆矩阵 A−1A^{−1}A−1 存在,那么式 Ax=bAx=bAx=b 肯定对于每一个向量 bbb 恰好存在一个解。
-
但是,对于一般的方程组而言(A不一定是方阵),对于向量 b 的某些值,有可能不存在解,或者存在无限多个解两,或者存在唯一解。
-
存在多于一个解(是少2个)但是少于无限多个解(解的数量有限而不是无穷大)的情况是不可能发生的;
-
因为如果 x 和y 都是某方程组的解(Ax=b,Ay=b)Ax=b,Ay=b)Ax=b,Ay=b),则
-
z=αx+βy,其中α+β=1z=\alpha{x}+\beta{y},其中\alpha+\beta=1 z=αx+βy,其中α+β=1
-
对于任意α∈R\alpha\in{R}α∈R,zzz肯定也是Ax=bAx=bAx=b的解,因为:
-
Az=αAx+βAy=αb+βb=(α+β)b=bAz=\alpha{A}x+\beta{A}y=\alpha{b}+\beta{b}=(\alpha+\beta)b=b Az=αAx+βAy=αb+βb=(α+β)b=b
-
-
-
-
为了分析方程有多少个解,我们可以将 A 的列向量看作从 原点(origin)(元素都是零的向量,对于n维向量,可以理解为n维点,例如三维空间原点(0,0,0))出发的不同方向(用AAA的一个列向量来对应表示一个方向),确定有多少种方法可以到达向量 bbb。
-
设A∈Rm×nA\in\mathbb{R}^{m\times{n}}A∈Rm×n,则x∈Rnx\in\mathbb{R}^{n}x∈Rn,也即是说A可以看成由n个列向量构成的矩阵(用αi\alpha_iαi表示第i个方向)
-
A=(α1,α2,⋯,αn)A=(\alpha_1,\alpha_2,\cdots,\alpha_n)A=(α1,α2,⋯,αn)
-
x=(x1x2⋮xn)x=\begin{pmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \\ \end{pmatrix} x=x1x2⋮xn
-
-
解向量 xxx 中的每个元素xix_ixi表示应该沿着方向αi\alpha_iαi走多的距离为 xix_ixi
-
将这些步骤效果叠加:
-
Ax=∑i=1nαixi=bAx=\sum\limits_{i=1}^{n}\alpha_{i}x_i=b Ax=i=1∑nαixi=b
-
这种操作称为向量组的线性组合(向量bbb用矩阵A的列向量组线性表出,表出系数为向量xxx)
- 其中αi\alpha_iαi是向量,xix_ixi是标量
-
而Ax=bAx=bAx=b的线性方程组展开
-
是从矩阵乘积的结果bbb(或解向量xxx)的逐个分量的角度描述.
-
Ax=∑i=1mβix=b{a11x1+a12x2+⋯+a1nxn=b1,a21x1+a22x2+⋯+a2nxn=b2,⋮am1x1+am2x2+⋯+amnxn=bnAx=\sum\limits_{i=1}^{m}\beta_{i}x=b\\ \left \{\begin{aligned}{} a_{11} x_{1}+a_{12} x_{2}+\cdots+a_{1 n} x_{n}&=b_{1}, \\ a_{21} x_{1}+a_{22} x_{2}+\cdots+a_{2 n} x_{n}&=b_{2}, \\ \vdots&\\ a_{m1} x_{1}+a_{m 2} x_{2}+\cdots+a_{m n} x_{n}&=b_{n} \end{aligned} \right. Ax=i=1∑mβix=b⎩⎨⎧a11x1+a12x2+⋯+a1nxna21x1+a22x2+⋯+a2nxn⋮am1x1+am2x2+⋯+amnxn=b1,=b2,=bn
- 其中βi\beta_iβi是矩阵A的第i个行向量(分块),xxx是解向量
-
-
-
生成子空间
-
一组向量的 生成子空间(span)是原始向量线性组合后所能抵达的结果的集合。
-
确定 Ax=bAx = bAx=b 是否有解相当于确定向量 b 是否在 A 列向量的生成子空间中。
- A∈Rm×nA\in\mathbb{R}^{m\times{n}}A∈Rm×n
- x∈Rn×1x\in\mathbb{R}^{n\times{1}}x∈Rn×1
- b∈Rm×1b\in\R^{m\times{1}}b∈Rm×1
-
A向量组的生成子空间被称为 A 的 列空间(column space)或者 A 的 值域(range)。
-
为了使方程 Ax=bAx = bAx=b 对于任意向量 b∈Rmb\in\mathbb{R}^mb∈Rm 都存在解,我们要求 A 的列空间构成整个 Rm\mathbb{R}^mRm。
- 这意味者b一定会落在A的列空间
-
如果 Rm\mathbb{R}^mRm 中的某个点不在 A 的列空间中(向量b无法被矩阵A线性表出),那么该点对应的 b 会使得该方程没有解。
-
矩阵 A 的列空间是整个 Rm\mathbb{R}^mRm 的要求,意味着 A 至少有 m 列,即
- n⩾mn\geqslant mn⩾m。否则,A 列空间的维数会小于 m。
- 例如,假设 A 是一个 3 × 2 的矩阵。目标 b 是 3 维的,但是 x 只有 2 维。
- 所以无论如何修改二维向量 xxx 的值,也只能描绘出 R3\mathbb{R}^3R3 空间中的二维平面,当且仅当向量 b 在该二维平面中时,该方程有解。
- n⩾mn\geqslant{m}n⩾m仅是方程对每一点都有解的必要条件。这不是一个充分条件,因为有些列向量可能是冗余的。
- 假设有一个 R2×2\mathbb{R}^{2\times{2}}R2×2 中的矩阵,它的两个列向量是相同的。
- 那么它的列空间和它的一个列向量作为矩阵时的列空间是一样的。
- 换言之,虽然该矩阵有 2 列,但是它的列空间仍然只是一条线(只能描述某个方向),不能涵盖整个 R2\mathbb{R}^2R2 空间。
- n⩾mn\geqslant mn⩾m。否则,A 列空间的维数会小于 m。
范数
-
有时我们需要衡量一个向量的大小。
- 在机器学习中,我们经常使用被称为 范数(norm)的函数衡量向量大小。
-
严格地说,范数可以是满足以下性质的任意函数:
-
半范数:
- f(x)⩾0f(x)\geqslant{0}f(x)⩾0
- 半正定性
- f(x+y)⩽f(x)+f(y)f(x+y)\leqslant{f(x)+f(y)}f(x+y)⩽f(x)+f(y),(次可加性)
- 即三角不等式,
- 例如函数f(x)=∣x∣f(x)=|x|f(x)=∣x∣就满足∣x+y∣⩽∣x∣+∣y∣|x+y|\leqslant{|x|+|y|}∣x+y∣⩽∣x∣+∣y∣
- ∀a∈R,f(ax)=∣a∣f(x)\forall{a}\in\mathbb{R},f(ax)=|a|f(x)∀a∈R,f(ax)=∣a∣f(x)
- 具有绝对一次齐次性
- f(x)⩾0f(x)\geqslant{0}f(x)⩾0
-
范数是一个半范数加上额外性质:
- f(x)=0⇒x=0f(x)=0\Rightarrow{x=0}f(x)=0⇒x=0(正定性)
LpL^pLp范数
-
Lp範數 (wikipedia.org)
-
形式上,LpL^pLp 范数定义如下∣∣x∣∣p||x||_{p}∣∣x∣∣p:
-
∣∣x∣∣p=(∑i∣xi∣p)1p\large||x||_{p}=\left(\sum_{i}|x_i|^p\right)^{\frac{1}{p}} ∣∣x∣∣p=i∑∣xi∣pp1
- xix_ixi是向量xxx的元素
- 其中p∈R,p⩾1p\in\mathbb{R},p\geqslant{1}p∈R,p⩾1
- 1p∈(0,1]\frac{1}{p}\in(0,1]p1∈(0,1]
-
范数是将向量映射到非负值(容易证明Lp⩾0L^p\geqslant{0}Lp⩾0)
- 由幂函数的知识,在函数f(x)=xp(p>0)f(x)=x^p(p>0)f(x)=xp(p>0)是递增函数
- ∣xi∣⩾0|x_i|\geqslant{0}∣xi∣⩾0,则0=0p⩽∣xi∣p0=0^{p}\leqslant{|x_i|^p}0=0p⩽∣xi∣p
- 所以∑i∣xi∣p⩾0\sum_{i}|x_i|^p\geqslant{0}∑i∣xi∣p⩾0
- ∣∣x∣∣p⩾0||x||_p\geqslant{0}∣∣x∣∣p⩾0
-
补充:由指数函数知识,g(x)=tx(0<t<1)g(x)=t^x(0<t<1)g(x)=tx(0<t<1)是递减的,在t>1t>1t>1是递增的
- 如果∣xi∣<1|x_i|<1∣xi∣<1,则∑i∣xi∣p⩽∑i∣xi∣\sum_{i}|x_i|^p\leqslant{\sum_{i}|x_i|}∑i∣xi∣p⩽∑i∣xi∣
- 如果∣xi∣>1|x_i|>1∣xi∣>1,则:∑i∣xi∣p⩾∑i∣xi∣\sum_{i}|x_i|^p\geqslant{\sum_{i}|x_i|}∑i∣xi∣p⩾∑i∣xi∣
-
-
向量x的范数衡量从原点(零向量)到点x的距离
-
当p=2p=2p=2时,L2L^2L2范数被称为Euclidean norm(欧几里得范数)
-
∣∣x∣∣2||x||^2∣∣x∣∣2破坏了范数规则,比如次可加性
-
它表示从原点出发到向量xxx确定的点的欧几里得距离
-
欧几里得距离 (wikipedia.org)
-
对于n维向量空间,原点O=(0,0,⋯,0)O=(0,0,\cdots,0)O=(0,0,⋯,0)到x=(x1,x2,⋯,xn)x=(x_1,x_2,\cdots,x_n)x=(x1,x2,⋯,xn)描述的点的欧式距离
-
∥x⃗∥2=∣x1∣2+⋯+∣xn∣2\|{\vec {x}}\|_{2}={\sqrt {|x_{1}|^{2}+\cdots +|x_{n}|^{2}}} ∥x∥2=∣x1∣2+⋯+∣xn∣2
-
更一般的,从点ppp到qqq的欧几里得距离:
-
d(p,q)=∑i=1n(qi−pi)2d(\mathbf {p,q})= \sqrt{\sum \limits_{i=1}^n (q_i-p_i)^2} d(p,q)=i=1∑n(qi−pi)2
- p,qp,qp,q = two points in Euclidean n-space
qi,piq_i, p_iqi,pi = Euclidean vectors, starting from the origin of the space (initial point)
nnn = n-space
- p,qp,qp,q = two points in Euclidean n-space
-
或描述为:
d(x,y)=(x1−y1)2+(x2−y2)2+⋯+(xn−yn)2{\displaystyle d(x,y)={\sqrt {(x_{1}-y_{1})^{2}+(x_{2}-y_{2})^{2}+\cdots +(x_{n}-y_{n})^{2}}}} d(x,y)=(x1−y1)2+(x2−y2)2+⋯+(xn−yn)2
-
-
-
-
-
L2L^2L2 范数在机器学习中出现地十分频繁
- 平方L2L^2L2范数∣∣x∣∣22||x||_2^2∣∣x∣∣22,经常简化表示为 ∥x∥∥x∥∥x∥,略去了角标2
- 平方 L2L^2L2 范数也经常用来衡量向量的大小,可以简单地通过点积 (xTxx^TxxTx)计算。
- 平方 L2L^2L2 范数在数学和计算上都比 L2L^2L2 范数本身更方便。
- 例如,平方 L2L^2L2 范数对xxx中每个元素的导数只取决于对应的元素,
- 而 L2L^2L2 范数对每个元素的导数却和整个向量相关。
- 但是在很多情况下,平方 L2L^2L2 范数也可能不受欢迎,因为它在原点附近增长得十分缓慢。
- 例如,平方 L2L^2L2 范数对xxx中每个元素的导数只取决于对应的元素,
-
在某些机器学习应用中,区分恰好是零的元素和非零但值很小的元素是很重要的。
-
在这些情况下,我们转而使用在各个位置斜率相同,同时保持简单的数学形式的函数:L1 范数。
-
L1 范数可以简化如下:
- ∣∣x∣∣1=∑i∣xi∣||x||_1=\sum_i|x_i| ∣∣x∣∣1=i∑∣xi∣
-
-
最大范数
- ∣∣x∣∣∞=max(x1,x2,⋯,xn)或描述为:∥x⃗∥∞=limp→+∞(∑i=1n∣xi∣p)1/p=maxi∣xi∣||x||_{\infin}=max(x_1,x_2,\cdots,x_n) \\ 或描述为: \\ {\displaystyle \lVert {\vec {x}}\rVert _{\infty }=\lim _{p\to +\infty }{\Bigl (}\sum \limits _{i=1}^{n}|x_{i}|^{p}{\Bigr )}^{1/p}=\max _{i}|x_{i}|} ∣∣x∣∣∞=max(x1,x2,⋯,xn)或描述为:∥x∥∞=p→+∞lim(i=1∑n∣xi∣p)1/p=imax∣xi∣
向量点积用范数表示
-
xTy=∣∣x∣∣2∣∣y∣∣2cosθx^Ty=||x||_2||y||_2\cos{\theta} xTy=∣∣x∣∣2∣∣y∣∣2cosθ
- 其中θ\thetaθ表示x,yx,yx,y之间的夹角
ref
-
范数 (wikipedia.org)
-
范数(英语:Norm),是具有“长度”概念的函数。
- 在线性代数、泛函分析及相关的数学领域,是一个函数,其为向量空间内的所有向量赋予非零的正长度或大小。
-
另一方面,半范数(英语:seminorm)可以为非零的向量赋予零长度。
-
例,一个二维度的欧氏几何空间R2\mathbb {R} ^{2}R2就有欧氏范数。在这个向量空间的元素(譬如:(3,7))常常在笛卡尔坐标系统被画成一个从原点出发的箭号。每一个向量的欧氏范数就是箭号的长度。
拥有范数的向量空间就是赋范向量空间。同样,拥有半范数的向量空间就是赋半范向量空间。
衡量矩阵大小
-
有时候我们可能也希望衡量矩阵的大小。在深度学习中,最常见的做法是使用 Frobenius 范数(Frobenius norm)
-
∣∣A∣∣F=∑i,jAi,j2||A||_{F}=\sqrt{\sum\limits_{i,j}A^2_{i,j}} ∣∣A∣∣F=i,j∑Ai,j2
- 其中Ai,jA_{i,j}Ai,j是矩阵A的第i行第j列元素
-
其类似于L2L^2L2范数
-
特殊类型矩阵和向量
对角阵
-
Diagonal matrix - Wikipedia
-
Main diagonal - Wikipedia
-
对角矩阵(diagonal matrix)只在主对角线上含有非零元素,其他位置都是零。
-
形式上,设矩阵D满足,Dij=0D_{ij}=0Dij=0,if i≠ji\neq{j}i=j,则D是对角阵
-
啰嗦的讲:
- Dij={0,i≠jx,i=jx可以是任何数D_{ij}= \begin{cases} 0,&i\neq{j}\\ x,&i =j \end{cases} \quad x可以是任何数 Dij={0,x,i=ji=jx可以是任何数
-
-
矩阵主对角线上的元素是Dij,i=jD_{ij},i=jDij,i=j的元素
-
非方阵矩阵也有主对角线元素,并且主对角线长度取决于行数和列数种的较小者
-
[100010001][100001000010][100010001000][1000010000100001]{\displaystyle {\begin{bmatrix}\color {red}{1}&0&0\\0&\color {red}{1}&0\\0&0&\color {red}{1}\end{bmatrix}}\qquad {\begin{bmatrix}\color {red}{1}&0&0&0\\0&\color {red}{1}&0&0\\0&0&\color {red}{1}&0\end{bmatrix}}\qquad {\begin{bmatrix}\color {red}{1}&0&0\\0&\color {red}{1}&0\\0&0&\color {red}{1}\\0&0&0\end{bmatrix}}\qquad {\begin{bmatrix}\color {red}{1}&0&0&0\\0&\color {red}{1}&0&0\\0&0&\color {red}{1}&0\\0&0&0&\color {red}{1}\end{bmatrix}}\qquad } 1000100011000100010001000010000101000010000100001
- 主对角线元素用红色表出
- 且这些矩阵都是满足对角阵的定义(对于非方阵而言,对角阵的主对角线两侧0的分布不对称)
- 非零元素的占比:设q=min(m,n),其中m,n分别是对角阵D的行数和列数
- 则对角阵D种的非零元素比例不超过qq2=1q\frac{q}{q^2}=\frac{1}{q}q2q=q1
- 这是计算机计算对角阵乘法快速的原因之一
-
-
-
我们用 diag(v)diag(v)diag(v) 表示一个对角元素由向量 v 中元素给定的对角方阵。
-
对角矩阵受到关注的部分原因是对角矩阵的乘法计算很高效。
- 计算乘法 diag(v)xdiag(v)xdiag(v)x,我们只需要将 x 中的每个元素 xix_ixi 放大 viv_ivi 倍。换言之,diag(v)x=v⊙xdiag(v)x = v ⊙ xdiag(v)x=v⊙x。
- 计算对角方阵的逆矩阵也很高效。
- 在很多情况下,我们可以根据任意矩阵导出一些通用的机器学习算法;
- 但通过将一些矩阵限制为对角矩阵,我们可以得到计算代价较低的(并且简明扼要的)算法。
-
不是所有的对角矩阵都是方阵。🎈
- 长方形的矩阵也有可能是对角矩阵。
- 非方阵的对角矩阵没有逆矩阵,但我们仍然可以高效地计算它们的乘法。
- 对于一个长方形对角矩阵 D 而言,和向量xxx的乘法 DxDxDx 会涉及到向量xxx 中每个元素的缩放
- 如果 D 是瘦长型矩阵,那么在缩放后的末尾添加一些零;
- 如果 D 是胖宽型矩阵,那么在缩放后去掉最后一些元素。
向量长度
-
设向量α\alphaα是n维实向量,向量长度被定义为∣∣α∣∣=αTα||\alpha||=\sqrt{\alpha^T\alpha}∣∣α∣∣=αTα
-
若α=(a1,⋯,an)T\alpha=(a_1,\cdots,a_n)^Tα=(a1,⋯,an)T
-
则
∣∣a∣∣=∑iai2||a||=\sqrt{\sum_{i}a_i^2} ∣∣a∣∣=i∑ai2 -
对于记号∣∣α∣∣||\alpha||∣∣α∣∣有时被强调为∣∣α∣∣2||\alpha||_2∣∣α∣∣2(带上角标,L2L^{2}L2范数)
-
如果将α\alphaα是三维向量,那么将三维向量看作是空间中的一个点P坐标,则∣∣a∣∣||a||∣∣a∣∣描述的就是点P到原点的距离
-
性质
-
∣∣α∣∣⩾0||\alpha||\geqslant{0}∣∣α∣∣⩾0
- 仅当α=0\alpha=0α=0时∣∣α∣∣=0||\alpha||=0∣∣α∣∣=0
-
∣∣kα∣∣=∣k∣⋅∣∣α∣∣,k∈R||k\alpha||=|k|\cdot{||\alpha||},k\in{\mathbb{R}}∣∣kα∣∣=∣k∣⋅∣∣α∣∣,k∈R
- ∣∣ka∣∣=∑i(kai)2=∑k2ai2=k2∑ai2=∣k∣∑iai2=∣k∣⋅∣∣α∣∣||ka||=\sqrt{\sum_{i}(ka_i)^2}=\sqrt{\sum k^2{a_{i}^2}} \\=\sqrt{k^2\sum {a_{i}^2}} =|k|\sqrt{\sum_{i}a_i^2} =|k|\cdot{||\alpha||} ∣∣ka∣∣=i∑(kai)2=∑k2ai2=k2∑ai2=∣k∣i∑ai2=∣k∣⋅∣∣α∣∣
单位向量
-
单位向量(unit vector)是具有单位范数(unit norm)的向量:
- ∥x∥2=1∥x∥_2 = 1 ∥x∥2=1
向量单位化(正规化)
-
非单位向量可以通过正规化得到同方向的单位向量
-
对于任意非零向量α\alphaα,
- β=1∣∣α∣∣α的长度一定是1∣∣β∣∣=∣∣1∣∣α∣∣α∣∣=1∣∣α∣∣∣∣α∣∣=1\beta=\frac{1}{||\alpha||}\alpha的长度一定是1 \\ ||\beta||=\left|\left|\frac{1}{||\alpha||}\alpha\right|\right| =\frac{1}{||\alpha||}||\alpha||=1 β=∣∣α∣∣1α的长度一定是1∣∣β∣∣=∣∣α∣∣1α=∣∣α∣∣1∣∣α∣∣=1
正交
向量正交
-
如果 (x,y)=xTy=0(x,y)=x^Ty = 0(x,y)=xTy=0,那么向量 x 和向量 y 互相 正交(orthogonal),记为x⊥yx\perp{y}x⊥y
- 如果两个向量都有非零范数(长度大于0),那么这两个向量之间的夹角是 90 度。
-
在 Rn\mathbb{R}^nRn 中,至多有 n 个范数非零向量互相正交。
- 如果这些向量不仅互相正交,并且范数都为 1,那么我们称它们是 标准正交(orthonormal)。
正交向量组
-
若Φ=α1⋯,αn\Phi=\alpha_1\cdots,\alpha_nΦ=α1⋯,αn,αi≠0,i=1,2,⋯,n\alpha_i\neq{0},i=1,2,\cdots,nαi=0,i=1,2,⋯,n中向量两两正交,(αi,αj)=0,(i≠j),i,j=1,2,⋯,n(\alpha_i,\alpha_j)=0,(i\neq{j}),i,j=1,2,\cdots,n(αi,αj)=0,(i=j),i,j=1,2,⋯,n,则称Φ\PhiΦ是一个正交向量组
-
显然有
- (αi,αj){0,i≠jR+,i=jR+>0(\alpha_i,\alpha_j) \begin{cases} 0,&i\neq{j}\\ R^+,&i=j \end{cases} \\R^+>0 (αi,αj){0,R+,i=ji=jR+>0
-
-
正交向量组Φ⊥\Phi_{\perp}Φ⊥线性无关
-
证明
-
设β=αp,p∈{1,2,⋯,n}\beta=\alpha_{p},p\in\{1,2,\cdots,n\}β=αp,p∈{1,2,⋯,n}
-
设存在常数K=k1,⋯,knK=k_1,\cdots,k_nK=k1,⋯,kn
-
∑inkiαi=0\sum_{i}^{n}k_i\alpha_i=0∑inkiαi=0
-
两边同时和β\betaβ做内积
-
(β,∑inkiαi)=0(\beta,\sum_{i}^{n}k_i\alpha_i)=0(β,∑inkiαi)=0
-
∑in(β,kiαi)=∑inki(β,αi)=0\sum_i^n(\beta,k_i\alpha_i) =\sum_i^nk_i(\beta,\alpha_i)=0 i∑n(β,kiαi)=i∑nki(β,αi)=0
-
-
由于
- (αp,αi)=0(\alpha_p,\alpha_i)=0(αp,αi)=0,if p≠ip\neq{i}p=i
- (αp,αi)>0(\alpha_p,\alpha_i)>0(αp,αi)>0,if p=ip=ip=i
-
所以
-
ki(β,αi)=0,i≠pk_i(\beta,\alpha_i)=0,i\neq{p} ki(β,αi)=0,i=p
- 或者描述为:
或kp‾(αp,αp‾)=0或k−p(αp,α−p)=0p‾和−p都表示不等于p的数或\Large k_{\overline{p}}(\alpha_p,\alpha_{\overline{p}})=0 \\ 或\Large k_{-p}(\alpha_p,\alpha_{-{p}})=0 \\ \overline{p}和-p都表示不等于p的数 或kp(αp,αp)=0或k−p(αp,α−p)=0p和−p都表示不等于p的数
- 或者描述为:
-
kp(β,αp)=0,kp=0k_p(\beta,\alpha_p)=0,k_p=0kp(β,αp)=0,kp=0🎈
-
-
类似的,当β=αp\beta=\alpha_pβ=αp,p取遍1,2,⋯,n1,2,\cdots,n1,2,⋯,n,可得k1=k2=⋯=kn=0k_1=k_2=\cdots=k_n=0k1=k2=⋯=kn=0
-
-
标准正交基
-
设正交向量组Φ\PhiΦ的每个向量都是单位向量,则称Φ\PhiΦ为标准正交基(规范正交基),还可以描述为:
-
(αi,αj)=δij={1,i=j0,i≠j(i,j=1,2,⋯<n)(\alpha_i,\alpha_j)=\delta_{ij} =\begin{cases} 1,&i=j\\ 0,&i\neq{j} \end{cases} \quad(i,j=1,2,\cdots<n) (αi,αj)=δij={1,0,i=ji=j(i,j=1,2,⋯<n)
-
专用符号δij\delta_{ij}δij是Kronecker符号
-
正交化(schmidt)
-
一个向量组线性无关是该型两组称为正交向量组的必要条件(却不充分条件)
-
对于一个线性无关组Φ\PhiΦ,可以通过施密特正交化方法,求出一个等价的正交向量组Ψ\PsiΨ,Ψ∼Φ\Psi\sim{\Phi}Ψ∼Φ
- 这是一种递推计算的方法
-
设Φ=(α1,α2,⋯,αn)\Phi=(\alpha_1,\alpha_2,\cdots,\alpha_n)Φ=(α1,α2,⋯,αn)
-
令
- βi=αi−∑i=1s((αi,βi−1)βi−1,βi−1)βi−1=αi−∑i=1n(αi,βi−1)∣∣βi−1∣∣2βi−1令β0=0i=1,2,⋯,n\beta_{i}=\alpha_i-\sum_{i=1}^{s}(\frac{(\alpha_i,\beta_{i-1})}{\beta_{i-1},\beta_{i-1}})\beta_{i-1} \\=\alpha_i-\sum_{i=1}^{n}\frac{(\alpha_i,\beta_{i-1})}{||\beta_{i-1}||^2}\beta_{i-1} \\令\beta_0=0 \\ i=1,2,\cdots,n βi=αi−i=1∑s(βi−1,βi−1(αi,βi−1))βi−1=αi−i=1∑n∣∣βi−1∣∣2(αi,βi−1)βi−1令β0=0i=1,2,⋯,n
-
令Ψ=β1,⋯,βn\Psi=\beta_1,\cdots,\beta_nΨ=β1,⋯,βn,Ψ\PsiΨ正交向量组
-
则Ψ≅Φ\Psi\cong{\Phi}Ψ≅Φ(等价)
-
正交矩阵
-
正交矩阵是一种特殊的可逆矩阵
-
设n阶方阵A满足ATA=EA^TA=EATA=E(或AAT=EAA^T=EAAT=E),则称A是正交矩阵(正交阵)
-
正交矩阵的逆:A−1=ATA^{-1}=A^TA−1=AT
- 由(ATA)=E(A^TA)=E(ATA)=E和可逆矩阵的定义可以推出AT=A−1A^T=A^{-1}AT=A−1
- 即有A−1A=AA−1=EA^{-1}A=AA^{-1}=EA−1A=AA−1=E
- 因此ATA=AAT=EA^TA=AA^T=EATA=AAT=E
- 由(ATA)=E(A^TA)=E(ATA)=E和可逆矩阵的定义可以推出AT=A−1A^T=A^{-1}AT=A−1
-
A−1A^{-1}A−1依然是正交矩阵
- A−1=ATA^{-1}=A^TA−1=AT
- 因为(A−1)T=(AT)T=A(A^{-1})^T=(A^T)^T=A(A−1)T=(AT)T=A
- (A−1)T(A−1)=AAT=E(A^{-1})^T(A^{-1})=AA^T=E(A−1)T(A−1)=AAT=E
- 所以A−1A^{-1}A−1依然可逆
-
∣A∣=1|A|=1∣A∣=1
- ∣ATA∣=∣E∣|A^TA|=|E|∣ATA∣=∣E∣
- ∣AT∣∣A∣=1|A^T||A|=1∣AT∣∣A∣=1
- ∣AT∣=∣A∣,∣A∣2=1|A^T|=|A|,|A|^2=1∣AT∣=∣A∣,∣A∣2=1
- ∣A∣=±1|A|=\pm 1∣A∣=±1
-
(A∗)TA∗=E(A^*)^TA^*=E(A∗)TA∗=E
- 证明:
- A−1=∣A∣−1A∗A^{-1}=|A|^{-1}A^{*}A−1=∣A∣−1A∗
- (A−1)T(A−1)=E(A^{-1})^T(A^{-1})=E(A−1)T(A−1)=E
- (∣A∣−1A∗)T∣A∣−1A∗=E(|A|^{-1}A^{*})^T|A|^{-1}A^{*}=E(∣A∣−1A∗)T∣A∣−1A∗=E
- ∣A∣−1(A∗)T∣A∣−1A∗=E|A|^{-1}(A^*)^T|A|^{-1}A^*=E∣A∣−1(A∗)T∣A∣−1A∗=E
- ∣A∣2=1|A|^2=1∣A∣2=1
- ∣A∣−2=1|A|^{-2}=1∣A∣−2=1
- (A∗)TA∗=E(A^*)^TA^*=E(A∗)TA∗=E
- 证明:
-
设A,B为同阶正交矩阵,ATA=E,BTB=EA^TA=E,B^TB=EATA=E,BTB=E,则对于C=ABC=ABC=AB,有CTC=EC^TC=ECTC=E
- (AB)T(AB)=BTATAB=BT(ATA)B=BTEB=BTB=E(AB)^T(AB)=B^TA^TAB=B^T(A^TA)B=B^TEB=B^TB=E(AB)T(AB)=BTATAB=BT(ATA)B=BTEB=BTB=E
- 因此(AB)(AB)(AB)为正交矩阵
矩阵是正交矩阵的充要条件
-
n阶方阵Q的行(列)向量组是标准正交基是Q为正交矩阵的充要条件
-
设Q=(α1,⋯,αn)TQ=(\alpha_1,\cdots,\alpha_n)^TQ=(α1,⋯,αn)T
- αi\alpha_iαi是行向量
-
QT=(α1T,⋯,αnT)Q^T=(\alpha_1^T,\cdots,\alpha_n^T)QT=(α1T,⋯,αnT)
- αiT\alpha_i^TαiT是列向量
-
QQT=QTQ=EQQ^T=Q^TQ=EQQT=QTQ=E
-
QQT=(α1α2⋮αn)(α1T,⋯,αnT)=(α1α1Tα1α2T⋯α1αnTα2α1Tα2α2T⋯α2αnT⋮⋮⋮αnα1Tαnα2T⋯αnαnT)=E=(10⋯001⋯0⋮⋮⋮00⋯1)QQ^T= \begin{pmatrix} \alpha_1\\ \alpha_2\\ \vdots\\ \alpha_n \end{pmatrix} (\alpha_1^T,\cdots,\alpha_n^T) \\ =\begin{pmatrix} \alpha_1\alpha_1^T&\alpha_1\alpha_2^T&\cdots&\alpha_1\alpha_n^T\\ \alpha_2\alpha_1^T&\alpha_2\alpha_2^T&\cdots&\alpha_2\alpha_n^T\\ \vdots&\vdots&&\vdots\\ \alpha_n\alpha_1^T&\alpha_n\alpha_2^T&\cdots&\alpha_n\alpha_n^T \end{pmatrix} =E= \begin{pmatrix} 1&0&\cdots&0\\ 0&1&\cdots&0\\ \vdots&\vdots&&\vdots\\ 0&0&\cdots&1 \end{pmatrix} QQT=α1α2⋮αn(α1T,⋯,αnT)=α1α1Tα2α1T⋮αnα1Tα1α2Tα2α2T⋮αnα2T⋯⋯⋯α1αnTα2αnT⋮αnαnT=E=10⋮001⋮0⋯⋯⋯00⋮1
-
αiαjT=(αi,αj)={1,i=j0,i≠j(i,j=1,2,⋯,n)\alpha_i\alpha_j^T=(\alpha_i,\alpha_j) =\begin{cases} 1,&i=j\\ 0,&i\neq{j} \end{cases} \quad(i,j=1,2,\cdots,n) \\ αiαjT=(αi,αj)={1,0,i=ji=j(i,j=1,2,⋯,n)
-
说明矩阵QQQ的行向量组α1,⋯,αn\alpha_1,\cdots,\alpha_nα1,⋯,αn是标准正交向量组
-
-
类似的
- 对于QTQ=EQ^TQ=EQTQ=E,QTQ^TQT的行向量组β1,⋯,βn\beta_1,\cdots,\beta_nβ1,⋯,βn是标准正交向量组
- 而QTQ^TQT的行向量就是Q的列向量,因此Q的列向量也是标准正交向量组
-
如果Q的行向量组是标准正交向量组,那么Q是正交矩阵
-
设Q的行向量组为Φ=α1,⋯,αn\Phi=\alpha_1,\cdots,\alpha_nΦ=α1,⋯,αn,Φ\PhiΦ是个标准正交向量组,则
- (αi,αj)={1,i=j0,i≠j(i,j=1,2,⋯,n)(αi,αj)=αiαjT即:(α1α1Tα1α2T⋯α1αnTα2α1Tα2α2T⋯α2αnT⋮⋮⋮αnα1Tαnα2T⋯αnαnT)=(10⋯001⋯0⋮⋮⋮00⋯1)(α1α2⋮αn)(α1T,⋯,αnT)=EQQT=E所以Q是正交矩阵(\alpha_i,\alpha_j) =\begin{cases} 1,&i=j\\ 0,&i\neq{j} \end{cases} \quad(i,j=1,2,\cdots,n) \\ (\alpha_i,\alpha_j)=\alpha_i\alpha_{j}^T \\ 即:\begin{pmatrix} \alpha_1\alpha_1^T&\alpha_1\alpha_2^T&\cdots&\alpha_1\alpha_n^T\\ \alpha_2\alpha_1^T&\alpha_2\alpha_2^T&\cdots&\alpha_2\alpha_n^T\\ \vdots&\vdots&&\vdots\\ \alpha_n\alpha_1^T&\alpha_n\alpha_2^T&\cdots&\alpha_n\alpha_n^T \end{pmatrix} =\begin{pmatrix} 1&0&\cdots&0\\ 0&1&\cdots&0\\ \vdots&\vdots&&\vdots\\ 0&0&\cdots&1 \end{pmatrix} \\ \begin{pmatrix} \alpha_1\\ \alpha_2\\ \vdots\\ \alpha_n \end{pmatrix} (\alpha_1^T,\cdots,\alpha_n^T)=E \\QQ^T=E \\所以Q是正交矩阵 (αi,αj)={1,0,i=ji=j(i,j=1,2,⋯,n)(αi,αj)=αiαjT即:α1α1Tα2α1T⋮αnα1Tα1α2Tα2α2T⋮αnα2T⋯⋯⋯α1αnTα2αnT⋮αnαnT=10⋮001⋮0⋯⋯⋯00⋮1α1α2⋮αn(α1T,⋯,αnT)=EQQT=E所以Q是正交矩阵
-
类似的QTQ^TQT的行向量组是标准正交向量组,则QTQ=EQ^TQ=EQTQ=E
- QTQ^TQT的行向量组就是Q的列向量组,从而Q的列向量组是表征正交向量组可以推出Q是正交矩阵
-
-
对称矩阵
- 若方阵A满足AT=AA^T=AAT=A,则AAA是对称阵
- aij=aji,(i,j=1,2,⋯n)a_{ij}=a_{ji},(i,j=1,2,\cdots{n})aij=aji,(i,j=1,2,⋯n)
- 若方阵A满足AT=−AA^T=-AAT=−A,则AAA是反对称阵
- aij=−aji,(i,j=1,2,⋯n)a_{ij}=-a_{ji},(i,j=1,2,\cdots{n})aij=−aji,(i,j=1,2,⋯n)
- 反对称阵的主对角线全为0
正交相似
- 如果方阵A:Q−1AQ=BQ^{-1}AQ=BQ−1AQ=B,(Q为正交矩阵(QTQ=EQ^TQ=EQTQ=E),则称A(关于Q)正交相似于BBB
概念区分🎈
-
区分相似对角化和正交相似
- 基本相似A∼BA\sim{B}A∼B:P−1AP=BP^{-1}AP=BP−1AP=B
- 相似对角化要求B是某个对角阵Λ\LambdaΛ
- 后者要求P是个正交矩阵(PTP=EP^TP=EPTP=E)
- 基本相似A∼BA\sim{B}A∼B:P−1AP=BP^{-1}AP=BP−1AP=B
-
另外还要区分对称和正交,两者都涉及到方阵的转置
-
不是所有方阵都可以对角化
正交相似对角化
- 对于方阵A,存在正交矩阵Q,使得Q−1AQ=ΛQ^{-1}AQ=\LambdaQ−1AQ=Λ,则A可以被正交相似对角化(简称正交对角化)
实对称方阵A正交对角化方法
- 求出实对称阵A的全部特征值(对称阵才可以正交对角化)
- 如果特征值λi\lambda_iλi是单根,则从f(λi)=0,即(λiE−A)x=0f(\lambda_i)=0,即(\lambda_iE-A)x=0f(λi)=0,即(λiE−A)x=0对应的求出一个特征向量αi\alpha_iαi
- 如果特征值λi\lambda_iλi是nin_ini重根,
- 则从f(λi)=0f(\lambda_i)=0f(λi)=0求出nin_ini个线性无关特征向量Φi=αi1,⋯,αni\Phi_i=\alpha_{i_1},\cdots,\alpha_{n_i}Φi=αi1,⋯,αni
- 对Φi\Phi_iΦi执行Schmidt正交化
- 在执行Normalization单位化
- 将得到的所有向量依此排列起来得到正交矩阵Q=(α1,⋯,αn)(\alpha_1,\cdots,\alpha_n)(α1,⋯,αn)
相关文章:

LA@生成子空间@范数@衡量矩阵大小@正交化
文章目录线性组合与线性方程组生成子空间范数LpL^pLp范数向量点积用范数表示ref衡量矩阵大小特殊类型矩阵和向量对角阵向量长度性质单位向量向量单位化(正规化)正交向量正交正交向量组标准正交基正交化(schmidt)正交矩阵矩阵是正交矩阵的充要条件对称矩阵正交相似概念区分&…...

MT2012_竹鼠的白色季节
竹鼠的白色季节 #include<bits/stdc.h> #include<algorithm> using namespace std;/*思路:从小到大排序,然后依次往后遍历即可*/ int main( ) {int n,d;cin>>n>>d; int tmp;vector<int>nums;for(int i0;i<n;i){cin&…...

MySQL是什么?它有什么优势?
随着时间的推移,开源数据库在中低端应用中逐渐流行起来,占据了很大的市场份额。开源数据库具有免费使用、配置简单、稳定性好、性能优良等特点,而 MySQL 数据库正是开源数据库中的杰出代表。 开源全称为“开放源代码”。很多人认为开源软件最…...
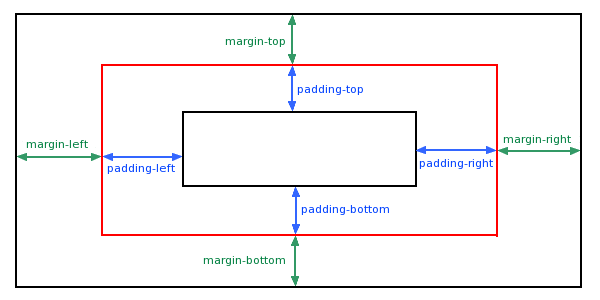
基础篇—CSS padding(填充\内边距)解析
CSS padding(填充) CSS padding(填充)是一个简写属性,定义元素边框与元素内容之间的空间,即上下左右的内边距。 属性说明padding使用简写属性设置在一个声明中的所有填充属性padding-bottom设置元素的底部填充padding-left设置元素的左部填充padding-right设置元素的右部…...

二进制枚举
一、左移:用来将一个数的各二进制位全部左移n位,低位以0补充,高位越界后舍弃。n左移1位,n<<1,相当于2*n1左移n位,1<<n,相当于2^n二、右移:将一个数的各二进制位右移N位&…...
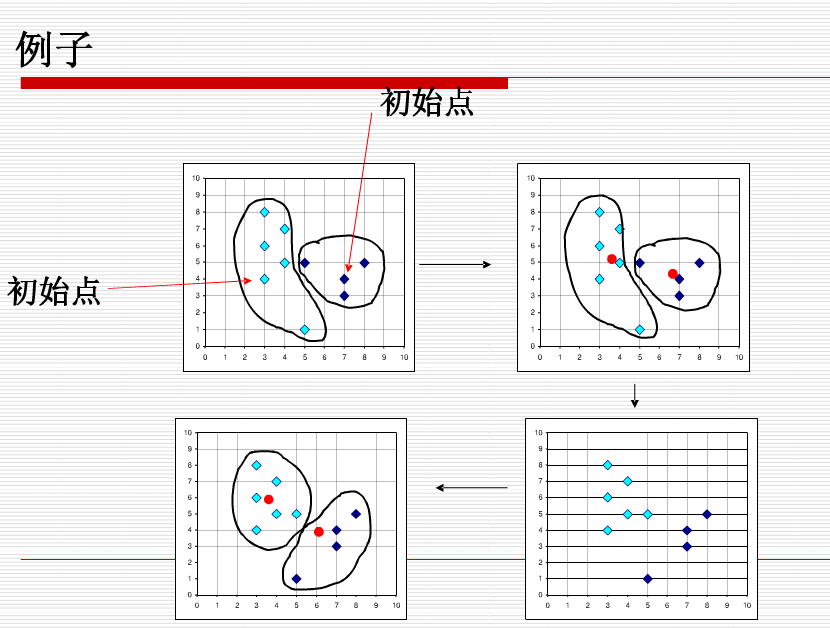
2|数据挖掘|聚类分析|k-means/k-均值算法
k-means算法k-means算法,也被称为k-平均或k-均值,是一种得到最广泛应用的聚类算法。算法首先随机选择k个对象,每个对象初始地代表了一个簇的平均值或中心。对剩余的每个对象根据其与各个簇中心的距离,将它赋给最近的簇。然后重新计…...
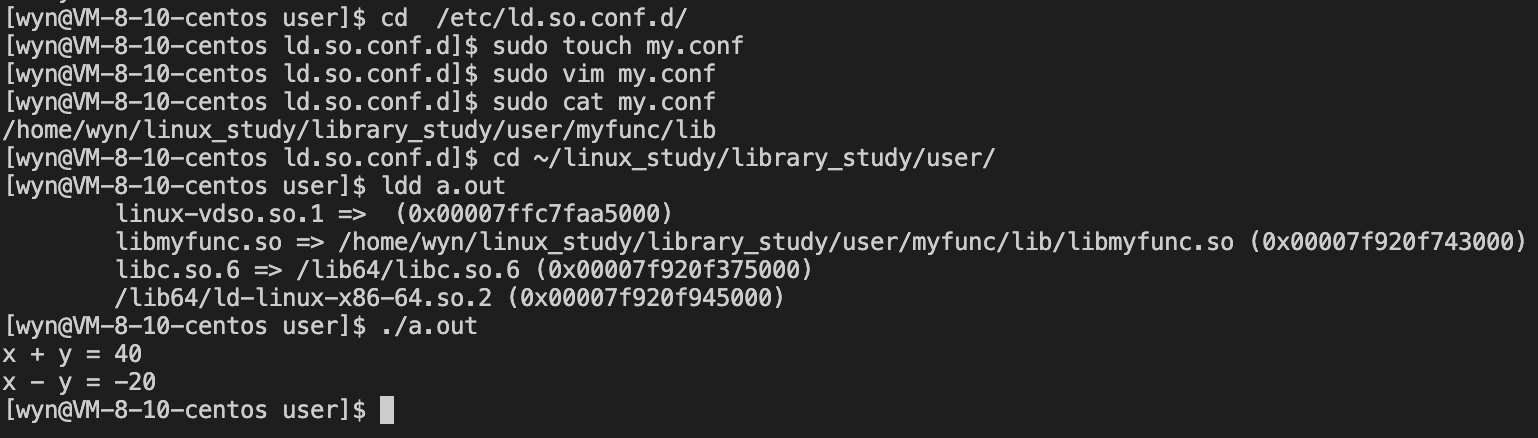
使用和制作动、静态库
文章目录什么是库?静态库打包方式使用方式生成并执行可执行程序粗暴方式优化方式动态库不一样的.o文件打包方式使用方式生成可执行程序运行可执行程序无法运行时的解决方案动静态库与动静态链接什么是库? 从一开始的helloworld,到现在熟练使…...

【Java基础】023 -- 集合进阶(List、Set、泛型、树)
目录 一、集合的体系结构 1、单列集合(Collection) 二、Collection集合 1、Collection常见方法 ①、代码实现: ②、contains方法重写equals方法示例:(idea可自动重写) 2、Collection的遍历方式(…...
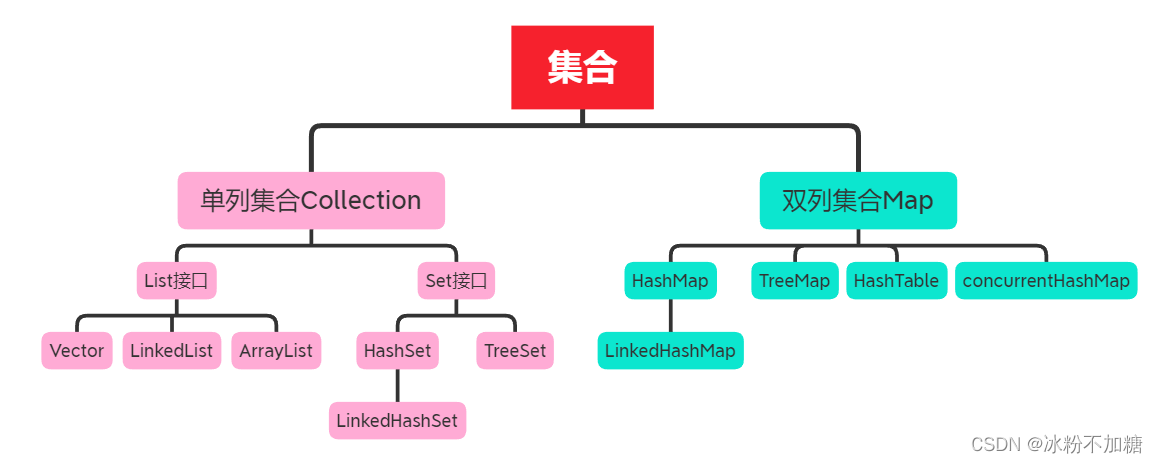
面试题整理01-集合详解
文章目录前言一、集合的整体结构单列集合接口:双列集合接口:二、单列集合详解1.List接口1.1 ArrayList集合特点:扩容:添加元素遍历1.2 LinkedList集合特点:添加元素:2.Set接口2.1 HashSet集合特点ÿ…...
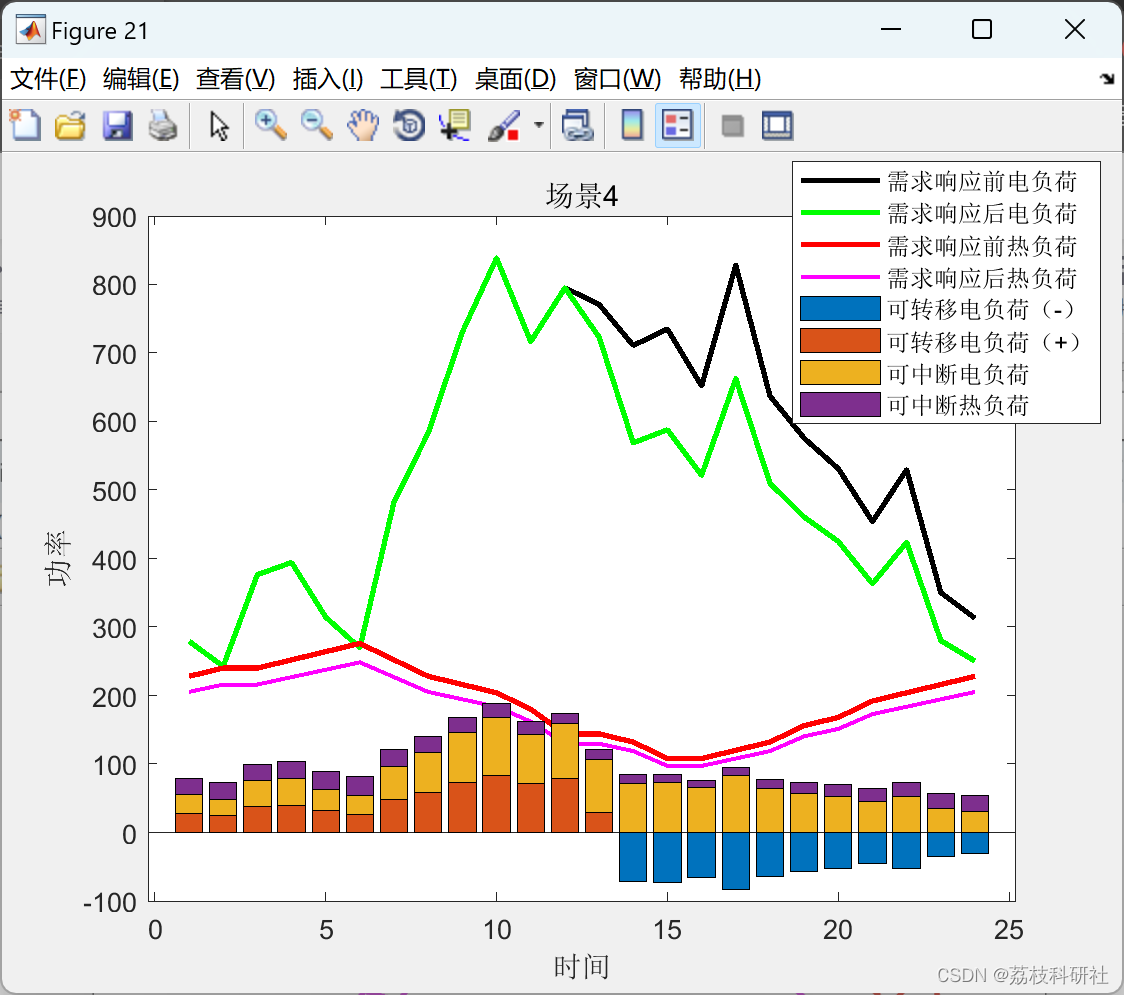
数据驱动的两阶段分布鲁棒(1-范数和∞-范数约束)的电热综合能源系统研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

ArcGIS网络分析之发布网络分析服务(二)
在上一篇中讲述了如何构建网络分析数据集,本篇将讲解如何发布网络分析服务。本文将使用上一篇中建立的网络数据集,下载地址在上一篇博文的最后已给出。 之前我们已经实现了基于ArcMap中的网络分析,但是仅仅支持本地是万万不够的,这里我们的目的就是将我们建好的网络分析图…...

js实现元素样式切换的基本功能
需求:用户第一次点击某些元素,改变元素的某些样式,比如背景颜色,字体颜色。用户第二次点击某些元素,恢复之前的样式。.....思路:准备一定量的div盒子,并取相同的类名<div class"box&quo…...

java 策略模式 + 工厂模式 实例
一 前言 经常听说各种设计模式,知道理论,也知道应该使用,但具体怎么用,什么时候用,使用的优点一直比较模糊,今天写一个项目中经常用到的模式,来具体理解。项目中经常用到工厂模式或者策略模式&…...
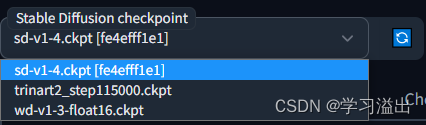
本地生成动漫风格 AI 绘画 图像|Stable Diffusion WebUI 的安装和部署教程
Stable Diffusion WebUI 的安装和部署教程1. 简介2. Windows安装环境3. 运行4. 模型下载链接5. 其他资源1. 简介 先放一张WebUI的图片生成效果图,以给大家学习的动力 :) 怎么样,有没有小小的心动?这里再补充一下&…...

华为OD机试 - 异常的打卡记录 | 备考思路,刷题要点,答疑 【新解法】
最近更新的博客 【新解法】华为OD机试 - 关联子串 | 备考思路,刷题要点,答疑,od Base 提供【新解法】华为OD机试 - 停车场最大距离 | 备考思路,刷题要点,答疑,od Base 提供【新解法】华为OD机试 - 任务调度 | 备考思路,刷题要点,答疑,od Base 提供【新解法】华为OD机试…...
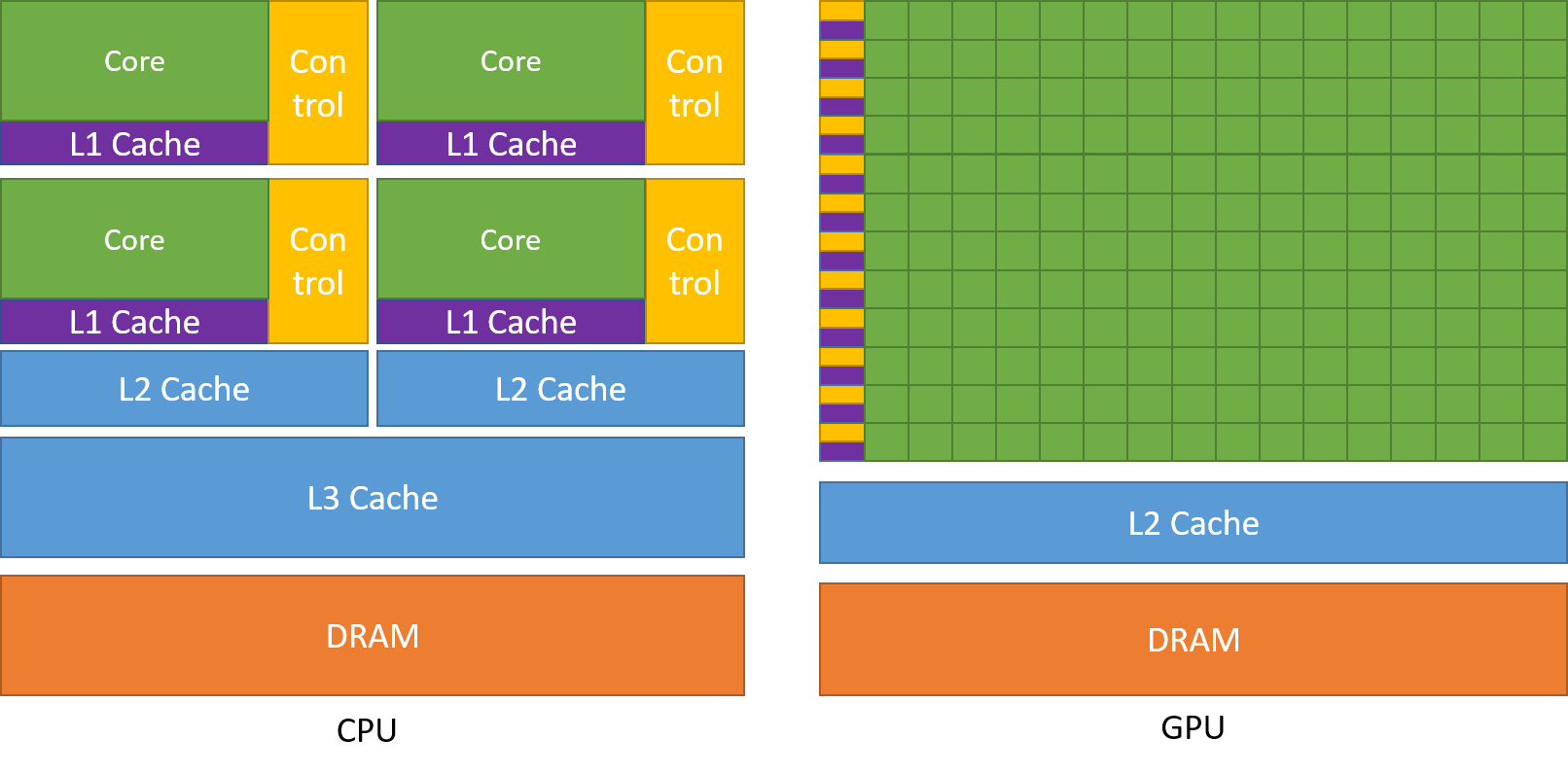
「机器学习笔记」之深度学习基础概念(基于Pytorch)
本文以 Pytorch 为线索,介绍人工智能和深度学习相关的一些术语、概念。 关于发展历史您也可以阅读深度学习神经网络之父 Jrgen Schmidhuber 所写的《Annotated History of Modern AI and Deep Learning(现代人工智能和深度学习的注释版历史)…...
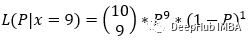
概率和似然
在日常生活中,我们经常使用这些术语。但是在统计学和机器学习上下文中使用时,有一个本质的区别。本文将用理论和例子来解释概率和似然之间的关键区别。 概率与似然 假设在一场棒球比赛中,两队的队长都被召集到场上掷硬币。获胜的队长将根据掷…...
前期软件项目评估偏差,如何有效处理?
1、重新评估制定延期计划 需要对项目进行重新评估,将新的评估方案提交项目干系人会议,开会协商一致后按照新的讨论结果制定计划,并实施执行。 软件项目评估偏差 怎么办:重新评估制定延期计划2、申请加资源 如果项目客户要求严格&a…...

Xline v0.2.0: 一个用于元数据管理的分布式KV存储
Xline是什么?我们为什么要做Xline? Xline是一个基于Curp协议的,用于管理元数据的分布式KV存储。现有的分布式KV存储大多采用Raft共识协议,需要两次RTT才能完成一次请求。当部署在单个数据中心时,节点之间的延迟较低&a…...

CompletableFuture
一、一个示例回顾Future 一些业务场景我们需要使用多线程异步执行任务,加快任务执行速度。JDK5新增了Future接口,用于描述一个异步计算的结果。虽然Future以及相关使用方法提供了异步执行任务的能力,但是对于结果的获取却是很不方便,我们必须使用Future.get()的方式阻塞调…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...
