清风1.层次分析法
一.流程
1.建立评价体系
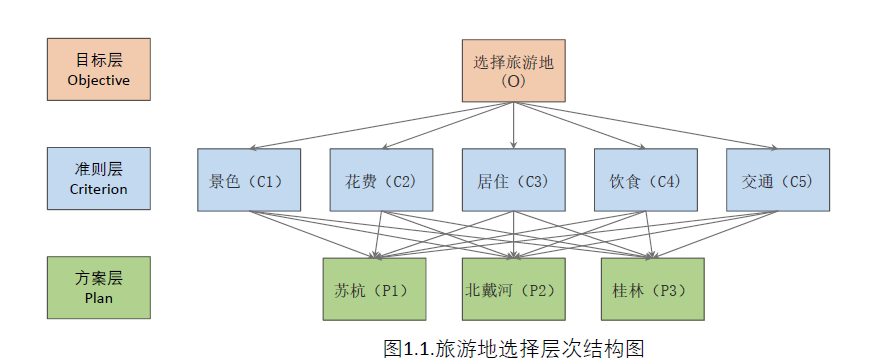
2.建立判断矩阵
2.1 A-C-C矩阵
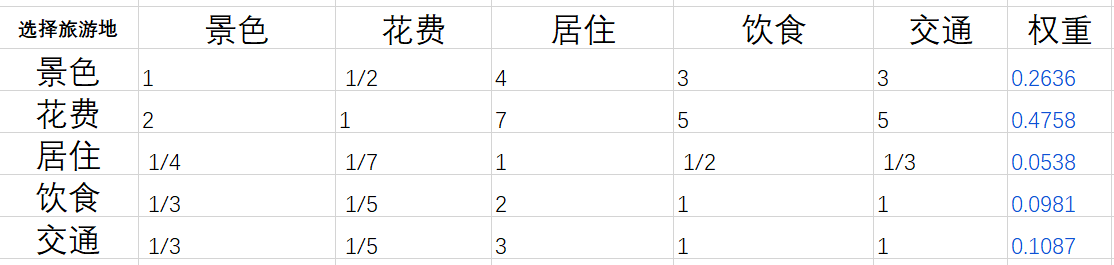
从准则层对目标层的特征向量上看,花费的权重最大
算术平均法求权重的结果为:
0.2623
0.4744
0.0545
0.0985
0.1103
几何平均法求权重的结果为:
0.2636
0.4773
0.0531
0.0988
0.1072
特征值法求权重的结果为:
0.2636
0.4758
0.0538
0.0981
0.1087
一致性指标CI=
0.0180
一致性比例CR=
0.0161
因为CR<0.10,所以该判断矩阵A的一致性可以接受!
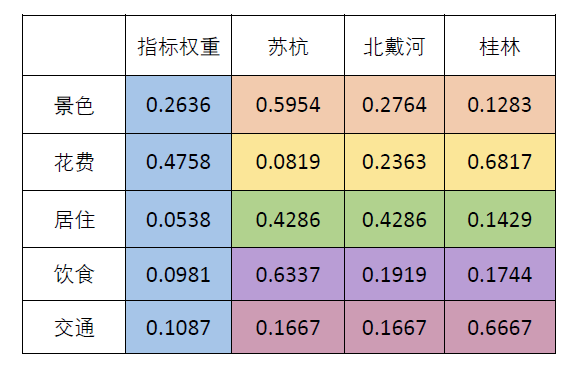
2.2 Ci-P-P矩阵

从方案层对目标层的权重上看,桂林的权重最大(以C层最大的花费为Ci,两层权重的乘积)
算术平均法求权重的结果为:
0.5949
0.2766
0.1285
几何平均法求权重的结果为:
0.5954
0.2764
0.1283
特征值法求权重的结果为:
0.5954
0.2764
0.1283
一致性指标CI=
0.0028
一致性比例CR=
0.0053
因为CR<0.10,所以该判断矩阵A的一致性可以接受!
3.计算评分及排序
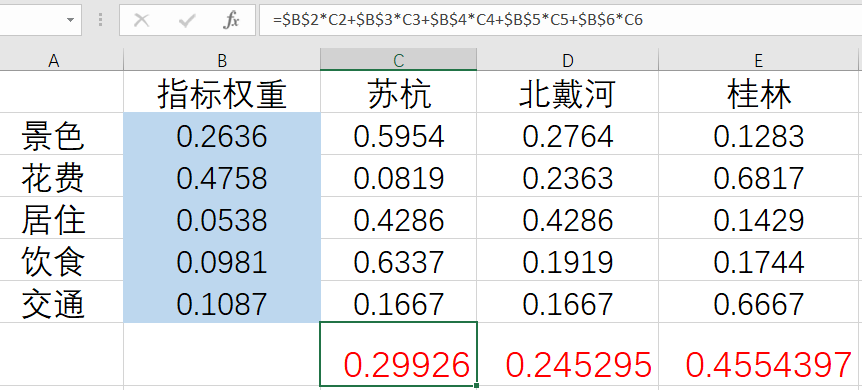
计算:
fn+F4锁定单元格
排序:
选择性粘贴:数值
粘贴中转置,再排序
二.论文
考虑到层次分析法构造时的主观色彩比较强,我们又利用熵值取权法给出了客观条件下的一组权值w2,对w1进行修正
通过判断各个因素的变化剧烈程度来决定该因素在最终目标中所占的权重
比如国家的财政支持对高等院校的学费的制定影响很重要,但是如果财政支持费用10年都不变,而家庭支付承受能力虽然对学费的制定没有国家财政支持的影响那么重要,但是它每年都在快速的增加,从熵值取权法的角度来看这时家庭的支付承受能力的影响就比国家财政的支持大,这与客观的人们的想法也是一样,同时它和层次分析法得出的结论是互补的且是客观的。
我们利用熵值取权法客观地给出一个5个因素的1×5的权重矩阵w2,对由层次分析法给出的1×5的权重矩阵w1,以0.2:0.8的比例进行修正,从而给出最终的5个因素对合理化指数的组合权重值阵 W=0.8×w1+0.2×w2
相关文章:

清风1.层次分析法
一.流程1.建立评价体系2.建立判断矩阵2.1 A-C-C矩阵从准则层对目标层的特征向量上看,花费的权重最大算术平均法求权重的结果为:0.26230.47440.05450.09850.1103几何平均法求权重的结果为:0.26360.47730.05310.09880.1072特征值法求权重的结果…...

「首席架构师推荐」免费数据可视化软件你喜欢哪一个?
数据可视化,是关于数据视觉表现形式的科学技术研究。其中,这种数据的视觉表现形式被定义为,一种以某种概要形式抽提出来的信息,包括相应信息单位的各种属性和变量。它是一个处于不断演变之中的概念,其边界在不断地扩大…...

深度学习术语解释:backbone、head、neck,etc
backbone:翻译为主干网络的意思,既然说是主干网络,就代表其是网络的一部分,那么是哪部分呢?这个主干网络大多时候指的是提取特征的网络,其作用就是提取图片中的信息,共后面的网络使用。这些网络…...
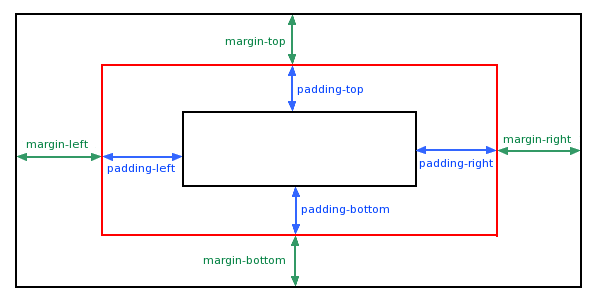
基础篇—CSS margin(外边距)解析
什么是CSS margin(外边距)? CSS margin(外边距)属性定义元素周围的空间。 属性描述margin简写属性。在一个声明中设置所有外边距属性。margin-bottom设置元素的下外边距。margin-left设置元素的左外边距。margin-right设置元素的右外边距。margin-top设置元素的上外边距。mar…...

ChatGPT或将引发新一轮失业潮?是真的吗?
最近,要说有什么热度不减的话题,那ChatGPT必然榜上有名。据悉是这是由美国人工智能研究实验室OpenAI开发的一种全新聊天机器人模型,它能够通过学习和理解人类的语言来进行对话,还能根据聊天的上下文进行互动,并协助人类…...
【Selenium学习】Selenium 中特殊元素操作
1.鼠标定位操作鼠标悬停,即当光标与其名称表示的元素重叠时触发的事件,在 Selenium 中将键盘鼠标操作封装在 Action Chains 类中。Action Chains 类的主要应用场景为单击鼠标、双击鼠标、鼠标拖曳等。部分常用的方法使用分类如下:• click(on…...

Spark相关的依赖冲突,后期持续更新总结
Spark相关的依赖冲突持续更新总结 Spark-Hive_2.11依赖报错 这个依赖是Spark开启支持hive SQL解析,其中2.11是Spark对应的Scala版本,如Spark2.4.7,对应的Scala版本是2.11.12;这个依赖会由于Spark内部调用的依赖guava的版本问题出…...

【每日一题Day122】LC1237找出给定方程的正整数解 | 双指针 二分查找
找出给定方程的正整数解【LC1237】 给你一个函数 f(x, y) 和一个目标结果 z,函数公式未知,请你计算方程 f(x,y) z 所有可能的正整数 数对 x 和 y。满足条件的结果数对可以按任意顺序返回。 尽管函数的具体式子未知,但它是单调递增函数&#…...
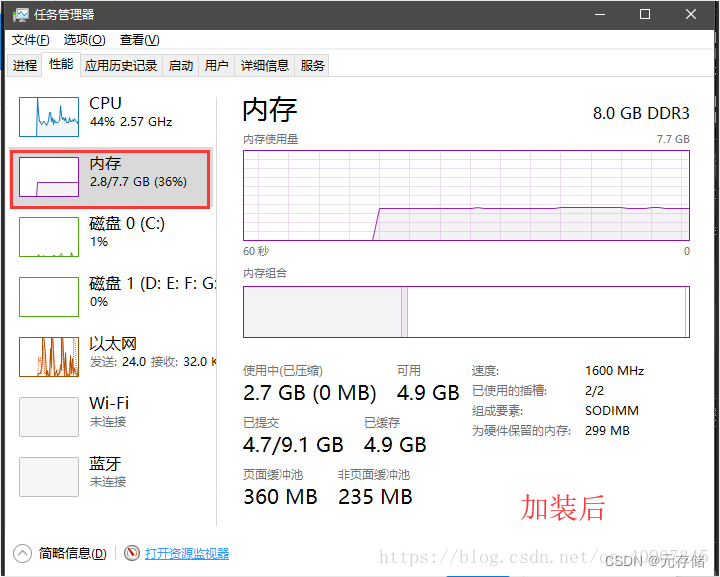
笔记本加装固态和内存条教程(超详细)
由于笔记本是几年前买的了,当时是4000,现在用起来感到卡顿,启动、运行速度特别慢,就决定换个固态硬盘,加个内存条,再给笔记本续命几年。先说一下加固态硬盘SSD的好处:1.启动快 2.读取延迟小 3.写…...

【Python】字典 - Dictionary
字典 - Dictionarykeys()values()items()get()获取文件中指定字符的个数进阶版:获取所有单词的频数进阶版:获取所有字符的频数函数内容keys()输出字典中的所有键values()输出字典中的所有值items()以元组的形式输出键值对get()获取字典中指定键的值 keys…...
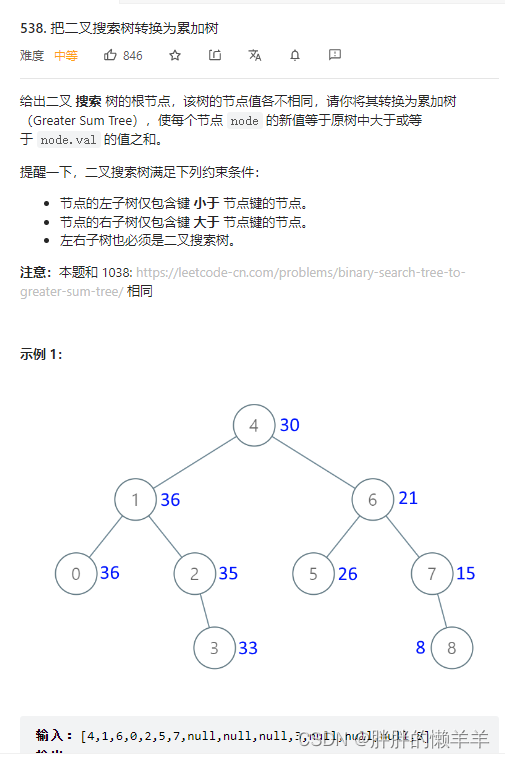
LeetCode分类刷题----二叉树
二叉树1.二叉树的递归遍历144.二叉树的前序遍历145.二叉树的后序遍历94.二叉树的中序遍历2.二叉树的迭代遍历144.二叉树的前序遍历145.二叉树的后序遍历94.二叉树的中序遍历3.二叉树的层序遍历102.二叉树的层序遍历107.二叉树的层序遍历||199.二叉树的右视图637.二叉树的层平均…...
)
Zipkin : Golang 微服务全链路监控(三)
Zipkin : Golang 微服务全链路监控(三) Golang 微服务全链路监控实现 broker-service -> auth-service -> postgres dbzipkin 监控:需代码入侵 使用 zipkin 库的 serverMiddleware,其通过 Http 跟踪(trace&am…...
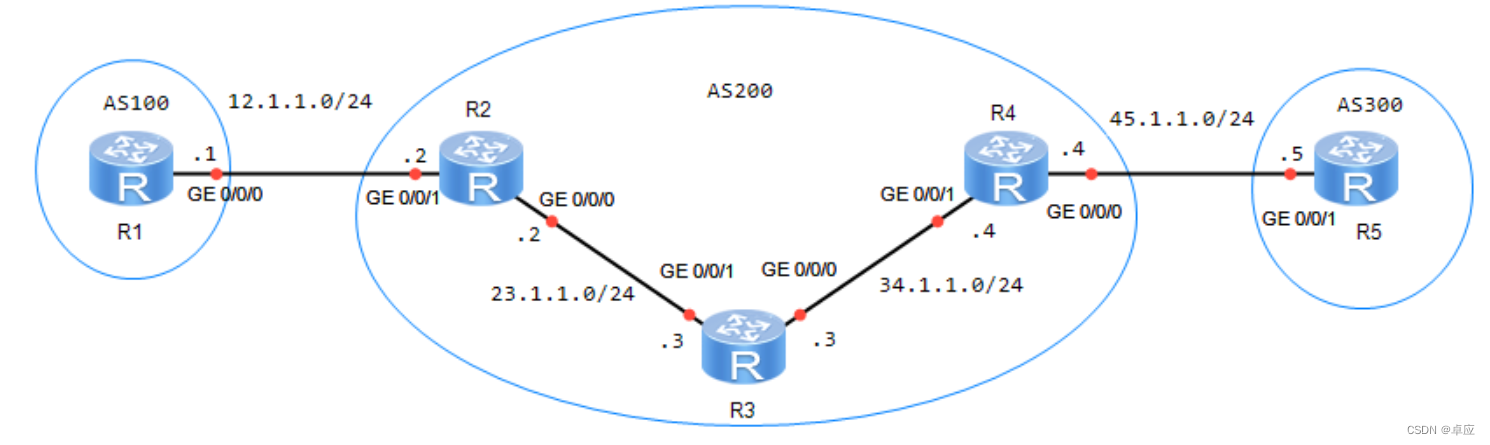
5.3 BGP路由黑洞
5.2.3实验3:BGP路由黑洞 1. 实验目的 熟悉BGP路由黑洞的应用场景掌握BGP水平分割的配置方法2. 实验拓扑 实验拓扑如图5-3所示: 图5-3:BGP路由黑洞 3. 实验步骤 配置IP地址 R1的配置 <Huawei>syst...
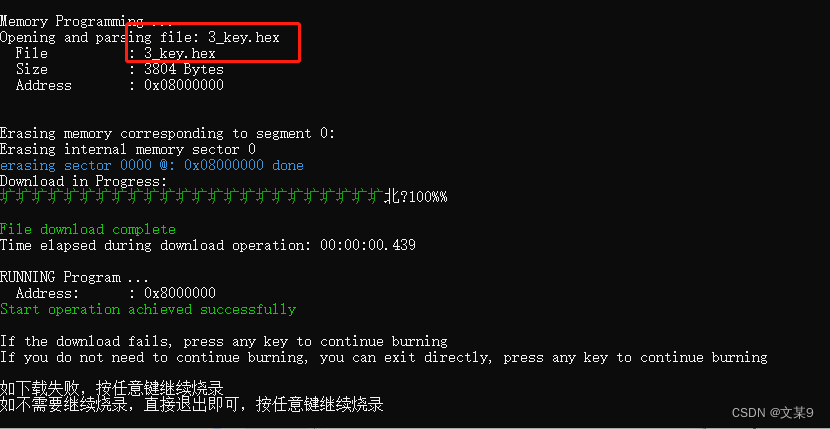
STM32 DFU模式烧录代码
什么是DFU? dfu的本质是isp,usb接口的isp,在系统编程,进入isp的方式我们先了解 如下图 boot0为高电平 boot1为低电平即可进入isp模式。 熟悉的场景 在我们使用flymcu软件下载代码时,本质也是isp 串口接口的isp。 傻瓜使用方式…...
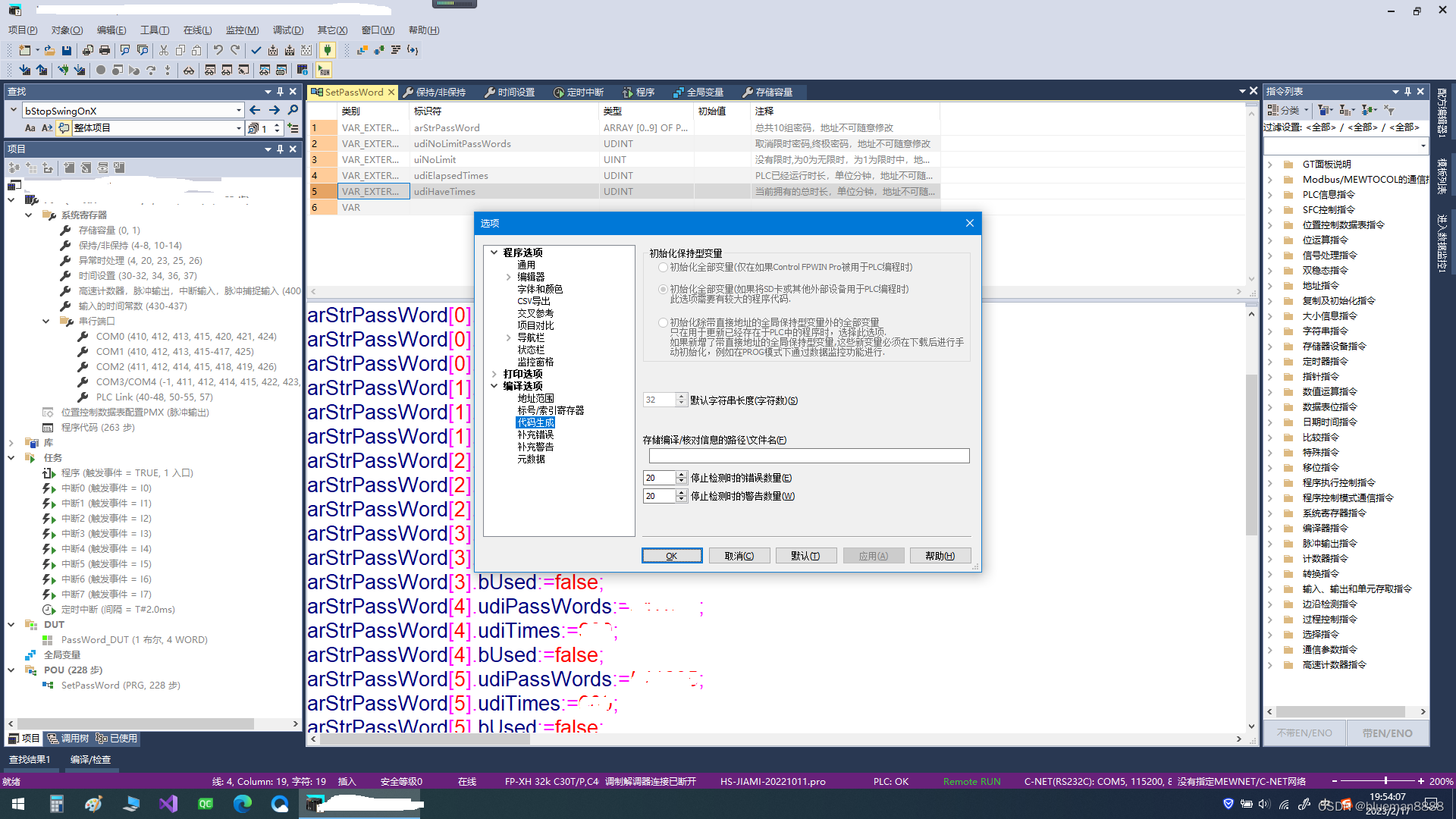
松下PLC通过fpwin上传写入MRTC模块方法
目录 PLC程序上传方法 加密模块使用 PLC程序上传方法 手动将PLC模式设置为prog模式查看PLC是否设置为禁止上传查询指示灯是否变蓝,变蓝则需要将PLC禁止上传功能取消。 3.当上述动作操作完成后,将PLC程序导入到PLC中。为了配合加密程序使用,…...

就业大山之下的网络安全:安逸的安服仔
从去年开始,各个互联网大厂就接二连三的放出了裁员消息,整个互联网行业好像都处于寒冬状态。微博、小米、滴滴、知乎、拼多多等在内的一大批互联网知名企业,也相继传出“人员优化”的消息。 除了国内市场的萧条,国外市场也是不容…...
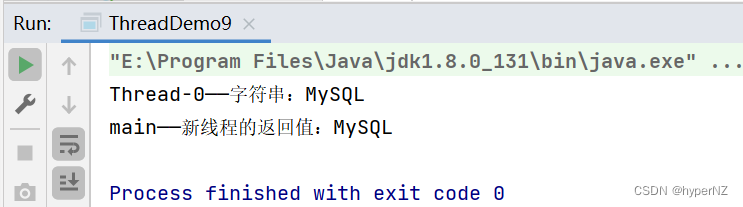
JavaWeb3-线程的3种创建方式7种写法
目录 1.方式一:继承Thread(2种写法) 写法①(常规): a.使用jconsole观察线程 b.启动线程——start方法 PS:(常见面试题)start 方法与 run 方法的区别: 写…...

驱动调试手段
文章目录 前言一、通过sysfs调试LCD查看电源:查看 pwm 信息查看管脚信息总结前言 本文记录在驱动中常用的调试手段 提示:以下是本篇文章正文内容,下面案例可供参考 一、通过sysfs 系统起来之后可以读取 sysfs 一些信息,来协助调试 示例: 调试LCD 输入如下命令 cat /…...

[RK3568 Android12] 音频及路由
1:概述(耳机 ,hdmiin ,板载喇叭) 在开发板上面,系统注册了三个音频输出通道,如下: [ 2.280612] ALSA device list: [ 2.280622] #0: rockchip,rk809-codec [ 2.280630] #1: ROCKCHIP,SPDIF [ 2.280638] #2: rockchip,hdmi console:/proc/asound # cat pcm …...

C++——C++11 第一篇
目录 统一的列表初始化 {}初始化 decltype 编辑 nullptr STL中一些变化 右值引用和移动语义 左值引用和右值引用 总结 左值引用优缺点 右值引用(将亡值) 拷贝赋值和移动赋值 万能引用|完美转发 移动构造和移动赋值注意…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...
