第五十六章 树状数组(一)
第五十六章 树状数组
- 一、前缀和的缺陷
- 二、树状数组
- 1、作用
- 2、算法分析
- 3、算法实现
- (1)lowbits()
- (2)插入
- (3)查询
- 三、例题
- 1、问题
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 2、代码
一、前缀和的缺陷
我们在很久之前介绍过前缀和算法。
我们先来分析一下前缀和算法的优点和缺陷。
这个算法的优点在于能够在O(1)O(1)O(1)的时间复杂度内算出某段区间的和。但是,这个过程的前提是我们没有去修改原数组。也就是说,如果我们在后续过程中修改了原数组中的某个数,我们就必须去修改前缀和数组。
假设我们修改的是原数组中的第一个元素。由于原数组的前nnn项和必定包括第一个元素,所以我们前缀和数组中的每一个元素都需要重新修改。那么这个过程的时间复杂度是O(n)O(n)O(n)的。此时这个前缀和数组相当于没有发挥作用。
总结一下,当我们边修改数组中的某元素边求前缀和的时候,我们原本的前缀和算法就会退化成O(n)O(n)O(n)。
二、树状数组
1、作用
当我们遇到原数组内的元素需要一边修改一边求区间和的时候,就需要用到树状数组。
对于树状数组而言,当修改一个原数组中的元素,我们修改前缀和数组的时候,此时的时间复杂度是O(logn)O(logn)O(logn)。当我们查询某段区间和的时候,时间复杂度也是O(logn)O(logn)O(logn)。
与前缀和算法相比,查询操作从O(1)O(1)O(1)到了O(logn)O(logn)O(logn),修改到操作从O(n)O(n)O(n)到了O(logn)O(logn)O(logn)。
2、算法分析
这个算法解释起来相当麻烦,所以作者这里推荐一个讲解树状数组的视频:
B站:〔manim | 算法 | 数据结构〕 完全理解并深入应用树状数组 | 支持多种动态维护区间操作
3、算法实现
看过上面B站视频的讲解后,我们发现树状数组重要的有三个函数,一个函数是:lowbits(),一个函数是插入,一个函数是查询。
(1)lowbits()
int lowbits(int x)
{return x & -x;
}
(2)插入
void add(int pos, int x)
{for(int i = pos; i <= n; i += lowbits(i))tree[i] += x;return;
}
(3)查询
int quary(int pos)
{int res = 0;for(int i = pos; i; i -= lowbits(i))res += tree[i];return res;
}三、例题
P3374 【模板】树状数组 1
1、问题
题目描述
如题,已知一个数列,你需要进行下面两种操作:
-
将某一个数加上 xxx
-
求出某区间每一个数的和
输入格式
第一行包含两个正整数 n,mn,mn,m,分别表示该数列数字的个数和操作的总个数。
第二行包含 nnn 个用空格分隔的整数,其中第 iii 个数字表示数列第 iii 项的初始值。
接下来 mmm 行每行包含 333 个整数,表示一个操作,具体如下:
-
1 x k含义:将第 xxx 个数加上 kkk -
2 x y含义:输出区间 [x,y][x,y][x,y] 内每个数的和
输出格式
输出包含若干行整数,即为所有操作 222 的结果。
样例 #1
样例输入 #1
5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4
样例输出 #1
14
16
提示
【数据范围】
对于 30%30\%30% 的数据,1≤n≤81 \le n \le 81≤n≤8,1≤m≤101\le m \le 101≤m≤10;
对于 70%70\%70% 的数据,1≤n,m≤1041\le n,m \le 10^41≤n,m≤104;
对于 100%100\%100% 的数据,1≤n,m≤5×1051\le n,m \le 5\times 10^51≤n,m≤5×105。
数据保证对于任意时刻,aaa 的任意子区间(包括长度为 111 和 nnn 的子区间)和均在 [−231,231)[-2^{31}, 2^{31})[−231,231) 范围内。
样例说明:
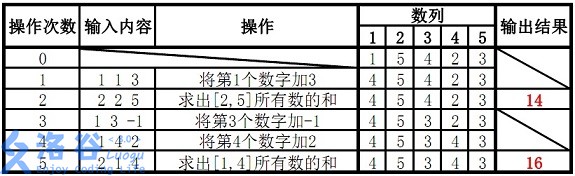
故输出结果14、16
2、代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 5e5 + 10;
int a[N];
ll tree[N];
int n, m;int lowbits(int x)
{return x & -x;
}void add(int pos, int x)
{for(int i = pos; i <= n; i += lowbits(i))tree[i] += x;return;
}ll quary(int pos)
{ll res = 0;for(int i = pos; i; i -= lowbits(i))res += tree[i];return res;
}void solve()
{cin >> n >> m;for(int i = 1; i <= n; i ++ )cin >> a[i];for(int i = 1; i <= n; i ++ )add(i, a[i]);while(m -- ){int op;cin >> op;if(op == 1){int pos ,x;cin >> pos >> x;add(pos, x);}else{int l ,r;cin >> l >> r;cout << quary(r) - quary(l - 1) << endl;}}
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);solve();
}
相关文章:

第五十六章 树状数组(一)
第五十六章 树状数组一、前缀和的缺陷二、树状数组1、作用2、算法分析3、算法实现(1)lowbits()(2)插入(3)查询三、例题1、问题题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1提示2、代码一、前缀和…...
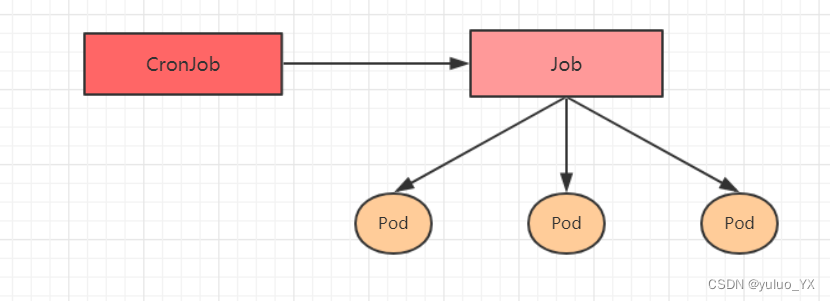
kubernetes教程 --Pod控制器详解
Pod控制器详解 介绍 Pod是kubernetes的最小管理单元,在kubernetes中,按照pod的创建方式可以将其分为两类: 自主式pod:kubernetes直接创建出来的Pod,这种pod删除后就没有了,也不会重建控制器创建的pod&am…...

N2750A Agilent Keysight HP 差分探头1.5GHz
N2750A Agilent Keysight HP 差分探头13554860890 N2750A 是 Agilent Keysight HP 的 1.5 GHz 差分探头。 特征: N2750A:1.5 GHz 衰减比:2:1 或 10:1(可切换) 动态范围: 5 V 或 10 Vpp(10:1 时…...

一文搞懂Linux内核进程CPU调度基本原理
为什么需要调度 进程调度的概念比较简单,我们假设在一个单核处理器的系统中,同一时刻只有一个进程可以拥有处理器资源,那么其他的进程只能在就绪队列中等待,等到处理器空闲之后才有计划获得处理器资源来运行。在这种场景下&#…...
java ssm爱宠宠物医院挂号预约系统管理系统设计与实现
本课题所实现的宠物医院网站是基于网页,它可以实现网上预约挂号,评价等基本功能。用户只要手边有一部手机或者一台电脑,可以上网浏览网页,便可以使用本系统,没有时间和地点的限制,使得就医预约,…...
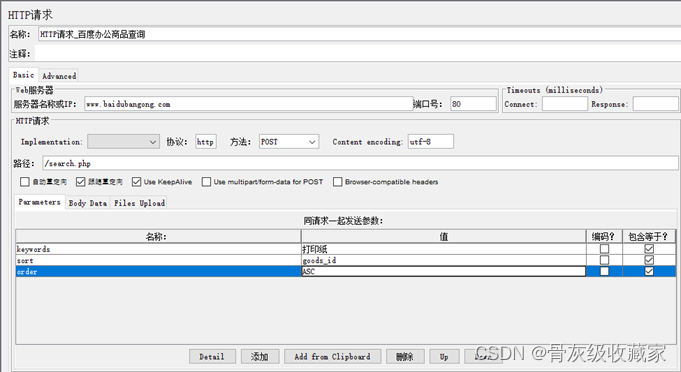
自动化测试工具_Jmeter
【课程简介】 接口测试是测试系统组件间接口的一种测试,接口测试天生为高复杂性的平台带来高效的缺陷监测和质量监督能力,平台越复杂,系统越庞大,接口测试的效果越明显。在接口测试大行其道的今天,测试工具也愈发重要,Jmeter作为一款纯 Java 开发的测试…...

不是所有人都适合职场
一个读者的提问: 洋哥,我目前工作五年在一家大厂,属于那种什么事情上手都很快的人,并且搞定新问题能产生沉浸般的快感。我的本职是程序员,但运营思路产品方法也都会一些,甚至有时候提出的方案效果比产品&a…...
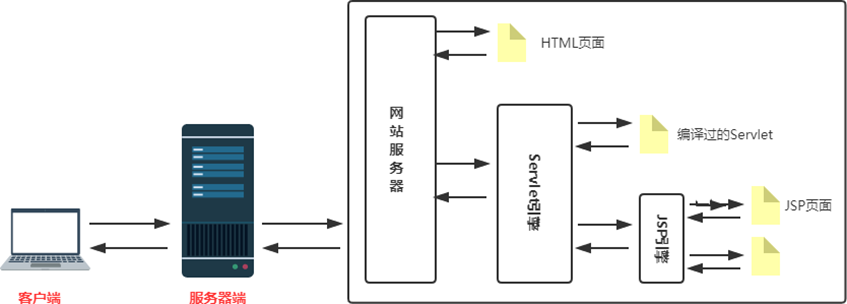
JSP 和 JSTL
文章目录🍓摘要🍓一、JSP🍉1.1 JSP的基础语法🍫1.1.1 简介🍫1.1.2 依赖🍫1.1.3 注释🍫1.1.4 Scriptlet 脚本🍉1.2 JSP的指令标签🍫1.2.1 include 静态包含🍫1…...

数据分析| Pandas200道练习题,使用Pandas连接MySQL数据库
文章目录使用Pandas连接数据库编码环境依赖包read_sql_query()的使用read_sql_table()的使用read_sql() 函数的使用to_sql()写入数据库的操作删除操作更新操作总结:使用Pandas连接数据库 通过pandas实现数据库的读,写操作时,首先需要进行数据…...

【Node.js】全局可用变量、函数和对象
文章目录前言_dirname和_filename变量全局函数setTimeout(cb,ms)clearTimeout(t)setInterval(cb,ms)clearInterval(t)setImmediate(cb)clearImmediate()console对象console.info([data][,...])console.error([data][,...])console.warn([data][,...])console.dir(obj[,options]…...

package.json 开发依赖与运行时依赖
文章目录前言一、生产环境与开发环境二、dependencies二、devDependencies总结前言 我已经使用npm接近两年了, 但对于package.json内的dependencies 和devDependencies也只是知道什么依赖该放什么部分, 至于为什么放到这个部分, 我不是很了解… 呃, 还是去了解一下. 一、生产环…...

关于最短路径算法中边的权值的思考
关于最短路径算法中边的权值的思考 不管是单源最短路径算法:Dijkstra Bellman-ford 还是多源最短路径算法:floyed Johnson 我们都绕不开的一件事就是,边的权值wi,jw_{i,j}wi,j 下面我们从多个角度谈边的权值 1.权值恒定 它是指对于每条边…...
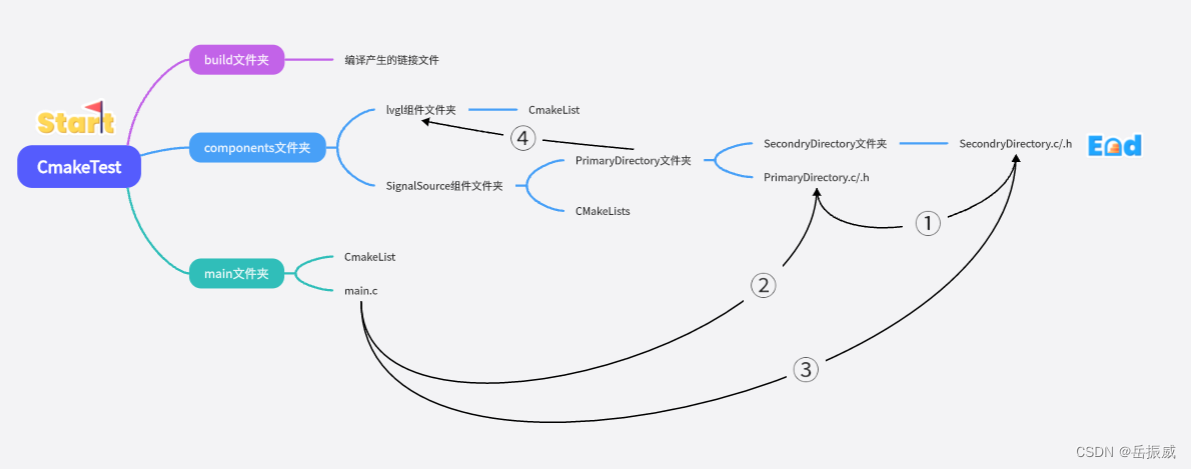
LVGL开发教程:二、ESP-IDF 使用CmakeList管理自己的文件以及文件夹
本文需要已经安装了Vscode+IDF插件没有安装的请提前安装一下,IDF插件为乐鑫的插件不需要翻墙。需要环境搭建请看下面链接。 环境搭建: VScode+platformIO和Vscode+ESP-IDF两种开发环境搭建 项目例程下载地址: IDF-CmakeTes,密码:8888 另外,由于你和我的路径不一致,下载的工…...

与感受野相关的几种网络结构
一、Inception 1. Inception v1 目的 通过设计一个稀疏网络结构,但是能够产生稠密的数据,既能增加神经网络表现,又能保证计算资源的使用效率。 结构 图1-1 Inception v1结构图 特点 共4个通道,其中3个卷积通道分别使用111111…...
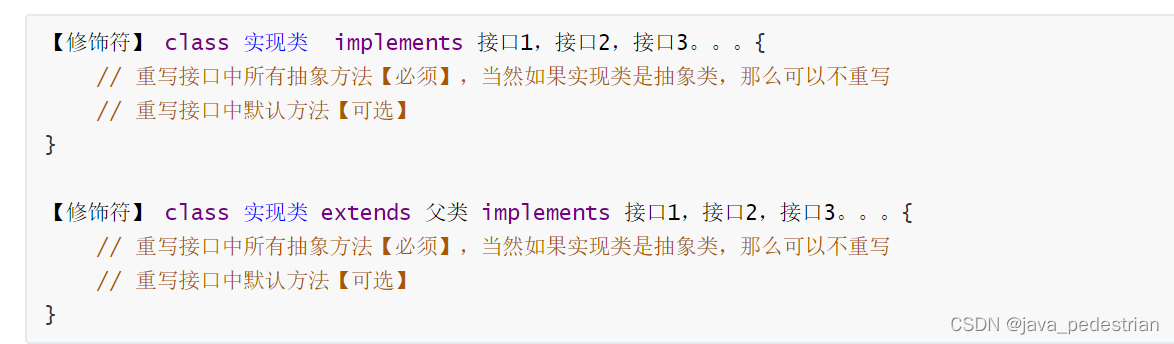
day19_抽象类丶接口
由来 当我们声明一个几何图形类:圆、矩形、三角形类等,发现这些类都有共同特征:求面积、求周长、获取图形详细信息。那么这些共同特征应该抽取到一个公共父类中。但是这些方法在父类中又无法给出具体的实现,而是应该交给子类各自…...

【网安神器篇】——系统指纹探测工具finger
作者名:白昼安全主页面链接: 主页传送门创作初心: 以后赚大钱座右铭: 不要让时代的悲哀成为你的悲哀专研方向: web安全,后渗透技术每日鸡汤: 我不想停下,因为这次出发的感觉太好了一…...
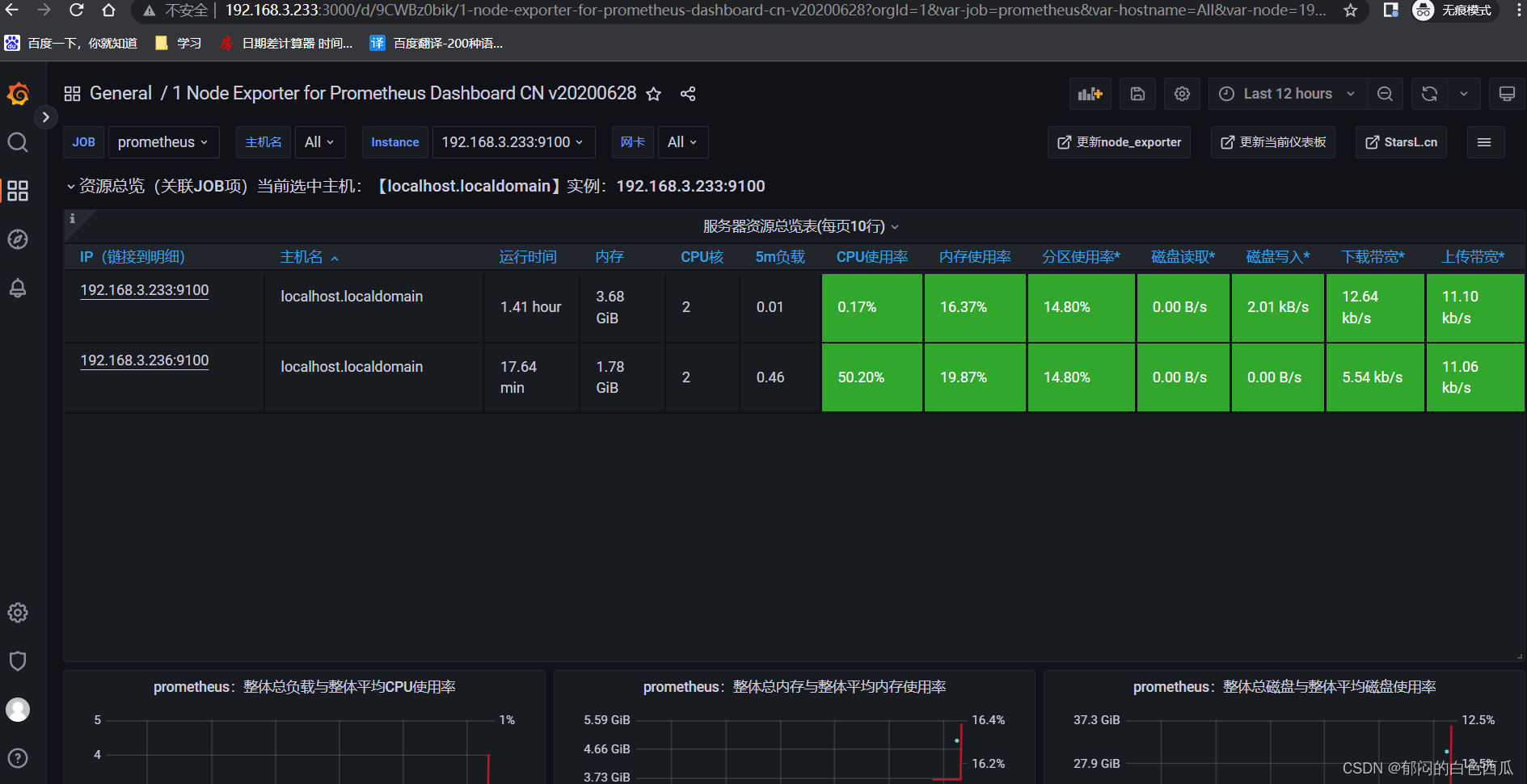
Prometheus离线tar包安装
Prometheus离线tar包安装实验环境一、部署前操作二、Master2.1下载2.2解压2.3更改服务目录名称2.4创建系统服务启动文件2.5配置修改2.6启动并设置开机自启2.7访问2.8添加node节点2.8.1 添加方法2.8.2修改Prometheus配置(Master)————————————…...
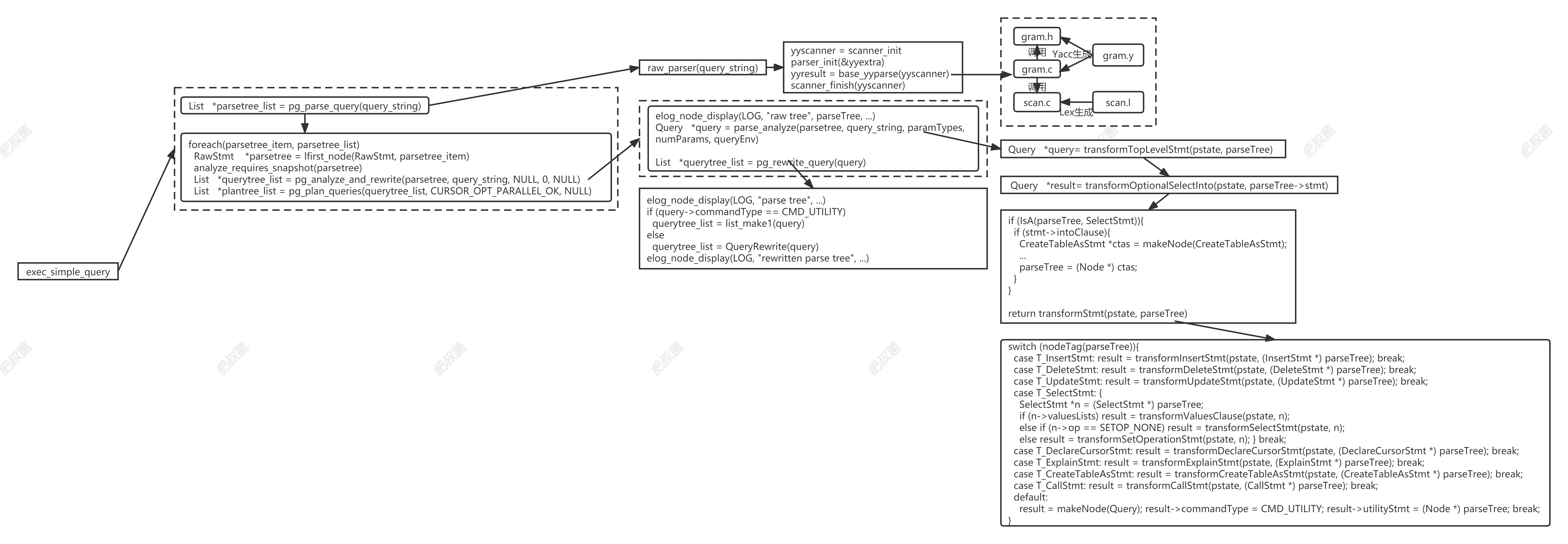
PostgreSQL查询引擎——SELECT STATEMENTS SelectStmt
SelectStmt: select_no_parens %prec UMINUS| select_with_parens %prec UMINUS select_with_parens:( select_no_parens ) { $$ $2; }| ( select_with_parens ) { $$ $2; } 该规则返回单个SelectStmt节点或它们的树,表示集合操作树(set-operation tree…...
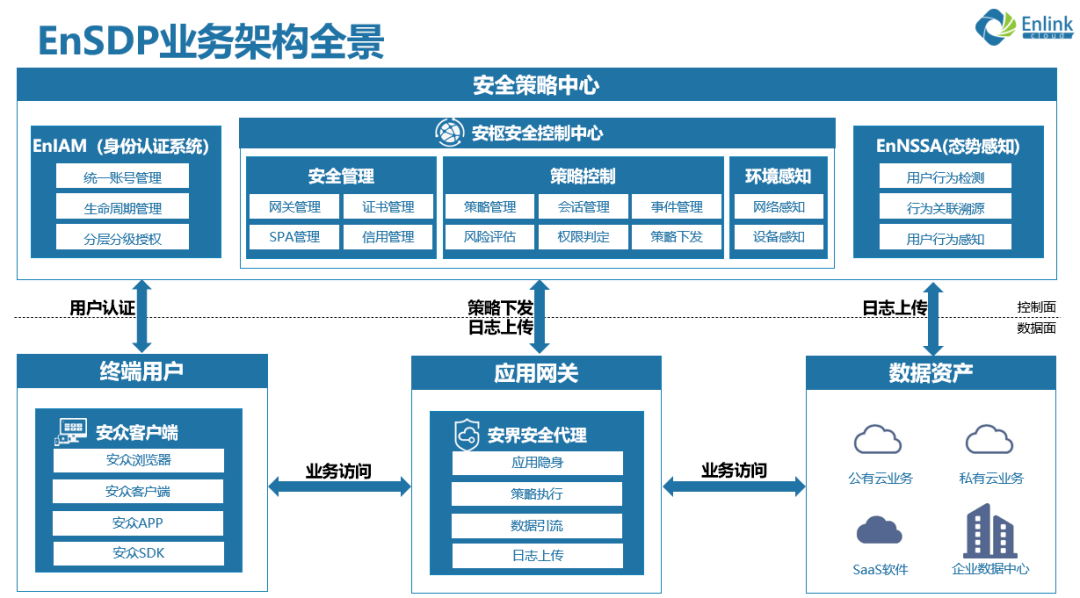
零信任-易安联零信任介绍(11)
目录 易安联零信任公司介绍 易安联零信任发展路线 易安联零信任产品介绍 易安联零信任架构 易安联零信任解决方案 易安联零信任发展展望 易安联零信任公司介绍 易安联是一家专业从事网络信息安全产品研发与销售,是行业内领先的“零信任”解决方案提供商&…...

C++ STL——map和set的使用
文章目录1. 关联式容器1.1 键值对1.2 树形结构的关联式容器2. set2.1 set的介绍2.2 set的插入2.3 set的删除和查找2.4 lower_bound和upper_bound3. multiset3.1 count4. map4.1 map的介绍4.2 map的插入4.3 map的遍历4.4 map的[ ]5. multimap1. 关联式容器 我们之前学的vector、…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...
