机器学习笔记
一
1.类型
有监督:分类、回归
无监督:聚类、降维
2.挑战:
过拟合:泛化能力弱
欠拟合:模型过于简单
二、
1.开发流程
数据收集->数据清洗->特征工程->数据建模
2.选择性能指标:
回归问题 均方根误差rmse

平均绝对误差 mae

rmse 对异常值更加敏感
3.寻找相关性
区间是-1 到 1,靠近0为没有线性相关性
4.数据清理
处理缺失值
5.处理文本和分类属性
将文本转到数字;
有序类别:“坏”“好”“平均”等
无序类别:创建独热向量
6.特征缩放
目标值不缩放,同比例缩放所有属性的两种常用方法是最大最小缩放(归一化)和标准化
7.归一
将值重新缩放使其最终范围在0~1间
实现方法是将值减去最小值并除以最大值和最小值的差
提供转化器
8.标准
首先减去平均值(所以标准化值的均值总是零),然后除以方差,从而使得结果的分布具备单位方差。
标准化不将数值绑定到特定范围。
受异常值影响更小
9.k-折交叉验证
防止过拟合,在训练数据中分出一部分作为验证数据
它将训练集随机分割成k个不同的子集,每个子集称为一个折叠,然后对模型进行k次训练和评估——每次挑选1个折叠进行评估,使用另外的k-1个折叠进行训练。产生的结果是k次评估分数
三、
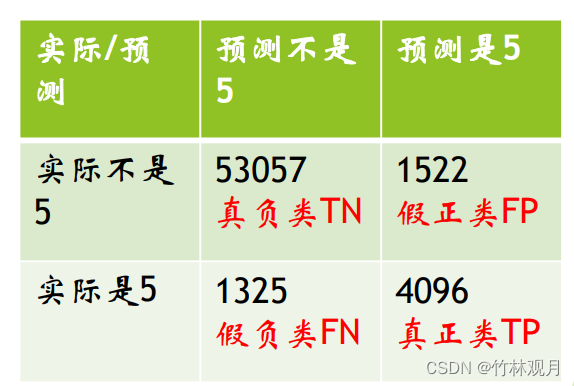
1.混淆矩阵
行表示实际类别,列表示预测类别
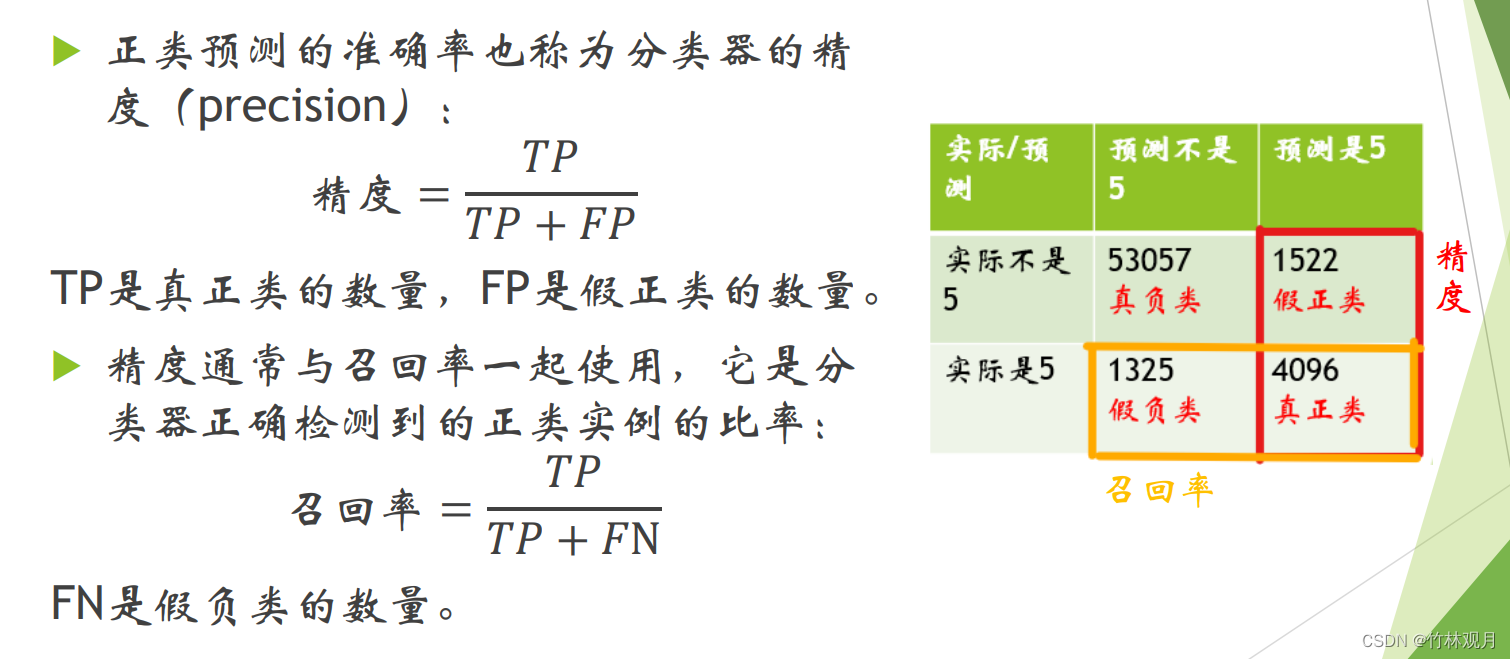
2.精度与召回率
预测与实际相符就是真
预测正面为正
正类预测的准确率是精度:真正占正类的概率
正确检测到的正类实例的比率是召回率:
| 预测不是 | 预测是 | |
|---|---|---|
| 实际不是 | 真负 | 假正 |
| 实际是 | 假负 | 真正 |
3.F1分数
F1=21精度+1召回率F_1=\frac{2}{{\frac{1}{精度}}+{\frac{1}{召回率}}}F1=精度1+召回率12
F1分数是精度和召回率的谐波(harmonic mean)平均值。
正常的平均值平等对待所有的值,而谐波平均值会给予低值更高的权重。因此,只有当召回率和精度都很高时,分类器才能得到较高的F1分数
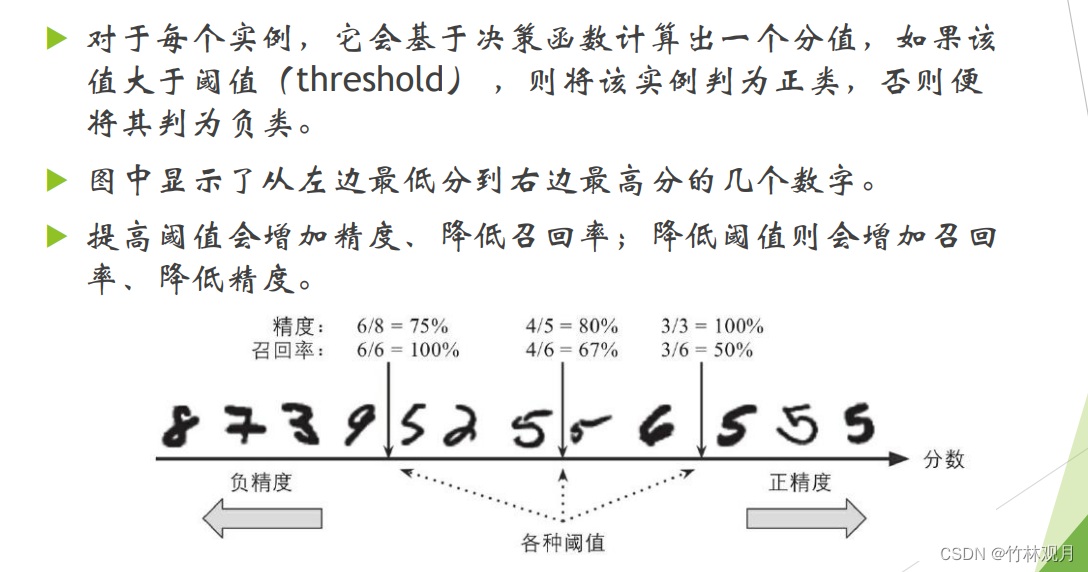
4.精度/召回率权衡
基于决策函数计算出一个分值,高于他为正
5.roc曲线
绘制的真正类率和假正类率
虚线表示春随机分类器的ROC曲线、优秀的分类器应该远离该曲线(向左上角)
比较方法:测量曲线下面积(AUC)完美的分类器ROC AUC 等于1,纯随机等于0.5
四、
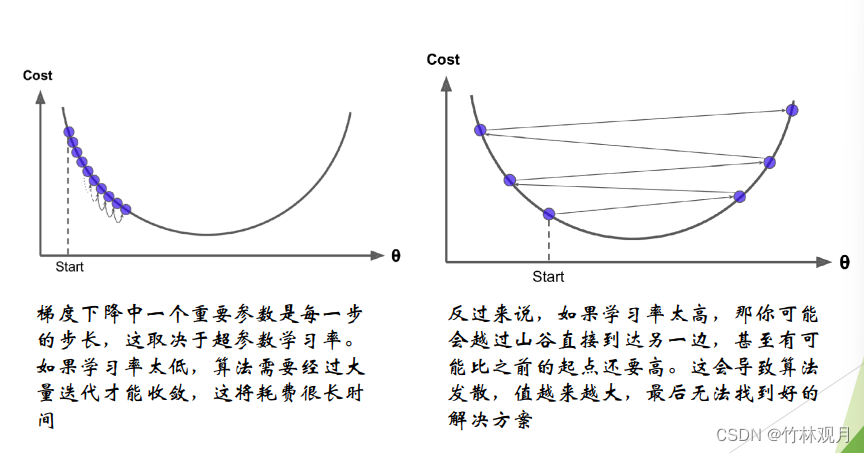
1.梯度下降
优化算法,能够为大范围的问题找到最优解。中心思想:迭代地调整参数从而是成本函数最小化。
调整参数向量相关的误差函数的局部梯度,并不断沿着降低梯度的方向调整直到梯度降为零,达到最小值。
先使用一个随机的θ,然后逐步改进,知道收敛出一个最小值
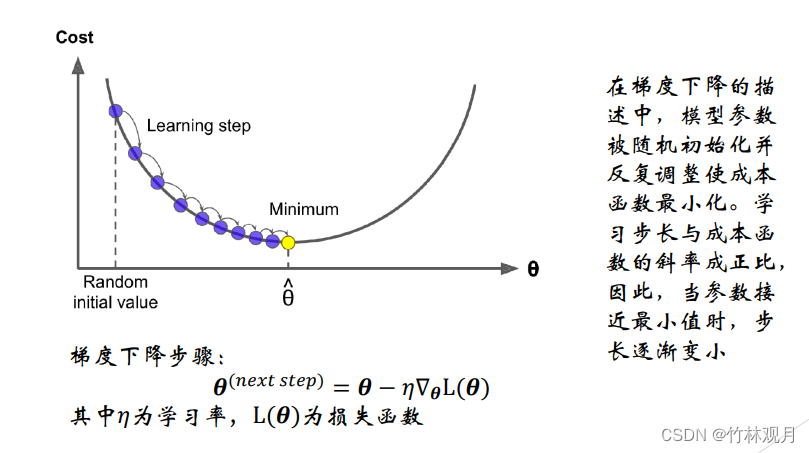
学习率太高太低
应用梯度下降时,需要保证所有特征值的大小比例都差不多
2.随机梯度下降
随机性的好处在于可以逃离局部最优,缺点是定位不出最小值。
解决方法:逐步降低学习率。开始的步长大然后越来越小。叫做:模拟退火
确定每个迭代学习率的函数叫作学习率调度。
学习率降的太快:可能会陷入局部最小值,甚至是停留在走向最小值的半途中。
太慢:需要太长时间才能跳到差不多最小值附近,如果提早结束训练,可能只得到一个次优的解决方案
3.多项式回归
可以使用线性模型来拟合非线性数据,一个简单的方法就是将每个特征的幂次方添加为一个新特征,然后在此扩展特征集上训练一个线性模型

4.学习曲线
用来估计模型的泛化性能:该曲线绘制的是模型在训练集和验证集上关于训练集大小(或训练迭代)的性能函数
要生成这个曲线,只需要在不同大小的训练子集上多次训练模型即可
5.代码实现
当训练集中只有一个或两个实例时,模型可以很好地拟合它们。随着将新实例添加到训练集中,模型不可能完美拟合。因为有噪声和他不是线性的,训练数据上的误差会一直上升到平稳的状态。
训练模型时,无法正确泛化,最初验证误差很大,经历更多的训练示例,开始学习,验证错误逐渐降低。误差最终达
到一个平稳的状态,非常接近另外一条曲线
与线性回归模型相比,训练时据上的误差会小很多。
曲线之间存在间隙。这意味着该模型在训练数据上的性能要比在验证数据上的性能好得多,这是过拟合模型的标志。如果使用更大的训练集,则两条曲线会继续接近
6.正则化线性模型
减少过拟合的一个好方法是对模型进行正则化(即约束模型):它拥有的自由度越少,则过拟合数据的难度就越大。
包括岭回归,Lasso回归,弹性网络
7.岭回归
成本函数:
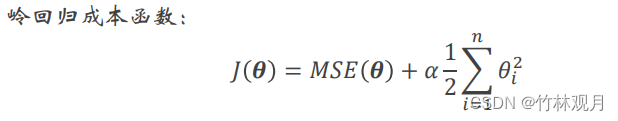
将正则化项添加到成本函数,迫使学习算法不仅拟合数据,而且还使模型权重尽可能小
超参数α控制要对模型进行正则化的程度。如果α=0,则岭回归仅是线性回归。如果α非常大,则所有权重最终都非常接近于零,结果是一条经过数据均值的平线
偏置项𝜃0没有进行正则化
在执行岭回归之前缩放数据(例如使用StandardScaler)很重要,因为它对输入特征的缩放敏感。大多数正则化模型都需要如此
8.Lasso回归
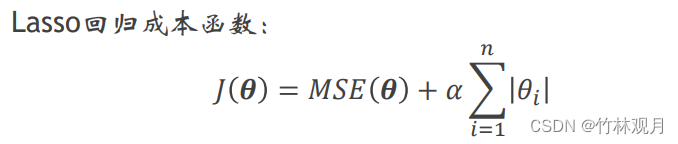
线性回归的另一种正则化叫作最小绝对收缩和选择算子回归
Lasso回归的一个重要特点是它倾向于完全消除掉最不重要特征的权重
7.逻辑回归
被广泛用于估算一个实例属于某个特定类别的概率,是一个二元分类器。
模型:
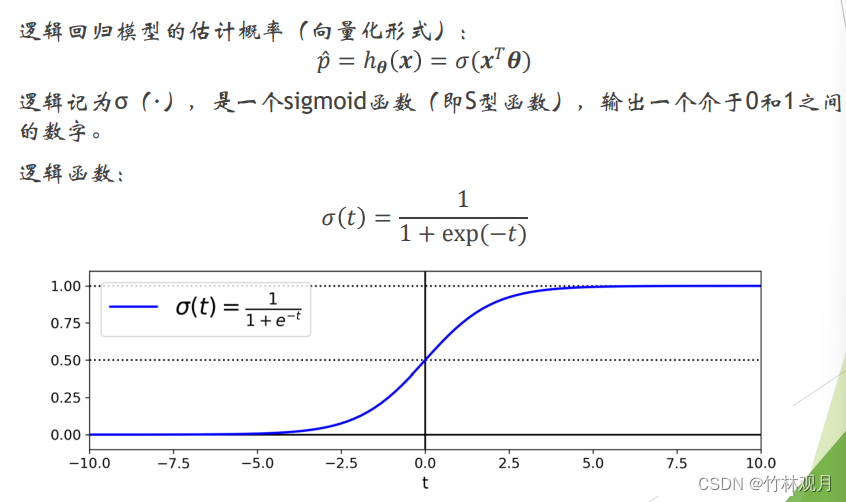
说出介于0和1之间
预测:
估算出实例x属于正类的概率𝑝= ℎ𝜽(𝒙),就可以做出预测𝑦

8.Softmax回归
经过推广,可以支持多个类别,且不需要训练并组合多个二元分类器
给定一个实例x,Softmax回归模型首先计算出每个类k的分数𝑠𝑘(𝑥),然后对这些分数应用softmax函数(也叫归一化指数),估算出每个类的概率
五、
1.硬间隔支持向量机
2.非线性支持向量机
六、
决策树模型
1.分类树、回归树
2.基本思想:减少不缺定性
3.度量不确定性的指标:
分类错误率
熵:

基尼指数:

4.结束划分:
预设或无法再分
七、
1.bagging
给定一个训练集,基于自助采样法采样出T个含有m个训练样本的采样集;
基于采样机训练一个基学习器,将这些基学习器进行结合;
每个预测器使用费的算法相同,当时在不同的训练集随机子集上进行训练
2.boosting
增加前一个基学习器在训练过程中预测错误样本的权重,使得后续基学习器更加关注这些打标错误的训练样本,尽可能纠正这些错误,一直向下串行直至产生需要的T个基学习器,Boosting最终对这T个学习器进行加权结合,产生集成学习器。
特点:串行 序列化
3.区别
样本选择:
bagging:训练集在原始集是有放回选取的
boosting:每一轮的训练集不变,只是每个样例的权重发生变化
样例权重:
bagging:权重相等
boosting:根据失误率不服按调整样例的权值,错误率越大权重越大
预测函数:
bagging:所有预测函数的权重相等
boosting:每个弱分类器都有对应的权重,对于分类误差小的分类器权重更大
并行计算:
bagging:可以并行
boosting:只能顺序生成
九、
1.主成分分析
需要找到一种合理的方法,在减少需要分析的指标同时,尽量减少原指标包含信息的损失,以达到对所收集数据进行全面分析的目的。
由于各变量之间存在一定的相关关系,因此可以考虑将关系紧密的变量变成尽可能少的新变量,使这些新变量是两两不相关的,那么就可以用较少的综合指标分别代表存在于各个变量中的各类信息。
降维算法
2.概念
PCA的主要思想是将n维特征映射到k维上,这k维是全新的正交特征也被称为主成分,是在原有n维特征的基础上重新构造出来的k维特征。
PCA的工作就是从原始的空间中顺序地找一组相互正交的坐标轴,新的坐标轴的选择与数据本身是密切相关的。
第一个新坐标轴选择是原始数据中方差最大的方向,第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的,第三个轴是与第1,2个轴正交的平面中方差最大的。依次类推,可以得到n个这样的坐标轴。
通过这种方式获得的新的坐标轴,我们发现,大部分方差都包含在前面k个坐标轴中,后面的坐标轴所含的方差几乎为0。
于是,我们可以忽略余下的坐标轴,只保留前面k个含有绝大部分方差的坐标轴。
3.基于特征值分解协方差矩阵实现PCA算法

相关文章:

机器学习笔记
一 1.类型 有监督:分类、回归 无监督:聚类、降维 2.挑战: 过拟合:泛化能力弱 欠拟合:模型过于简单 二、 1.开发流程 数据收集->数据清洗->特征工程->数据建模 2.选择性能指标: 回归问题 均方根…...
L1-072 刮刮彩票
“刮刮彩票”是一款网络游戏里面的一个小游戏。如图所示: 每次游戏玩家会拿到一张彩票,上面会有 9 个数字,分别为数字 1 到数字 9,数字各不重复,并以 33 的“九宫格”形式排布在彩票上。 在游戏开始时能看见一个位置上…...
)
互联网摸鱼日报(2023-02-18)
互联网摸鱼日报(2023-02-18) InfoQ 热门话题 从用云焦虑到“深度云化”,新云原生时代带给我们哪些思考? 数据治理之需求层次 GitHub 更新 Copilot 以阻止不安全代码,并称其支持了超 60% 的 Java 开发者 数据库隔离…...
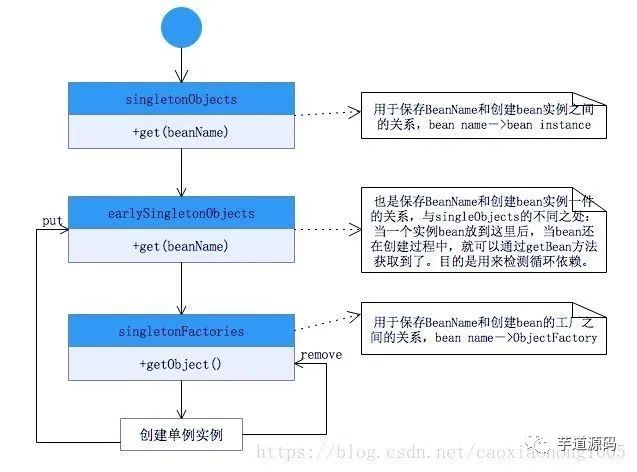
Spring 中经典的 9 种设计模式
1.简单工厂(非23种设计模式中的一种) 2.工厂方法 3.单例模式 4.适配器模式 5.装饰器模式 6.代理模式 7.观察者模式 8.策略模式 9.模版方法模式 Spring中涉及的设计模式总结 1.简单工厂(非23种设计模式中的一种) 实现方式: BeanFactory。Spring中的BeanFa…...

CentOS7突然没法上网【Network 中wired 图标消失】
参考文章(七种办法):CentOS 7 右上角网络连接图标消失,设置网络有线消失解决办法 正常图标消失,先在 终端命令 依次执行以下命令 service NetworkManager stop service network restart service NetworkManager start 一、问题真烦 CentOS7图形化界面安装…...
SpringBoot3集成TDengine自适应裂变存储
前言 首先很遗憾的告诉大家,今天这篇分享要关注才可以看了。原因是穷啊,现在基本都是要人民币玩家了,就比如chatGPT、copilot,这些AI虽然都是可以很好的辅助编码,但是都是要钱。入驻CSDN有些年头了,中间有几…...

golang alpine 配置gstreamer开发环境
启动容器 sudo docker run -it --name golang -v $PWD:/home/leon -d golang:1.18-alpine3.17tar zxvf x86_64-linux-musl-cross.tgz mv x86_64-linux-musl-cross /usr/local/musl export PATH$PATH:/usr/local/musl/bin/:/usr/local/musl/x86_64-linux-musl/bin 下载gstre…...

SAP ABAP GUI_DOWNLOAD中下载乱码的问题
1 GUI_DOWNLOAD 1.1 问题表现 GUI_DOWNLOAD在应用当中有时会导致输出的文件在某些电脑正常显示,在某些电脑乱码显示。这个固然是由于各个电脑系统配置有差异,但是我们可以在应用该函数时就排除该差异来保证任意台电脑正常显示输出的文件。 如下…...
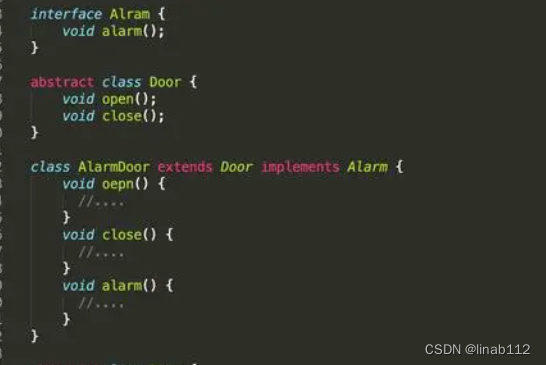
接口和抽象类
接口(Interface)和抽象类(Abstract Class)是支持抽象类定义的两种机制。 1.抽象类 (1)说明 在Java中被abstract关键字修饰的类称为抽象类,被abstract关键字修饰的方法称为抽象方法,抽象方法只有方法的声明,没有方法体。抽象类是用来捕捉子…...

ES7新特性
1. ES7 新特性 1.1. Array.prototype.includes includes 方法用来检测是否包含某个数组,返回布尔类型值 其他检测包含字符串的方法: indexOf(),返回的是下标值,如果没有则返回-1 1.2 指数操作符 指数…...
【软件测试】资深测试总结的几个自动化测试点,提升跨越一大步......
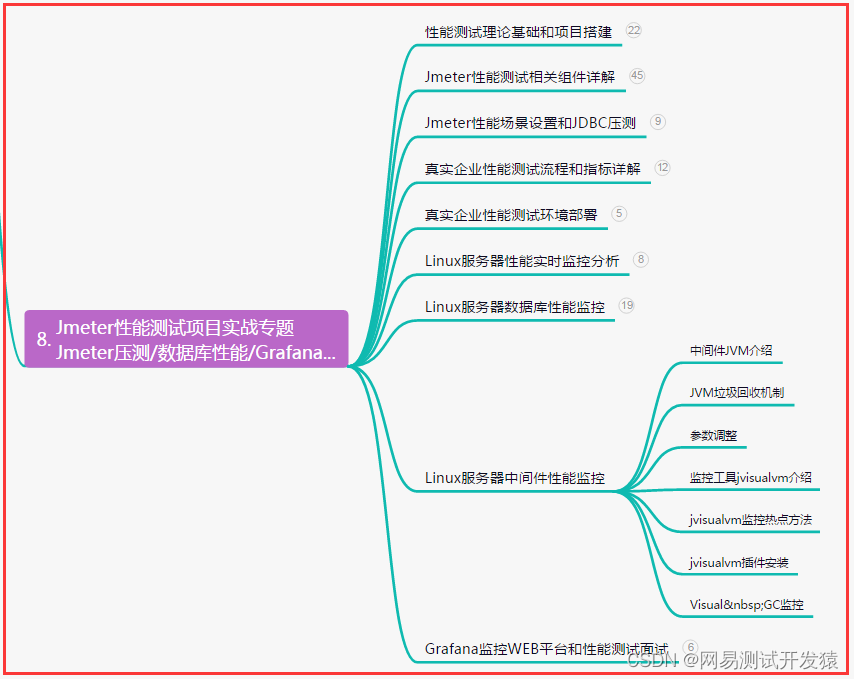
目录:导读前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜)前言 自动化的软件测试与…...
)
GEE:时间序列分析1——认识arraySlice()
本文是记录时间序列分析系列教程的开篇之作,教程由浅入深介绍在GEE平台上进行时间序列分析的方法和代码。本教程会从操作时间序列的基本函数开始讲解,到后续更新会加入一些成熟的时间序列分析方法。随着本教程文章数量增加到一定数量,本专栏会适当涨价。欢迎乐多们订阅。 文…...
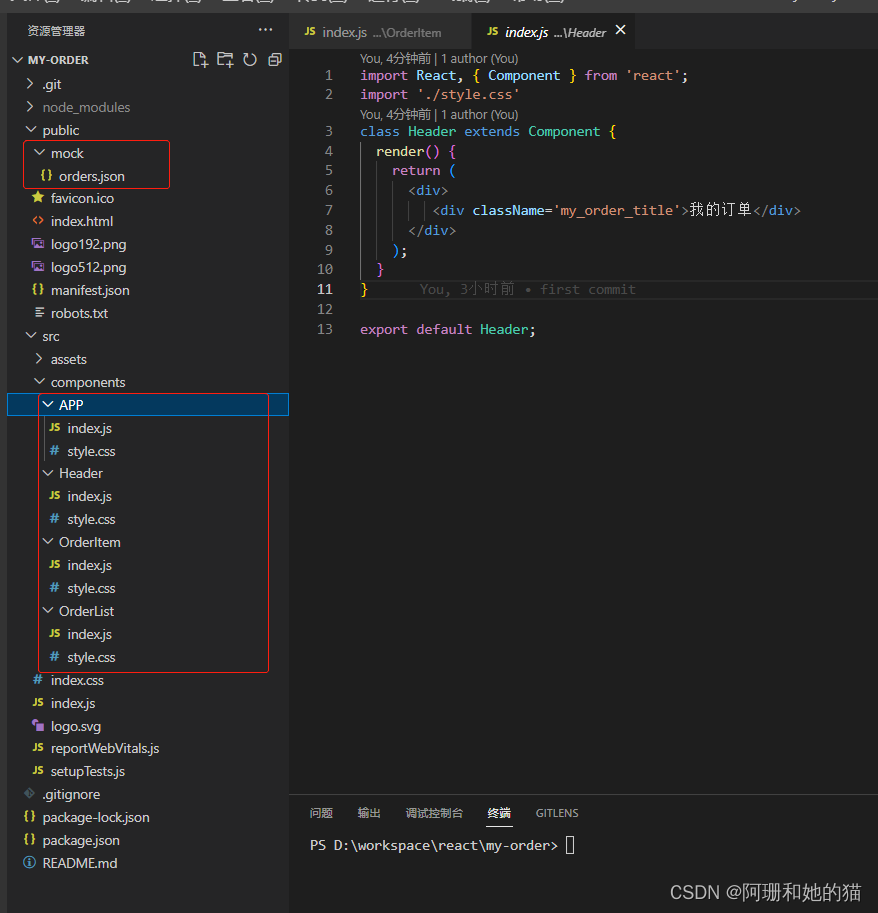
【react实战小项目:笔记】用React 16写了个订单页面
视频地址 React 16 实现订单列表及评价功能 简介:React 以其组件化的思想在前端领域大放异彩,但其革命化的前端开发理念对很多 React 初学者来说, 却很难真正理解和应用到真实项目中。本课程面向掌握了 React 基础知识但缺乏实战经验的开发…...

30岁+的人如何进行自我提升和职场规划
今天非常忙一天开了N个会,一堆头疼的事情要解决,一晃就加班到现在,刚打到了的士开始想今天分享点什么。 实在不知道写什么了,突然想起下午部门茶话会小伙伴问的问题:“30岁的人如何进行自我提升和职场规划”。 这是个…...
创建基于Vue2.0开发项目的两种方式
前天开始接触基于Vue2.0的前端项目,实际操作中肯定会遇到一些问题,慢慢摸索和总结。 其实,作为开发一般企事业单位应用的小项目,前端的懂一点HTMLCSSJavaScroptJQueryJson(或者Xml),后端懂一…...

[测试]性能测试
最近遇到一个性能测试的问题,虽然最后确定是一个乌龙问题。这里还是总结一下,看是否有可以从中学到什么。 场景: 月底要出一个新版本。测试人员发现这个新版本在相同的负载的情况下,会有队列使用负荷过高的警告。之前的版本没有。…...
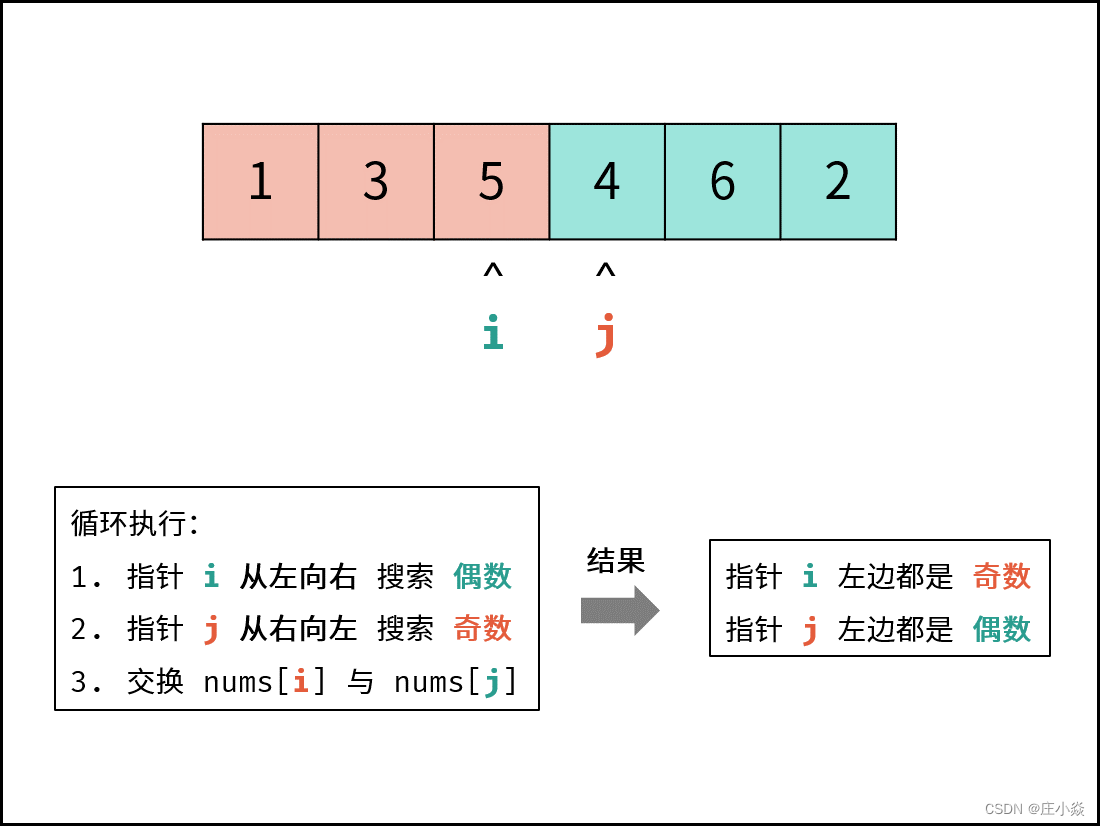
剑指 Offer 21. 调整数组顺序使奇数位于偶数前面
摘要 剑指 Offer 21. 调整数组顺序使奇数位于偶数前面 一、双指针解析 考虑定义双指针 i , j分列数组左右两端,循环执行: 指针 i从左向右寻找偶数;指针 j从右向左寻找奇数;将偶数nums[i]和奇数 nums[j]交换。 可始终保证&…...
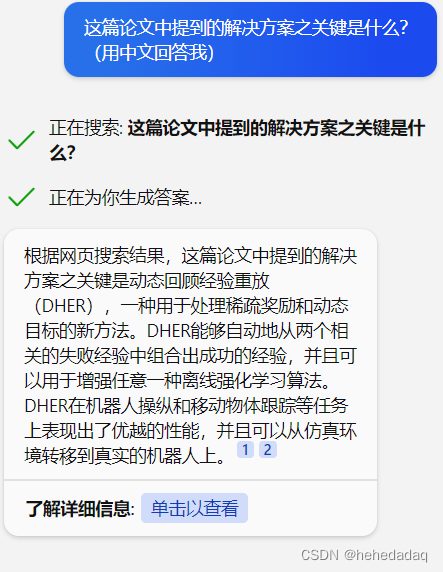
实用版ChatBing论文阅读助手教程+新测评
实用版ChatBing论文阅读助手新测评 AI进化(更新)的速度太快了!距离我上次的【Chat嘴硬!基于NewBing的论文调研评测报告】,才四天,它已经进化到快能用的地步了! 这次是我刷B站看到热门推荐&…...
Linux生产者消费模型
1.生产者消费者模型 1.1 为何要使用生产者消费者模型 生产者消费者模式就是通过一个容器来解决生产者和消费者的强耦合问题。生产者和消费者彼此之间不直接通讯,而通过阻塞队列来进行通讯,所以生产者生产完数据之后不用等待消费者处理,直接…...
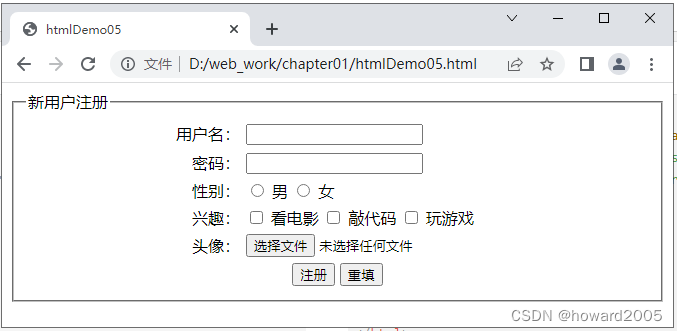
动态网站开发讲课笔记01:网页开发基础
文章目录零、本讲学习目标一、HTML基础(一)HTML简介1、HTML2、HTML语言的基本格式3、<!DOCTYPE>声明4、html标签5、head标签6、body标签7、编写第一个网页8、关于编写HTML文件的工具9、HTML标签概述(1)单标签(2&…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...
