15个顶级思维模型
今天给大家分享几个思维模型,无论是数分、数开还是其他岗位,都会有所启发。
查理·芒格认为,每个学科都是从一个独特的角度去切入了解这个世界,都是一个摸象的瞎子。
要超越普通人的认知决策,就必须掌握多个核心思维模型。
以下内容是从查理·芒格的100种思维模型中提炼出的15个,让人受益终身。如果看完觉得有点东西,欢迎分享给更多人~
01 非线性思维
由于人类长期的进化结果,我们更倾向于用“线性”思维方式理解世界。
然而,世界的本质是非线性的。这个世界之所以有些人能取得巨大成功,而大部分人平平凡凡,关键于他们的思维方式是线性的还是非线性的。
非线性思维的核心:
- 理解世界是非线性、跳跃发展、不可精确预测的;
- 理解引起质变的核心原因,加速或者等待临界点的来临,获取质变期的巨大收益;
- 在积累期勇于放弃短期利益,做能够对促进上一条有益的事情(如在积累期投入更多本金、积累更多的工作经验等)。
非线性思维方式具有系统辩证思维、发散思维、逆向思维、直觉思维和灵感思维五种基本形式。
02 黄金圈思维
黄金圈是认知世界的方式,有三个层面。从why出发,探究问题的本质,是最快速透析问题根源的一把利器。
思考模式是先从Why出发,为什么要这么做,这么做的理念是什么,从内心激发出感性的情感,产生驱动力;
近而再思考How,设定目标一步步解决;最后做出来的结果就是What,更加贴合最初的理念。
- Why
:思考为什么要这么做,我们的目标、理念;
- How
:采用什么方法、措施;
- What
:结果的表现形式。
对一家企业、一个人思考why的过程则是对原则、边界、价值观的一个确定,提供了一个解决问题的通用模型。
03 10+10+10旁观思维模型
面对一个决策或选择,当你犹豫不决时,可以想一下:
10分钟后,自己是怎么看待自己现在的决策,依然保持一致亦或会后悔;
10个月后,你又会如何思考自己10个月以前的这个决策;
10年后,自己如何看待自己这个10年前的判断与决策。
这个思维模型,可以应用在:临时的判断,大的决策,预测自己的未来等。
04 反熵增思维模型
从一个系统、一个组织,再到一个星球,甚至我们每个人,都符合熵增定律。
我们会变得混乱、无序、僵化、没有活力,直至在这种混乱中走向消亡。
值得庆幸的是,宇宙是平衡的,在熵增的大前提下,给了我们一条不同的路,反熵增,也即自组织、生命化。
亚马逊的CEO贝佐斯对于反熵增的理解非常深刻。他把亚马逊的服务做得足够开放,所以才有了亚马逊云。
对于新生事物,哪怕是取得一点点的成绩,他都会大加赞赏,要求主管以上级别员工每周都要读一遍《创新者的窘境》。
反熵增就是重现生命。行星从星云中诞生,行星上产生了岩石圈、大气、河流、季风、泉水、矿藏,这些都是组织化的过程,是对无序的反抗。
这种有序化、组织化进程的顶峰,便是生命的产生:DNA团块、单细胞生物、多细胞生物、植物和动物,一直到最精巧的组织化结构——人类。
人老后,最好的状态就是复归婴儿和自然。
一个企业,要让自己反熵增,就是让自己更有活力,更开放,更多地适应外部变化,让其在环境中自我进化。
同时,可以不断生出独立的新的业务,新的业务也可以不断进化。
从本质上来讲,延续的发展就是一个熵增的过程,而要想突破非连续性,必须要“生”出新的曲线,这才是对抗熵增最好的办法。
05 三层解释思维模型
对于一个事物,可以有三层解释:
现实层、技术层、底层
。
现实层会解释浅显的,大多数人能看到的因果;
技术层会解释现实背后的规律,是现象之下,是一种背景带来的规律,是一种看得见技能的规律;
而底层,则是一种可以广泛适用的规律,是深层次思维模型,通达人性,洞悉法则。
三层解释思维模型,可以应用于深度剖析一个事件的原因,了解一个复杂事物的规律。
06 反脆弱思维模型
事物可分为三类:
脆弱、强悍、反脆弱
。
脆弱的事物,在受到外界压力时会破碎、受损,就像玻璃杯掉到地上会碎;强悍的事物,在遭遇外界压力时,不会受其影响。
而反脆弱的事物,可以在这个波动的世界中,伴随压力而进化,让自己变得更强大。
不要被压力打垮,它是你进化最好的能量。外界的环境变化会筛选出真正的反脆弱者。反脆弱思维模型可以应用于:
- 从困境中理性分析,提升认知,获得能量;
- 从压力中回归内心,提升胸怀和气度;
- 从局限中重新定位,提升眼光和格局。
而自然,也具备反脆弱性。在这个世界上,自然的事物很多都有弹性,具有反脆弱性。
自然的特点有很多,在自然中有春夏秋冬这样普遍的规律,适应性强的生物从这样的波动中进化,而体型大笨拙的生物如恐龙因此而灭绝;
人的身体也符合自然的规律,也具有反脆弱性,人骨折了,生出来的骨头会更加强壮,中过毒的人也会具有抗毒的特性。
反脆弱本身是可以面对风险,可以从风险中受益成长。
面对未来的不确定性,我们可以这样做:
- 利用不对称性,小投入,高产出。
- 成为多元化,让自己不只一种技能或身份。
- 相信未来的非线性,会给我们更多的机会与乐趣。这个世界,正因为有了非线性才会有新的生物不断出现,新的事物代替旧的事物,我们才会不断成长不断精进。
07 复利原理
爱因斯坦说:复利是世界的第八大奇迹。
巴菲特说:人生就像滚雪球,关键是要找到足够湿的雪和足够长的坡。
查理·芒格说:同时理解复利的力量和获得它的困难,是理解许多事情的核心和灵魂。
在有限的时间,把有限的精力和财富,持续而反复地投入到某一领域,长期坚持下去,最终产生的积极影响,会如雪球越滚越大,它带来的回报一定超过你的想象。
这就是经济学中典型的复利思维。
大多数人终其一生都不会去运用复利,也体会不到复利的威力。
复利思维需要我们用发展和长远的眼光去看待事物。
08 完型融合思维模型
完成一件事情,除了要有完整、清晰的逻辑思路,还需要多种元素进行融合, 比如:人的资源、物钱的资源、时机大环境等。
这就像完成一个陶瓷作品的创作:
- 除了有创造的图纸、陶瓷还需要泥,相当于是物钱相关的资源;
- 而水就像是人,需要把泥组合起来;陶瓷的烧制,还需要合适的温度,速度,这就像看不见的时机与背景环境;
- 而陶瓷上的雕琢,就像是对事情细节的处理。先做什么后做什么的顺序,也至关重要。
所以,一个项目要取得成功,除了要有可能实现的规划,还需要有充足的人力准备、事情分解分层、方法论支持、流程制度激励支持、 稳定明确的责权分解说明,还要有应急方案与思路。
这样做起事来,才可行云流水,事半功倍。
完型融合思维模型可以应用在:事情的执行、思考事物产生原因、预测人的判断等。
只有考虑足够多的因素,以及整体需要的相互支持,因素之间的相互关系,才能更准确地判断与分析。
09 笛卡尔思维模型
笛卡尔是一个伟大的哲学家,他提出一个大胆的观点,你怎么能证明这个世界是真实的?这个世界有什么是不能被怀疑的?
他思考再思考,一直没有抓到那个基石。直到某一瞬间,就像闪电击中了他。
他意识到,只有一件事不能再被怀疑了,那就是:我在怀疑这件事。
也就是:
I think,therefore I am
。
这件事情是确定的,所以我是存在的,所以不管当下世界是不是真,一定存在一个世界。
而当下世界,我不知道它是不是真的存在。
这就是批判性思维,大胆质疑一切。我们以为科学的演化是继承,其实是颠覆。
下一代科学家几乎都颠覆上一代。
就如乔布斯说:
stay hungry,stay foolish
;股神会说:
我唯一知道的事情,就是我什么都不知道
。
在人的认知经验里,过往的成功范式越多,给自己的束缚也越大。
10 获得性偏差思维模型
人们对一个事物判断失误,往往不是因为他什么都不知道;而是因为把注意力太多都放在了已知部分。
从一个大的完型角度,你了解的信息,可能不足5%,所以,自己已经获得的信息也许不仅不重要,很有可能还是局限的,有偏见的。
获得性偏差会出现在哪些生活中的场景呢?比如:
- 人们在找新工作时,对自己曾经做过的部分,往往难以放下。
- 对固有观念的坚持,甚至是固执。
- 对没用旧物的留恋。
我们很多人都遇到过类似情况,很多东西明知没用却舍不得扔。
殊不知,房间在熵增,你的生活环境因为不够简洁,你也会变得混乱、迟钝、得不偿失。
此外,新事物也很难进来,你的生活逐渐陷入了低效与僵化。
如何克服获得性偏差呢?
- 放低自己,谦虚心态,虚怀若谷;
- 独立思考,从本质入手,更多用演绎法而不是归纳法,用事物的本质去推理,而不是持续的用之前的经验;
- 分类整理。把信息归类整理,把一切变得秩序化;
- 重新分析,评估环境和信息,哪些是合理的,哪些是落后的,哪些是可以升级的;
- 懂得舍弃和放下;
- 动态心态,拥有只是暂时,变化是永恒的。
11 排列组合思维模型
和复利模型一样,排列组合模型不仅是一种数学工具,也是一种可以提升我们决策质量的思维方式。
很多时候,影响决策的因素很多,通过分类、分步,就可以形成不同的排列组合方式。
万事万物都是由其构成的元素排列组合成的,思维是知识的运动,是知识的排列组合、取舍。
前所未有的知识排列组合就是创新,合乎客观的有价值的思维创新的外化和物化,就是理论创新、创造发明。
查理·芒格的多元思维模型,本质就是一种多维组合思想,把不同的跨学科的知识汇集在一起,解决一个问题。
不同问题和学科所占权重不一样,综合起来考虑问题就更全面,正确概率就更高。
一个大问题,可以分解成很多相关元素,这样方便我们看清楚整个问题,然后找到关键点,从关键点入手可以起到事半功倍的效果。
很多元素组合在一起,可以对一个问题看得更全面,避免陷入查理·芒格口中的“铁锤人”思维。
12 费马帕斯卡系统
在知识、能力、努力、耐心这些所有的品质中,查理·芒格最看重的是理性。
查理·芒格说:“你必须看到这个世界真实的样子,而不是你以为的样子、或者你希望的样子,只有这样你才能做出正确的选择。” 费马帕斯卡系统就是认识真实世界的基本工具。
费马帕斯卡系统是概率论的基本原则。
在生活中,充满了各种诱惑,人们根据经验和各种心理倾向做决定,从而掉入了很多的陷阱。
通过费马帕斯卡系统的学习理解,我们要从认知上明白,事情的实际概率是多少,在有了清晰的认识之后,再做决定将更加理性。
把这些基本的基础数学概率方法,变成我们生活中的一部分,才不会将自己的优势拱手送给别人。
13 前景理论
前景理论,是风险决策的一个重要思维模型,由诺贝尔经济学奖心理学家丹尼尔·卡尼曼提出,描述和预测人们在面临风险决策过程中的行为理论。
前景理论分析框架有三个特征:
- 一是大多数人在面临获得时,是风险规避的;
- 二是大多数人在面临损失时,是风险偏爱的;
- 三是人们对损失比获得更敏感。
具体看:
- 确定效应:“二鸟在林,不如一鸟在手”,在确定的收益和“赌一把”之间,多数人会选择确定的好处,落袋为安心理。
- 反射效应:在确定的损失和“赌一把”之间,做一个抉择,多数人会选择“赌一把”。
- 损失规避:白捡的100元所带来的快乐,难以抵消丢失100元所带来的痛苦。
14 心流模型
“心流”是指我们在做某些事情时,那种全神贯注、投入忘我的状态——这种状态下,你甚至感觉不到时间的存在。在事情完成后,我们会有一种充满能量且非常满足的感受。
这是关于人幸福快乐的理论,让人沉浸在心流中的条件需要:
- 明确的目标,合适难度的任务——既不会焦虑,也不会无趣。
- 及时的反馈——对进步的满足感。
为何游戏如此受欢迎,就是游戏的设计满足心流理论,如果游戏的定义扩大,把学习、工作、运动、教育包含进来,去评估自己在做的事是否满足心流三点,这样自然会过得幸福快乐。
- 发挥自己的某种能力。
- 精神完全集中,对手上的事情有控制力 。
心流状态,是我们能够在工作中达到的最美好、最平和的状态。通过一种心流状态又会产生新的心流状态。
成功的人,能够成功地将他们的一生,变成一种单纯的心流状态。他们在生命中各个部分紧紧地连接到了一起,所有活动都有了意义。
15 奥卡姆剃刀定律
“奥卡姆剃刀定律”
,又称
“简约法则”
, 这个原理最早至少能追溯到亚里士多德的“自然界选择最短的道路”。
核心内容为
“如无必要,勿增实体”
,即简单有效原理。
依据最小能量原则,我们的生活应尽可能简单,而简单的有效途径就是养成好的习惯。
自动挡汽车在逐步替代手动挡汽车,也是因为自动挡对大多数用户来说满足“简单有效原理”。
面对复杂的投资市场,应拿起奥卡姆剃刀,把复杂事情简单化,简化自己的投资策略,对那些消耗了大量金钱、时间、精力的事情加以区分,然后釆取步骤去摆脱它们。
最后我们以弗里德里克·迈特兰德的名言作结:
“简单是长期努力工作的结果,而不是起点。”
相关文章:

15个顶级思维模型
今天给大家分享几个思维模型,无论是数分、数开还是其他岗位,都会有所启发。 查理芒格认为,每个学科都是从一个独特的角度去切入了解这个世界,都是一个摸象的瞎子。 要超越普通人的认知决策,就必须掌握多个核心思维模…...
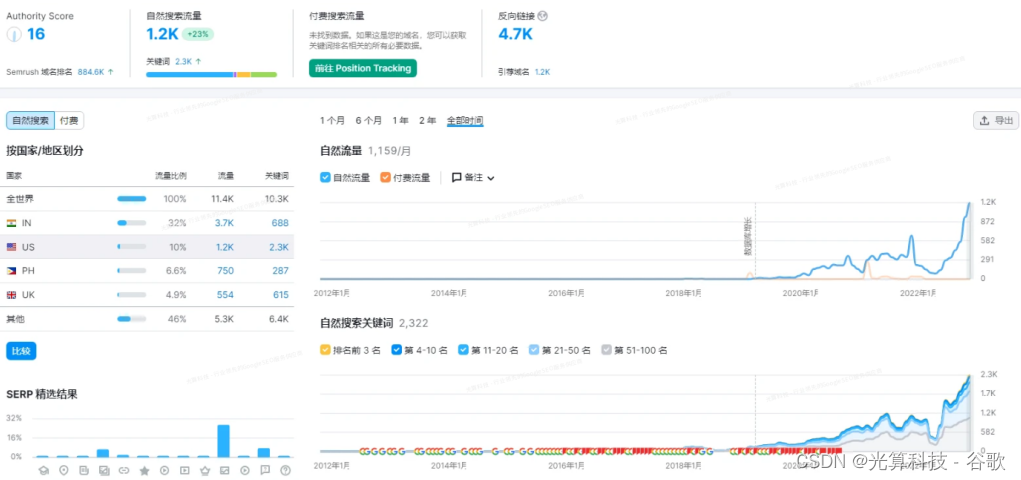
外贸谷歌优化,外贸google SEO优化费用是多少?
本文主要分享关于做外贸网站的谷歌seo成本到底需要投入多少这一件事。 本文由光算创作,有可能会被剽窃和修改,我们佛系对待这种行为吧。 那么外贸google SEO优化费用是多少? 答案是:2w~25w。 好,看到这个答案先别激…...
 | 机试题算法思路)
华为OD机试 - 统计匹配的二元组个数(Python) | 机试题算法思路
最近更新的博客 华为OD机试 - 招聘(Python) | 备考思路,刷题要点,答疑 【新解法】华为OD机试 - 五键键盘 | 备考思路,刷题要点,答疑 【新解法】华为OD机试 - 热点网络统计 | 备考思路,刷题要点,答疑 【新解法】华为OD机试 - 路灯照明 | 备考思路,刷题要点,答疑 【新解…...
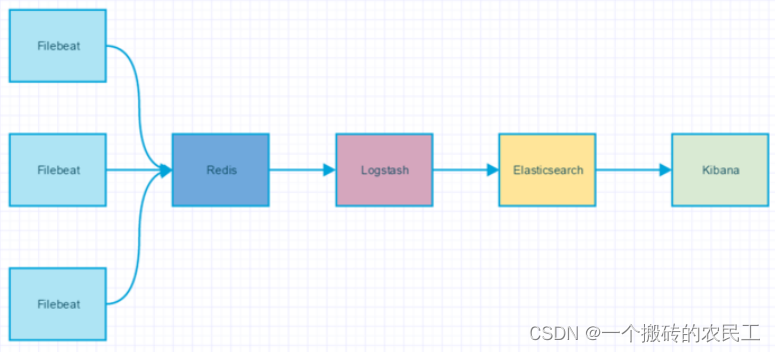
Java 日志简介
目录1、Slf4j2、Log4j3、LogBack4、Logback 优点5、ELK1、Slf4j slf4j 的全称是 Simple Loging Facade For Java,即它仅仅是一个为 Java 程序提供日志输出的统一接口,并不是一个具体的日志实现方案,就比如 JDBC 一样,只是一种规则…...

HTTPS协议原理---详解六个加密方案
目录 一、HTTPS 1.加密与解密 2.我们为什么要加密? 3.常见加密方式 ①对称加密 ②非对称加密 4.数据摘要 5.数字签名 二、HTTPS的加密方案 1.只是用对称加密 2.只使用非对称加密 3.双方都使用非对称加密 4.非对称加密+对称加密 中间人攻…...
纯css实现坤坤经典动作-“铁山靠”
背景 2023年2月16日,晴,今天没有工作,一直在掘金摸鱼,摸的我好累。 不行!我得找点有意义的事情做! 此时间,我发的一条沸点竟然有小黑子给我评论,\ 我看到之后气不打一处来ÿ…...
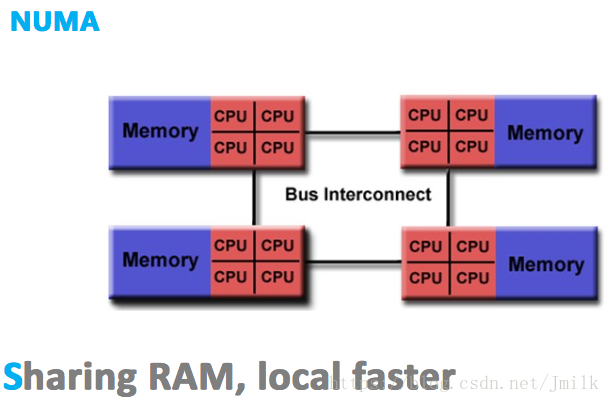
Linux 操作系统原理 — NUMA 体系结构
目录 文章目录 目录NUMA 体系结构NUMA 的基本概念查看 Host 的 NUMA TopologyBash 脚本DPDK 脚步NUMA 体系结构 NUMA(Non-Uniform Memory Access,非一致性存储器访问)的设计理念是将 CPU 和 Main Memory 进行分区自治(Local NUMA node),又可以跨区合作(Remote NUMA nod…...
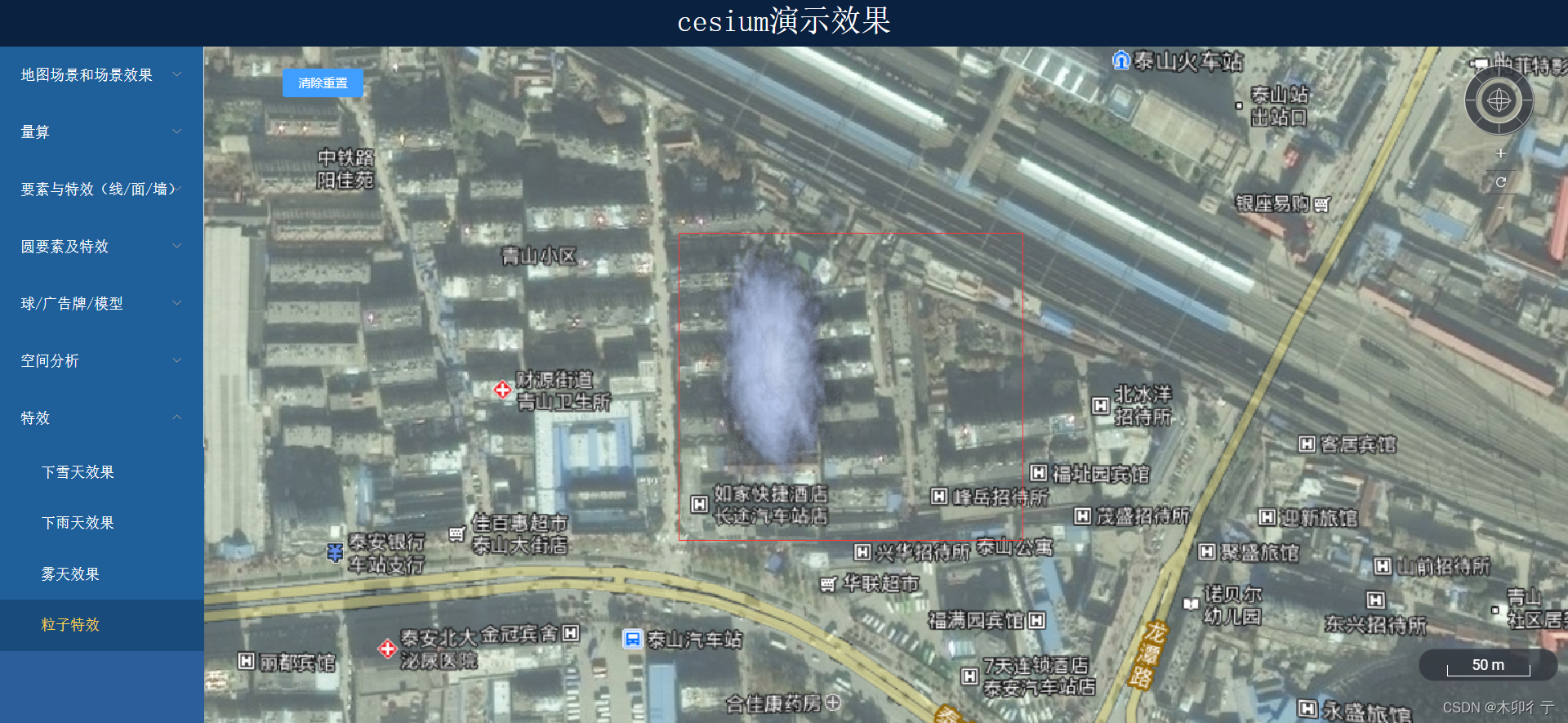
cesium学习记录01
1,将右弦GISer的cesium实战系列的大部分功能(25-110) 都又跟着走了一遍(大部分是CTRL CCTRL V) 2,代码SVN地址(用户名:liu 密码:123) (如果我没有遗漏上传…...

Linux延时队列工作原理与实现
当进程要获取某些资源(例如从网卡读取数据)的时候,但资源并没有准备好(例如网卡还没接收到数据),这时候内核必须切换到其他进程运行,直到资源准备好再唤醒进程。 waitqueue (等待队列) 就是内核…...

【Python】scipy稀疏矩阵的奇异值分解svds
文章目录基本原理scipy实现测试基本原理 当AAA是方阵时,可以很容易地进行特征分解:AWΣW−1AW\Sigma W^{-1}AWΣW−1,其中Σ\SigmaΣ是AAA的特征值组成的对角矩阵。如果WWW由标准正交基组成,则W−1WTW^{-1}W^TW−1WT,…...

网络安全等级保护基础知识汇总
等保 全称是网络安全等级保护,分为两个阶段 等保1.0 1994年国务院147令《中华人民共和国计算机信息系统安全保护条例》 等保2.0 2017年 网络安全法,21条规定的 国家实行网络安全等级保护制度,等保进入了有法可依阶段。 2019年国标22239-2019版…...

ros1使用过程中遇到的问题记录
Failed to fetch current robot state如果使用的是moveit助手生成的demo.launch文件启动机械臂的话,应该是其他在运行的自己写的节点代码中少了spin函数,因为getCurrentPose函数依赖于spin,也可以使用AsyncSpinner。具体看下面这个链接https:…...
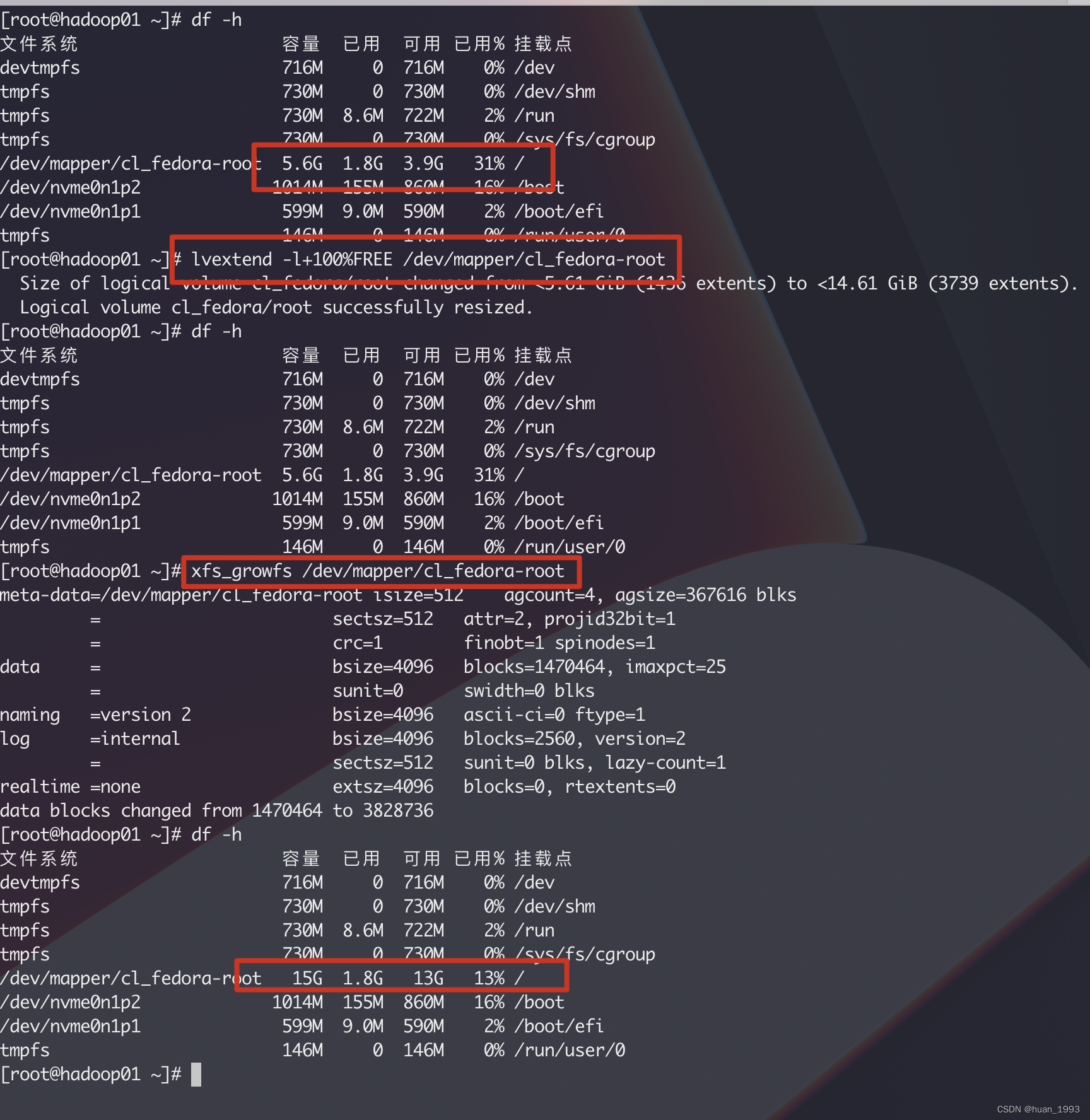
centos7给已有分区进行扩容
1、背景 最近我在虚拟机上安装软件,发现磁盘空间不足,通过上网查找资料,发现可以通过如下方法进行磁盘扩容,此处进行记录一下。 2、实现扩容 1、虚拟机上添加一个新的硬盘 2、查看我们刚刚加入的硬盘 此处我们可以看到/dev/nvm…...

package.json
{"name": "project-name", 项目名字"version": "0.1.0", 版本号"private": true, 项目包,不需要发版"scripts": { 脚本"serve": "vue-cli-service serve", 运行命令后缀是 se…...
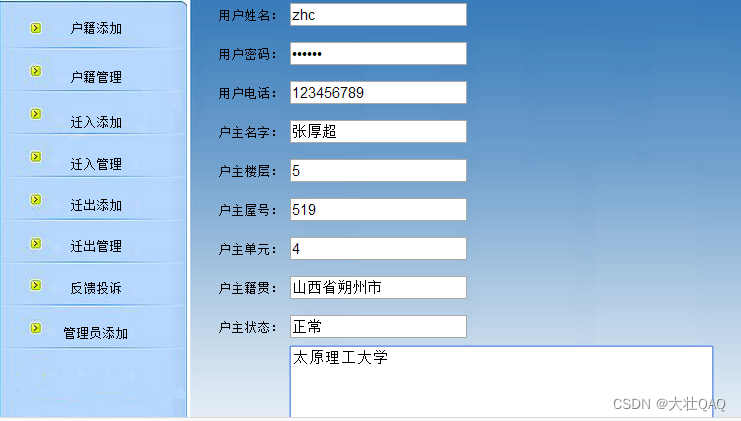
【项目精选】户籍管理系统(视频+论文+源码)
点击下载源码 当今社会人们生活质量越来越高,人们对生活品质的追求不断提升,对于孩子求学,变更住所等情况时有发生,因此对于户籍变动管理就显得十分重要,管理用户的户籍信息可以有效防止信息错乱,信息管理过…...

【IP技术】网络安全防护措施
网络安全威胁造成的形式主要包含运用系统软件缺点或侧门,运用网络防火墙安全隐患,内部结构客户的泄密、泄露和毁坏,动态口令进攻和拒绝服务式攻击等。针对该网络安全威胁,现阶段的预防措施主要有五种:1.访问控制技术&a…...
)
基于AIOT技术的智慧教室智能物联管控系统设计与实现(提纲)
摘要随着物联网技术的不断发展和智能化的不断推进,智慧教室已经成为现代教育中不可或缺的一部分。本文提出了一种基于AIOT技术的智慧教室智能物联管控系统设计与实现方案,该方案集成了物联网技术、人工智能技术、大数据技术和云计算技术等先进技术&#…...

C 指针的深造
C 指针1 关于内存那点事2 指针的概念3 指针变量的定义方法4 指针的分类5 指针和变量的关系6 指针和数组元素之间的关系7 指针数组8 指针的指针9 字符串和指针9.1 字符串的定义9.2 字符串的可修改性:9.3 初始化赋值9.4 使用时赋值9.5 字符串和指针总结10 数组指针11 …...
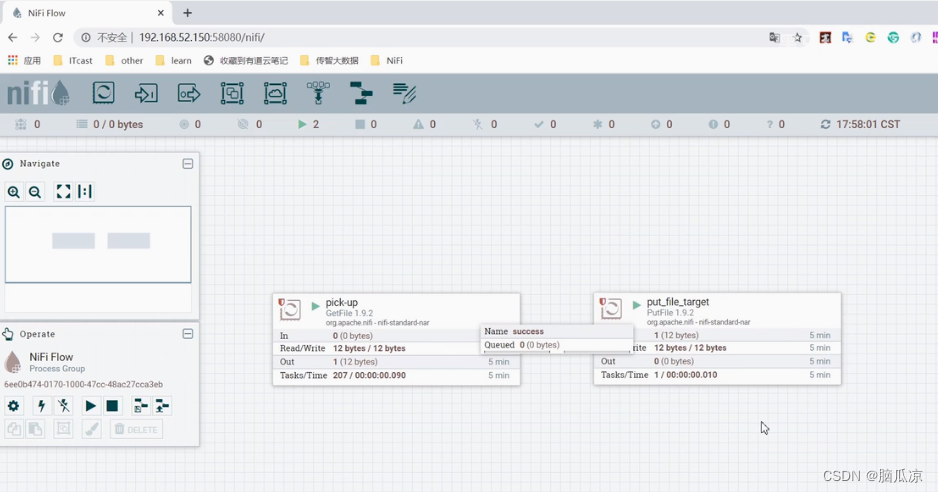
大数据之-Nifi-应用场景2-2_设置putfile处理器自动创建目标文件夹_以及存在重复文件时自动覆盖---大数据之Nifi工作笔记0006
上一节我们留了两个问题,一个是,如果我们没有创建putfile要写入的目标文件夹,会报错吗? 可以看到我们putfile目标文件夹是上面这个目录 我们来试一试,如果目标文件夹不存在,putfile处理器会自动创建吗 首先我们删除这个target目标文件夹 然后我们进入cd source目录,源文件夹目…...

buuctf Web 下
9.[ACTF2020 新生赛]Exec 访问url: http://cc3c6c27-e2df-4665-baba-1d9a32dc963e.node3.buuoj.cn/ 首页如下: 直接ping ip可以得到结果 常见管道符 1、|(就是按位或),直接执行|后面的语句 127.0.0.1 | cat /flag…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...
