【css】组合器
组合器是解释选择器之间关系的某种机制。在简单选择器器之间,可以包含一个组合器,从而实现简单选择器难以达到的效果。
CSS 中有四种组合器:
-
后代选择器 (空格):匹配属于指定元素后代的所有元素,示例:div p 选择div元素后代中的p,包括它的子孙十八代
-
子选择器 (>) :指定元素子元素的所有元素。div > p,选择div元素下的子元素,只包括子元素
-
相邻兄弟选择器 (+) :相邻兄弟选择器匹配所有作为指定元素的相邻同级的元素。兄弟(同级)元素必须具有相同的父元素,“相邻”的意思是“紧随其后”
-
通用兄弟选择器 (~):通用兄弟选择器匹配属于指定元素的同级元素的所有元素
1、后代选择器 (空格)
匹配属于指定元素后代的所有元素,示例:div p 选择div元素后代中的p,包括它的子孙十八代
代码:
<style>
div p {background-color: yellow;
}
</style>
</head>
<body><div><p>div 段落 1。</p><p>div 段落 2。</p><div> div2 <p> div2 中的 p</p></div><section><p>div 段落 3。</p></section>
</div><p>段落 4。不在 div 中。</p>
<p>段落 5。不在 div 中。</p></body>
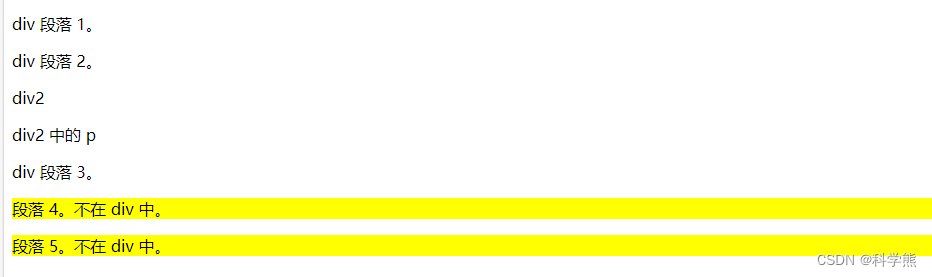
后代选择器选择的元素的所有符合的后代元素,包括子孙十八代,上面的代码中"div 段落 3"的 p也被选择中,这一点和后面的子选择器最大的区别。
渲染效果:

**2、子选择器 (>) **
指定元素子元素的所有元素。div > p,选择div元素下的子元素,只包括子元素
代码:
<style>
div > p {background-color: yellow;
}
</style>
</head>
<body>
<div><p>div 段落 1。</p><p>div 段落 2。</p><div> div2 <p> div2 中的 p</p></div><section><p>div 段落 3。</p></section>
</div><p>段落 4。不在 div 中。</p>
<p>段落 5。不在 div 中。</p></body>
“div 段落 3”属于孙子p,在子选择器中不被选中。
渲染效果:

3、相邻兄弟选择器 (+)
相邻兄弟选择器匹配所有作为指定元素的相邻同级的元素。兄弟(同级)元素必须具有相同的父元素,“相邻”的意思是“紧随其后”
代码:
<style>
div + p {background-color: yellow;
}
</style>
</head>
<body>
<div><p>div 段落 1。</p><p>div 段落 2。</p><div> div2 <p> div2 中的 p</p></div><section><p>div 段落 3。</p></section>
</div><p>段落 4。不在 div 中。</p>
<p>段落 5。不在 div 中。</p></body>
渲染效果:相邻兄弟选择器强调的事“紧随其后”的,div元素同级一级并且紧随其后的是“<p>段落 4。不在 div 中。</p>”。

4、通用兄弟选择器 (~)
通用兄弟选择器匹配属于指定元素的同级元素的所有元素
代码:
<style>
div ~ p {background-color: yellow;
}
</style>
</head>
<body><div><p>div 段落 1。</p><p>div 段落 2。</p><div> div2 <p> div2 中的 p</p></div><section><p>div 段落 3。</p></section>
</div><p>段落 4。不在 div 中。</p>
<p>段落 5。不在 div 中。</p></body>
渲染效果:与div同级并且是p的就包括“<p>段落 4。不在 div 中。</p>”和“<p>段落 5。不在 div 中。</p>”
相关文章:

【css】组合器
组合器是解释选择器之间关系的某种机制。在简单选择器器之间,可以包含一个组合器,从而实现简单选择器难以达到的效果。 CSS 中有四种组合器: 后代选择器 (空格):匹配属于指定元素后代的所有元素,示例:div …...

HTTPS、TLS加密传输
HTTPS、TLS加密传输 HTTPS、TLS加密传输1、HTTPS(HyperText Transfer Protocol Secure)2、TLS HTTPS、TLS加密传输 1、HTTPS(HyperText Transfer Protocol Secure) HTTPS(HyperText Transfer Protocol Secure&#x…...

docker frp 搭建 http + stcp 代理
所需服务器 2台 一台具有国外公网ip 一台具有国内 ip 内网外网都可以 外公网ip服务器配置如下 cat docker-compose.yamlversion: "2" services:frps:image: alpine:latesthostname: frpsrestart: alwayscontainer_name: frpsprivileged: trueuser: rootcommand: […...
项目出bug,找不到bug,如何拉回之前的版本
1.用gitee如何拉取代码 本文为转载于「闪耀太阳a」的原创文章原文链接:https://blog.csdn.net/Gufang617/article/details/119929145 怎么从gitee上拉取代码 1.首先找到gitee上想要拉取得代码URL地址 点击复制这里的https地址 1 ps:(另外一种方法&…...
vue-cli
vue-cli脚手架 案例一: 案例二: 案例三: 一、脚手架简介 Vue脚手架是Vue官方提供的标准化开发工具(开发平台),它提供命令行和UI界面,方便创建vue工程、配置第三方依赖、编译vue工程 1. …...
的不正确)
android获取屏幕分辨率的正确方法;获取到分辨率(垂直方向像素)的不正确
我通过下面的方法去获取屏幕分辨率的,但获取到的分辨率有时会不准确。原因是此方法有时候会忽略一些布局或控件的高度,从而得不到正确的高度。 public static String getDeviceResolution(Context context){//从系统服务中获取窗口管理器WindowManager w…...

机器学习笔记之优化算法(八)简单认识Wolfe Condition的收敛性证明
机器学习笔记之优化算法——简单认识Wolfe Condition收敛性证明 引言回顾: Wolfe \text{Wolfe} Wolfe准则准备工作推导条件介绍推导结论介绍 关于 Wolfe \text{Wolfe} Wolfe准则收敛性证明的推导过程 引言 上一节介绍了非精确搜索方法—— Wolfe \text{Wolfe} Wolf…...

通过win+r安装jupyter报错
通过pip install jupyter安装jupyter报错处理办法 1、python 更新到最新版,最好多执行几次后在安装jupyter python.exe -m pip install --upgrade pip 2、通过镜像安装 pip install jupyter --force-reinstall pip -i http://pypi.douban.com/simple/ --trusted-h…...

C#声明一个带返回值的委托
1、声明 public delegate string TestDel(string str); 2、使用 TestDel t; t (string str) > str; t (string str) > str "1"; t (string str) > str "2"; t (string str) > str "3"; Console.WriteLine(t ("hhhh&qu…...

Flutter 自定义view
带进度动画的圆环。没gif,效果大家自行脑补。 继承CustomPainter,paint()方法中拿到canvas,绘制API和android差不多。 import package:flutter/material.dart;class ProgressRingPainter extends CustomPainter {double strokeWidth 20;Col…...

Ubuntu新装系统报错:sudo: vim:找不到命令
问题: 新安装的老版本Ubuntu系统,发现在使用vim命令的时候报错: sudo:vim:找不到命令 解决办法 这是因为没有安装vim,直接运行下面命令安装vim sudo apt-get install vim...

Vue3自定义简单的Swiper滑动组件-触控板滑动鼠标滑动左右箭头滑动-demo
代码实现了一个基本的滑动功能,通过鼠标按下、鼠标松开和鼠标移动事件来监听滑动操作。 具体实现逻辑如下: 在 onMounted 钩子函数中,我们为滚动容器添加了三个事件监听器:mousedown 事件:当鼠标按下时,设置…...
三个主流数据库(Oracle、MySQL和SQL Server)的“单表造数
oracle 1.创建表 CREATE TABLE "YZH2_ORACLE" ("VARCHAR2_COLUMN" VARCHAR2(20) NOT NULL ENABLE,"NUMBER_COLUMN" NUMBER,"DATE_COLUMN" DATE,"CLOB_COLUMN" CLOB,"BLOB_COLUMN" BLOB,"BINARY_DOUBLE_COLU…...

TypeScript 中【class类】与 【 接口 Interfaces】的联合搭配使用解读
导读: 前面章节,我们讲到过 接口(Interface)可以用于对「对象的形状(Shape)」进行描述。 本章节主要介绍接口的另一个用途,对类的一部分行为进行抽象。 类配合实现接口 实现(impleme…...
JavaWeb 手写Tomcat底层机制
目录 一、Tomcat底层整体架构 1.简介 : 2.分析图 : 3.基于Socket开发服务端的流程 : 4.打通服务器端和客户端的数据通道 : 二、多线程模型的实现 1.思路分析 : 2.处理HTTP请求 : 3.自定义Tomcat : 三、自定义Servlet规范 1. HTTP请求和响应 : 1 CyanServletRequest …...
Gof23设计模式之组合模式
1.定义 组合模式又名部分整体模式,是用于把一组相似的对象当作一个单一的对象。组合模式依据树形结构来组合对象,用来表示部分以及整体层次。这种类型的设计模式属于结构型模式,它创建了对象组的树形结构。 2.结构 组合模式主要包含三种…...
龙芯积极研发二进制翻译,提升软硬件兼容性,提高LoongArch架构
根据8月8日Phoronix报道,龙芯正在积极研发龙芯二进制翻译功能(Loongson Binary Translationm,LBT)以提高LoongArch架构与其他处理器(如MIPS/x86/Arm)的二进制翻译能力,这重要举措将显著提升龙芯…...
3天爆肝整理,自动化测试-YAML文件读写实战(超细总结)
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 YAML 简介 YAML&…...

算法通关村——透彻理解二分查找
1. 循环法 public static int binarySearch(int[] arr, int low, int high, int target) {while (low < high) {// 这样写主要是避免溢出的情况,以及>>优先级小于,避免出现死循环int mid low ((high - low) >> 1);if (arr[mid] target…...
刷题指南 —— 第六弹(⭐有点难度⭐))
PAT(Advanced Level)刷题指南 —— 第六弹(⭐有点难度⭐)
一、1010 Radix 1. 问题重述 2. Sample Input1 6 110 1 103. Sample Output1 24. Sample Input 2 1 ab 1 25. Sample Output 2...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...
