代码随想录—力扣算法题:209长度最小的子数组.Java版(示例代码与导图详解)
版本说明
当前版本号[20230808]。
| 版本 | 修改说明 |
|---|---|
| 20230808 | 初版 |
目录
文章目录
- 版本说明
- 目录
- 209.长度最小的子数组
- 思路
- 暴力解法
- 滑动窗口
- 两种方法的区别
- 总结
209.长度最小的子数组
力扣题目链接
更多内容可点击此处跳转到代码随想录,看原版文件
给定一个含有 n 个正整数的数组和一个正整数 s ,找出该数组中满足其和 ≥ s 的长度最小的 连续 子数组,并返回其长度。如果不存在符合条件的子数组,返回 0。
示例:
- 输入:s = 7, nums = [2,3,1,2,4,3]
- 输出:2
- 解释:子数组 [4,3] 是该条件下的长度最小的子数组。
提示:
- 1 <= target <= 10^9
- 1 <= nums.length <= 10^5
- 1 <= nums[i] <= 10^5
思路
暴力解法
这道题目暴力解法当然是 两个for循环,然后不断的寻找符合条件的子序列,时间复杂度很明显是O(n^2)。
代码如下:
class Solution {/*** 使用滑动窗口方法来找到最小长度的子数组*s 目标值* nums正整数数组* 最小长度的子数组的长度*/public int minSubArrayLen(int s, int[] nums) {int result = Integer.MAX_VALUE; // 最终的结果,默认为最大值int sum = 0; // 子序列的数值之和int subLength = 0; // 子序列的长度for (int i = 0; i < nums.length; i++) { // 设置子序列起点为isum = 0;for (int j = i; j < nums.length; j++) { // 设置子序列终止位置为jsum += nums[j];if (sum >= s) { // 一旦发现子序列和超过了s,更新resultsubLength = j - i + 1; // 取子序列的长度result = Math.min(result, subLength); // 更新result为较小值break; // 因为我们是找符合条件最短的子序列,所以一旦符合条件就break}}}// 如果result没有被赋值的话,就返回0,说明没有符合条件的子序列return result == Integer.MAX_VALUE ? 0 : result;}
}
- 时间复杂度:O(n^2)
- 空间复杂度:O(1)
后面力扣更新了数据,暴力解法已经超时了。
滑动窗口
接下来就开始介绍数组操作中另一个重要的方法:滑动窗口。
所谓滑动窗口,就是不断的调节子序列的起始位置和终止位置,从而得出我们要想的结果。
在暴力解法中,是一个for循环滑动窗口的起始位置,一个for循环为滑动窗口的终止位置,用两个for循环 完成了一个不断搜索区间的过程。
那么滑动窗口如何用一个for循环来完成这个操作呢?
首先要思考 如果用一个for循环,那么应该表示 滑动窗口的起始位置,还是终止位置。
如果只用一个for循环来表示 滑动窗口的起始位置,那么如何遍历剩下的终止位置?
此时难免再次陷入 暴力解法的怪圈。
所以 只用一个for循环,那么这个循环的索引,一定是表示 滑动窗口的终止位置。
那么问题来了, 滑动窗口的起始位置如何移动呢?
这里还是以题目中的示例来举例,s=7, 数组是 2,3,1,2,4,3,来看一下查找的过程:
第一步:设i,j为滑动窗口开始、终止位置

第二步:i开始向右走,直到走到累加的和大于等于7停下来
2 + 3 = 5 < 7
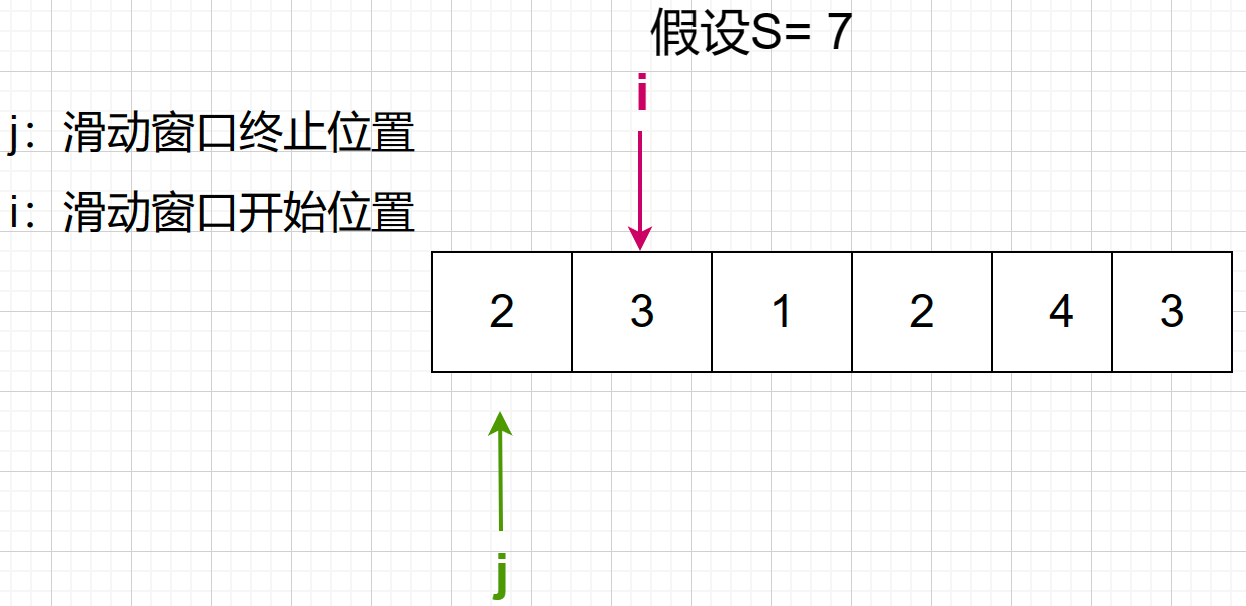
2 + 3 + 1 = 6 < 7
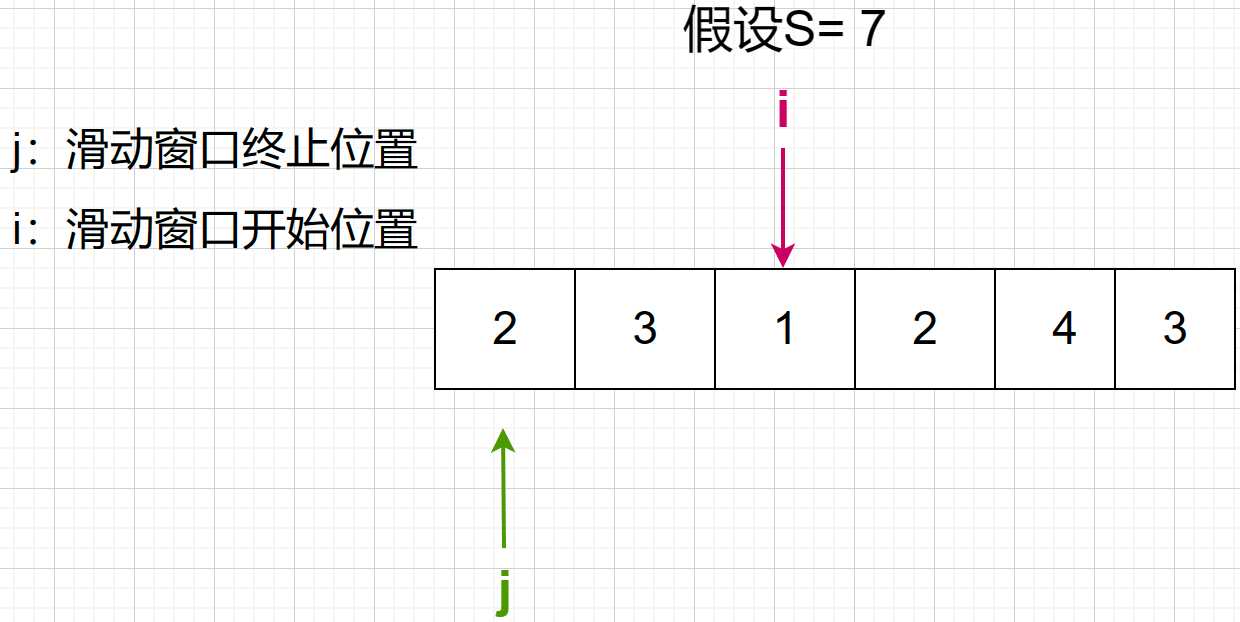
2 + 3 + 1 + 2 = 8 > 7 ,长度为4
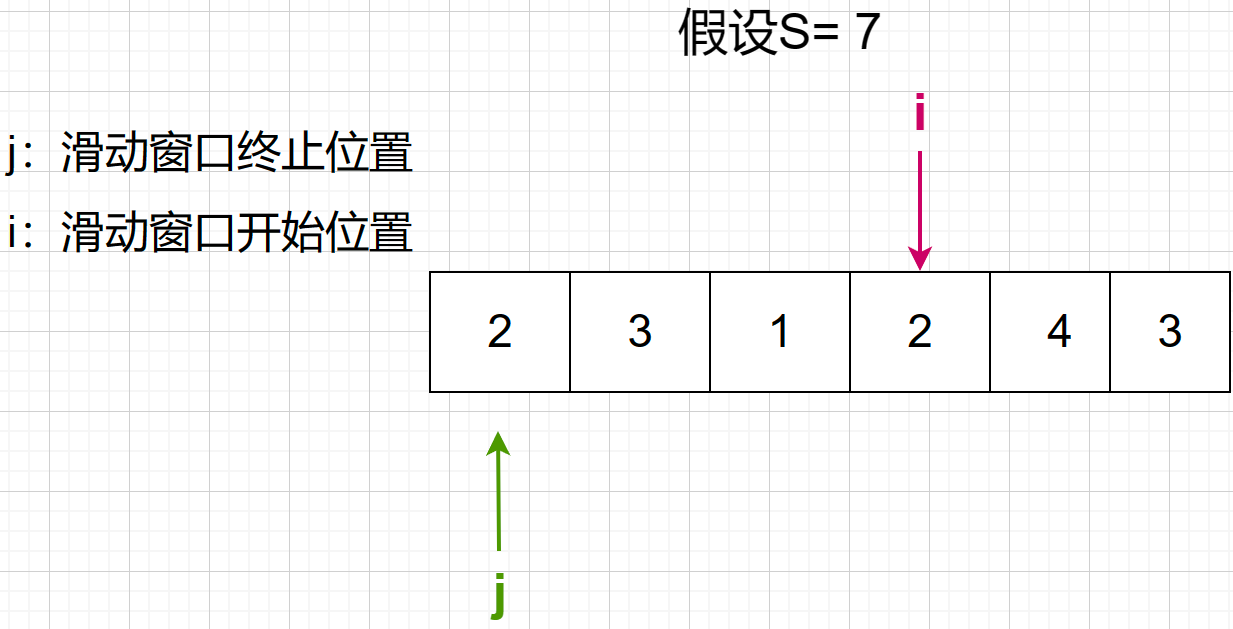
第三步,当出现i累加的和大于等于7并且已经停下来后,终止位置j开始向右移动,当走到滑动窗口不再大于等于7就停下来
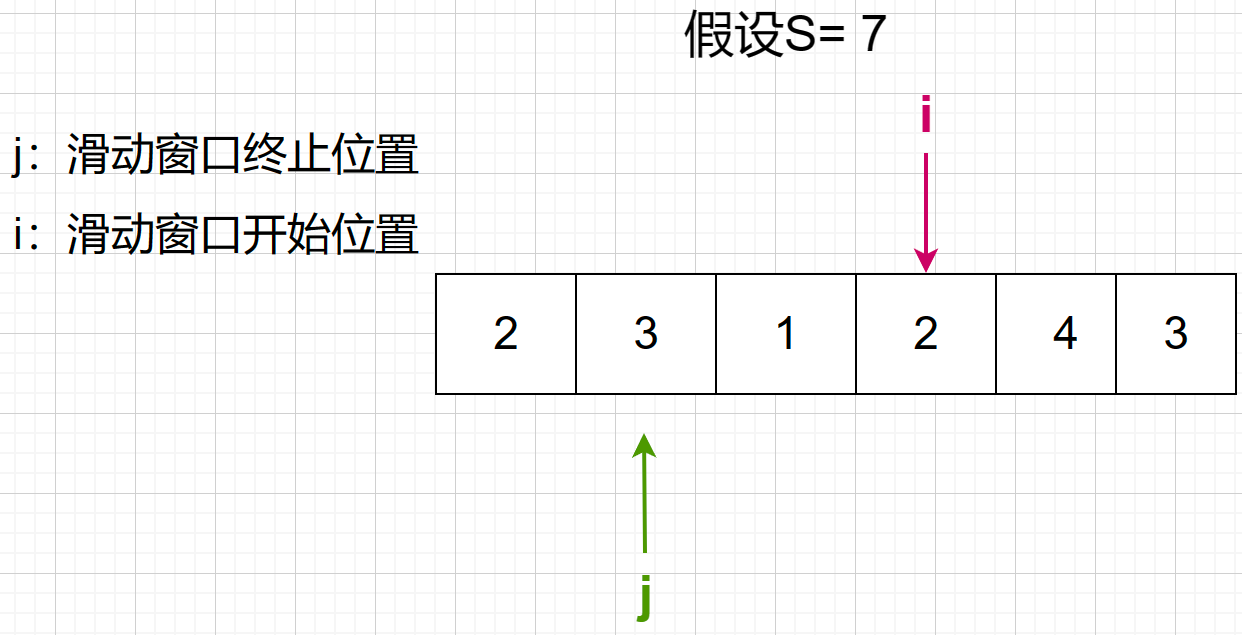
第四步,此时滑动窗口已不再大于等于7了,i就可以继续向右走了
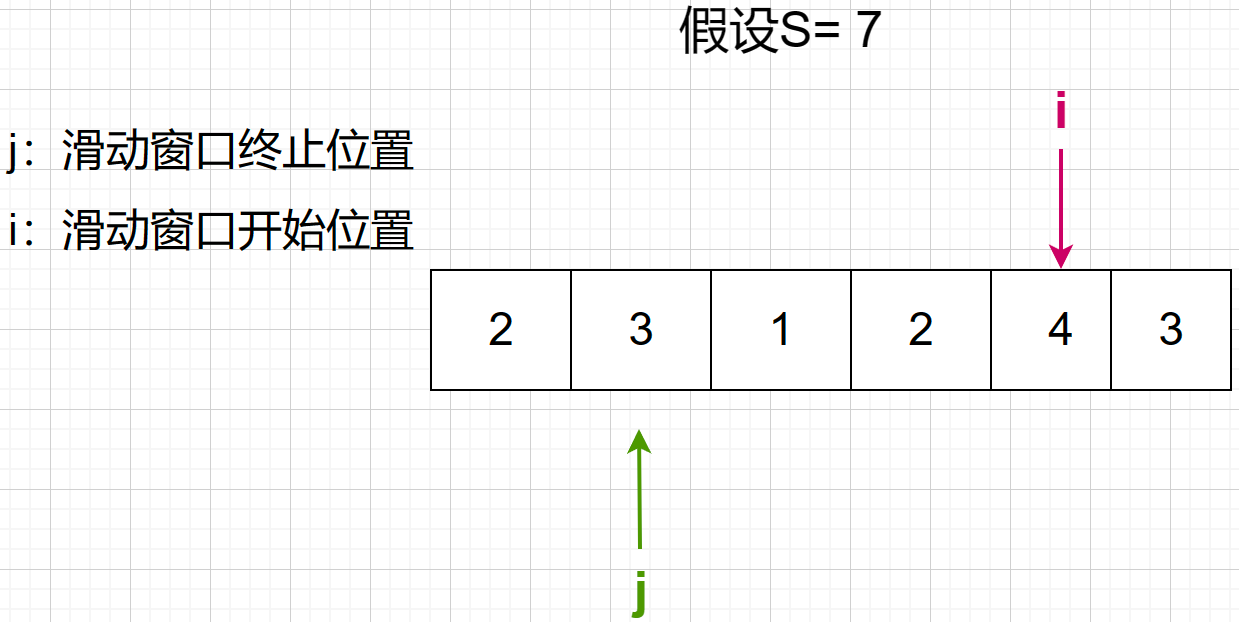
第五步,此时,滑动窗口已经大于等于7了,j就向右移到滑动窗口不大于等于7的位置就可以了,会发现1 + 2 + 4 = 7,需要继续向右走 ,长度为3
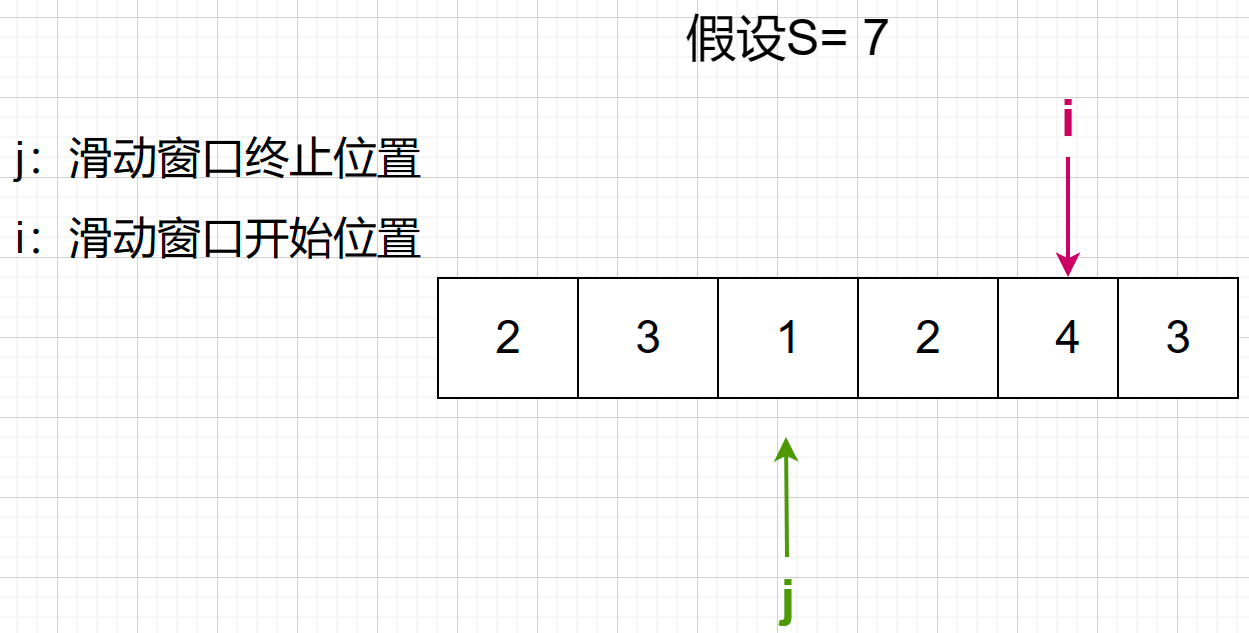
2 + 4 < 7,j停止走动

第六步,滑动窗口不再大于等于7了,i继续向右走

第七步,滑动窗口已大于等于7了,2 + 4 + 3 = 9 < 7 ,长度为3 , j继续向下移动
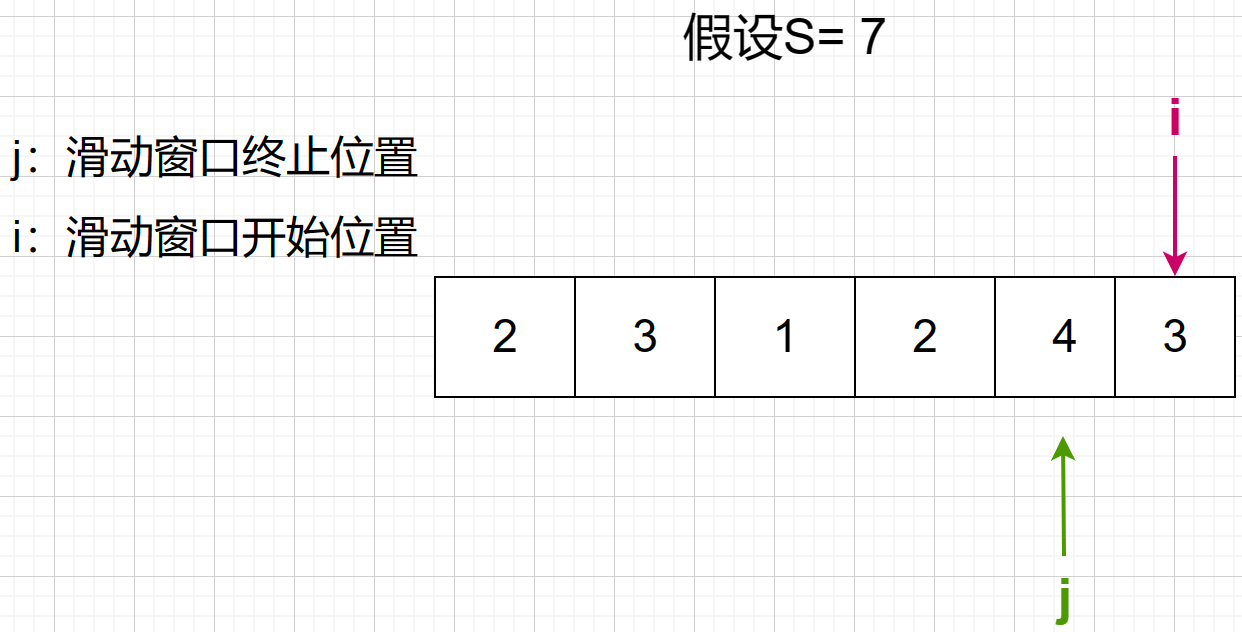
最后找到 4,3 ,长度为2, 是最短距离。
其实从动画中可以发现**滑动窗口也可以理解为双指针法的一种!**只不过这种解法更像是一个窗口的移动,所以叫做滑动窗口更适合一些。
在本题中实现滑动窗口,主要确定如下三点:
- 窗口内是什么?
- 如何移动窗口的起始位置?
- 如何移动窗口的结束位置?
窗口就是 满足其和 ≥ s 的长度最小的 连续 子数组。
窗口的起始位置如何移动:如果当前窗口的值大于s了,窗口就要向前移动了(也就是该缩小了)。
窗口的结束位置如何移动:窗口的结束位置就是遍历数组的指针,也就是for循环里的索引。
解题的关键在于 窗口的起始位置如何移动,如图所示:
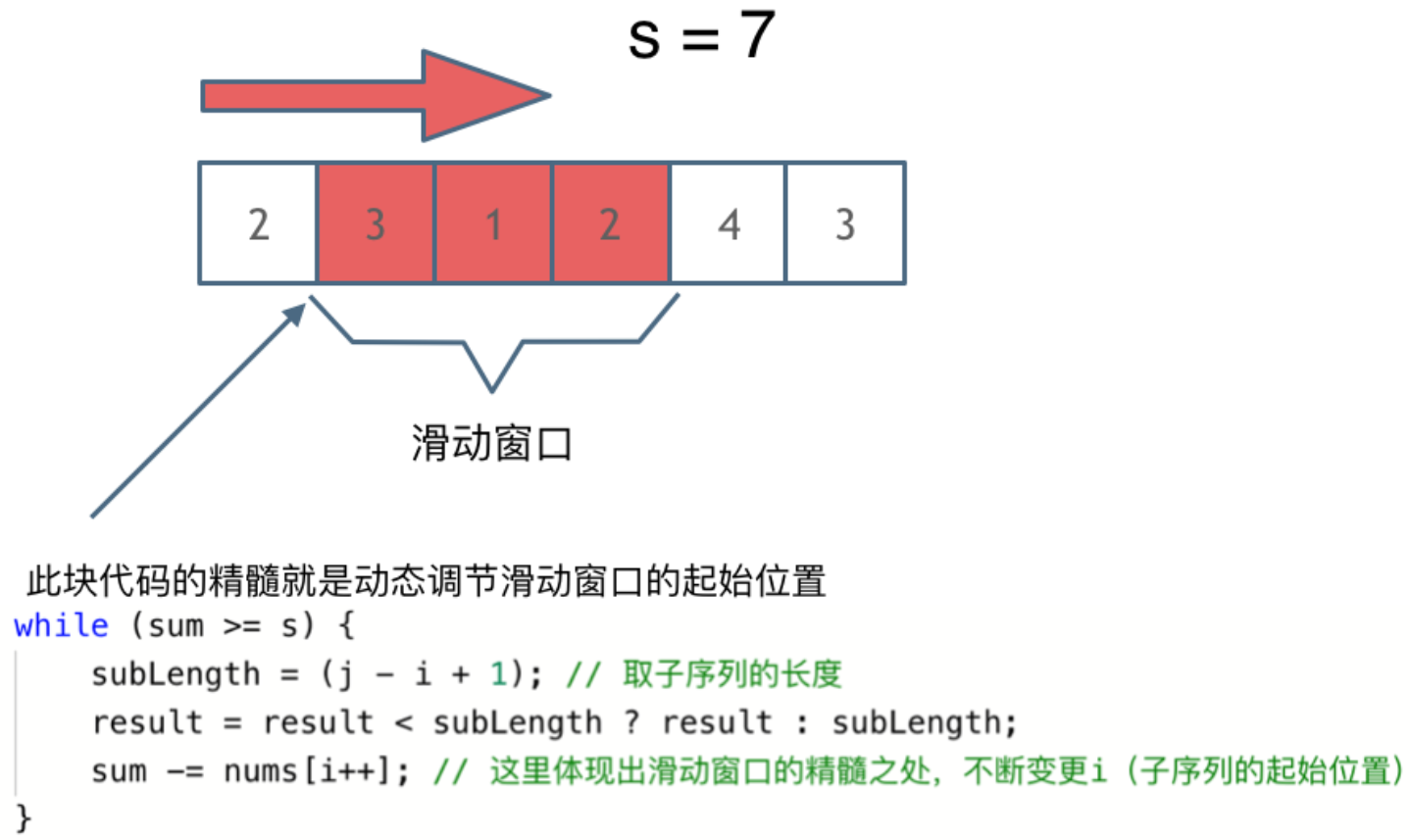
可以发现滑动窗口的精妙之处在于根据当前子序列和大小的情况,不断调节子序列的起始位置。从而将O(n^2)暴力解法降为O(n)。
代码如下:
class Solution {/*** 使用滑动窗口方法来找到最小长度的子数组* s 目标值*nums 正整数数组*return 最小长度的子数组的长度*/public int minSubArrayLen(int s, int[] nums) {int left = 0; // 左指针int sum = 0; // 当前滑动窗口的和int result = Integer.MAX_VALUE; // 最小长度,默认为最大值for (int right = 0; right < nums.length; right++) { // 右指针遍历数组sum += nums[right]; // 将当前元素加入滑动窗口的和while (sum >= s) { // 当滑动窗口的和大于等于目标值result = Math.min(result, right - left + 1); // 更新最小长度sum -= nums[left++]; // 左指针右移,从滑动窗口的和中减去左边界的元素}}return result == Integer.MAX_VALUE ? 0 : result; // 返回最小长度,如果不存在满足条件的子数组,则返回0}
}
- 时间复杂度:O(n)
- 空间复杂度:O(1)
一些录友会疑惑为什么时间复杂度是O(n)。
不要以为for里放一个while就以为是O(n^2)啊, 主要是看每一个元素被操作的次数,每个元素在滑动窗后进来操作一次,出去操作一次,每个元素都是被操作两次,所以时间复杂度是 2 × n 也就是O(n)。
两种方法的区别
暴力解法和滑动窗口方法之间的区别如下:
- 暴力解法:
- 暴力解法是一种简单直接的方法,在给定数组中遍历所有可能的连续子数组,计算它们的和,然后找到满足和大于等于目标值s的最小长度。
- 具体操作是使用两个嵌套的for循环,外层循环遍历所有可能的起始位置,内层循环遍历以当前起始位置为起点的所有连续子数组。
- 对于每个子数组,计算它们的和并与目标值s进行比较。如果和大于等于目标值s,则更新最小长度。
- 这种方法的时间复杂度为O(n^2),因为需要遍历所有可能的子数组。在最坏的情况下,数组中可能会有n个连续子数组。
- 空间复杂度为O(1),因为只使用了常数级别的额外空间。
- 滑动窗口方法:
- 滑动窗口方法使用两个指针来构建滑动窗口,左指针和右指针分别表示滑动窗口的左边界和右边界。
- 首先,将左指针和右指针都指向数组的第一个元素。
- 然后,移动右指针,将元素逐个加到滑动窗口的和中,直到滑动窗口的和大于等于目标值s为止。
- 当滑动窗口的和大于等于目标值s时,记录当前滑动窗口的长度,并更新最小长度。
- 然后,移动左指针,将滑动窗口的左边界向右移动一位,并从滑动窗口的和中减去左边界的元素。
- 重复上述步骤,直到右指针达到数组的末尾。
- 这种方法的时间复杂度为O(n),因为每个元素最多被访问两次(左指针和右指针),没有遍历所有可能的子数组。
- 空间复杂度为O(1),除了常数级别的几个变量外,没有使用额外的空间。
对于给定的示例输入s = 7, nums = [2,3,1,2,4,3],滑动窗口方法可以在O(n)的时间复杂度内找到满足条件的最小长度子数组,而暴力解法则需要O(n^2)的时间复杂度。因此,滑动窗口方法更高效。
总结
- 使用滑动窗口方法可以解决这个问题。定义两个指针,分别表示滑动窗口的左右边界。
- 初始化左指针和右指针都指向数组的第一个元素。
- 然后,移动右指针,将元素逐个加到滑动窗口的和中,直到滑动窗口的和大于等于目标值s为止。
- 当滑动窗口的和大于等于目标值s时,记录当前滑动窗口的长度,并更新最小长度。
- 然后,移动左指针,将滑动窗口的左边界向右移动一位,并从滑动窗口的和中减去左边界的元素。
- 重复步骤3到步骤5,直到右指针达到数组的末尾。
- 返回最小长度,如果不存在满足条件的子数组,则返回0。
- 时间复杂度分析:使用滑动窗口,每个元素最多会被访问两次(左指针和右指针),所以时间复杂度为O(n)。
- 空间复杂度分析:空间复杂度为O(1)。除了常数级别的几个变量外,没有使用额外的空间。
调用minSubArrayLen方法进行测试。将给定的数组nums和目标值s传递给方法,并将返回结果打印出来。预期输出为2,这是因为数组中的子数组[4, 3]的元素之和为7,且为满足条件的最小长度子数组。
测试代码:
package shuzhu;public class Day04 {public static int minSubArrayLen(int[] nums, int s) {int left = 0;int sum = 0;int result = Integer.MAX_VALUE;for(int right = 0;right < nums.length;right++){sum += nums[right];while(sum >= s){result = Math.min(result, right-left+1);sum -= nums[left++];}}return result == Integer.MAX_VALUE ? 0 : result;}public static void main(String[] args) {int[] nums = {2, 3, 1, 2, 4, 3};int s = 7;int result =minSubArrayLen(nums, s);System.out.println("长度最小的连续数组其长度为:"+result);}
}return result == Integer.MAX_VALUE ? 0 : result;}public static void main(String[] args) {int[] nums = {2, 3, 1, 2, 4, 3};int s = 7;int result =minSubArrayLen(nums, s);System.out.println("长度最小的连续数组其长度为:"+result);}
}
相关文章:

代码随想录—力扣算法题:209长度最小的子数组.Java版(示例代码与导图详解)
版本说明 当前版本号[20230808]。 版本修改说明20230808初版 目录 文章目录 版本说明目录209.长度最小的子数组思路暴力解法滑动窗口 两种方法的区别总结 209.长度最小的子数组 力扣题目链接 更多内容可点击此处跳转到代码随想录,看原版文件 给定一个含有 n 个…...

81 | Python可视化篇 —— Seaborn数据可视化
Seaborn是Python中一个基于Matplotlib的高级数据可视化库,它提供了更简单的API和更美观的图形样式,适用于数据探索和展示。在本教程中,我们将介绍Seaborn的基本概念和用法,并通过一些示例演示如何使用Seaborn来创建各种图表和图形。 文章目录 1. 导入Seaborn库和数据2. 数据…...
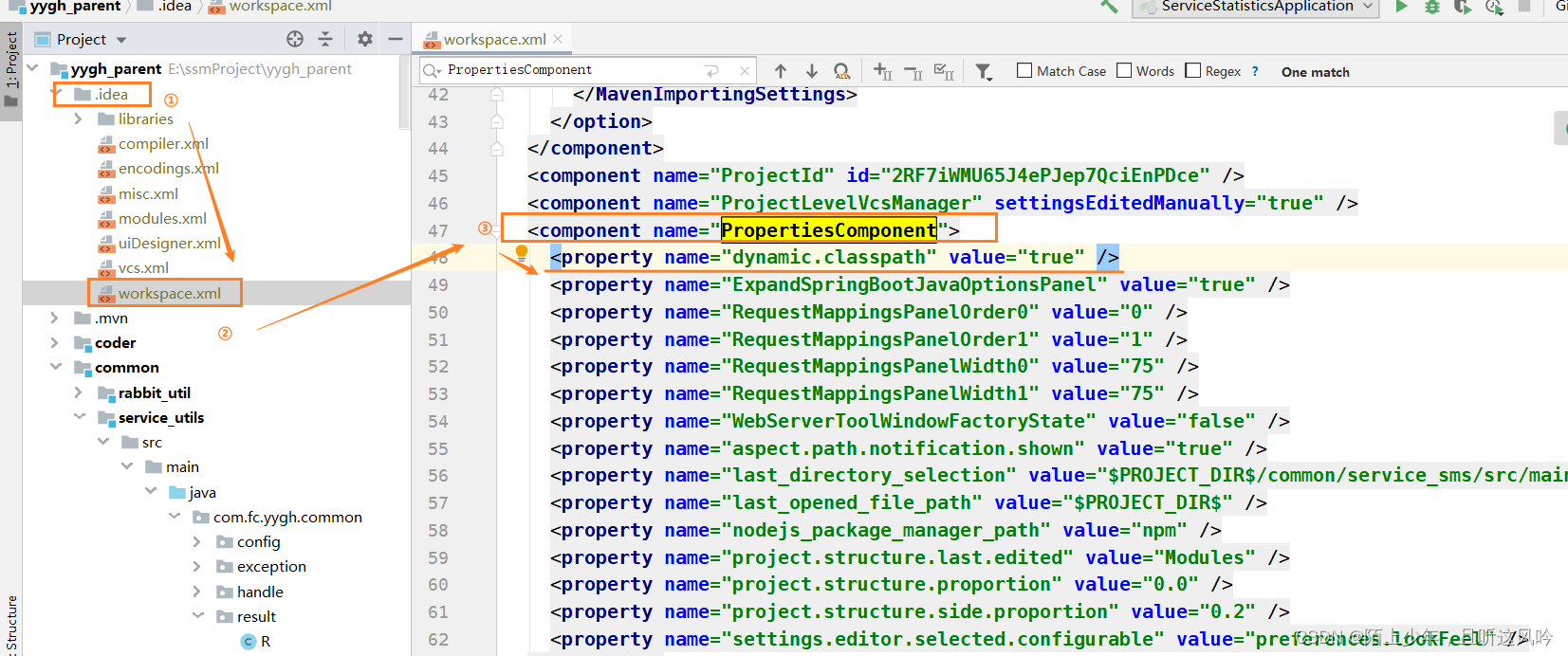
解决Error running XXXApplicationCommand line is too long.报错
测试IDEA版本:2019.2.4 ,2020.1.3 文章目录 一. 问题场景二. 报错原因2.1 为什么命令行过长会导致这种问题? 三. 解决方案3.1 方案一3.2 方案二 一. 问题场景 当我们从GitHub或公司自己搭建的git仓库上拉取项目代码时,会出现以下错误 报错代…...

【Linux】—— 进程等待 waitwaitpid
序言: 之前讲过,子进程退出,父进程如果不管不顾,就可能造成‘僵尸进程’的问题,进而造成内存泄漏。因此,为了解决这个问题,就需要用到有关 “进程等待” 的基本知识!!&am…...

el-tree 懒加载数据,增删改时局部刷新实现
1.数据过多时进行懒加载孩子节点,根据层级传参获取后端孩子数据 懒加载主要部分: 1参数: :load"loadNode" lazy :props"defaultProps" 2.defaultProps 需要设置isLeaf: isLeaf,去除最后一层孩子节点的展开图表 defaultProps: { ch…...
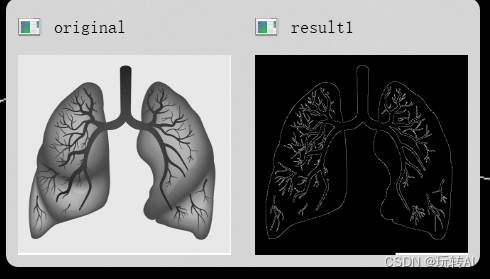
opencv基础44- Canny边缘检测详解-cv.Canny()
什么是Canny边缘检测? Canny边缘检测是一种经典的边缘检测算法,由John F. Canny在1986年提出。它被广泛应用于计算机视觉和图像处理领域,是一种多阶段的边缘检测算法,能够有效地检测图像中的边缘并抑制噪声。 Canny边缘检测的主要…...
--函数)
neo4j查询语言Cypher详解(三)--函数
函数 Cypher中的函数如果输入参数为null,则返回null。 以字符串作为输入的函数都对Unicode字符进行操作,而不是对标准字符进行操作。例如,size()函数应用于任何Unicode字符将返回1,即使该字符不适合一个字符的16位。 可以通过 …...

kafka权威指南(阅读摘录)
零复制 Kafka 使用零复制技术向客户端发送消息——也就是说,Kafka 直接把消息从文件(或者更确切地说是 Linux 文件系统缓存)里发送到网络通道,而不需要经过任何中间缓冲区。这是 Kafka 与其他大部分数据库系统不一样的地方&#…...
【爬虫实践】使用Python从网站抓取数据
一、说明 本周我不得不为客户抓取一个网站。我意识到我做得如此自然和迅速,分享它会很有用,这样你也可以掌握这门艺术。【免责声明:本文展示了我的抓取做法,如果您有更多相关做法请在评论中分享】 二、计划策略 2.1 策划 确定您…...
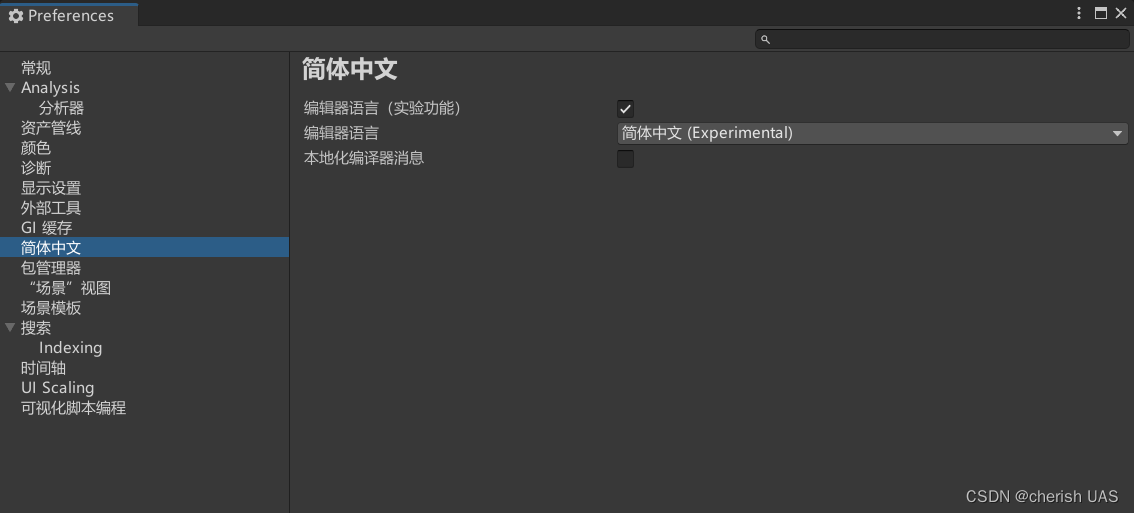
win10 2022unity设置中文
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言解决方法 前言 在Edit->preferences里找不到language选项。 解决方法 【1】打开下面地址 注意 :把{version}换成你当前安装的版本,比如说如果…...

python表白代码大全可复制,python表白代码大全简单
大家好,小编来为大家解答以下问题,python表白代码大全可复制,python表白程序代码完整版,现在让我们一起来看看吧! 今天是20230520,有人说:5代表的是人生五味,酸甜苦辣咸;…...

wordpress 打开缓慢处理
gravatar.com 头像网站被墙 追踪发现请求头像时长为21秒 解决方案一 不推荐,容易失效,网址要是要稳定为主,宁愿头像显示异常,也不能网址打不开 网上大部分搜索到的替换的CDN网址都过期了,例如:gravatar.du…...
Adobe ColdFusion 反序列化漏洞复现(CVE-2023-29300)
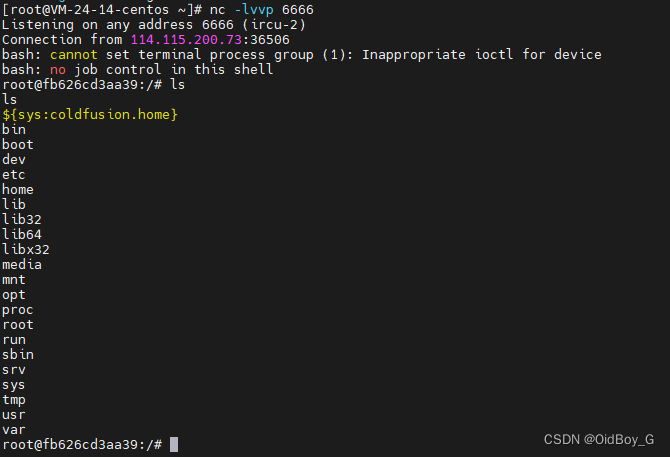
0x01 产品简介 Adobe ColdFusion是美国奥多比(Adobe)公司的一套快速应用程序开发平台。该平台包括集成开发环境和脚本语言。 0x02 漏洞概述 Adobe ColdFusion存在代码问题漏洞,该漏洞源于受到不受信任数据反序列化漏洞的影响,攻击…...

林【2018】
关键字: BST插入叶子结点、ADT结伴操作、队列插入前r-1、哈希函数二次探测法(1,-1,4,-4)、队列元素个数、折半查找失败次数、广义表链表结构、B-树构建、单链表指定位置插入数组元素 一、判断 二、单选 h(49)+1,-1,+4,-4...
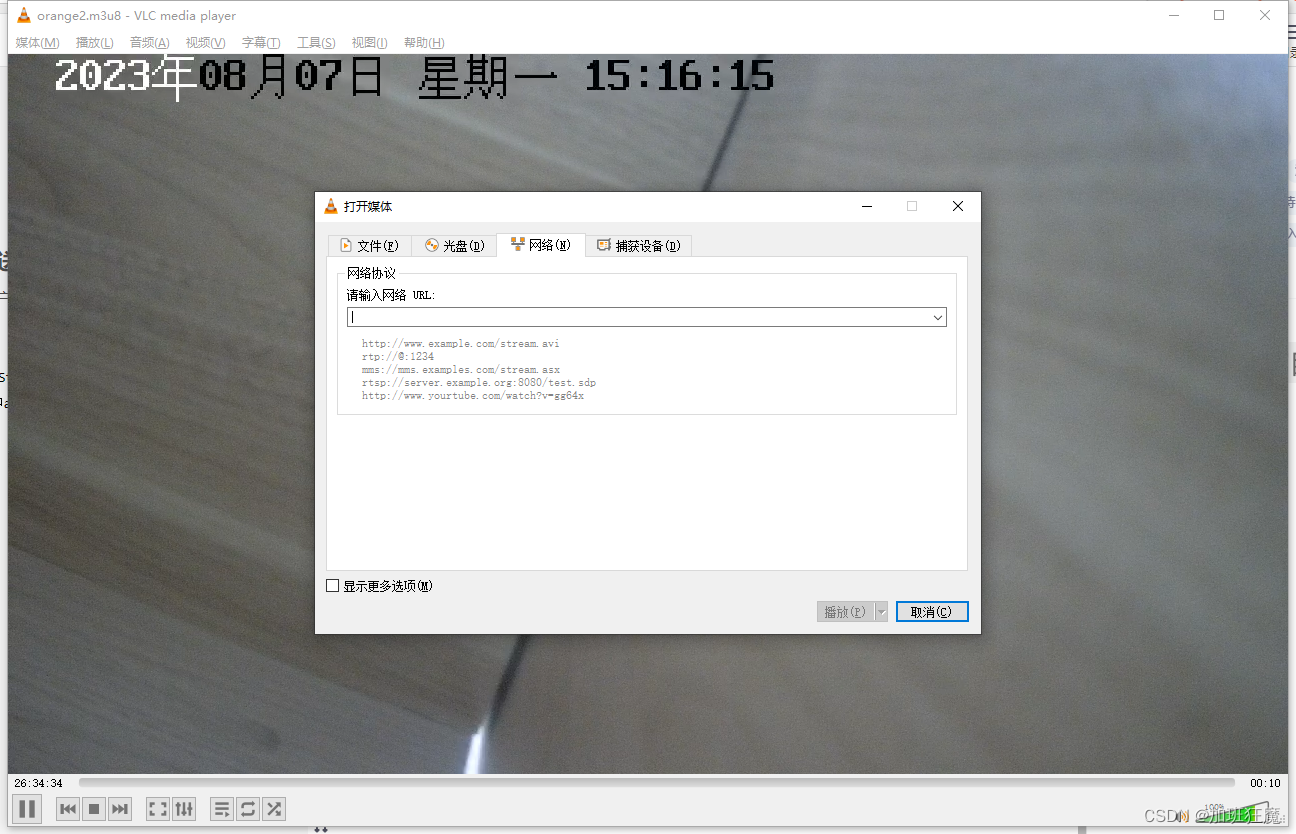
ffmpeg+nginx实现rtsp协议摄像头web端播放
ffmpegnginx实现rtsp协议摄像头web端播放 环境准备准备nginx环境添加rtmp模块添加hls转发 使用ffmpeg,将摄像头rtsp转为rtmp并推送到nginxVLC播放验证 环境准备 nginx(需要安装rtmp模块)ffmpeg 6.0vlc播放器(本地播放验证&#x…...

【周赛第69期】满分题解 软件工程选择题 枚举 dfs
目录 选择题1.2.3.4.面向对象设计七大原则 编程题S数最小H值 昨晚没睡好,脑子不清醒,痛失第1名 选择题 1. 关于工程效能,以下哪个选项可以帮助提高团队的开发效率? A、频繁地进行代码审查 B、使用自动化测试工具 C、使用版本控…...

P2015 二叉苹果树
P2015 二叉苹果树 类似于带限制背包问题,但不知道也能做。 n , q n,q n,q 范围小,大胆设 dp 状态。设 f u , i \large f_{u,i} fu,i 表示 u u u 子树内保留 i i i 根树枝的最大苹果数,可得状态转移方程 f u , i f u , j f v , i − …...

Linux 内核音频数据传递主要流程
Linux 用户空间应用程序通过声卡驱动程序(一般牵涉到多个设备驱动程序)和 Linux 内核 ALSA 框架导出的 PCM 设备文件,如 /dev/snd/pcmC0D0c 和 /dev/snd/pcmC0D0p 等,与 Linux 内核音频设备驱动程序和音频硬件进行数据传递。PCM 设…...

torch.device函数
torch.device 是 PyTorch 中用于表示计算设备(如CPU或GPU)的类。它允许你在代码中指定你希望在哪个设备上执行张量和模型操作,本文主要介绍了 torch.device 函数的用法和功能。 本文主要包含以下内容: 1.创建设备对象2.将张量和模…...
火车头采集器AI伪原创【php源码】
大家好,本文将围绕python作业提交什么文件展开说明,python123怎么提交作业是一个很多人都想弄明白的事情,想搞清楚python期末作业程序需要先了解以下几个事情。 火车头采集ai伪原创插件截图: I have a python project, whose fold…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...
