[LeetCode]1237. 找出给定方程的正整数解
题目链接:https://leetcode.cn/problems/find-positive-integer-solution-for-a-given-equation/description/
题目描述:
样例1:
输入:function_id = 1, z = 5
输出:[[1,4],[2,3],[3,2],[4,1]]
解释:function_id = 1 暗含的函数式子为 f(x, y) = x + y
以下 x 和 y 满足 f(x, y) 等于 5:
x=1, y=4 -> f(1, 4) = 1 + 4 = 5
x=2, y=3 -> f(2, 3) = 2 + 3 = 5
x=3, y=2 -> f(3, 2) = 3 + 2 = 5
x=4, y=1 -> f(4, 1) = 4 + 1 = 5
样例2:
输入:function_id = 2, z = 5
输出:[[1,5],[5,1]]
解释:function_id = 2 暗含的函数式子为 f(x, y) = x * y
以下 x 和 y 满足 f(x, y) 等于 5:
x=1, y=5 -> f(1, 5) = 1 * 5 = 5
x=5, y=1 -> f(5, 1) = 5 * 1 = 5
题目限定:

方法1:暴力枚举
func findSolution(customFunction func(int, int) int, z int) [][]int {res := make([][]int, 0, 100)for x := 1; x <= 1000; x++ {for y := 1; y<= 1000; y++ {if customFunction(x,y) == z {temp := []int{x, y}res = append(res,temp)}}}return res
}
暴力枚举法每次都从开始找y,x最多枚举1000次,而y每次也会枚举1000次,因此,总的复杂度为O(x*y)。
方法2:枚举+二分查找
func findSolution(customFunction func(int, int) int, z int) (res [][]int) {for x := 1; x <= 1000; x++ {l, r := 1, 1000for l <= r {mid := (l+r)/2if customFunction(x,mid) == z {res = append(res, []int{x,mid})break} else if customFunction(x,mid) > z {r = mid -1 } else {l = mid + 1}}}return res
}
既然我们知道y每次都从头开始找比较慢,那么我们可以优化y的查找时间,利用二分查找即可将找y的复杂度降到log级别,因此总的时间复杂度为O(xlogy)。
当然,golang中也可以使用sort库的Search方法:
func findSolution(customFunction func(int, int) int, z int) (res [][]int) {for x := 1; x <= 1000; x++ {y := 1 + sort.Search(999, func(y int) bool {return customFunction(x, y+1) >= z})if customFunction(x,y) == z {res = append(res, []int{x,y})}}return res
}
同时需要注意Search的用法,是从[0,n)去查找的,所以类似我们是从0-999中查找出来的下标,最后加上1就表示从1到1000了:
// Search uses binary search to find and return the smallest index i
// in [0, n) at which f(i) is true, assuming that on the range [0, n),
// f(i) == true implies f(i+1) == true. That is, Search requires that
// f is false for some (possibly empty) prefix of the input range [0, n)
// and then true for the (possibly empty) remainder; Search returns
// the first true index. If there is no such index, Search returns n.
// (Note that the “not found” return value is not -1 as in, for instance,
方法3:双指针
func findSolution(customFunction func(int, int) int, z int) (res [][]int) {y := 1000for x := 1; x <= 1000; x++ {for ; y > 0 ; y-- {if customFunction(x,y) < z {break}if customFunction(x,y) == z {res = append(res, []int{x,y})break}}}return res
}
这种方法关键在于直接利用函数单调递增的特性,一个答案从前往后找,另一个答案从后往前找,下一次寻找一定是基于上一次的结果,因此会少很多次遍历,x最多遍历1000次,y总的遍历次数也最多1000次,因此总的时间复杂度为O(x+y)。
相关文章:

[LeetCode]1237. 找出给定方程的正整数解
题目链接:https://leetcode.cn/problems/find-positive-integer-solution-for-a-given-equation/description/ 题目描述: 样例1: 输入:function_id 1, z 5 输出:[[1,4],[2,3],[3,2],[4,1]] 解释:functi…...

【路径规划】基于A*算法和Dijkstra算法的路径规划(Python代码实现)
👨🎓个人主页:研学社的博客💥💥💞💞欢迎来到本博客❤️❤️💥💥🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密…...

蓝桥杯 stm32 PWM 设置占空比
本文代码使用 HAL 库。 文章目录 前言一、创建CubeMX 工程 ,占空比分析:二、相关函数:1. 获取 CNT函数2.设置CNT为 0 函数(计算器清零)3.开启TIM2_CH1的输入捕获中断函数4.TIM 回调函数三、设置上升沿,下降沿四、在lcd上显示 R40 占空比 详细代码五、设置占空比,输出 PW…...
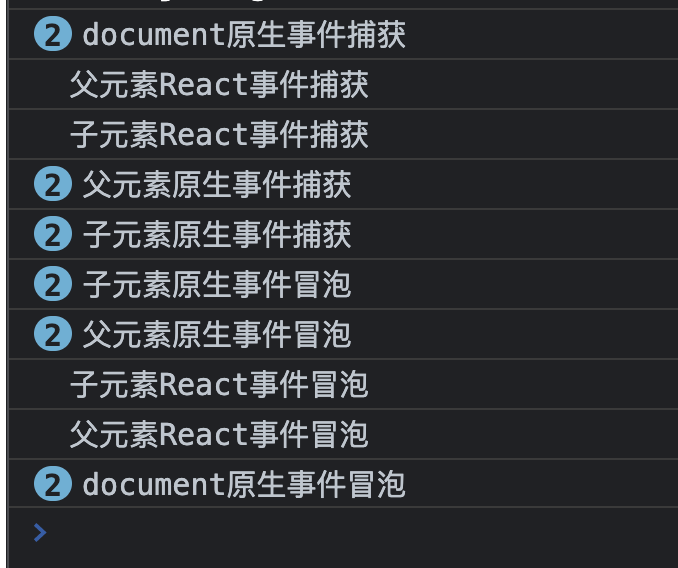
React 合成事件理解
1 事件三个阶段 捕获、目标、处理 (具体百度,后面有空补全)2import React from "react";class Test extends React.Component {parentRef;childRef;constructor(props) {super(props);this.parentRef React.createRef();this.chil…...

202302|读书笔记——国图点滴
杂志剪影|看一本赚一本系列 anywhere 随心而行随心而动,极简相生复古文艺 热情洋溢 色彩斑斓 极致优雅 深邃魅力 新生绽放 灿若星空 异彩纷呈含苞待放 惊艳绽放 爱在云端 空中婚礼 暗夜浪漫 策马逐梦橘影相映 浆果红唇 梦幻无暇 永无止境浮光掠影 微酥清风低调奢华…...

Linux 操作系统原理 — NUMA 架构中的多线程调度开销与性能优化
目录 文章目录 目录前言NUMA 架构中的多线程性能开销1、跨 Node 的 Memory 访问开销2、跨 Core 的多线程 Cache 同步开销3、多线程上下文切换开销4、多线程模式切换开销5、中断处理的开销6、TLB 缓存失效的开销7、内存拷贝的开销NUMA 架构中的性能优化:使用多核编程代替多线程…...
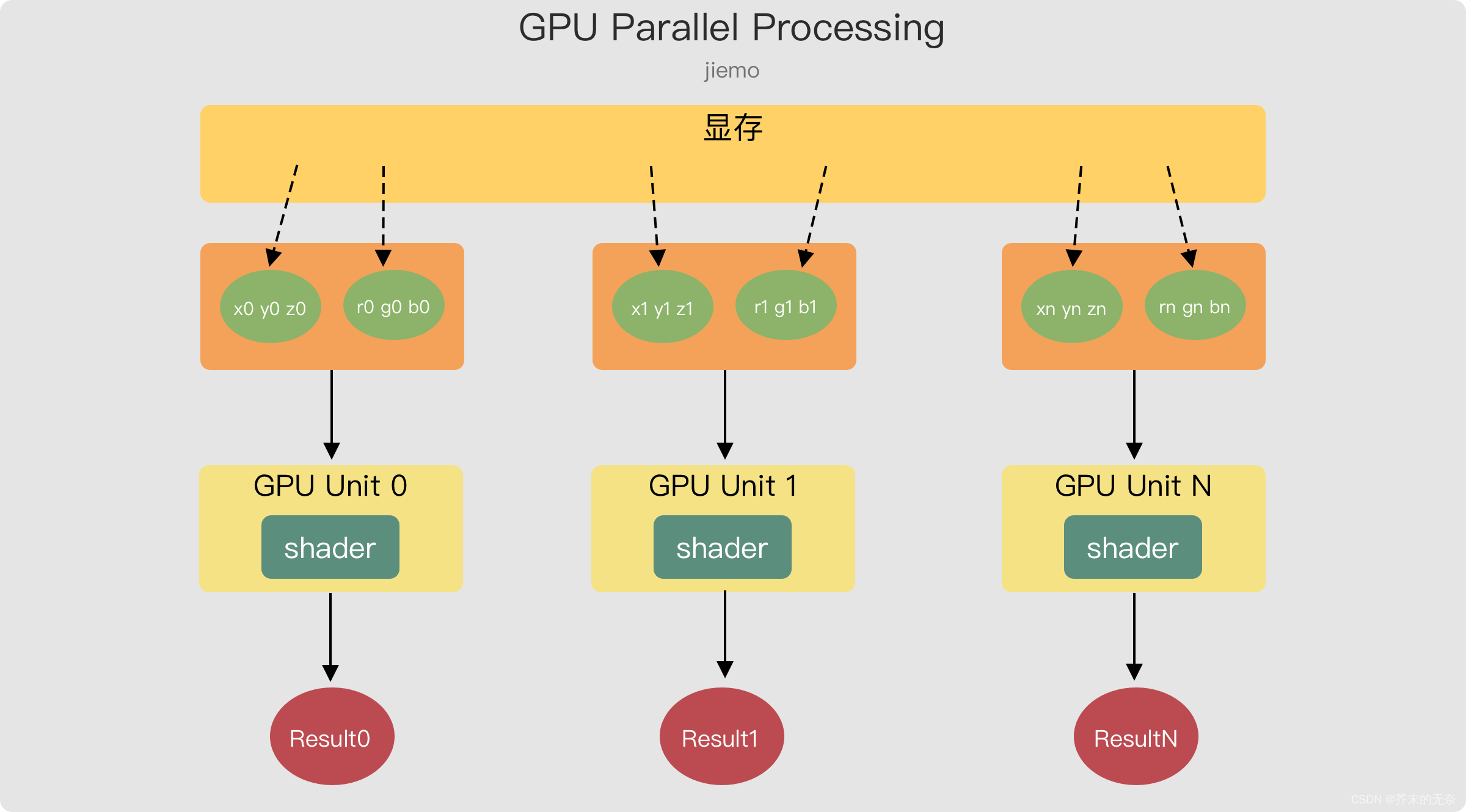
OpenGL - 如何理解 VAO 与 VBO 之间的关系
系列文章目录 LearnOpenGL 笔记 - 入门 01 OpenGLLearnOpenGL 笔记 - 入门 02 创建窗口LearnOpenGL 笔记 - 入门 03 你好,窗口LearnOpenGL 笔记 - 入门 04 你好,三角形 文章目录系列文章目录1. 前言2. 渲染管线的入口 - 顶点着色器2.1 顶点着色器处理过…...

Linux中sed的使用
语法: sed [选项] [sed内置命令字符] [输入文件]选项: 参数说明-n取消默认色的输出常与sed内置命令p一起使用-i直接将修改结果写入文件,不用-i,sed修改的是内存数据-e多次编译,不需要管道符了-r支持正则扩展 sed的内…...
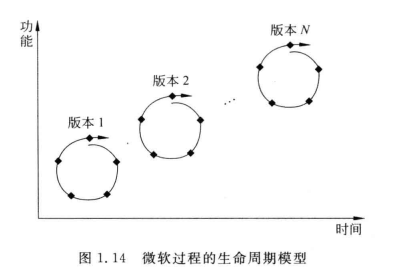
[软件工程导论(第六版)]第1章 软件工程学概述(复习笔记)
文章目录1.1 软件危机1.1.1 软件危机的介绍1.1.2 产生软件危机的原因1.1.3 消除软件危机的途径1.2 软件工程1.2.1 软件工程的介绍1.2.2 软件工程的基本原理1.2.3 软件工程方法学1.3 软件生命周期组成1.4 软件过程概念1.4.1 瀑布模型1.4.2 快速原型模型1.4.3 增量模型1.4.4 螺旋…...

ISP相关
Internet Service Provider,网络提供商/运营商,如电信、联通、移动等。 1. 与ISP互联的出口带宽 IDC或云提供商会与各运营商互联,互联的具体带宽数值一旦泄露,就会被恶意的攻击者利用。例如,若DDos攻击者知道了被攻击…...

vTESTstudio - VT System CAPL Functions - VT2004(续1)
成熟,就是某一个突如其来的时刻,把你的骄傲狠狠的踩到地上,任其开成花或者烂成泥。vtsStartStimulation - 启动激励输出功能:自动激励输出注意:在启动激励输出之前,一定要设置好输出模式Target:目标通道变量空间名称,例…...

WeakMap弱引用
let obj{name:张三} //{name:张三}这个对象能够被读取到,因为obj这个变量名对它的引用 //将引用覆盖掉 objnull //这个对象将会被从内存中移除,因为我们已经失去了对他的所有引用 let obj{name:张三} let arr[obj] objnull //对象{name:张三}不会…...
Springboot 使用quartz 定时任务 增删改查
前段时间公司项目用到了 定时任务 所以写了一篇定时任务的文章 ,浏览量还不错 , Springboot 整合定时任务 ) 所以就准备写第二篇, 如果你是一名Java工程师,你也可以会看到如下的页面 ,去添加定时任务 定时任务展示 :…...
 | 机试题+算法思路 【2023】)
华为OD机试 - 猜字谜(Python) | 机试题+算法思路 【2023】
最近更新的博客 华为OD机试 - 热点网络统计 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - 查找单入口空闲区域 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - 好朋友 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - 找出同班小朋友 | 备考思路,刷题要点…...
Linux常用命令汇总
1、tcpdump抓包 tcpdump这个命令是用来抓包的,默认情况下这个命令是没有的,需要安装一下: yum install -y tcpdump 使用这个命令的时候最好是加上你网卡的名称,不然可能使用不了: tcpdump -nn -i {网卡名称} 网卡名称…...
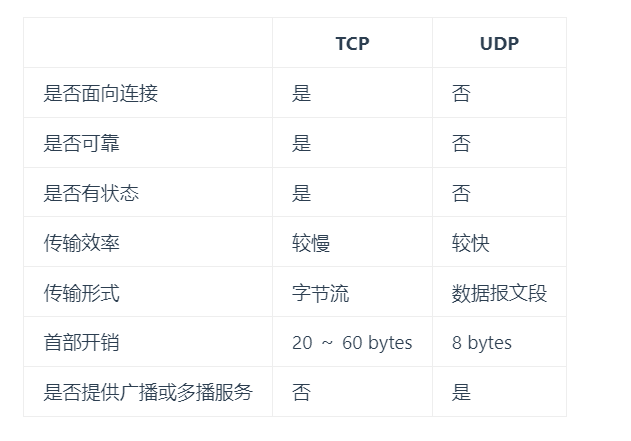
1.TCP、UDP区别、TCP/IP七层、四层模型、应用层协议(计网)
文章目录1.OSI 七层模型是什么?每一层的作用是什么?2.TCP/IP 四层模型是什么?每一层的作用是什么?应用层(Application layer)传输层(Transport layer)网络层(Network lay…...

气敏电阻的原理,结构,分类及应用场景总结
🏡《总目录》 目录 1,概述2,结构3,工作原理4,分类4.1,加热方式分类4.2,材料分类4.3,氧化还原分类5,应用场景6,总结1,概述 气敏电阻是指电阻值随着环境中某种气体的浓度变化而变化的电阻,本文对其工作原理,结构,分类和应用场景进行总结。 2,结构 气敏电阻由防爆…...

实验10 拓扑排序与最短路径2022
A. DS图—图的最短路径(无框架)题目描述给出一个图的邻接矩阵,输入顶点v,用迪杰斯特拉算法求顶点v到其它顶点的最短路径。输入第一行输入t,表示有t个测试实例第二行输入顶点数n和n个顶点信息第三行起,每行输…...

C/C++每日一练(20230218)
目录 1. 整数转罗马数字 2. 跳跃游戏 II 3. 买卖股票的最佳时机 IV 1. 整数转罗马数字 罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。 字符 数值 I 1 V 5 X …...
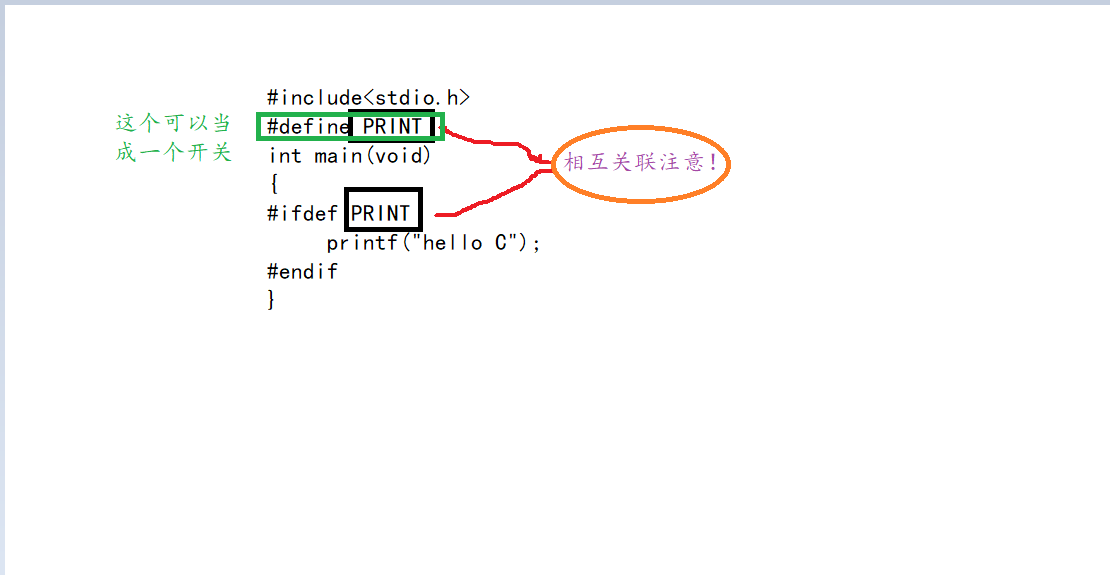
【C语言】预编译
🚩write in front🚩 🔎大家好,我是謓泽,希望你看完之后,能对你有所帮助,不足请指正!共同学习交流🔎 🏅2021年度博客之星物联网与嵌入式开发TOP5࿵…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...
