实验10 拓扑排序与最短路径2022
A. DS图—图的最短路径(无框架)
题目描述
给出一个图的邻接矩阵,输入顶点v,用迪杰斯特拉算法求顶点v到其它顶点的最短路径。
输入
第一行输入t,表示有t个测试实例
第二行输入顶点数n和n个顶点信息
第三行起,每行输入邻接矩阵的一行,以此类推输入n行
第i个结点与其它结点如果相连则为距离,无连接则为0,数据之间用空格隔开。
第四行输入一个顶点v,表示求该顶点v到其他顶点的最短路径距离
以此类推输入下一个示例
输出
对每组测试数据,输出:
每行输出顶点v到某个顶点的最短距离和最短路径
每行格式:顶点v编号-其他顶点编号-最短路径值----[最短路径]。没有路径输出:顶点v编号-其他顶点编号--1。具体请参考示范数据
输入:
2
5 0 1 2 3 4
0 5 0 7 15
0 0 5 0 0
0 0 0 0 1
0 0 2 0 0
0 0 0 0 0
0
6 V0 V1 V2 V3 V4 V5
0 0 10 0 30 100
0 0 5 0 0 0
0 0 0 50 0 0
0 0 0 0 0 10
0 0 0 20 0 60
0 0 0 0 0 0
V00-1-5----[0 1 ]
0-2-9----[0 3 2 ]
0-3-7----[0 3 ]
0-4-10----[0 3 2 4 ]
V0-V1--1
V0-V2-10----[V0 V2 ]
V0-V3-50----[V0 V4 V3 ]
V0-V4-30----[V0 V4 ]
V0-V5-60----[V0 V4 V3 V5 ]代码:
#include <iostream>
using namespace std;
#define INF 9999999
class graph {int vertex_num;string* vertex;//存储顶点int** edge;//存储矩阵边之间的长度bool* visited;string** path;//路径int* dest;//开始顶点到其它顶点的距离string startString;//开始顶点
public:graph() {}graph(int num, string* a, int** b, string start);void Dijkstra();void display();void show();
};void graph::show() {cout << "***************************" << endl;for (int i = 0; i < vertex_num; i++) {for (int j = 0; j < vertex_num; j++) cout << path[i][j];cout << endl;}
}
graph::graph(int num, string* a, int** b, string start) {vertex_num = num;startString = start;vertex = new string[vertex_num];edge = new int* [vertex_num];visited = new bool[vertex_num];dest = new int[vertex_num];path = new string * [vertex_num];for (int i = 0; i < vertex_num; i++) {visited[i] = false;vertex[i] = a[i];path[i] = new string[vertex_num];edge[i] = new int[vertex_num];for (int j = 0; j < vertex_num; j++) {edge[i][j] = b[i][j];path[i][j] ="";}}
}void graph::Dijkstra() {int start;for (int i = 0; i < vertex_num; i++) {if (vertex[i] == startString) {start = i;path[start][0] = "";break;}}for (int i = 0; i < vertex_num; i++) {if ((i != start) || edge[i] == 0) {dest[i] = INF;if ((edge[start][i] < INF) && edge[start][i] != 0) {dest[i] = edge[start][i];path[i][0] = vertex[start];path[i][1] = vertex[i];path[i][2] = "";}}}dest[start] = 0;visited[start] = true;int mindest = INF, currentVex = 0;for (int i = 0; i < vertex_num; i++) {mindest = INF;for (int j = 0; j < vertex_num; j++) {if (visited[j] == false) {if (dest[j] < mindest) {currentVex = j;mindest = dest[j];}}}int count = 0;visited[currentVex] = true;for (int j = 0; j < vertex_num; j++) {if ((visited[j] == false) && (mindest + edge[currentVex][j] < dest[j])) {dest[j] = mindest + edge[currentVex][j];for (count = 0; path[currentVex][count] != ""; count++)path[j][count] = path[currentVex][count];path[j][count++] = vertex[j];path[j][count] = "";}}}
}void graph::display() {int index;for (int i = 0; i < vertex_num; i++) if (vertex[i] == startString) index = i;for (int i = 0; i < vertex_num; i++) {if (vertex[i] != startString) {if (dest[i] ==INF) cout << startString << "-" << vertex[i] << "--1" << endl;else {cout << startString << "-" << vertex[i] << "-" <<dest[i] << "----[";for (int j = 0; path[i][j] != ""; j++) cout << path[i][j] << " ";cout << "]" << endl;}}}
}int main() {int t;cin >> t;while (t--) {int vertex_num;string* vertex, startString;int** edge;cin >> vertex_num;vertex = new string[vertex_num];edge = new int* [vertex_num];for (int i = 0; i < vertex_num; i++) {edge[i] = new int[vertex_num];cin >> vertex[i];}for (int i = 0; i < vertex_num; i++)for (int j = 0; j < vertex_num; j++) {cin >> edge[i][j];if (edge[i][j] == 0) edge[i][j] = INF;}cin >> startString;graph gp(vertex_num, vertex, edge, startString);int s = 0;gp.Dijkstra();gp.display();}
}B. 图综合练习--拓扑排序
题目描述
已知有向图,顶点从0开始编号,求它的求拓扑有序序列。
拓扑排序算法:给出有向图邻接矩阵
1.逐列扫描矩阵,找出入度为0且编号最小的顶点v
2.输出v,并标识v已访问
3.把矩阵第v行全清0
重复上述步骤,直到所有顶点输出为止
--程序要求--
若使用C++只能include一个头文件iostream;若使用C语言只能include一个头文件stdio
程序中若include多过一个头文件,不看代码,作0分处理
不允许使用第三方对象或函数实现本题的要求
输入
第一行输入一个整数t,表示有t个有向图
第二行输入n,表示图有n个顶点
第三行起,输入n行整数,表示图对应的邻接矩阵
以此类推输入下一个图的顶点数和邻接矩阵
输出
每行输出一个图的拓扑有序序列
输入:
2
5
0 1 0 1 1
0 0 1 0 0
0 0 0 0 1
0 0 1 0 0
0 0 0 0 0
7
0 0 0 0 0 0 0
1 0 1 1 0 0 0
1 0 0 0 0 0 0
1 0 1 0 0 0 0
0 0 0 0 0 1 1
0 1 0 0 0 0 0
0 0 0 1 0 1 0输出:
0 1 3 2 4
4 6 5 1 3 2 0 代码:
#include <iostream>
using namespace std;class Graph{int vexNum;int **matrix;bool *visit;int inDegreeZero();
public:Graph();~Graph();void TopSort();
};Graph::Graph() {cin>>vexNum;matrix = new int*[vexNum];visit = new bool[vexNum];for(int i=0;i<vexNum;i++){visit[i] = false;matrix[i] = new int[vexNum];for(int j=0;j<vexNum;j++)cin>>matrix[i][j];}
}Graph::~Graph() {delete visit;for(int i=0;i<vexNum;i++)delete []matrix[i];delete []matrix;
}void Graph::TopSort() {for(int k=0;k<vexNum;k++){int v=inDegreeZero();cout<<v<<' ';visit[v] = true;for(int i=0;i<vexNum;i++)matrix[v][i]=0;}cout<<endl;
}int Graph::inDegreeZero() {for(int col=0;col<vexNum;col++){bool flag= true;for(int row=0;row<vexNum;row++){if(matrix[row][col]!=0)flag= false;}if(flag && !visit[col])return col;}return -1;
}int main()
{int t;cin>>t;while (t--){Graph myGraph;myGraph.TopSort();}return 0;
}E. 拯救007
题目描述
在老电影“007之生死关头”(Live and Let Die)中有一个情节,007被毒贩抓到一个鳄鱼池中心的小岛上,他用了一种极为大胆的方法逃脱 —— 直接踩着池子里一系列鳄鱼的大脑袋跳上岸去!(据说当年替身演员被最后一条鳄鱼咬住了脚,幸好穿的是特别加厚的靴子才逃过一劫。)
设鳄鱼池是长宽为100米的方形,中心坐标为 (0, 0),且东北角坐标为 (50, 50)。池心岛是以 (0, 0) 为圆心、直径15米的圆。给定池中分布的鳄鱼的坐标、以及007一次能跳跃的最大距离,你需要告诉他是否有可能逃出生天。
输入
首先第一行给出两个正整数:鳄鱼数量 N(≤100)和007一次能跳跃的最大距离 D。随后 N 行,每行给出一条鳄鱼的 (x,y) 坐标。注意:不会有两条鳄鱼待在同一个点上。
输出
如果007有可能逃脱,就在一行中输出"Yes",否则输出"No"。
输入:
14 20
25 -15
-25 28
8 49
29 15
-35 -2
5 28
27 -29
-8 -28
-20 -35
-25 -20
-13 29
-30 15
-35 40
12 12输出:
Yes代码:
#include<iostream>
#include<math.h>
using namespace std;double x[200], y[200], vis[200];
double n, m, flag = 0;int DFS(int x1, int y1)
{if (abs(abs(x1) - 50) <= m || abs(abs(y1) - 50) <= m)//其绝对值小于mreturn flag = 1;for (int i = 0; i < n; i++){if (!vis[i] && pow(x1 - x[i], 2) + pow(y1 - y[i], 2) <= m * m)vis[i] = 1, DFS(x[i], y[i]), vis[i] = 0;}return 0;
}int main()
{cin >> n >> m;for (int i = 0; i < n; i++)cin >> x[i] >> y[i];if (m + 7.5 >= 50) flag = 1;for (int i = 0; i < n; i++){if (pow(x[i], 2) + pow(y[i], 2) <= (m + 7.5) * (m + 7.5)){vis[i] = 1;DFS(x[i], y[i]);vis[i] = 0;}}if (flag) cout << "Yes" << endl;else cout << "No" << endl;return 0;
}F. 货币套汇(图路径)
题目描述
套汇是指利用货币汇兑率的差异将一个单位的某种货币转换为大于一个单位的同种货币。例如,假定1 美元可以买0.7 英镑,1 英镑可以买9.5 法郎,1法郎可以买到0.16美元。通过货币兑换,一个商人可以从1 美元开始买入,得到0.7×9.5×0.16=1.064美元,从而获得6.4%的利润。 给定n种货币c1 ,c2 ,... ,cn的有关兑换率,试设计一个有效算法,确定货币间是否存在套汇的可能性。
提示:判断图上是否出现正环,即环上所有的边相乘大于1
输入
第一行:测试数据组数
每组测试数据格式为:
第一行:正整数n (1< =n< =30),正整数m,分别表示n种货币和m种不同的货币兑换率。
2~n+1行,n种货币的名称。
n+2~n+m+1行,每行有3 个数据项ci,rij 和cj ,表示货币ci 和cj的兑换率为 rij。
输出
对每组测试数据,如果存在套汇的可能则输出YES
如果不存在套汇的可能,则输出NO。
输入:
2
3 3
USDollar
BritishPound
FrenchFranc
USDollar 0.5 BritishPound
BritishPound 10.0 FrenchFranc
FrenchFranc 0.21 USDollar
3 6
USDollar
BritishPound
FrenchFranc
USDollar 0.5 BritishPound
USDollar 4.9 FrenchFranc
BritishPound 10.0 FrenchFranc
BritishPound 1.99 USDollar
FrenchFranc 0.09 BritishPound
FrenchFranc 0.19 USDollar输出:
YES
NO代码:
#include <iostream>
#include<string>
using namespace std;#define MAX_NUM 20class AdjMatrix
{
private:double matrix[MAX_NUM][MAX_NUM];string vex[MAX_NUM];//顶点表int NodeNum;int ArcNum;int conn_num;double value; ///路径汇率乘积int flag; ///是否能套汇int Visit[MAX_NUM];void DFS(int v){int w, i, k;if (Visit[v] == 0)Visit[v] = 1;int* AdjVex = new int[NodeNum];for (i = 0; i < NodeNum; i++)AdjVex[i] = -1;k = 0; ///寻找其相邻的点for (i = 0; i < NodeNum; i++){if (matrix[v][i] != 0) {AdjVex[k] = i;k++;}}i = 0;for (w = AdjVex[0]; w != -1; w = AdjVex[i]){ ///访问其所有相邻的点if (Visit[w] == 0){value = value * matrix[v][w];DFS(w);}else if (Visit[w] == 2) //如果可以回到初始点形成环{double TempValue = value; //判定边乘积是否大于1TempValue = TempValue * matrix[v][w];if (TempValue > 1.0){flag = 1;}}i++;}delete[]AdjVex;}public:AdjMatrix(int n){NodeNum = n;conn_num = 0;flag = 0;}~AdjMatrix() {}int Index(string s){for (int i = 0; i < NodeNum; i++){if (vex[i] == s)return i;}return -1;}void getMatrix(){for (int i = 0; i < NodeNum; i++)for (int j = 0; j < NodeNum; j++)matrix[i][j] = 0;//初始化矩阵cin >> ArcNum;for (int i = 0; i < NodeNum; i++){string s1;cin >> s1;vex[i] = s1;}for (int i = 0; i < ArcNum; i++){string s1, s2;double currency;int num1, num2;cin >> s1;cin >> currency;cin >> s2;num1 = Index(s1);num2 = Index(s2);matrix[num1][num2] = currency;}}void print(){int i, j;for (i = 0; i < NodeNum; i++){ ///输出点cout << vex[i];if (i != NodeNum - 1)cout << "\t";}cout << endl;for (i = 0; i < NodeNum; i++){for (j = 0; j < NodeNum; j++){cout << matrix[i][j];if (j != NodeNum - 1)cout << "\t";}cout << endl;}}void DFS(){int v, k;int i;for (k = 0; k < NodeNum; k++){int counter = 0;value = 1.0;v = k;for (i = 0; i < NodeNum; i++){if (i == v)Visit[i] = 2; ///表示起始点elseVisit[i] = 0;}do{if (Visit[v] == 0 || Visit[v] == 2){counter++;if (counter > 1) break; //表示从该点出发无法形成环,直接跳过DFS(v);}v = (v + 1) % NodeNum;} while (v != k);}if (flag == 1)cout << "YES";elsecout << "NO";cout << endl;}
};int main()
{int t;cin >> t;while (t--){int n;cin >> n;AdjMatrix mymatrix(n);mymatrix.getMatrix();mymatrix.DFS();}return 0;
}相关文章:

实验10 拓扑排序与最短路径2022
A. DS图—图的最短路径(无框架)题目描述给出一个图的邻接矩阵,输入顶点v,用迪杰斯特拉算法求顶点v到其它顶点的最短路径。输入第一行输入t,表示有t个测试实例第二行输入顶点数n和n个顶点信息第三行起,每行输…...

C/C++每日一练(20230218)
目录 1. 整数转罗马数字 2. 跳跃游戏 II 3. 买卖股票的最佳时机 IV 1. 整数转罗马数字 罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。 字符 数值 I 1 V 5 X …...
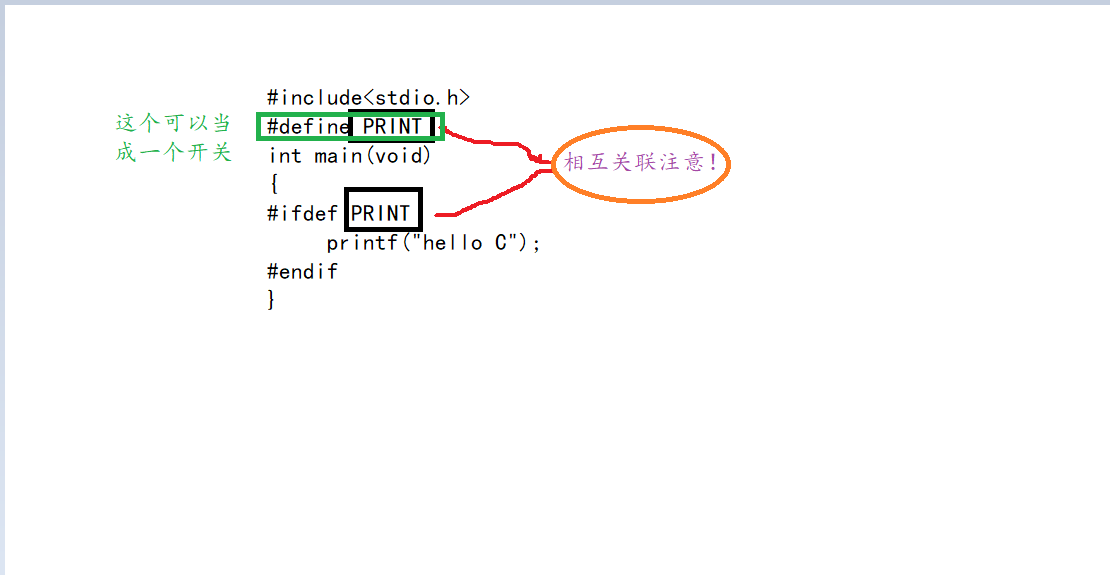
【C语言】预编译
🚩write in front🚩 🔎大家好,我是謓泽,希望你看完之后,能对你有所帮助,不足请指正!共同学习交流🔎 🏅2021年度博客之星物联网与嵌入式开发TOP5࿵…...
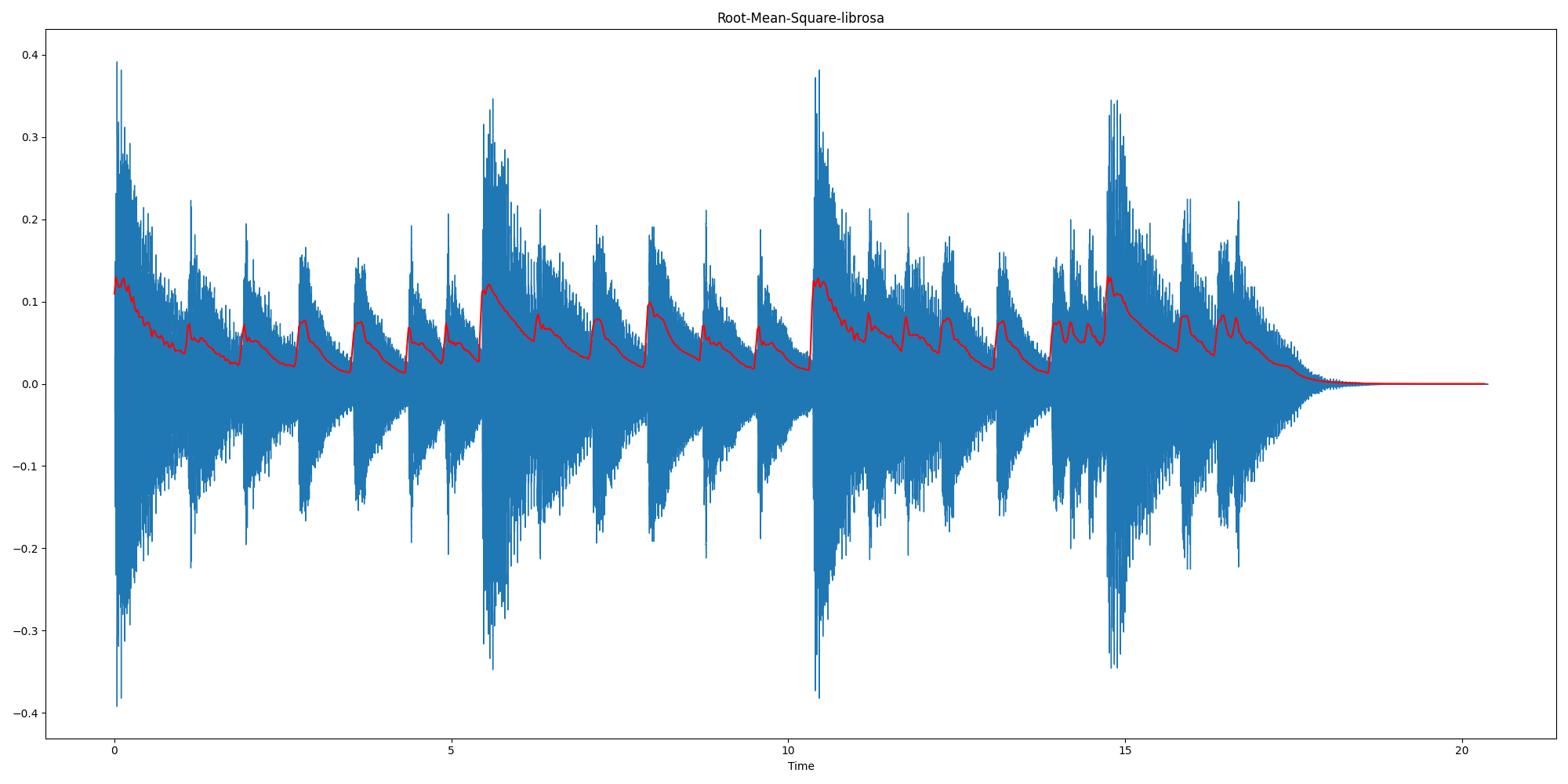
音频信号处理笔记(一)
相关课程:【音频信号处理及深度学习教程】 文章目录01 信号的时域分析1.1 分帧1.1.1 幅值包络1.1.2 均方根能量0 信号的叠加:https://teropa.info/harmonics-explorer/ 一个复杂信号分解成若干简单信号分量之和。不同个频率信号的叠加: 由于和差化积&a…...
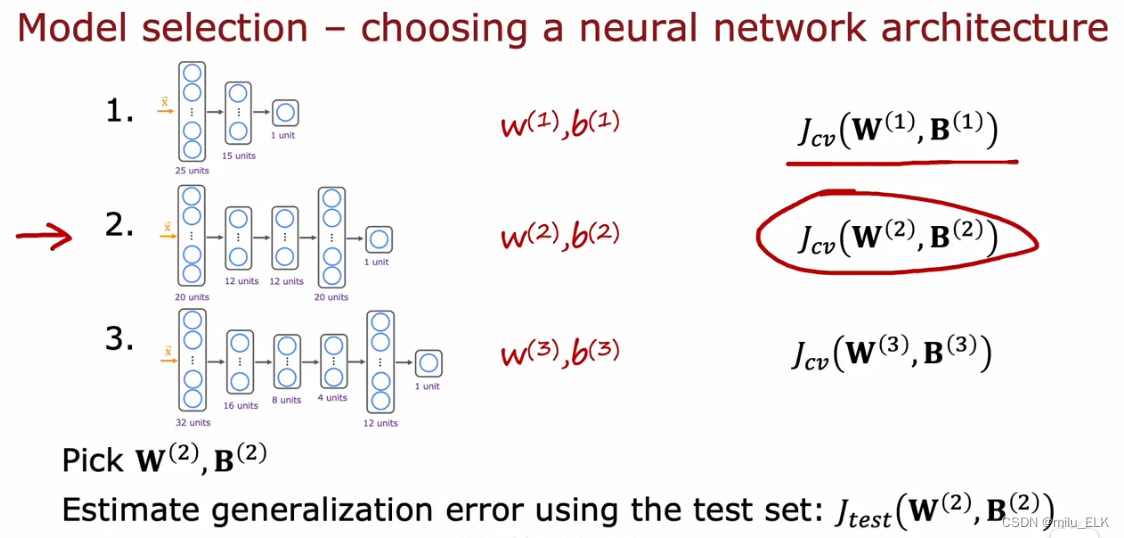
【深度学习】模型评估
上一章——多分类问题和多标签分类问题 文章目录算法诊断模型评估交叉验证测试算法诊断 如果你为问题拟合了一个假设函数,我们应当如何判断假设函数是否适当拟合了?我们可以通过观察代价函数的图像,当代价函数达到最低点的时候,此…...

AcWing《蓝桥杯集训·每日一题》—— 3777 砖块
AcWing《蓝桥杯集训每日一题》—— 3777. 砖块 文章目录AcWing《蓝桥杯集训每日一题》—— 3777. 砖块一、题目二、解题思路三、解题思路本次博客我是通过Notion软件写的,转md文件可能不太美观,大家可以去我的博客中查看:北天的 BLOG…...

CleanMyMac X软件下载及详细功能介绍
mac平台的知名系统清理应用CleanMyMac在经历了一段时间的测试后,全新设计的X正式上线。与CleanMyMac3相比,新版本的UI设计焕然一新,采用了完全不同的风格。使用Windows电脑时,很多人会下载各类优化软件,而在Mac平台中&…...

pytorch零基础实现语义分割项目(一)——数据概况及预处理
语义分割之数据加载项目列表前言数据集概况数据组织形式数据集划分数据预处理均值与方差结尾项目列表 语义分割项目(一)——数据概况及预处理 语义分割项目(二)——标签转换与数据加载 语义分割项目(三)…...

ARM+LINUX嵌入式学习路线
嵌入式学习是一个循序渐进的过程,如果是希望向嵌入式软件方向发展的话,目前最常见的是嵌入式Linux方向,关注这个方向,大概分3个阶段: 1、嵌入式linux上层应用,包括QT的GUI开发 2、嵌入式linux系统开发 3、…...
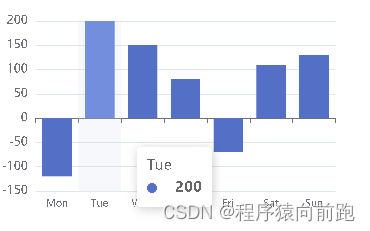
echart在微信小程序的使用
echart在微信小程序的使用 echarts不显示在微信小程序 <!-- 微信小程序的echart的使用 --> <view class"container"><ec-canvas id"mychart-dom-bar" canvas-id"mychart-bar" ec"{{ ec }}"></ec-canvas> &l…...
)
51单片机最强模块化封装(5)
文章目录 前言一、创建timer文件,添加timer文件路径二、timer文件编写三、模块化测试总结前言 今天这篇文章将为大家封装定时器模块,定时器是工程项目中必不可少的,希望大家能够将定时器理解清楚并且运用自如。 一、创建timer文件,添加timer文件路径 这里的操作就不过多…...

链表学习之判断链表是否回文
链表解题技巧 额外的数据结构(哈希表);快慢指针;虚拟头节点; 判断链表是否回文 要求:时间辅助度O(N),空间复杂度O(1) 方法1:栈(不考虑空间复杂度) 遍历一…...
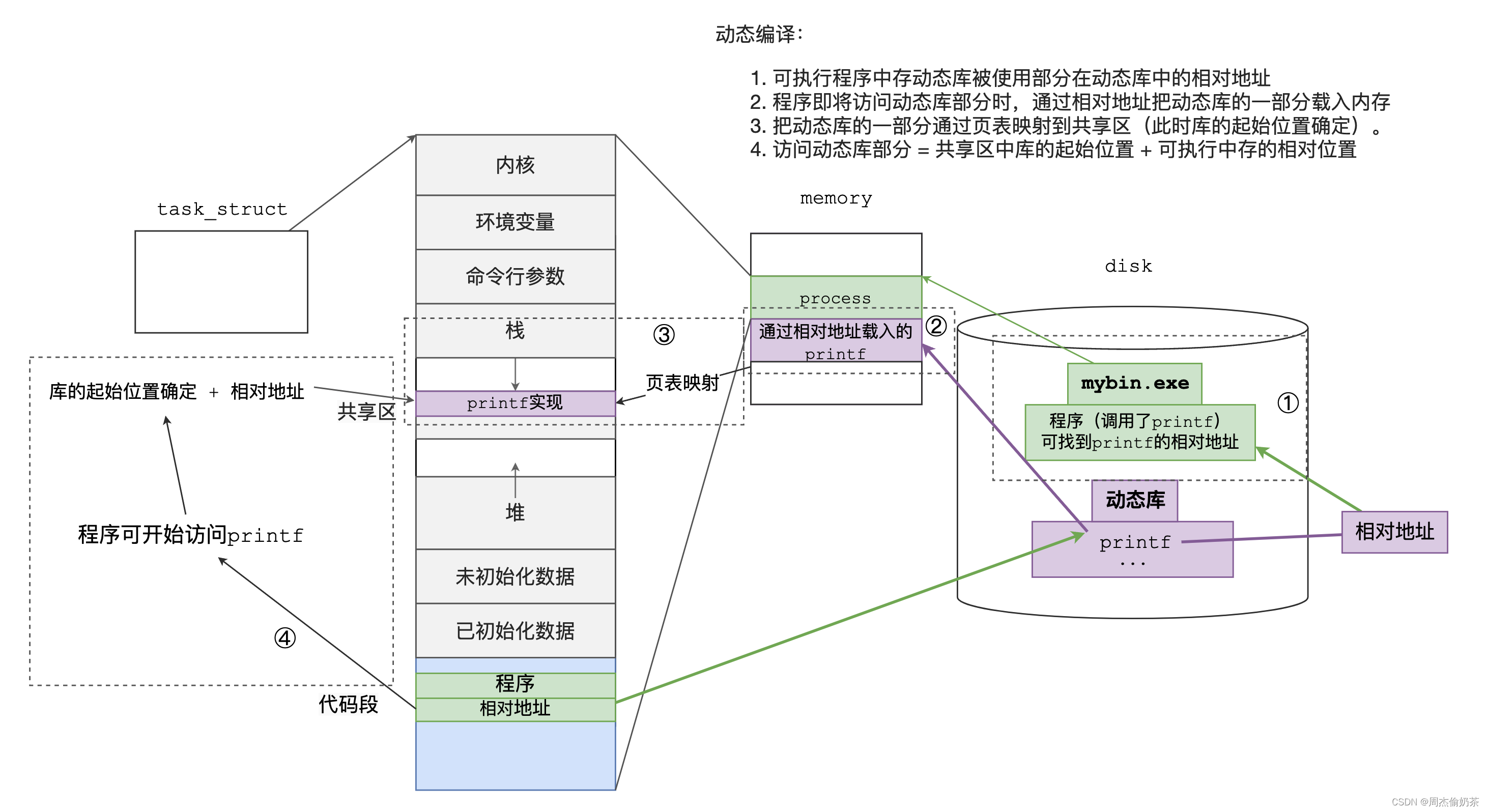
【Linux06-基础IO】4.5万字的基础IO讲解
前言 本期分享基础IO的知识,主要有: 复习C语言文件操作文件相关的系统调用文件描述符fd理解Linux下一切皆文件缓冲区文件系统软硬链接动静态库的理解和制作动静态编译 博主水平有限,不足之处望请斧正! C语言文件操作 #再谈文件…...

c++协程库理解—ucontext组件实践
文章目录1.干货写在前面2.ucontext初接触3.ucontext组件到底是什么4.小试牛刀-使用ucontext组件实现线程切换5.使用ucontext实现自己的线程库6.最后一步-使用我们自己的协程库1.干货写在前面 协程是一种用户态的轻量级线程 首先我们可以看看有哪些语言已经具备协程语义&#x…...

英语基础-状语
1. 课前引语 1. 形容词使用场景 (1). 放在系动词后面作表语 The boy is handsome. (2). 放在名词前面做定语 I like this beautiful girl. (3). 放在宾语后面做补语 You make your father happy. 总结:形容词无论做什么,都离不开名词,…...

目标检测笔记(八):自适应缩放技术Letterbox完整代码和结果展示
文章目录自适应缩放技术Letterbox介绍自适应缩放技术Letterbox流程自适应缩放Letterbox代码运行结果自适应缩放技术Letterbox介绍 由于数据集中存在多种不同和长宽比的样本图,传统的图片缩放方法按照固定尺寸来进行缩放会造成图片扭曲变形的问题。自适应缩放技术通…...

2023年全国最新高校辅导员精选真题及答案1
百分百题库提供高校辅导员考试试题、辅导员考试预测题、高校辅导员考试真题、辅导员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 一、选择题 11.李某与方某签订房屋租赁合同期间,李某欲购买租赁房屋ÿ…...

【Python】Python读写Excel表格
简要版,更多功能参考资料1。1 Excel文件保存格式基础概念此处不提,详见资料1。Excel的文件保存格式有两种: xls 和 xlsx。如果你看不到文件后缀,按下图设置可见。xls是Office 2003及之前版本的表格的默认保存格式。xlsx 是 Excel …...
Python每日一练(20230218)
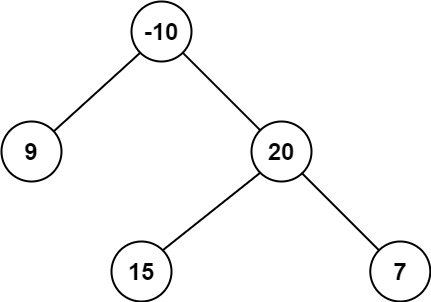
目录 1. 旋转图像 2. 解码方法 3. 二叉树最大路径和 1. 旋转图像 给定一个 n n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。 你必须在原地旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像…...
基于SSM框架的狼途汽车门店管理系统的设计与实现
基于SSM框架的狼途汽车门店管理系统的设计与实现 ✌全网粉丝20W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取项目下载方式🍅 一、…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...
