机器学习笔记之优化算法(十)梯度下降法铺垫:总体介绍
机器学习笔记之优化算法——梯度下降法铺垫:总体介绍
- 引言
- 回顾:线搜索方法
- 梯度下降方法整体介绍
引言
从本节开始,将介绍梯度下降法 ( Gradient Descent,GD ) (\text{Gradient Descent,GD}) (Gradient Descent,GD)。
回顾:线搜索方法
线搜索方法作为一种常见优化问题的策略,该方法的特点是:其迭代过程中,将数值解的方向和步长分开执行。对应数学符号表达如下:
其中P k \mathcal P_k Pk是一个向量,描述更新方向;α k \alpha_k αk是一个> 0 >0 >0的实数,表示步长。由于我们更关注向量P k \mathcal P_k Pk的方向性,因而通常将其表示为单位向量,即∣ ∣ P k ∣ ∣ = 1 ||\mathcal P_k|| = 1 ∣∣Pk∣∣=1。
x k + 1 = x k + α k ⋅ P k x_{k+1} = x_k + \alpha_k \cdot \mathcal P_k xk+1=xk+αk⋅Pk
线搜索方法的方向 P k \mathcal P_k Pk
在线搜索方法——方向角度中介绍过:关于目标函数 f ( ⋅ ) f(\cdot) f(⋅)的终极目标: min X ∈ R n f ( X ) \mathop{\min}\limits_{\mathcal X \in \mathbb R^n} f(\mathcal X) X∈Rnminf(X),如果数值解序列 { x k } k = 0 ∞ \{x_k\}_{k=0}^{\infty} {xk}k=0∞对应的目标函数结果 { f ( x k ) } k = 0 ∞ \{f(x_k)\}_{k=0}^{\infty} {f(xk)}k=0∞服从严格的单调性:
f ( x k + 1 ) < f ( x k ) f(x_{k+1}) < f(x_k) f(xk+1)<f(xk)
那么必然有:
其中[ ∇ f ( x k ) ] [\nabla f(x_k)] [∇f(xk)]表示数值解x k x_k xk对应目标函数的梯度向量,详细推导过程见上方链接。- P k \mathcal P_k Pk
化为单位向量产生的常数系数合并到α k \alpha_k αk中。
f ( x k + 1 ) − f ( x k ) ≈ [ ∇ f ( x k ) ] T P k ⋅ α k < 0 f(x_{k+1}) - f(x_k) \approx [\nabla f(x_k)]^T \mathcal P_k \cdot \alpha_k < 0 f(xk+1)−f(xk)≈[∇f(xk)]TPk⋅αk<0
从而将满足该条件的 P k \mathcal P_k Pk称作下降方向 ( Descent Direction ) (\text{Descent Direction}) (Descent Direction)。将上式展开有:
其中θ k \theta_k θk表示向量∇ f ( x k ) \nabla f(x_k) ∇f(xk)与向量P k \mathcal P_k Pk之间的夹角。在仅考虑方向角度对f ( x k + 1 ) − f ( x k ) f(x_{k+1}) - f(x_k) f(xk+1)−f(xk)影响的情况下,将α k \alpha_k αk忽略,不改变不等号方向。
∣ ∣ ∇ f ( x k ) ∣ ∣ ⋅ ∣ ∣ P k ∣ ∣ ⋅ cos θ k < 0 ||\nabla f(x_k)|| \cdot ||\mathcal P_k|| \cdot \cos \theta_k <0 ∣∣∇f(xk)∣∣⋅∣∣Pk∣∣⋅cosθk<0
其中 ∣ ∣ ∇ f ( x k ) ∣ ∣ , ∣ ∣ P k ∣ ∣ ||\nabla f(x_k)||,||\mathcal P_k|| ∣∣∇f(xk)∣∣,∣∣Pk∣∣均表示向量的模(均为固定的正值),因而 cos θ k ∈ [ − 1 , 0 ) \cos \theta_k \in [-1,0) cosθk∈[−1,0)。当 cos θ k = − 1 \cos \theta_k = -1 cosθk=−1时, f ( x k + 1 ) − f ( x k ) f(x_{k+1}) - f(x_k) f(xk+1)−f(xk)可取得最小值,从而达到最佳的优化方向。而此时下降方向 P k \mathcal P_k Pk与梯度方向 ∇ f ( x k ) \nabla f(x_k) ∇f(xk)方向相反。因此也称此时的 P k \mathcal P_k Pk为最速下降方向:
其中 ∣ ∣ ∇ f ( x k ) ∣ ∣ ||\nabla f(x_k)|| ∣∣∇f(xk)∣∣是关于上一次迭代结果 x k x_k xk的函数,因而是已知信息。
P k = − ∇ f ( x k ) \mathcal P_k = -\nabla f(x_k) Pk=−∇f(xk)
线搜索方法的步长 α k \alpha_k αk
关于当前迭代步骤的最优步长 α k \alpha_k αk通常有两种求解方式:
- 精确搜索:在 P k \mathcal P_k Pk固定的情况下,选择使得 f ( x k + 1 ) f(x_{k+1}) f(xk+1)达到最小的步长结果作为当前迭代步骤的最优步长:
其中x k , P k x_k,\mathcal P_k xk,Pk是确定的信息,因此可将f ( x k + 1 ) f(x_{k+1}) f(xk+1)视作关于α \alpha α的函数ϕ ( α ) \phi(\alpha) ϕ(α)。
α k = arg min α > 0 f ( x k + 1 ) = arg min α > 0 f ( x k + α ⋅ P k ) = arg min α > 0 ϕ ( α ) \begin{aligned}\alpha_k & = \mathop{\arg\min}\limits_{\alpha > 0} f(x_{k+1}) \\ & = \mathop{\arg\min}\limits_{\alpha > 0} f(x_k + \alpha \cdot \mathcal P_k) \\ & = \mathop{\arg\min}\limits_{\alpha > 0} \phi(\alpha) \end{aligned} αk=α>0argminf(xk+1)=α>0argminf(xk+α⋅Pk)=α>0argminϕ(α)
具体求解方式就是:对 α \alpha α求导,从而获取极值。但真实情况下,这种方式并不可取。关于目标函数f ( ⋅ ) f(\cdot) f(⋅)的复杂程度我们一无所知。关于梯度∇ f ( x k + α ⋅ P k ) \nabla f(x_k + \alpha \cdot \mathcal P_k) ∇f(xk+α⋅Pk)可能非常复杂。这仅仅是一次迭代步骤的解。也就是说:每次迭代都要求解精确解。这无疑增加了迭代的计算代价,我们仅希望迭代产生的步长能够收敛到lim k ⇒ ∞ f ( x k ) ⇒ f ∗ \mathop{\lim}\limits_{k \Rightarrow \infty}f(x_{k}) \Rightarrow f^* k⇒∞limf(xk)⇒f∗,它的中间过程是否准确并不在乎。
{ ∂ ϕ ( α ) ∂ α = ϕ ′ ( α ) = [ ∇ f ( x k + α ⋅ P k ) ] T P k ϕ ′ ( α ) = 0 ⇒ α k \begin{cases}\begin{aligned} & \frac{\partial \phi(\alpha)}{\partial \alpha} = \phi'(\alpha)= [\nabla f(x_k + \alpha \cdot \mathcal P_k)]^T \mathcal P_k \\ & \phi'(\alpha) = 0 \Rightarrow \alpha_k \end{aligned}\end{cases} ⎩ ⎨ ⎧∂α∂ϕ(α)=ϕ′(α)=[∇f(xk+α⋅Pk)]TPkϕ′(α)=0⇒αk
- 非精确搜索:相比于精确搜索,我们不计较迭代产生的步长结果是否最优,仅需要该结果能够帮助 f ( x k ) f(x_k) f(xk)有效收敛即可:
lim k ⇒ ∞ f ( x k ) ⇒ f ∗ \mathop{\lim}\limits_{k \Rightarrow \infty}f(x_{k}) \Rightarrow f^* k⇒∞limf(xk)⇒f∗
常见的非精确方法有: Armijo \text{Armijo} Armijo准则,对 Armijo \text{Armijo} Armijo准则进行优化的 Glodstein \text{Glodstein} Glodstein准则,以及基于 Armijo \text{Armijo} Armijo准则,对 Armijo,Glodstein \text{Armijo,Glodstein} Armijo,Glodstein准则进行优化的 Wolfe \text{Wolfe} Wolfe准则。
这里不再赘述。
梯度下降方法整体介绍
梯度下降法是一种典型的线搜索方法。并且它的更新方向 P k \mathcal P_k Pk就是最速下降方向: − ∇ f ( x k ) - \nabla f(x_k) −∇f(xk)。
梯度下降法也被称作最速下降法。这个最速下降方向仅仅是每一个迭代步骤中向量 x k x_k xk所在位置的最速下降方向,而不是全局最速下降方向。这与贪心算法类似,是一个局部最优。如下图:

很明显,蓝色实线是指本次迭代步骤中的最优方向;而蓝色虚线是指全局最优方向。上图描述的是二维权重特征对应的迭代过程。如果权重特征只有一维特征(一维向量;标量),对应图像表示如下:

此时函数关于x k x_k xk的梯度∇ f ( x k ) = [ f ′ ( x k ) ] 1 × 1 \nabla f(x_k) = [f'(x_k)]_{1 \times 1} ∇f(xk)=[f′(xk)]1×1,在迭代过程中寻找最优方向时,仅存在两个方向进行选择:沿着坐标轴与逆着坐标轴(红色箭头)。而此时f ′ ( x k ) > 0 f'(x_k) >0 f′(xk)>0,因而我们将数轴的正方向视作梯度方向;对应地,将数轴的反方向视作负梯度方向。针对当前的斜率信息,我们沿着负梯度方向更新到x k + 1 x_{k+1} xk+1。
关于梯度下降法的步长:
-
在后续过程中将介绍梯度下降法中如何求解精确步长,以及相应的限制条件。这里加一个传送门;
-
关于非精确搜索求解步长,这里补充一点关于各非精确搜索方法之间的一些逻辑上的关系。
在简单认识 Wolfe Condition \text{Wolfe Condition} Wolfe Condition的收敛性证明一节中介绍了使用 Zoutendijk \text{Zoutendijk} Zoutendijk定理,验证了作用于 Wolfe \text{Wolfe} Wolfe准则的步长结果可以使 { f ( x k ) } k = 1 ∞ \{f(x_k)\}_{k=1}^{\infty} {f(xk)}k=1∞收敛。但实际上: Zoutendijk \text{Zoutendijk} Zoutendijk定理同样可以作用于 Armijo,Glodstein \text{Armijo,Glodstein} Armijo,Glodstein准则,并证明其步长能够使 { f ( x k ) } k = 1 ∞ \{f(x_k)\}_{k=1}^{\infty} {f(xk)}k=1∞收敛。
由于 Wolfe \text{Wolfe} Wolfe准则是基于 Armijo \text{Armijo} Armijo准则提出的,其本质就是:在 Armijo \text{Armijo} Armijo准则的基础上,那些梯度结果 ∇ f ( x k + 1 ) \nabla f(x_{k+1}) ∇f(xk+1)过小的 ϕ ( α ) \phi(\alpha) ϕ(α)点对应的 α \alpha α通过参数 C 2 \mathcal C_2 C2消除掉了:
Armijo Condition : { ϕ ( α ) < f ( x k ) + C 1 ⋅ [ ∇ f ( x k ) ] T P k ⋅ α C 1 ∈ ( 0 , 1 ) Wolfe Condition : { ϕ ( α ) ≤ f ( x k ) + C 1 ⋅ [ ∇ f ( x k ) ] T P k ⋅ α ϕ ′ ( α ) ≥ C 2 ⋅ [ ∇ f ( x k ) ] T P k C 1 ∈ ( 0 , 1 ) C 2 ∈ ( C 1 , 1 ) \begin{aligned} & \text{Armijo Condition : }\begin{cases} \phi(\alpha) < f(x_k) + \mathcal C_1 \cdot [\nabla f(x_k)]^T \mathcal P_k \cdot \alpha \\ \quad \\ \mathcal C_1 \in (0,1) \end{cases} \\ & \text{Wolfe Condition : }\begin{cases} \phi(\alpha) \leq f(x_k) + \mathcal C_1 \cdot [\nabla f(x_k)]^T \mathcal P_k \cdot \alpha \\ \phi'(\alpha) \geq \mathcal C_2 \cdot [\nabla f(x_k)]^T \mathcal P_k \\ \mathcal C_1 \in (0,1) \\ \mathcal C_2 \in (\mathcal C_1,1) \end{cases} \end{aligned} Armijo Condition : ⎩ ⎨ ⎧ϕ(α)<f(xk)+C1⋅[∇f(xk)]TPk⋅αC1∈(0,1)Wolfe Condition : ⎩ ⎨ ⎧ϕ(α)≤f(xk)+C1⋅[∇f(xk)]TPk⋅αϕ′(α)≥C2⋅[∇f(xk)]TPkC1∈(0,1)C2∈(C1,1)
反过来说: Armijo \text{Armijo} Armijo准则相当于 Wolfe \text{Wolfe} Wolfe准则的一种极端情况:在 C 1 \mathcal C_1 C1确定划分边界的基础上,一个 α \alpha α都不去除,即: C 2 = 1 \mathcal C_2 = 1 C2=1。
同理, Glodstein \text{Glodstein} Glodstein准则也是 Wolfe \text{Wolfe} Wolfe准则中的一种情况。与 Armijo \text{Armijo} Armijo这种极端情况不同的是, Glodstein \text{Glodstein} Glodstein准则更像是一种取巧情况:在 C 1 ∈ ( 0 , 1 2 ) \begin{aligned}\mathcal C_1 \in \left(0,\frac{1}{2} \right)\end{aligned} C1∈(0,21)确定划分边界的基础上,选择一个合适的 C 2 ∈ ( 1 2 , 1 ) \begin{aligned}\mathcal C_2 \in \left(\frac{1}{2},1\right)\end{aligned} C2∈(21,1)使得斜率分别为 C 1 ⋅ [ ∇ f ( x k ) ] T P k \mathcal C_1 \cdot [\nabla f(x_k)]^T \mathcal P_k C1⋅[∇f(xk)]TPk和 C 2 ⋅ [ f ( x k ) ] T P k \mathcal C_2 \cdot [f(x_k)]^T \mathcal P_k C2⋅[f(xk)]TPk的直线关于斜率为 1 2 [ ∇ f ( x k ) ] T P k \begin{aligned}\frac{1}{2} [\nabla f(x_k)]^T \mathcal P_k\end{aligned} 21[∇f(xk)]TPk直线对称。
因为在C 1 ∈ ( 0 , 1 2 ) \mathcal C_1 \in \begin{aligned} \left(0,\frac{1}{2}\right)\end{aligned} C1∈(0,21)情况下,Wolfe \text{Wolfe} Wolfe准则关于C 2 \mathcal C_2 C2的描述范围( C 1 , 1 ) (\mathcal C_1,1) (C1,1)必然大于( 1 2 , 1 ) \begin{aligned}\left(\frac{1}{2},1\right)\end{aligned} (21,1)。因此必然能够找到这个合适的点,从而使该点情况下Wolfe \text{Wolfe} Wolfe准则等价于Glodstein \text{Glodstein} Glodstein准则。
关于梯度下降法的收敛速度:相比梯度下降法的收敛性,我们更关心在已知收敛的情况下,它的收敛速度情况。在上一节中对收敛速度进行了简单认识:
- 从收敛速度判别标准的角度划分,介绍了 Q \mathcal Q Q-收敛速度与 R \mathcal R R-收敛速度;
- 从收敛速度强度的角度划分(以 Q \mathcal Q Q-收敛速度为例),介绍了 Q \mathcal Q Q-次线性收敛/线性收敛/超线性收敛/二次收敛。
而在梯度下降法中,它的收敛速度取决于目标函数 f ( ⋅ ) f(\cdot) f(⋅)自身的性质:
-
关于目标函数 f ( ⋅ ) f(\cdot) f(⋅)的基础条件:向下有界,在定义域内可微(至少局部可微);
如果不可微,我们甚至没有办法求解梯度,更不要说梯度的更新了。 -
要求 f ( ⋅ ) f(\cdot) f(⋅)至少是局部凸函数,并且其梯度 ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅)必然服从利普希兹连续。而利普希兹连续的作用在于:目标函数梯度 ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅)的变化量被常数 L \mathcal L L限制住。或者说: ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅)的变化不会过于剧烈。
相反,如果不对 ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅)进行约束,很容易会出现梯度爆炸。因为可能存在:目标函数梯度可能在某一范围内飙升至极大。
在综上条件下,可达到次线性收敛级别的收敛速度。
在上述条件的基础上,如果 f ( ⋅ ) f(\cdot) f(⋅)是一个强凸函数 ( Strong Convex Function ) (\text{Strong Convex Function}) (Strong Convex Function),可达到线性收敛级别的收敛速度。
关于凸函数的强度性质:凸函数 < < <严格凸函数 < < <强凸函数。在后续进行介绍。传送门
在第二种条件的基础上:如果 f ( ⋅ ) f(\cdot) f(⋅)仍然是一个强凸函数,并且 f ( ⋅ ) f(\cdot) f(⋅)在其定义域内二阶可微,其对应的 Hession Matrix ∇ 2 f ( ⋅ ) \text{Hession Matrix} \nabla^2 f(\cdot) Hession Matrix∇2f(⋅)存在并满足:
其中L \mathcal L L依然是利普希兹连续中的具有限制作用的常数;≼ \preccurlyeq ≼表示矩阵小于等于;I \mathcal I I表示单位矩阵。关于∣ ∣ ∇ f ( x ) − ∇ f ( y ) ∣ ∣ ∣ ∣ x − y ∣ ∣ = ∇ 2 f ( ξ ) \begin{aligned}\frac{||\nabla f(x) - \nabla f(y)||}{||x - y||} = \nabla^2 f(\xi)\end{aligned} ∣∣x−y∣∣∣∣∇f(x)−∇f(y)∣∣=∇2f(ξ)详见拉格朗日中值定理。
∀ x , y ∈ R n : ∣ ∣ ∇ f ( x ) − ∇ f ( y ) ∣ ∣ ∣ ∣ x − y ∣ ∣ = ∇ 2 f ( ξ ) ≼ L ⋅ I \forall x,y \in \mathbb R^n :\begin{aligned}\frac{||\nabla f(x) - \nabla f(y)||}{||x - y||} = \nabla^2 f(\xi) \preccurlyeq \mathcal L \cdot \mathcal I \end{aligned} ∀x,y∈Rn:∣∣x−y∣∣∣∣∇f(x)−∇f(y)∣∣=∇2f(ξ)≼L⋅I
同样可以达到线性收敛级别的收敛速度。
相关参考:
【优化算法】梯度下降法-总体介绍
相关文章:

机器学习笔记之优化算法(十)梯度下降法铺垫:总体介绍
机器学习笔记之优化算法——梯度下降法铺垫:总体介绍 引言回顾:线搜索方法线搜索方法的方向 P k \mathcal P_k Pk线搜索方法的步长 α k \alpha_k αk 梯度下降方法整体介绍 引言 从本节开始,将介绍梯度下降法 ( Gradient Descent,GD ) …...

Selenium 根据元素文本内容定位
使用xpath定位元素时,有时候担心元素位置会变,可以考虑使用文本内容来定位的方式。 例如图中的【股市】按钮,只有按钮文本没变,即使位置变化也可以定位到该元素。 xpath内容样例: # 文本内容完全匹配 //button[text(…...

第17章-Spring AOP经典应用场景
文章目录 一、日志处理二、事务控制三、参数校验四、自定义注解五、AOP 方法失效问题1. ApplicationContext2. AopContext3. 注入自身 六、附录1. 示例代码 AOP 提供了一种面向切面操作的扩展机制,通常这些操作是与业务无关的,在实际应用中,可…...

Leetcode周赛 | 2023-8-6
2023-8-6 题1体会我的代码 题2我的超时代码题目体会我的代码 题3体会我的代码 题1 体会 这道题完全就是唬人,只要想明白了,只要有两个连续的数的和,大于target,那么一定可以,两边一次切一个就好了。 我的代码 题2 我…...

ts中interface自定义结构约束和对类的约束
一、interface自定义结构约束对后端接口返回数据 // interface自定义结构 一般用于较复杂的结构数据类型限制 如后端返回的接口数据// 首字母大写;用分割号隔开 interface Iobj{a:number;b:string } let obj:Iobj {a:1,b:2 }// 复杂类型 模拟后端返回的接口数据 interface Il…...

Oracle单实例升级补丁
目录 1.当前DB环境2.下载补丁包和opatch的升级包3.检查OPatch的版本4.检查补丁是否冲突5.关闭数据库实例,关闭监听6.应用patch7.加载变化的SQL到数据库8.ORACLE升级补丁查询 oracle19.3升级补丁到19.18 1.当前DB环境 [oraclelocalhost ~]$ cat /etc/redhat-releas…...

力扣初级算法(二分查找)
力扣初级算法(二分法): 每日一算法:二分法查找 学习内容: 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 2.二分查找流程&…...

探索未来:直播实时美颜SDK在增强现实(AR)直播中的前景
在AR直播中,观众可以与虚拟元素实时互动,为用户带来更加丰富、沉浸式的体验。那么,直播美颜SDK在AR中有哪些应用呢?下文小编将于大家一同探讨美颜SDK与AR有哪些关联。 一、AR直播与直播实时美颜SDK的结合 增强现实技术在直播中…...

SQL 单行子查询 、多行子查询、单行函数、聚合函数 IN 、ANY 、SOME 、ALL
单行子查询 子查询结果是 一个列一行记录 select a,b,c from table where a >(select avg(xx) from table ) 还支持这种写法,这种比较少见 select a,b,c from table where (a ,b)(select xx,xxx from table where col‘000’ )…...
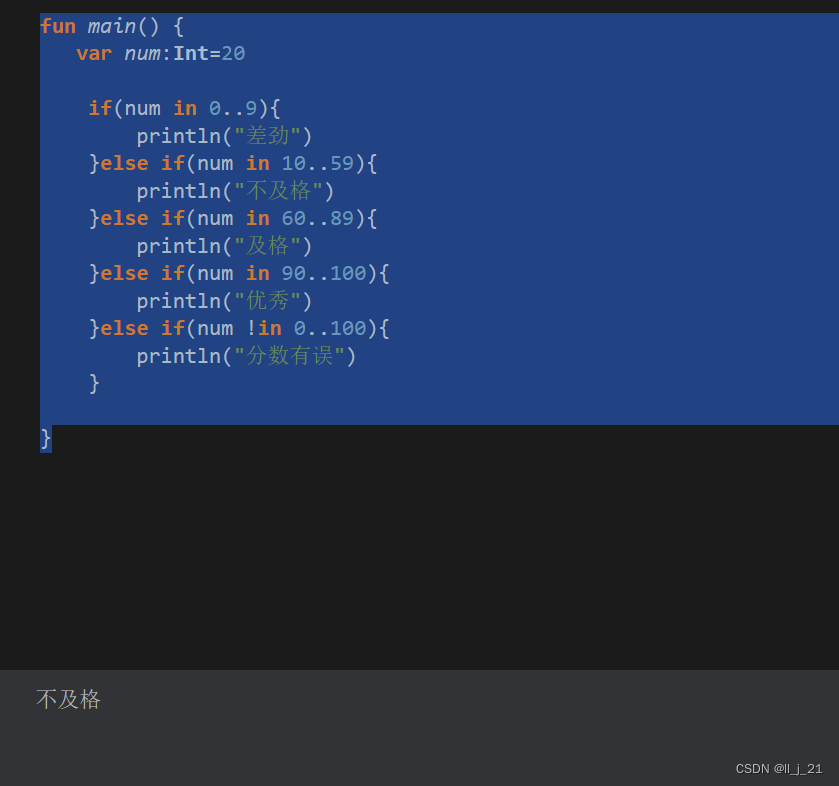
【第一阶段】kotlin的range表达式
range:范围:从哪里到哪里的意思 in:表示在 !in:表示不在 … :表示range表达式 代码示例: fun main() {var num:Int20if(num in 0..9){println("差劲")}else if(num in 10..59){println("不及格")}else if(num in 60..89…...
)
网络防御(5)
一、结合以下问题对当天内容进行总结 1. 什么是恶意软件? 2. 恶意软件有哪些特征? 3. 恶意软件的可分为那几类? 4. 恶意软件的免杀技术有哪些? 5. 反病毒技术有哪些? 6. 反病毒网关的工作原理是什么? 7. 反…...

gradle 命令行单元测试执行问题
文章目录 问题:命令行 执行失败最终解决方案(1)ADB命令(2)Java 环境配置 问题:命令行 执行失败 命令行 执行测试命令 无法使用(之前还能用的。没有任何改动,又不能用了) …...

剑指Offer12.矩阵中的路径 C++
1、题目描述 给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平…...

金鸣识别将无表格线的图片转为excel的几个常用方案
我们知道,金鸣识别要将横竖线齐全的表格图片转为excel非常简单,但要是表格线不齐全甚至没有表格线的图片呢?这就没那么容易了,在识别这类图片时,我们一般会使用以下的一种或多种方法进行处理: 1. 基于布局…...

刚刚更新win11,记事本消失怎么处理?你需要注意些什么?
记录window11的bug hello,我是小索奇 昨天索奇从window10更新到了window11,由于版本不兼容卸载了虚拟机,这是第一个令脑壳大的,算了,还是更新吧,了解了解win11的生态,后期重新装虚拟机 第一个可…...

【QT】 QTabWidgetQTabBar控件样式设计(QSS)
很高兴在雪易的CSDN遇见你 ,给你糖糖 欢迎大家加入雪易社区-CSDN社区云 前言 本文分享QT控件QTabWidget&QTabBar的样式设计,介绍两者可以自定义的内容,以及如何定义,希望对各位小伙伴有所帮助! 感谢各位小伙伴…...

【个人记录】CentOS7 编译安装最新版本Git
说明 使用yum install git安装的git版本是1.8,并不是最新版本,使用gitlab-runner托管时候会拉项目失败,这里使用编译源码方式安装最新版本的git。 基础环境安装 echo "nameserver 8.8.8.8" >> /etc/resolv.conf curl -o /…...

【Linux】计算机网络的背景和协议分层
文章目录 网络发展协议何为协议网络协议协议分层OSI七层模型TCP/IP五层模型(四层) 基本通信流程mac地址和ip地址网络通信本质 网络发展 从一开始计算机作为一台台单机使用,到现在网络飞速发展,从局域网Lan建立起局域网࿰…...

代理模式:静态代理+JDK/CGLIB 动态代理
文章目录 1. 代理模式2. 静态代理3. 动态代理3.1. JDK 动态代理机制3.1.1. 介绍 3.1.2. JDK 动态代理类使用步骤3.1.3. 代码示例3.2. CGLIB 动态代理机制3.2.1. 介绍3.2.2. CGLIB 动态代理类使用步骤3.2.3. 代码示例 3.3. JDK 动态代理和 CGLIB 动态代理对比 4. 静态代理和动态…...

gps虚拟定位 AnyGo for Mac 中文
要在AnyGo中进行Gps位置模拟,您只需连接您的设备并选择“位置模拟”选项,然后输入您想要模拟的位置信息即可。通过使用AnyGo,您可以轻松地模拟任何地方的位置,而无需实际去到那个地方。 借助AnyGo,您可以通过在地图上…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...
