C++——二叉树排序树
文章目录
- 1 二叉搜索树概念
- 2 二叉搜索树操作与模拟实现
- 2.1 二叉搜索树的查找
- 非递归版本
- 递归版本
- 2.2 二叉搜索树的插入
- 非递归版本
- 递归版本
- 2.3 二叉搜索树的删除
- 非递归版本
- 递归版本
- 3 二叉搜索树的应用(K模型、KV模型)
- 4 二叉搜索树的性能分析
1 二叉搜索树概念
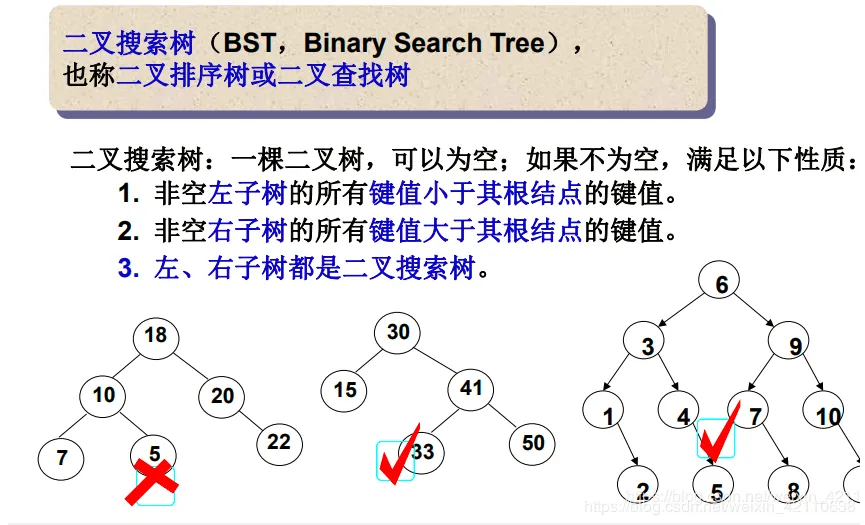
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
- 一般情况下二叉搜索树的数据是不能重复的
2 二叉搜索树操作与模拟实现
完整代码K模型和KV模型代码链接
结点定义:
template<class K>
struct BSTreeNode
{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key):_key(key), _left(nullptr), _right(nullptr){}
};typedef BSTreeNode<K> Node;
2.1 二叉搜索树的查找
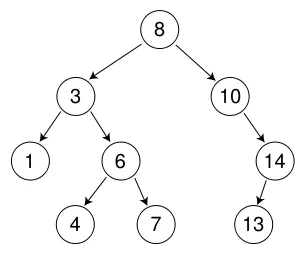
a、从根开始比较,查找,比根大则往右边走查找,比根小则往左边走查找。
b、最多查找高度次,走到到空,还没找到,这个值不存在。
代码实现:
非递归版本
bool Find(const K& key)
{Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return true;}}return false;
}
递归版本
bool _FindR(Node* root, const K& key)
{if (root == nullptr)//没找到return false;if (root->_key < key)//被查找到的值大于当前结点,去右树找return _FindR(root->_right, key);else if (root->_key > key)//被查找到的值小于当前结点,去左树找return _FindR(root->_left, key);else//找到了return true;
}
2.2 二叉搜索树的插入
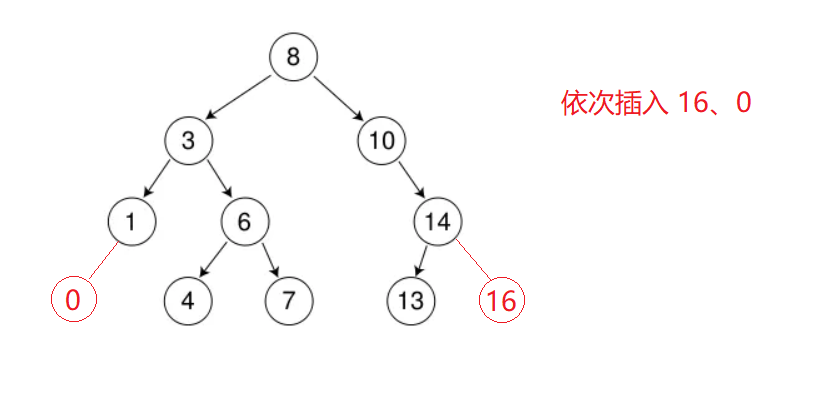
插入的具体过程如下:
a. 树为空,则直接新增节点,给root指针赋值
b. 树不空,按二叉搜索树性质查找插入位置,插入新节点
代码实现:
非递归版本
bool Insert(const K& key)
{if (_root == nullptr){_root = new Node(key);return true;}Node* parent = nullptr;//记录父节点Node* cur = _root;//_root成员变量while (cur)//循环找插入位置{if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{return false;//这里当插入的值已经存在的时候就不能再插入了//默认二叉搜索树不能有重复的值}}//cur此时为nullptr//父节点parent也被记录cur = new Node(key);if (parent->_key < key)//寻找该正确的插入位置{parent->_right = cur;}else{parent->_left = cur;}return true;
}
递归版本
可以考虑再增加一个parent参数。
但下面的方法更加巧妙
下面代码传root的引用两个用处:
1、如果传进来的就是一颗空树,直接给root赋值就可以了,比较容易理解.
2、因为传的是引用,所以root也是上一步递归传入的root->right或者root->_left的别名,非常巧妙的是root = new Node(key);就等价于root->right=new Node(key);或者root->_left=new Node(key);,刚好把结点就赋值到正确的位置,省去了上面非递归方法的还需要记录父节点的步骤。
bool _InsertR(Node*& root, const K& key)//注意细节传的是root的引用
{ if (root == nullptr){root = new Node(key);return true;}if (root->_key < key)//插入的值比当前的结点的值大,就往右树走。return _InsertR(root->_right, key);else if (root->_key > key)//插入的值比当前的结点的值小,就往左树走。return _InsertR(root->_left, key);else//插入的值和当前结点的值相等,不需要插入,返回falsereturn false;
}
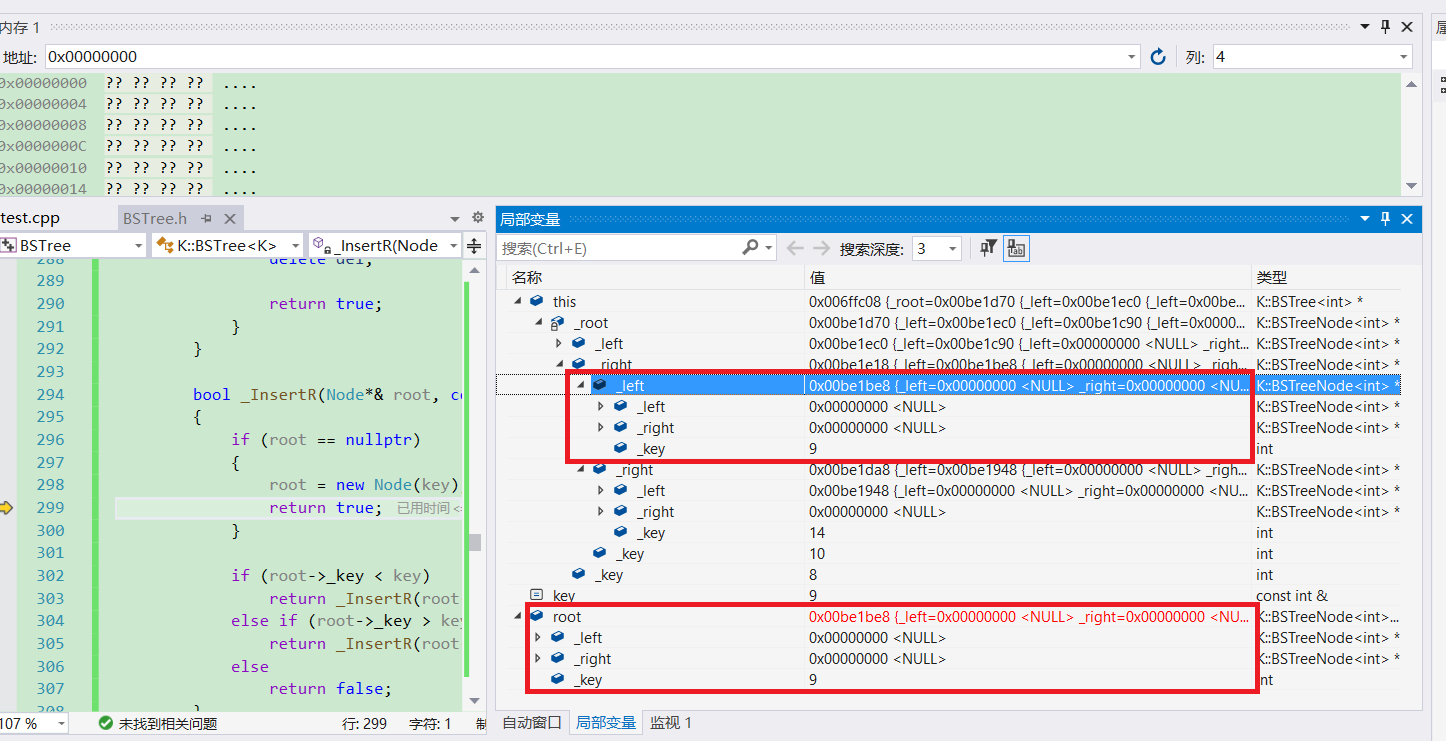
下面是插入9的代码调试,可以发现确实root和上一步root->left的地址是一样的,可见引用在C++中的作用是多么大。
2.3 二叉搜索树的删除
首先查找元素是否在二叉搜索树中,如果不存在,则返回, 否则要删除的结点可能分下面四种情况:
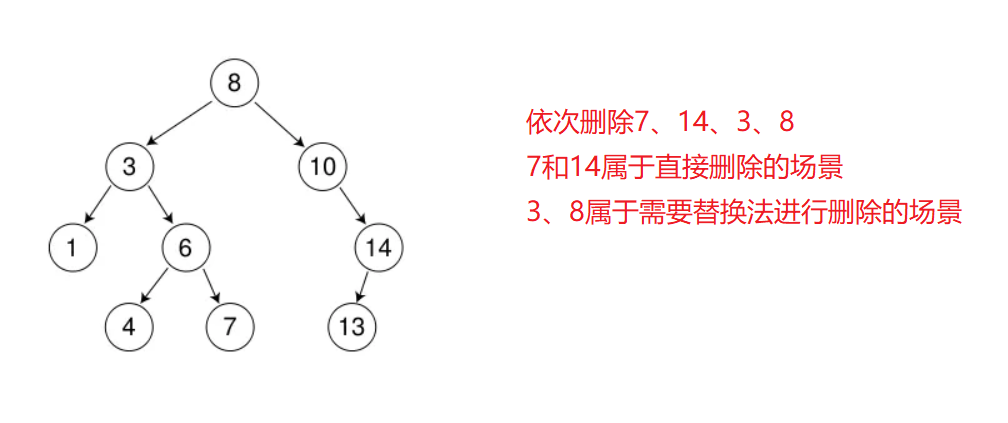
a. 要删除的结点无孩子结点(例如1、4、7、13)
b. 要删除的结点只有左孩子结点(例如14)
c. 要删除的结点只有右孩子结点(例如10)
d. 要删除的结点有左、右孩子结点(例如3、6、8)
看起来删除节点有4种情况,实际情况a可以与情况b或者c合并起来,因此真正的删除过程如下:
- 情况b:删除该结点,并且使该删除节点的双亲结点指向该删除节点的左孩子结点——直接删除(托孤)
- 情况c:删除该结点,并且使该删除节点的双亲结点指向该删除结点的右孩子结点——直接删除(托孤)
- 情况d:
找被删除结点 左子树的最大 或者 右子树的最小 用它的值填补到被删除节点中(这样才能保证二叉排序树的结构不被破坏),再来删除这个 左子树最大 或者 右子树最小结点——替换法删除。
针对情况d,下面图中,想删除8用左子树的最大或者右子树的最小
那么由于二叉排序树特殊的结构其实
左子树的最大 也就是 左子树的最右结点——从上往下遍历,第一个没有右孩子的结点——7
右子树的最小 也就是 右子树的最左结点——从上往下遍历,第一个没有左孩子的结点——10
代码实现:
提前声明:下面非递归和递归版本都用的是右子树的最小结点来进行替换删除的。
具体细节详解在下面代码注释中:一边看图一边看代码注释效果更佳!
非递归版本
bool Erase(const K& key)
{Node* parent = nullptr;//记录父节点Node* cur = _root;//_root成员变量while (cur){//能找到开始删除if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else//被删除目标已经找到,就存在cur里{if (cur->_left == nullptr)//被删除结点的左为空——只有右孩子{//if (parent == nullptr)//如果被删除的就是根节点if (cur == _root)//如果被删除的就是根节点{_root = cur->_right;}else{if (parent->_left == cur)//如果我是父亲结点的左孩子{parent->_left = cur->_right;}else//如果我是父亲结点的右孩子{parent->_right = cur->_right;}}delete cur;}else if (cur->_right == nullptr)//被删除结点右为空——只有左孩子{//if (parent == nullptr)//如果被删除的就是根节点if (cur == _root)//如果被删除的就是根节点{_root = cur->_left;}else{if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;}else//被删除的结点左右子树都不为空,替换删除{// 开始找右子树的最小节点Node* parent = cur; //细节赋值curNode* minRight = cur->_right;while (minRight->_left){parent = minRight;minRight = minRight->_left;}//运行到这里已经找到了右子树最小结点cur->_key = minRight->_key;//直接覆盖被删除结点的值,或者让右子树和被删除结点交换都可以//minRight是右子树的最左结点——一定没有左孩子//而且要特别注意:删除3和删除8结点是不一样的,一定要考虑全面if (minRight == parent->_left)//删除8结点的情况,对于10结点的处理{parent->_left = minRight->_right;}else//删除3结点的情况,对于4结点的处理{parent->_right = minRight->_right;}delete minRight;}return true;}}//找不到需要被删除的节点返回falsereturn false;
}
递归版本
bool _EraseR(Node*& root, const K& key)
{if (root == nullptr)//没有找到 或者 root一开始传入的就是一个空树{return false;}//开始找要被删除的结点并将其删除if (root->_key < key)//要被删除的值比当前的值大就再去右树找{return _EraseR(root->_right, key);}else if (root->_key > key)//要被删除的值比当前的值小就再去左树找{return _EraseR(root->_left, key);}else//找到了!!!开始删除{Node* del = root;//记录当前结点,方便后面delete//被删除结点只有左孩子,例如14if (root->_right == nullptr){root = root->_left;//被赋值的root也是上一层递归root->_right的别名}//被删除结点只有右孩子,例如:10else if (root->_left == nullptr){root = root->_right;//被赋值的root也是上一层递归root->_left的别名}else//被删除结点有两个孩子{Node* minRight = root->_right;//找右子树的最左——最小while (minRight->_left){minRight = minRight->_left;}//让被删除结点跟最小值交换swap(root->_key, minRight->_key);// 交换完右子树还是一颗二叉排序树// 转换成在子树中去删除节点return _EraseR(root->_right, key);}delete del;return true;}
}
完整代码K模型和KV模型代码链接
3 二叉搜索树的应用(K模型、KV模型)
- K模型:K模型即只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到的值。比如:给一个单词word,判断该单词是否拼写正确,具体方式如下:
- 以词库中所有单词集合中的每个单词作为key,构建一棵二叉搜索树
- 在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误。
- KV模型:每一个关键码key,都有与之对应的值Value,即<Key, Value>的键值对。该种方式在现实生活中非常常见:
- 比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文<word, chinese>就构成一种键值对;
- 再比如统计单词次数,统计成功后,给定单词就可快速找到其出现的次数,单词与其出现次数就是<word, count>就构成一种键值对。
4 二叉搜索树的性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数,即结点越深,则比较次数越多。
但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:
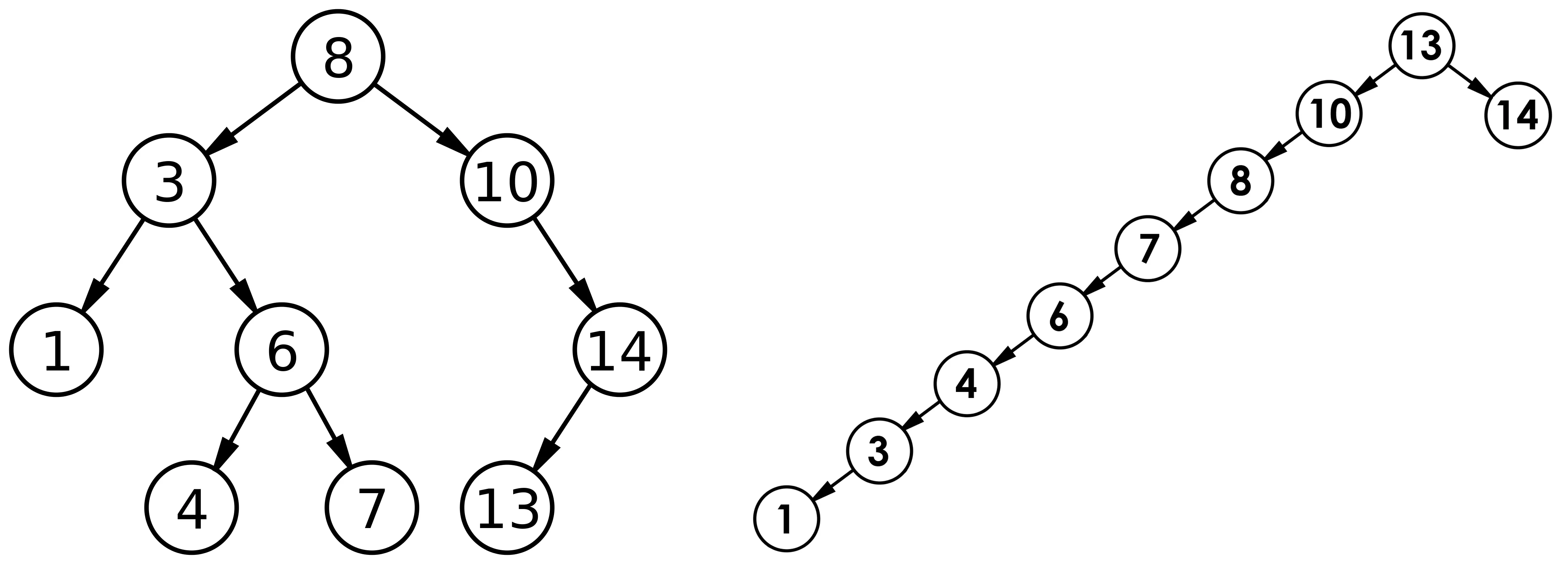
最优情况下,二叉搜索树为完全二叉树(或者接近完全二叉树),其平均比较次数为:log2Nlog_2 Nlog2N。
最差情况下,二叉搜索树退化为单支树(或者类似单支),其平均比较次数为:N{N}N。
相关文章:

C++——二叉树排序树
文章目录1 二叉搜索树概念2 二叉搜索树操作与模拟实现2.1 二叉搜索树的查找非递归版本递归版本2.2 二叉搜索树的插入非递归版本递归版本2.3 二叉搜索树的删除非递归版本递归版本3 二叉搜索树的应用(K模型、KV模型)4 二叉搜索树的性能分析1 二叉搜索树概念…...
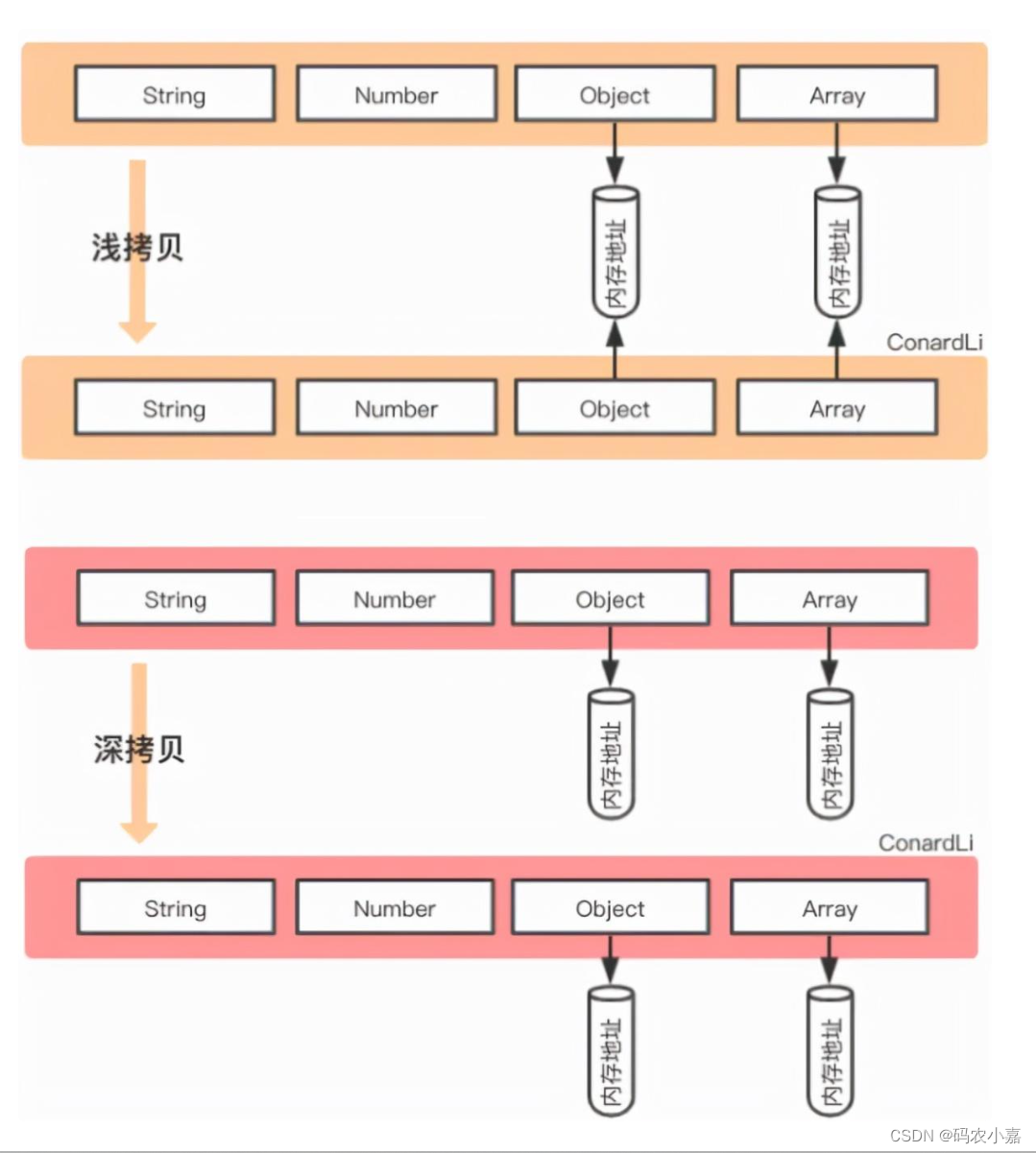
深拷贝浅拷贝的区别?如何实现一个深拷贝?
一、数据类型存储 JavaScript中存在两大数据类型: 基本类型 Number String null Undefined Boolean symbol引用类型 array object function 基本类型数据保存在在栈内存中 引用类型数据保存在堆内存中,引用数据类型的变量是一个指向堆内存中实际对象的…...
Linux应用编程下连接本地数据库进行增删改查系列操作
文章目录前言一、常用SQL操作语句二、相关函数解析三、连接本地数据库四、编译运行五、程序源码前言 本篇为C语言应用编程下连接Linux本地数据库进行增删改查系列操作。 在此之前,首先当然是你需要具备一定的数据库基础,所以下面我先列出部分常用的SQL…...

图论学习03
图神经网络模型介绍 将图神经网络分为基于谱域上的模型和基于空域上的模型,并按照发展顺序详解每个类别中的重要模型。 基于谱域的图神经网络 谱域上的图卷积在图学习迈向深度学习的发展历程上起到了关键性的作用。三个具有代表性的谱域图神经网络 谱图卷积网络切…...

解决qt中cmake单独存放 .ui, .cpp, .h文件
设想 项目文件较多,全部放在一个目录下就像依托答辩。 希望能将头文件放入include,ui文件放入ui,源文件放入src。 为了将Qt代码和一般非Qt代码分离开,进一步地: 将Qt源文件放入qt_src,普通源文件放入sr…...

操作系统(day12)-- 基本分段存储,段页式存储
基本分段存储管理方式 不会产生内部碎片,会产生外部碎片 分段 按照程序自身的逻辑关系划分为 若干个段,每个段都有一个段名,每段从0开始编址 分段存储管理方式中一个段表项由段号(隐含)、段长、基地址 分段的段表项固…...

疯狂弹出请插入多卷集的最后一张磁盘窗口
整个人嘛了,今天插上U盘,跟tmd中了病毒一样, 屏幕疯狂弹出窗口, 提示请插入多卷集的最后一张磁盘! 点确定之后他继续弹出,点取消它也继续弹出, 关掉一个又弹出来一个,妈的&#x…...
Spark12: SparkSQL入门
一、SparkSQL Spark SQL和我们之前讲Hive的时候说的hive on spark是不一样的。hive on spark是表示把底层的mapreduce引擎替换为spark引擎。而Spark SQL是Spark自己实现的一套SQL处理引擎。Spark SQL是Spark中的一个模块,主要用于进行结构化数据的处理。它提供的最核…...

show profile和trance分析SQL
目录 一.show profile分析SQL 二.trance分析优化器执行计划 一.show profile分析SQL Mysql从5.0.37版本开始增加了对show profiles和show profile语句的支持。show profiles能够在做SQL优化时帮助我们了解时间都耗费到哪里去了。。 通过have_profiling参数,能够…...
[AI生成图片] 效果最好的Midjourney 的介绍和使用
Midjourney介绍: 是一个文本生成图片的扩散模型,能够根据输入的任何文本生成令人难以置信的图像,让数十亿人在几秒钟内创造惊人的艺术。为方便用户控制和快速生成图片,打开后在页面底部输入文本内容,稍等一小会&#…...
 的核心原理)
Vue.use( ) 的核心原理
首先来思考几个问题: Vue.use是什么? vue.use() 是vue提供的一个静态方法,主要是为了注册插件,增加vue的功能。 Vue.use( plugin ) plugin只能是Object 或 Function vue.use()做了什么工作? 该js如果是对象 该对象…...
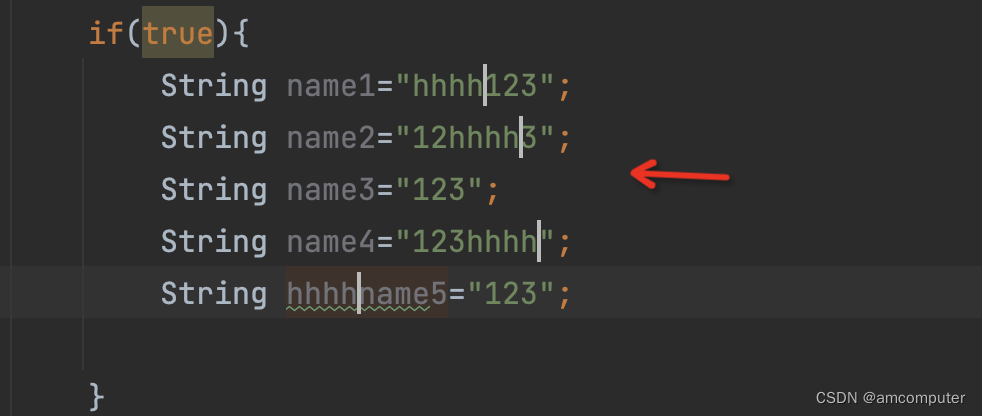
idea同时编辑多行-winmac都支持
1背景介绍 idea编辑器非常强大,其中一个功能非常优秀,很多程序员也非常喜欢用。这个功能能够大大大提高工作效率-------------多行代码同时编辑 2win 2.1方法1 按住alt鼠标左键上/下拖动即可 这样选中多行后,可以直接多行编辑。 优点&a…...

亿级高并发电商项目-- 实战篇 --万达商城项目 十一(编写商品搜索功能、操作商品同步到ES、安装RabbitMQ与Erlang,配置监听队列与消息队列)
👏作者简介:大家好,我是小童,Java开发工程师,CSDN博客博主,Java领域新星创作者 📕系列专栏:前端、Java、Java中间件大全、微信小程序、微信支付、若依框架、Spring全家桶 Ǵ…...

数据结构概述和稀疏数组
数据结构和算法内容介绍 1)算法是程序的灵魂,优秀的程序可以在海量数据计算时,仍然保持高速计算 数据结构和算法概述 1)程序 数据结构算法 2)学好数据结构可以编写出更加漂亮,更加有效率的代码 3&…...
宝塔搭建实战人才求职管理系统adminm前端vue源码(三)
大家好啊,我是测评君,欢迎来到web测评。 上一期给大家分享骑士cms后台admin前端vue在本地运行打包、宝塔发布部署的方式,本期给大家分享,后台adminm移动端后台vue前端怎么在本地运行,打包,实现线上功能更新…...

服务器是干什么用的?
首先,什么是服务器?服务器是提供计算服务器和网络服务的设备。服务器和计算机由CPU、硬盘、内存、系统总线等组成。比如我们访问一个网站,点击这个网站会发出访问请求,服务器会响应服务请求,进行相应的处理,…...

C++ 之结构体与共用体
文章目录参考描述结构体使用(基本)声明初始化先创建后初始化C 11 列表初始化使用(进阶)结构数组声明(拓展)声明及创建声明及初始化匿名结构体细节外部声明与内部声明成员赋值共用体存储空间匿名共用体同化尾…...
)
Java基础知识汇总(良心总结)
1. 前言 本文章是对Java基础知识进行了汇总,方便大家学习。 申明:文章的内容均来自黑马程序员,博主只是将其搬到了CSDN上以共享给大家学习 2. 目录 Day01 Java学习笔记之《开章》 Day02 Java学习笔记之《运算符》 Day03 Java学习笔记之《流程…...
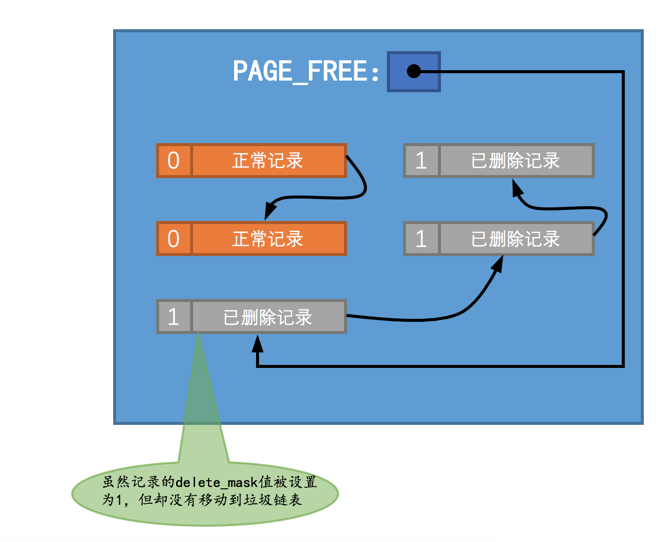
InnoDB之Undo log格式
1. 前言 InnoDB有两大日志模块,分别是redo log和undo log。为了避免磁盘随机写,InnoDB设计了redo log,数据写入时只写缓冲页和redo log,脏页由后台线程异步刷盘,哪怕系统崩溃也能根据redo log恢复数据。但是我们漏了一…...

一问学习StreamAPI终端操作
Java Stream管道流是用于简化集合类元素处理的java API。 在使用的过程中分为三个阶段: 将集合、数组、或行文本文件转换为java Stream管道流管道流式数据处理操作,处理管道中的每一个元素。上一个管道中的输出元素作为下一个管道的输入元素。管道流结果…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...
