算法的时间复杂度
算法在编写成可执行程序后,运行时需要消耗时间资源和空间(内存)资源,因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的。
时间复杂度主要衡量一个算法运行的快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间,今天我们主要来讲讲时间复杂度。
目录
一、时间复杂度的概念
二、大O的渐进表示法
三、常见的时间复杂度计算
一、时间复杂度的概念
一个算法所花的时间与其中语句的执行次数成正比,算法中的基本操作的执行次数,为算法的时间复杂度。
二、大O的渐进表示法
实际计算时间复杂度时,我们并不需要计算精确的执行次数,而只需要大概执行次数,那么这里我们使用大O的渐进表示法。
大O符号:是用于描述函数渐进行为的数学符号。
推导大O阶的方法:
1、用常数1取代运行时间中所有的加法常数。
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高阶项存在且不是1,则去除与这个项相乘的常数,得到的结果就是大O阶。
另外,有些算法的时间复杂度存在最好、平均、最坏的情况。
最坏情况:
任意输入规模的最大运行次数(上线)
平均情况:
任意输入规模的期望运行次数
最好情况:
任意输入规模的最小运行次数
例如,在一个长度为N的数组中搜索一个数据x
最好情况:一次找到
平均情况:N/2次找到
最坏情况:N次找到
在实际中一般情况关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)
三、常见的时间复杂度计算
实例1:
void BubbleSort(int *a,int n)
{assert(a);for(size_t end=n;end>0;--end){int exchange = 0;for(size_t i=1;i<end;++i){if(a[i-1]>a[i]){Swap(&a[i-1],&a[i]);exchange=1;}}if(exchange=0)break;}
}
该例子为冒泡排序,最好的情况为,比较完一轮(N-1次)后,发现就顺序的,所以最好是N次。
最坏是(N*(N+1))/2次,通过推导大O阶方法+时间复杂度一般看最坏,时间复杂度为O(N^2).
实例2:
//二分查找
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n - 1;while (begin <= end){int mid = begin + ((end - begin) >> 1);if (a[mid] < x){begin = mid + 1;}else if(a[mid]>x){end = mid - 1;}else{return mid;}}return -1;
}二分查找:
最好情况:中间那个数就是要找的O(1)
最坏情况:一直除2,,到只剩一个值时,要么找到了,要么找不到。
假设N是数组个数,x是最坏查找次数,N/2/2/2……/2=1
2^x=N,x=logN(logN在算法分析中表示以2为底数,N为对数,有些地方也写成lg N)
实例3:
//计算斐波那契数列的时间复杂度
long long Fib(size_t N)
{if (N < 3)return 1;return Fib(N - 1) + Fib(N - 2);
}
运用等比数列求和公式可知,执行次数为2^N的数量级
所以时间复杂度应为O(2^N)
实例4:
//计算阶乘递归Fac的时间复杂度
long long Fac(size_t N)
{if (0 == N)return 1;return Fac(N - 1) * N;
}时间复杂度为O(N)
相关文章:

算法的时间复杂度
算法在编写成可执行程序后,运行时需要消耗时间资源和空间(内存)资源,因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的。 时间复杂度主要衡量一个算法运行的快慢,而空间复杂度主要衡量一个算法运…...
 | 机试题算法思路 【2023】)
华为OD机试 - 叠放书籍(Python) | 机试题算法思路 【2023】
最近更新的博客 华为OD机试 - 寻找路径 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - 五键键盘 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - IPv4 地址转换成整数 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - 对称美学 | 备考思路,刷题要点,答疑 …...
进程间通信(重点)
概念 进程是一个独立的资源分配单元,不同进程之间的资源是独立的进程并非孤立的,不同进程需要进行信息的交互和状态的传递,因此需要进程之间的通信【IPC: Inter processes communication】 如qq聊天,qq在每个人的手机上是独立的…...
Reverse入门[不断记录]
文章目录前言一、[SWPUCTF 2021 新生赛]re1二、[SWPUCTF 2021 新生赛]re2三、[GFCTF 2021]wordy[花指令]四、[NSSRound#3 Team]jump_by_jump[花指令]五、[NSSRound#3 Team]jump_by_jump_revenge[花指令]前言 心血来潮,想接触点Reverse,感受下Reverse&am…...
如何实现外网访问内网ip?公网端口映射或内网映射来解决
本地搭建服务器应用,在局域网内可以访问,但在外网不能访问。如何实现外网访问内网ip?主要有两种方案:路由器端口映射和快解析内网映射。根据自己本地网络环境,结合是否有公网IP,是否有路由权限,…...

[acwing周赛复盘] 第 91 场周赛20230218
[acwing周赛复盘] 第 91 场周赛20230218 一、本周周赛总结二、 4861. 构造数列1. 题目描述2. 思路分析3. 代码实现三、4862. 浇花1. 题目描述2. 思路分析3. 代码实现四、4863. 构造新矩阵1. 题目描述2. 思路分析3. 代码实现六、参考链接一、本周周赛总结 这周挺难的。T1 贪心分…...

蓝桥12届
小蓝准备用 256MB 的内存空间开一个数组,数组的每个元素都是 32 位 二进制整数,如果不考虑程序占用的空间和维护内存需要的辅助空间,请问 256MB 的空间可以存储多少个 32 位二进制整数?1MB 1024KB 1KB 1024字节(byte) 1字节 8位…...
)
华为OD机试 - 斗地主(JS)
斗地主 题目 斗地主起源于湖北十堰房县, 据传是一位叫吴修全的年轻人根据当地流行的扑克玩法“跑得快”改编的, 如今已风靡整个中国,并流行于互联网上 牌型: 单顺,又称顺子,最少5张牌,最多12张牌(3...A),不能有2, 也不能有大小王,不计花色 例如:3-4-5-7-8,7-8-9-1…...

【MyBatis】| MyBatis的注解式开发
目录 一:MyBatis的注解式开发 1. Insert注解 2. Delete注解 3. Update注解 4. Select注解 5. Results注解 一:MyBatis的注解式开发 MyBatis中也提供了注解式开发⽅式,采⽤注解可以减少Sql映射⽂件的配置。 当然,使⽤注…...
python自制PDF转换.PNG格式图片(按每页生成图片完整源码)小工具!
使用PyQt5应用程序制作PDF转换成图片的小工具,可以导入PDF文档后一键生成对应的PNG图片。 PDF图片转换小工具使用的中间件: python版本:3.6.8 UI应用版本:PyQt5 PDF文件操作非标准库:PyPDF2 PNG图片生成库࿱…...

Go 数组和切片反思
切片的底层数据结构是数组,所以,切片是基于数组的上层封装,使用数组的场景,也完全可以使用切片。 类型比较 我看到 go 1.17 有对切片和数组转换的优化,禁不住纳闷,有什么场景是必须数组来完成的呢&#x…...
win10电脑性能优化设置
win10电脑性能优化设置 目录win10电脑性能优化设置1.桌面图标显示2.wini2.1 “系统”2.1.1专注助手 关2.1.2 电源和睡眠 设置为从不2.1.3 存储 开2.2 网络和Internet2.3 个性化2.4 应用2.5 账户2.6 游戏2.7 隐私墨迹书写和键入个性化:关活动历史记录:全部…...

作为初学者必须要了解的几种常用数据库!
现在已经存在了很多优秀的商业数据库,如甲骨文(Oracle)公司的 Oracle 数据库、IBM 公司的 DB2 数据库、微软公司的 SQL Server 数据库和 Access 数据库。同时,还有很多优秀的开源数据库,如 MySQL 数据库,Po…...

小红书日常实习一面面经
时间:2月13下午 平台:赛码网,视频面大概70分钟顺序大致是下面,讲到哪问到哪,基础知识最好要结合项目或者实际回答,没录音不完全,有错误请指正首先面试官人超级好,细心提问,耐心解答问…...
)
将Nginx 核心知识点扒了个底朝天(一)
什么是Nginx? Nginx是一个 轻量级/高性能的反向代理Web服务器,用于 HTTP、HTTPS、SMTP、POP3 和 IMAP 协议。他实现非常高效的反向代理、负载平衡,他可以处理2-3万并发连接数,官方监测能支持5万并发,现在中国使用ngin…...

SSM项目搭建保姆级教程
文章目录1、什么是SSM框架1.1、持久层1.2、业务层1.3、表现层1.4、View层1.5、SpringMVC执行流程1.6、MyBatis2、SSM实战搭建2.1、创建工程2.2、添加依赖2.3、配置spring.xml文件2.4、配置web.xml文件2.5、log4j.properties2.6、准备表2.7、实体类2.8、mapper2.9、service2.10、…...

LeetCode 350. 两个数组的交集 II
原题链接 难度:easy\color{Green}{easy}easy 题目描述 给你两个整数数组 nums1nums1nums1 和 nums2nums2nums2 ,请你以数组形式返回两数组的交集。返回结果中每个元素出现的次数,应与元素在两个数组中都出现的次数一致(如果出现…...

Python可以解码吗,解码打码是如何实现的
前言 咳咳,进来的铁汁都是抱着学习的心态进来看的吧,咱今天不讲解解码,咱来说说python如何来实现打码功能~ 这一个个进来的 都是标题党吧哈哈哈 有兴趣的可以继续看看哦 最近重温了一档综艺节目 至于叫什么 这里就不细说了 老是看着看着就…...
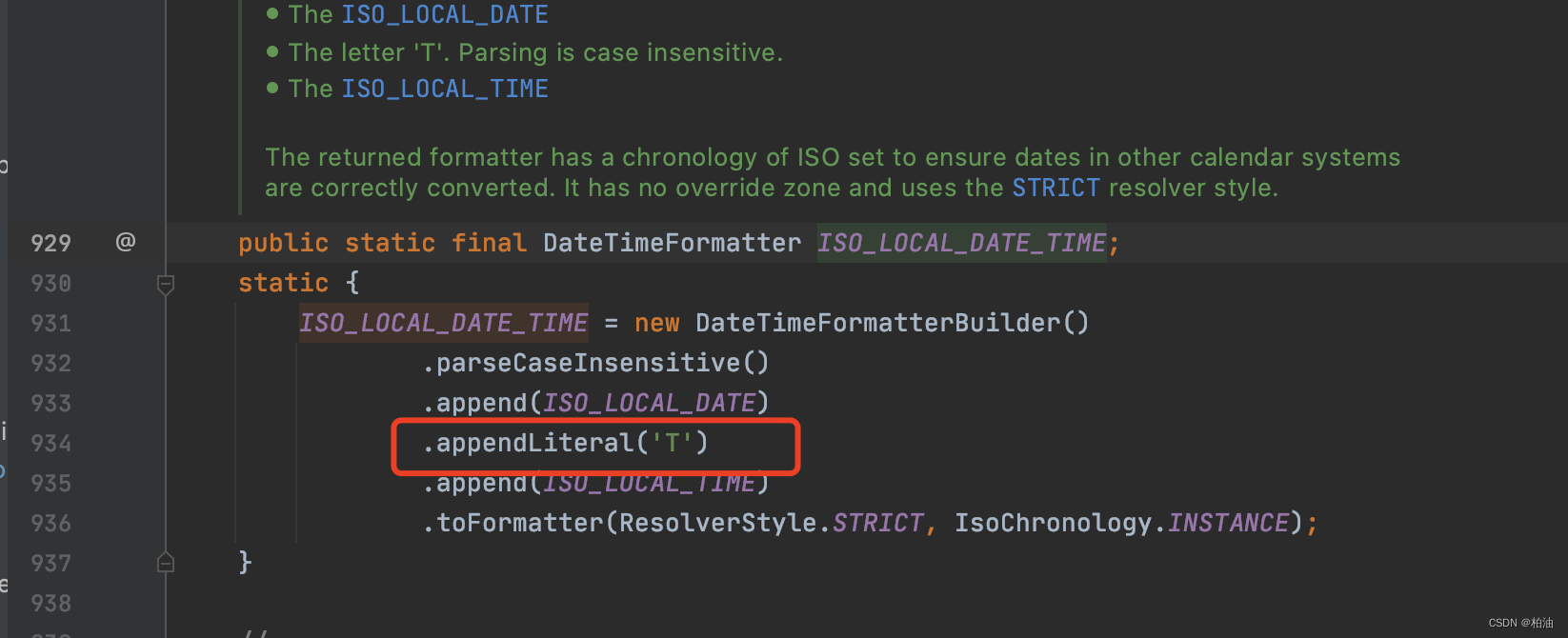
Jackson 序列化:Cannot deserialize value of type `java.time.LocalDateTime`
问题描述 使用 jackson 反序列化异常如下: Caused by: com.fasterxml.jackson.databind.exc.InvalidFormatException: Cannot deserialize value of type java.time.LocalDateTime from String “2023-02-13 19:43:01”: Failed to deserialize java.time.LocalDat…...
_习题)
机试_3_数据结构(一)_习题
数据结构(一)——练习题 学习完第三章-数据结构(一)之后,当然要做相应地练习啦~ 注:上述习题都可以在牛客进行测试。 例如,第2题链接:计算表达式_牛客题霸_牛客网 (nowcoder.com)…...

SGP.22 eSIM通信原理-打电话
三个关键阶段:准备阶段(下载Profile)、激活阶段(网络注册)和使用阶段(拨打电话)。 第一阶段:准备——将中国移动的“身份”下载到手机 用户买了一部支持eSIM的新手机,决定…...

解密Authority核心组件:Authorizer类如何掌控Rails应用权限
解密Authority核心组件:Authorizer类如何掌控Rails应用权限 【免费下载链接】authority *CURRENTLY UNMAINTAINED*. Authority helps you authorize actions in your Rails app. Its ORM-neutral and has very little fancy syntax; just group your models under o…...

Xorbits核心技术解密:自动算子分块如何实现分布式计算革命
Xorbits核心技术解密:自动算子分块如何实现分布式计算革命 【免费下载链接】xorbits Scalable Python DS & ML, in an API compatible & lightning fast way. 项目地址: https://gitcode.com/gh_mirrors/xo/xorbits Xorbits作为一款高性能分布式计算…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...
