VS2017+OpenCV4.5.5 决策树-评估是否发放贷款
决策树是一种非参数的监督学习方法,主要用于分类和回归。
决策树结构
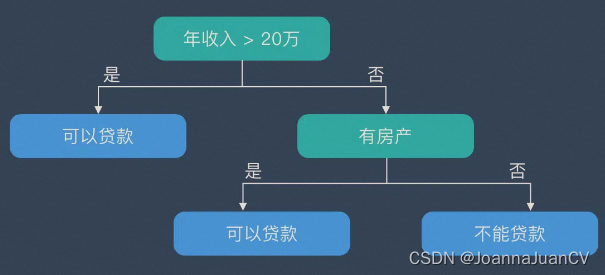
决策树在逻辑上以树的形式存在,包含根节点、内部结点和叶节点。
- 根节点:包含数据集中的所有数据的集合
- 内部节点:每个内部节点为一个判断条件,并且包含数据集中满足从根节点到该节点所有条件的数据的集合。根据内部结点的判断条件测试结果,内部节点对应的数据的集合别分到两个或多个子节点中。
- 叶节点:叶节点为最终的类别,被包含在该叶节点的数据属于该类别。
决策树学习的 3 个步骤
特征选择
在构建决策树的过程中,选择最佳(既能够快速分类,又能使决策树的深度最小)的分叉特征属性是关键所在。这种“最佳性”可以用非纯度进行衡量。如果一个数据集合中只有一种分类结果,则该集合最纯,即一致性好;反之,有许多分类,则不纯,即一致性不好。
一般的原则是,希望通过不断划分节点,使得一个分支节点包含的数据尽可能的属于同一个类别,即“纯度“越来越高。
常用的准则有:熵,基尼指数和分类误差, 公式分别为:
Entropy=E(D)=−∑j=1Jpjlog2pjEntropy = E(D) = -\sum_{j=1}^Jp_j\log_2p_jEntropy=E(D)=−j=1∑Jpjlog2pj
GiniIndex=Gini(D)=∑j=1Jpj(1−pj)=∑j=1Jpj−∑j=1Jpj2=1−∑j=1Jpj2Gini Index = Gini(D) = \sum_{j=1}^Jp_j(1-p_j) = \sum_{j=1}^Jp_j - \sum_{j=1}^Jp_j^2 = 1 - \sum_{j=1}^Jp_j^2GiniIndex=Gini(D)=j=1∑Jpj(1−pj)=j=1∑Jpj−j=1∑Jpj2=1−j=1∑Jpj2
ClassificationErroe=1−max{pj}Classification Erroe = 1- \max{\{p_j\}} ClassificationErroe=1−max{pj}
上述,所有公式中,值越大表示越不纯;式中,DDD表示样本数据的分类及和。设该集合共有JJJ中分类,pjp_jpj表示第jjj种分类的样本率:
pj=NjNp_j = \frac{N_j}{N}pj=NNj
式中,NNN和NjN_jNj分辨表示集合DDD中样本数据的总数和第jjj个分类的样本数量。
决策树生成
选择好特征后,就从根节点触发,对节点计算所有特征的信息增益,选择信息增益最大的特征作为节点特征,根据该特征的不同取值建立子节点;对每个子节点使用相同的方式生成新的子节点,直到信息增益很小或者没有特征可以选择为止。
决策树剪枝
剪枝的主要目的是对抗「过拟合」,通过主动去掉部分分支来降低过拟合的风险。
决策树算法
ID3 算法
ID3 是最早提出的决策树算法,他就是利用信息增益来选择特征的。
C4.5 算法
他是 ID3 的改进版,他不是直接使用信息增益,而是引入“信息增益比”指标作为特征的选择依据。
CART(Classification and Regression Tree)
这种算法即可以用于分类,也可以用于回归问题。CART 算法使用了基尼系数取代了信息熵模型。
测试用例-评估是否发放贷款
#include<iostream>
#include<opencv2/highgui/highgui.hpp>
#include<opencv2/core/core.hpp>
#include<opencv2/imgproc/imgproc.hpp>
#include<opencv2/ml/ml.hpp>using namespace std;
using namespace cv;
using namespace cv::ml;static const char* var_desc[] =
{"Age (young=Y, middle=M, old=O)","Salary? (Low=L, medium=M, high=H)","Own_House? (false=N, true=Y)","Own_Car? (false=N, true=Y)","Credit_Rating (fair=F, good=G, excellent=E",0
};int main(int argc, char *argv[])
{//训练样本:年龄,薪水,房子,车,信贷情况float trainData[19][5] = { {'Y','L','N','N','F'},{'Y','L','Y','N','G'},{'Y','M','Y','N','G'},{'Y','M','Y','Y','G'},{'Y','H','Y','Y','G'},{'Y','M','N','Y','G'},{'M','L','Y','Y','E'},{'M','H','Y','Y','G'},{'M','L','N','Y','G'},{'M','M','Y','Y','F'},{'M','H','Y','Y','E'},{'M','L','N','N','G'},{'O','L','N','N','G'},{'O','L','Y','Y','E'},{'O','L','Y','N','E'},{'O','M','N','Y','G'},{'O','L','N','N','E'},{'O','H','N','Y','F'},{'O','H','Y','Y','E'},};Mat trainDataMat(19, 5, CV_32FC1, trainData);//cout << trainDataMat << endl;//训练样本的响应值,1代表G -1代表B float labels[19] = { 'N' ,'N' ,'Y','Y','Y','N','Y','Y','N' ,'N','Y','N' ,'N' ,'Y','Y','N' ,'N' ,'N' ,'Y' };Mat labelsMat(19, 1, CV_32FC1, labels);//cout << labelsMat << endl;//建立模型Ptr<DTrees> model = DTrees::create();//树的最大可能深度model->setMaxDepth(8);//节点最小样本数量model->setMinSampleCount(2);//是否建立替代分裂点model->setUseSurrogates(false);//交叉验证次数model->setCVFolds(0);//是否严格修剪model->setUse1SERule(false);//分支是否完全移除model->setTruncatePrunedTree(false);//创建TrainData并进行训练Ptr<TrainData> tData = TrainData::create(trainDataMat, ROW_SAMPLE, labelsMat);model->train(tData);//保存决策树为xml文件const std::string save_file{ "decision_tree_model.xml" }; // .xml, .yaml, .jsonsmodel->save(save_file);float myData[5] = { 'M','H','Y','N','F'};//测试样本Mat myDataMat(5, 1, CV_32FC1, myData);//利用训练好的分类器进行测试样本预测cv::Mat rMat;double r = model->predict(myDataMat, rMat, false);std::cout << "result: " << (char)r <<endl;//测试加载保存的决策树进行预测Ptr<DTrees> dtree = DTrees::load("decision_tree_model.xml");r = dtree->predict(myDataMat, rMat, false);std::cout << "result: " << (char)r << endl;return 0;
}
结果:
result: N
result: N
相关文章:

VS2017+OpenCV4.5.5 决策树-评估是否发放贷款
决策树是一种非参数的监督学习方法,主要用于分类和回归。 决策树结构 决策树在逻辑上以树的形式存在,包含根节点、内部结点和叶节点。 根节点:包含数据集中的所有数据的集合内部节点:每个内部节点为一个判断条件,并且…...

Prometheus 记录规则和警报规则
前提环境: Docker环境 涉及参考文档: Prometheus 录制规则Prometheus 警报规则 语法检查规则 promtool check rules /path/to/example.rules.yml一:录制规则语法 groups 语法: groups:[ - <rule_group> ]rule_group…...

(API)接口测试的关键技术
接口测试也就是API测试,从名字上可以知道是面向接口的测试活动。所以在讲API测试之前,我们应该说清楚接口是什么,那么接口就是有特定输入和特定输出的一套逻辑处理单元,而对于接口调用方来说,不用知道自身的内部实现逻…...

快速排序算法原理 Quicksort —— 图解(精讲) JAVA
快速排序是 Java 中 sort 函数主要的排序方法,所以今天要对快速排序法这种重要算法的详细原理进行分析。 思路:首先快速排序之所以高效一部分原因是利用了离散数学中的传递性。 例如 1 < 2 且 2 < 3 所以可以推出 1 < 3。在快速排序的过程中巧…...

linux环境搭建私有gitlab仓库
搭建之前,需要安装相应的依赖包,并且要启动sshd服务(1).安装policycoreutils-python openssh-server openssh-clients [rootVM-0-2-centos ~]# sudo yum install -y curl policycoreutils-python openssh-server openssh-clients [rootVM-0-2-centos ~]…...

SpringSecurity授权
文章目录工具类使用自定义失败处理代码配置跨域其他权限授权hasAnyAuthority自定义权限校验方法基于配置的权限控制工具类 import javax.servlet.http.HttpServletResponse; import java.io.IOException;public class WebUtils {/*** 将字符串渲染到客户端** param response 渲…...

学习 Python 之 Pygame 开发坦克大战(一)
学习 Python 之 Pygame 开发坦克大战(一)Pygame什么是Pygame?初识pygame1. 使用pygame创建窗口2. 设置窗口背景颜色3. 获取窗口中的事件4. 在窗口中展示图片(1). pygame中的直角坐标系(2). 展示图片(3). 给部分区域设置颜色5. 在窗口中显示文字6. 播放音…...

2.5|iot冯|方元-嵌入式linux系统开发入门|2.13+2.18
一、 Linux 指令操作题(共5题(共 20 分,每小题 4分)与系统工作、系统状态、工作目录、文件、目录、打包压缩与搜索等主题相关。1.文件1.1文件属性1.2文件类型属性字段的第1个字符表示文件类型,后9个字符中,…...
)
一起Talk Android吧(第四百九十六回:自定义View实例二:环形进度条)
文章目录 知识回顾实现思路实现方法示例代码各位看官们大家好,上一回中咱们说的例子是"如何使用Java版MQTT客户端",这一回中咱们说的例子是"自定义View实例二:环形进度条"。闲话休提,言归正转,让我们一起Talk Android吧! 知识回顾 看官们,我们又回…...

上传图片尺寸校验
使用方法 ● Image ● URL ● onload代码: async validImageSize(file, imgWidth, imgHeight) {const img new Image()img.src URL.createObjectURL(file)const { w, h } await new Promise((resolve, reject) > {img.onload () > {const { width: w, he…...
)
【Python】缺失值处理和拉格朗日插值法(含源代码实现)
目录:缺失值处理和拉格朗日插值法一、前言二、理论知识三、代码实现一、前言 对于含有缺失值的数据集,如果通过删除小部分记录达到既定的目标,那么删除含有缺失值的记录的方法是最有效的。然而,这种方法也有很多问题,…...
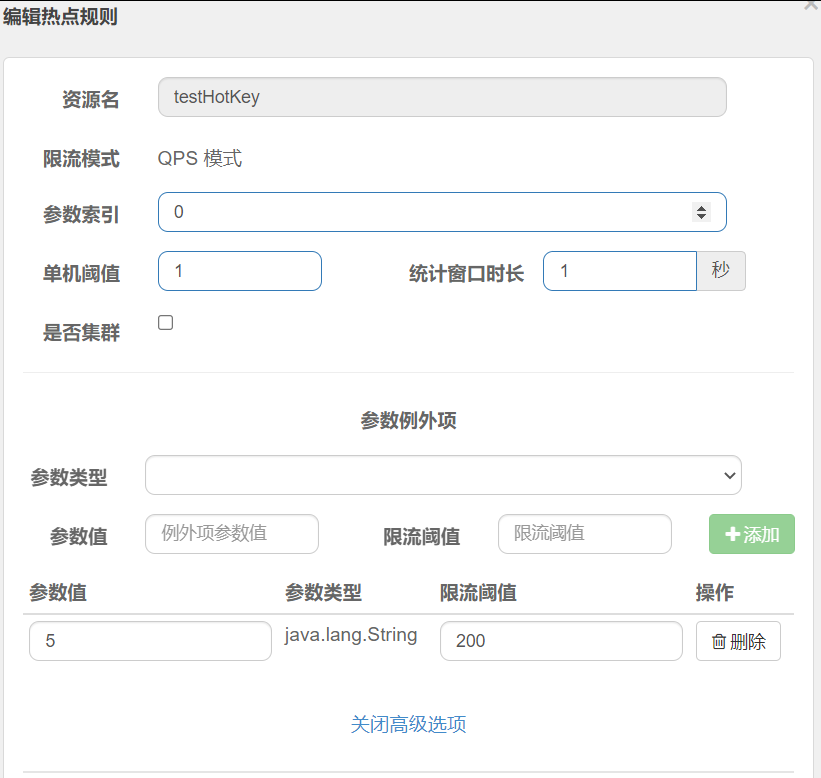
SpringCloudAlibaba-Sentinel
一、介绍官网:https://github.com/alibaba/Sentinel/下载jar包,启动,访问http://localhost:8080/创建module添加如下依赖<!--SpringCloud ailibaba sentinel --><dependency><groupId>com.alibaba.cloud</groupId><artifactId>spring…...

【程序化天空盒】过程记录02:云扰动 边缘光 消散效果
写在前面 写在前面唉,最近筋疲力竭,课题组的东西一堆没做,才刚刚开始带着思考准备练习作品,从去年5月份开始到现在真得学了快一年了,转行学其他的真的好累,,不过还是加油! 下面是做…...
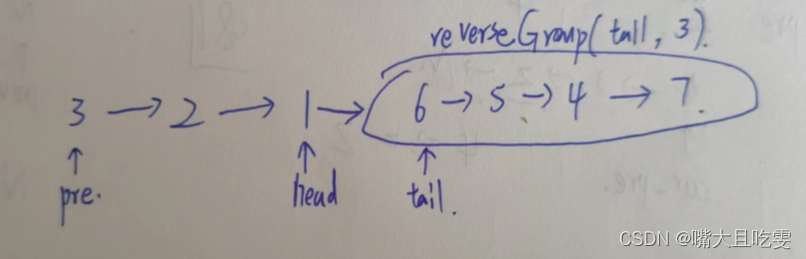
链表OJ(三) 反转链表合集
目录 反转链表 反转链表 II 链表中的节点每k个一组翻转 描述 给定一个单链表的头结点pHead(该头节点是有值的,比如在下图,它的val是1),长度为n,反转该链表后,返回新链表的表头。 数据范围: 0≤n≤10000≤…...
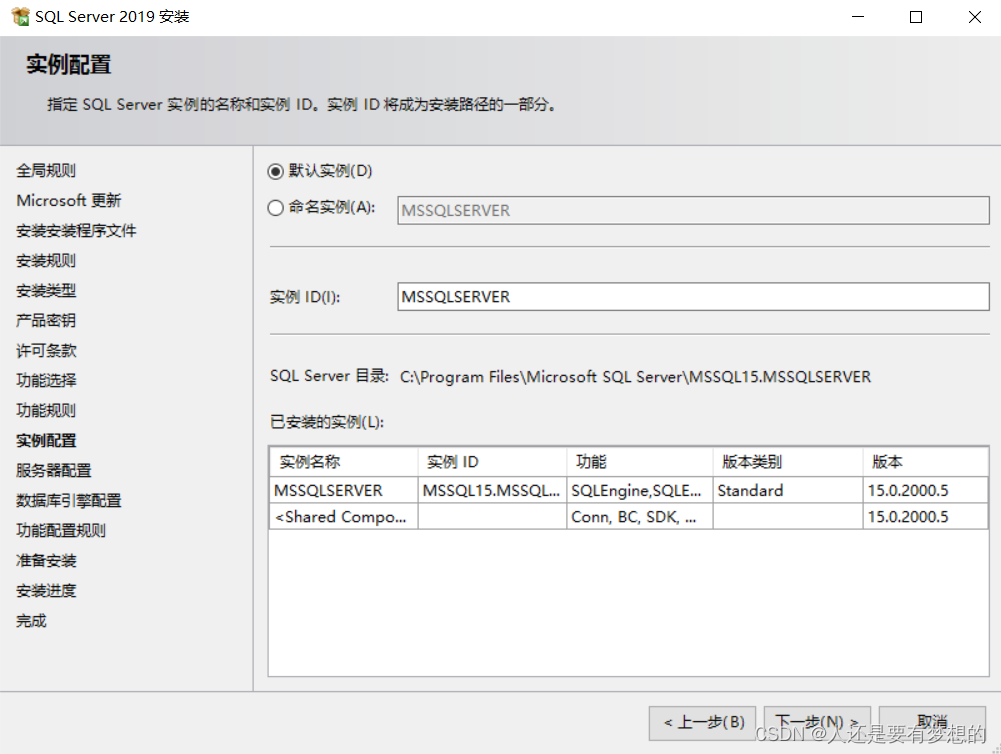
SQLSERVER2019安装步骤过程
第一步官网下载SQLSERVER软件包 目前官网只能下载最新版本2022版本。 通过迅雷下载网址 SQL Server 2019 Enterprise (x64) - DVD (Chinese-Simplified)企业版 ed2k://|file|cn_sql_server_2019_enterprise_x64_dvd_2bfe815a.iso|1632086016|58C258FF0F1D006DD3C1F5F17AF3E…...

Java模块化概述
3 模块化 3.1 模块化概述 Java语言随着这些年的发展已经成为了一]影响深远的编程语言,无数平台,系统都采用Java语言编写。但是,伴随着发展,Java也越来越庞大,逐渐发展成为-门“臃肿” 的语言。而且,无论是运行个大型的…...
)
Connext DDSPersistence Service持久性服务(2)
可选数据库组件及兼容性当Persistence Service配置为PERSISTENT模式时,您可以选择将主题数据存储在文件中还是存储在外部关系数据库中。 唯一支持的外部数据库是MySQL。 当PersistenceService在PERSISTENT模式下使用时,您可以将其配置为将DDS样本存储到关系数据库中,例如MyS…...

MongoDB
MongoDB 应用场景 在传统数据库(Mysql),在数据操作的 **High performance 对数据库高并发读写的需求、Hugu Storage 对海量数据的高效率存储和访问的需求、High Scalability && High Availability 对数据库高扩展和高可用性的需…...
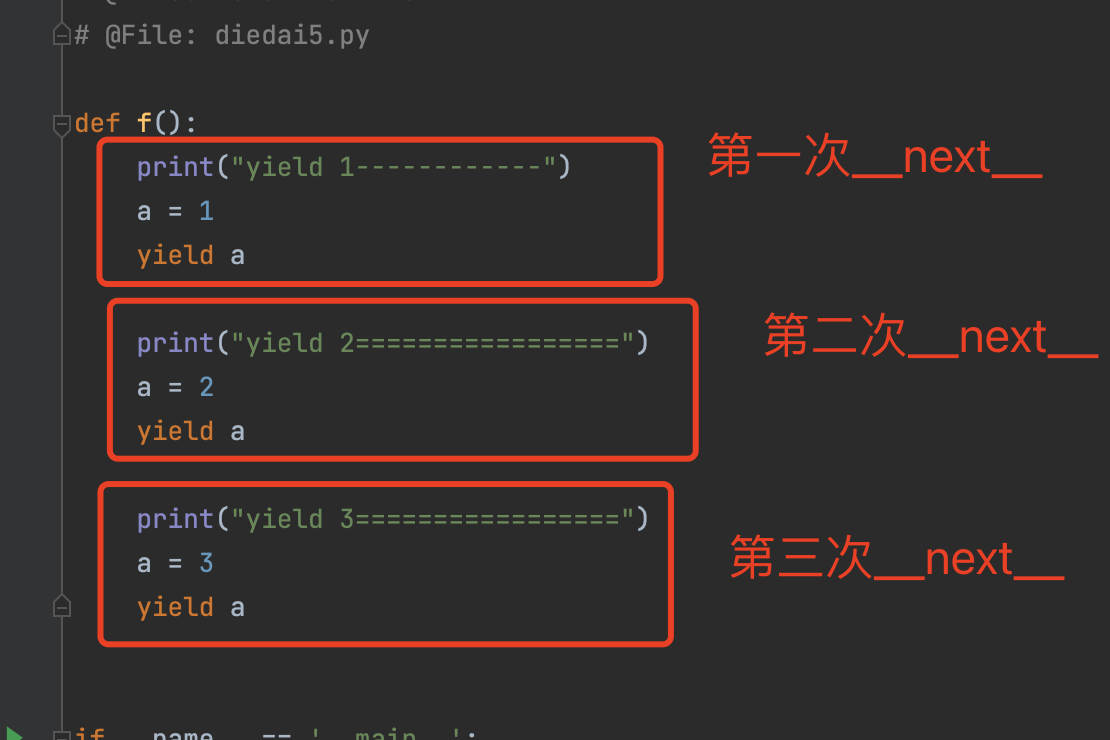
python 迭代器生成器
目录 一、可迭代对象 1.1 判断是否为可迭代对象 二、迭代器 2.1 判断对象是否是一个迭代器 2.2 手写一个迭代器 2.3 迭代器应用场景 三、生成器 3.1 生成器介绍 3.2 使用yield 关键字 生成器,来实现迭代器 3.3 生成器(yield关键字)…...

Iceberg基于Spark MergeInto语法实现数据的增量写入
SPARK SQL 基本语法 示例SQL如下 MERGE INTO target_table t USING source_table s ON s.id t.id //这里是JOIN的关联条件 WHEN MATCHED AND s.opType delete THEN DELETE // WHEN条件是对当前行进行打标的匹配条件 WHEN MATCHED AND s.opType update THEN…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...
