一个概率论例题引发的思考
浙江大学版《概率论与梳理统计》一书中的,第13章第1节例2如下:

这个解释和模型比较简单易懂。接下来,第2节的例2是一个关于此模型的题目:

在我自己的理解中,此题的解法跟上一个题目一样,第二级传输后,一共有4中可能性,按照平均概率相加即可。
{ p n q n q n p n } \begin {Bmatrix} p^n & q^n \\ q^n & p^n \end{Bmatrix} {pnqnqnpn}
然而,仔细考虑之后发现不妥。因为最后结果的概率,这样计算不太合适,但是又没有发现更合理的理论和方法,又看到这一节的如下论述:


似乎抓到了什么,但是又特别模糊。
再看以下C-K方程:

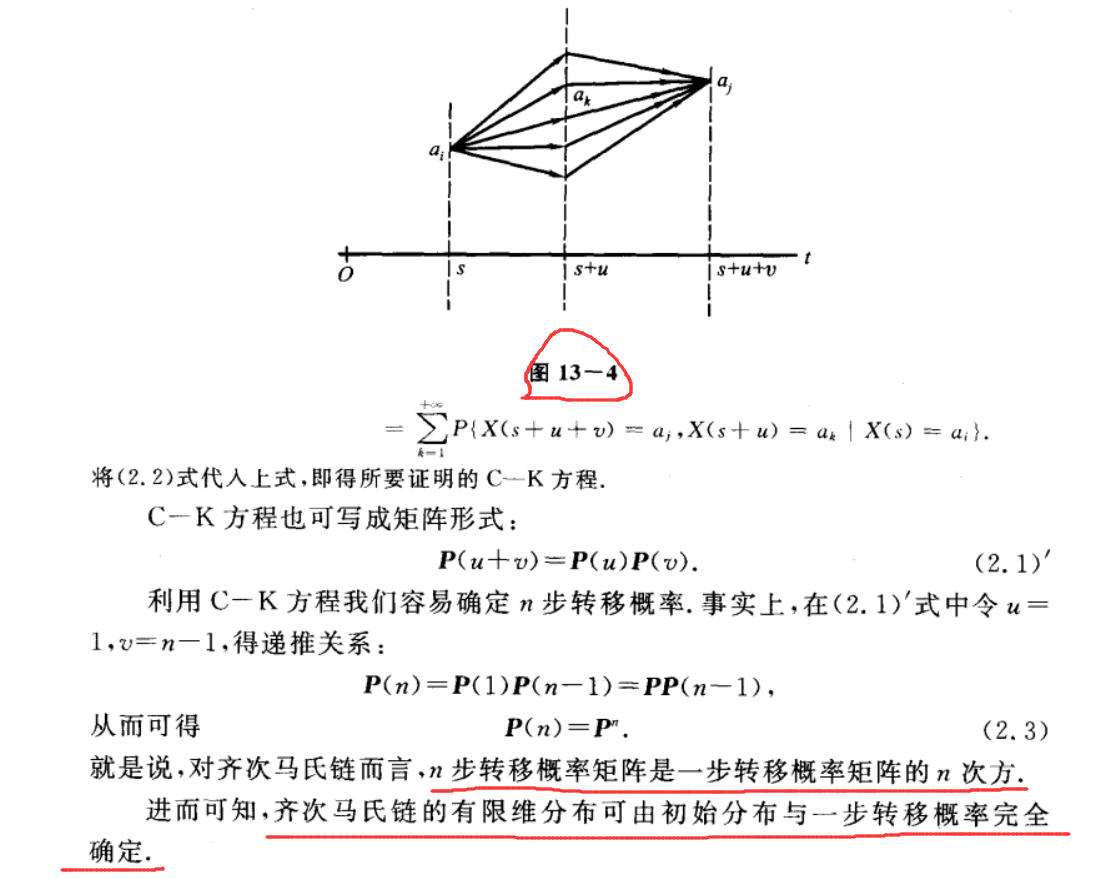
因此,参考此文:https://blog.csdn.net/m0_37567738/article/details/132182007?spm=1001.2014.3001.5502可以得出结论,此种题目的解题方法还是要回到马尔可夫概率转移矩阵中去找答案。
我觉得要理解此题目的底层逻辑,还需要了解以下公式:
P { X n = a n } = ∑ i = 1 + ∞ P { X n = a n , X 0 = a i } = ∑ i = 1 + ∞ P { X n = a n ∣ X 0 = a i } P { X 0 = a i } = ∑ i = 1 + ∞ P i ( 0 ) P i j ( n ) = ∑ i = 1 + ∞ P i 1 ( 1 ) P i j ( n − 1 ) = ∑ i = 1 + ∞ P 2 i ( 2 ) P i j ( n − 2 ) = ∑ i = 1 + ∞ P 3 i ( 3 ) P i j ( n − 3 ) = . . . . . . P \{X_n = a_n\} = \sum_{i = 1}^{+\infty} P\{ X_n = a_n, X_0 = a_i \} = \\ \sum_{i = 1}^{+\infty} P\{ X_n = a_n|X_0 = a_i \} P\{ X_0 = a_i \}=\sum_{i=1}^{+\infty} P_i(0) P_{ij}(n) = \\ \sum_{i=1}^{+\infty} P_{i1}(1) P_{ij}(n-1)= \sum_{i=1}^{+\infty} P_{2i}(2) P_{ij}(n-2) = \sum_{i=1}^{+\infty} P_{3i}(3) P_{ij}(n-3) = ...... \\ P{Xn=an}=i=1∑+∞P{Xn=an,X0=ai}=i=1∑+∞P{Xn=an∣X0=ai}P{X0=ai}=i=1∑+∞Pi(0)Pij(n)=i=1∑+∞Pi1(1)Pij(n−1)=i=1∑+∞P2i(2)Pij(n−2)=i=1∑+∞P3i(3)Pij(n−3)=......
这个逻辑的本质区别就在于,它是利用后验概率去推算先验概率的,这是一种理论上的优越性。
我们想要求解的概率P,它依赖于其概率矩阵的乘法运算,而不是说简单把4种转换相加。
相关文章:

一个概率论例题引发的思考
浙江大学版《概率论与梳理统计》一书中的,第13章第1节例2如下: 这个解释和模型比较简单易懂。接下来,第2节的例2是一个关于此模型的题目: 在我自己的理解中,此题的解法跟上一个题目一样,第二级传输后&…...
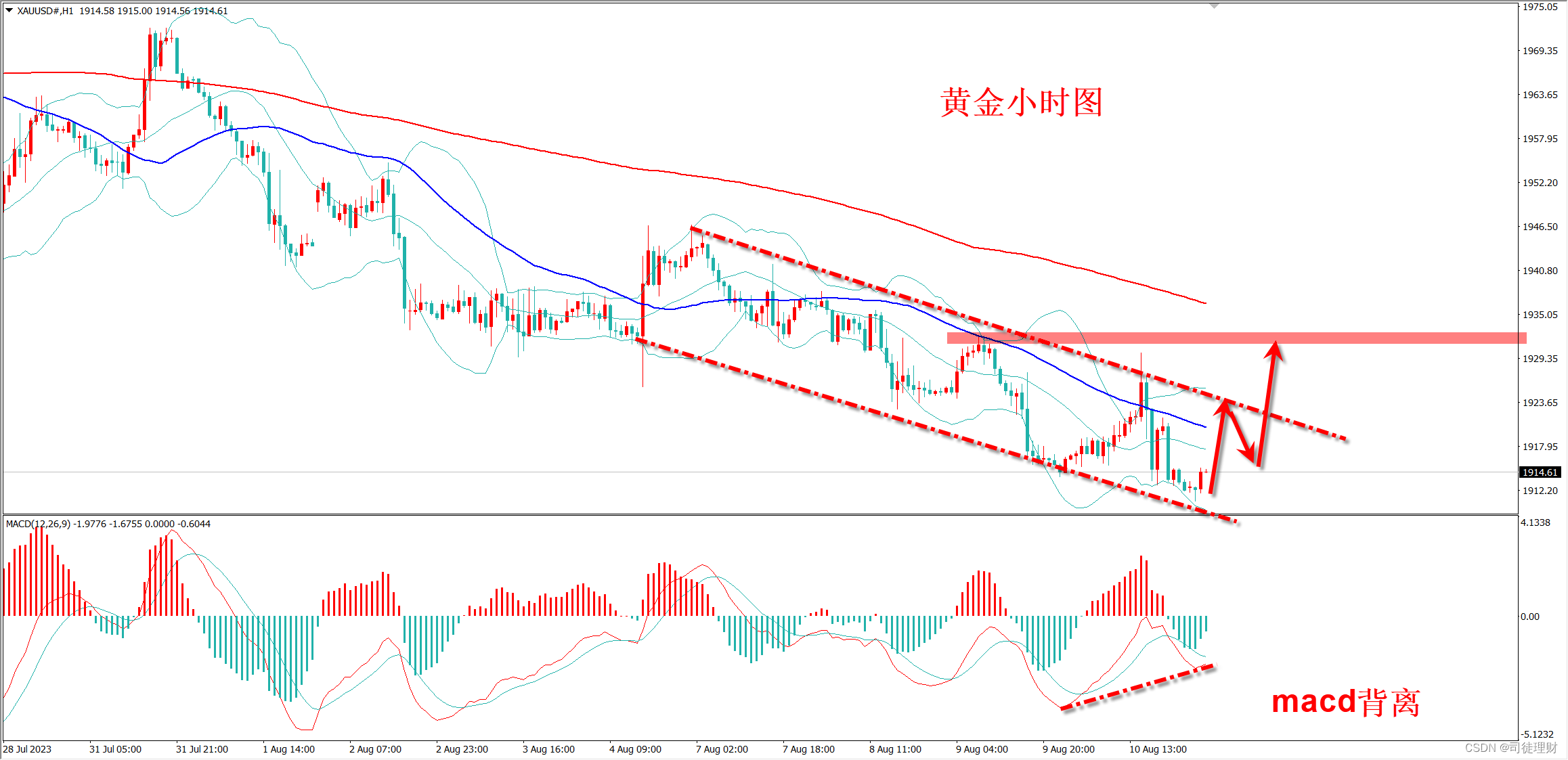
司徒理财:8.11黄金最新走势分析早盘1914现价多
黄金昨日再次破位新低,但是下跌力度出现衰竭迹象,意味着本次下跌暂时告一段落,行情将会开启一波反弹,早盘1914现价直接多,先看反弹上涨!黄金从走势上看,日线上已经跌至前低附近,也是…...

请写一个非对称加密工具 示例包括完整的通信流程
非对称加密工具通常用于保护数据的机密性和身份验证。下面是一个简化的示例,展示了完整的通信流程,包括密钥生成、加密、解密和数字签名验证: import java.security.KeyPair; import java.security.KeyPairGenerator; import java.security.…...
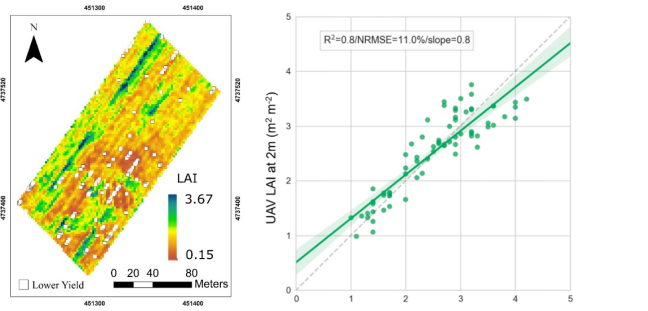
近地面无人机植被定量遥感与生理参数反演技术
遥感(RS-Remote Sensing)——不接触物体本身,用传感器收集目标物的电磁波信息,经处理、分析后,识别目标物,揭示其几何、物理性质和相互关系及其变化规律的现代科学技术。 换言之,即是“遥远的感…...

卡巴斯基为基于Linux的嵌入式设备推出专用解决方案
导读卡巴斯基在其卡巴斯基嵌入式系统安全产品中引入了对 Linux 的支持。这种适应性强的多层解决方案现在为基于Linux的嵌入式系统、设备和场景提供优化的安全,合通常适用于这些系统的严格监管标准。 卡巴斯基在其卡巴斯基嵌入式系统安全产品中引入了对 Linux 的支持…...

Word转PDF工具哪家安全?推荐好用的文件格式转换工具
Word文档是我们最常见也是最常用的办公软件,想必大家都知道了Word操作起来十分的简单,而且功能也是比较齐全的。随着科技的不断进步,如今也是有越来越多类型的办公文档,PDF就是其中之一,那么word转pdf怎么转?Word转PD…...

dma_mmap_coherent函数的使用
dma_mmap_coherent函数可以将dma地址映射到用户态,通过应用程序直接操作dma地址。 实现应该分配一段dma地址,例如: buf_addr dmam_alloc_coherent(&pdev->dev, size, &dma_addr, GFP_KERNEL);buf_addr 是内核态的虚拟地址&…...

MySQL_DQL语句(查询语句以及常用函数)
基础查询 不带条件的查询查询多个字段 语法: #查询指定字段的数据 SELECT 字段1, 字段2, 字段3 ... FROM 表名 ; #查询表中全部字段的数据 SELECT * FROM 表名 ;案例:查询表中所有信息数据 SELECT * FROM employee;案例:查询表中姓名和性别…...
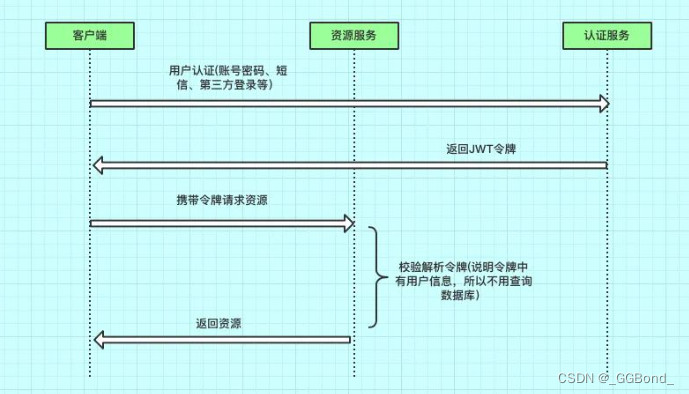
一步步教你实现JWT认证和授权
一步步教你实现JWT认证和授权 前言一、引入二、Token认证与JWT认证的关系三、什么是JWT认证?四、JWT的组成1、头部(Header)2、载荷(Payload)3、签名(Signature) 五、JWT认证的工作流程六、代码举…...

【python 深度学习】解决遇到的问题
目录 一、RuntimeError: module compiled against API version 0xc but this version of numpy is 0xb 二、AttributeError: module ‘tensorflow’ has no attribute ‘flags’ 三、conda 更新 Please update conda by running 四、to search for alternate channels that…...

maxwell 基于zookeeper的高可用方案
Maxwell版本1.39.2 一: 添加zk的pox文件 <!-- customize HA --> <dependency><groupId>org.apache.curator</groupId><artifactId>curator-framework</artifactId><version>5.4.0</version> </dependency>&…...
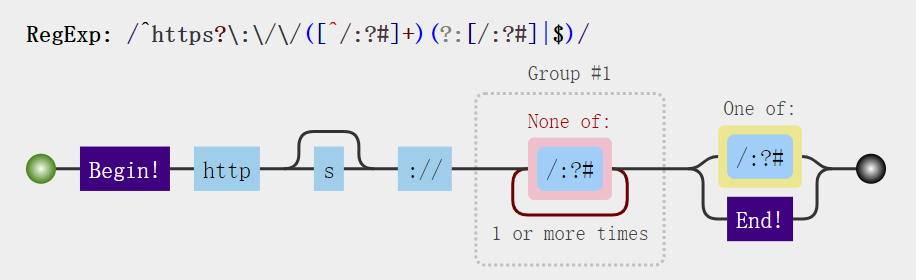
【JavaScript】match用法 | 正则匹配
match正则匹配 var e "www.apple.com:baidu.com" var match e.match(/com/g) console.log("match: "match);> "match: com,com"match返回值问题 match的返回值是一个数组 数组的第0个元素是与整个正则表达式匹配的结果 数组的第1个元素是…...

前端css + js +vue +element-ui 实现响应式布局,根据浏览器窗体大小自动响应
前端css js vue element-ui 实现响应式布局,根据浏览器窗体大小自动响应 1、环境2、js代码3、代码解释1、定义对象2、定义方法3、监听窗口变化,计算比例值,并赋值给transform 属性4、实现监听 3、html 代码4、特别注意 1、环境 我的环境是e…...
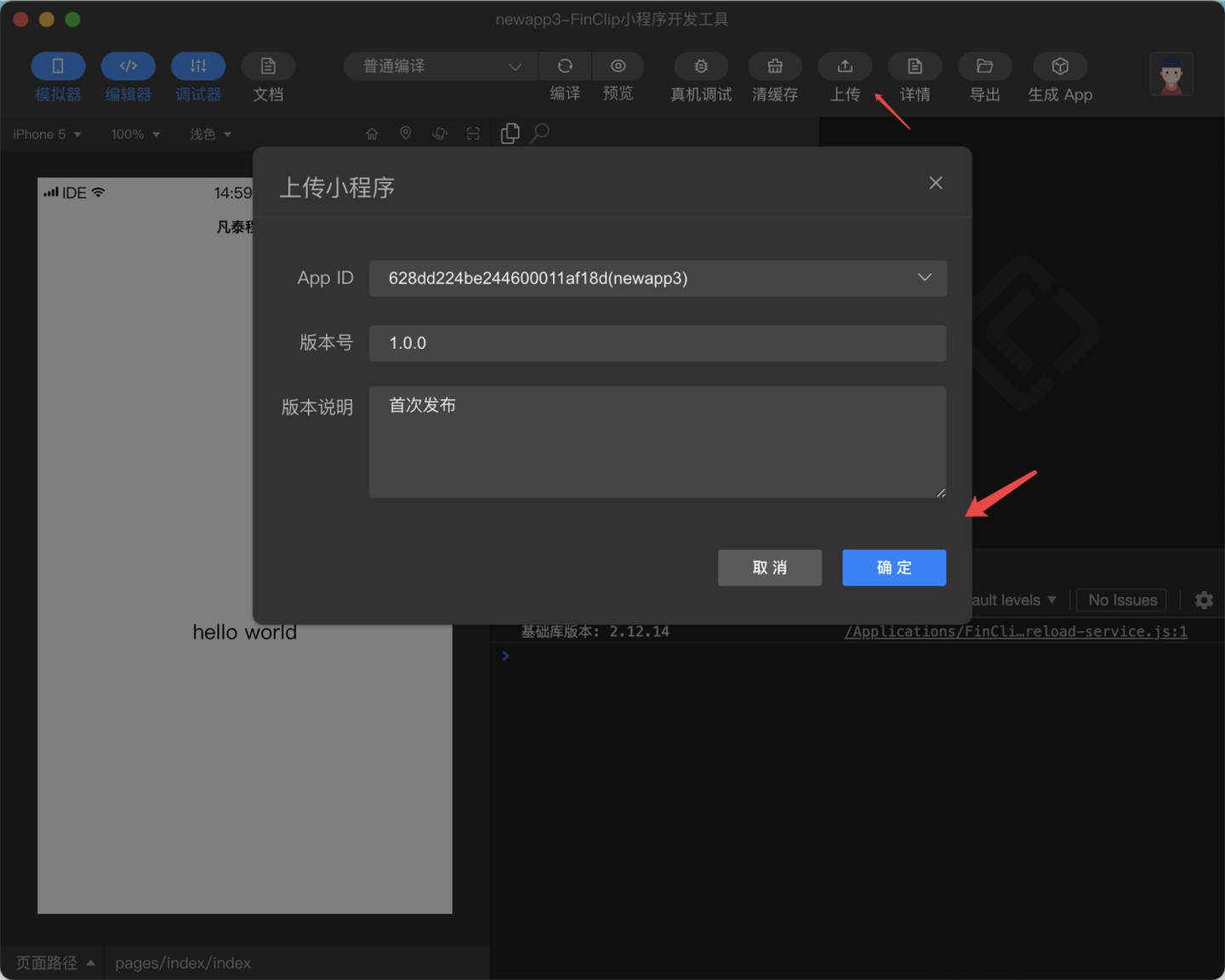
小程序生成App:轻量低门槛的开发方式
小程序生成App可以成为一种轻量低门槛的开发App的方式,但是需要根据具体情况进行选择。如果应用需要处理大量数据或需要进行复杂计算,或者需要实现原生特有的功能或交互效果,可能需要选择其他开发方式。 在文章开始之前,我们看看目…...
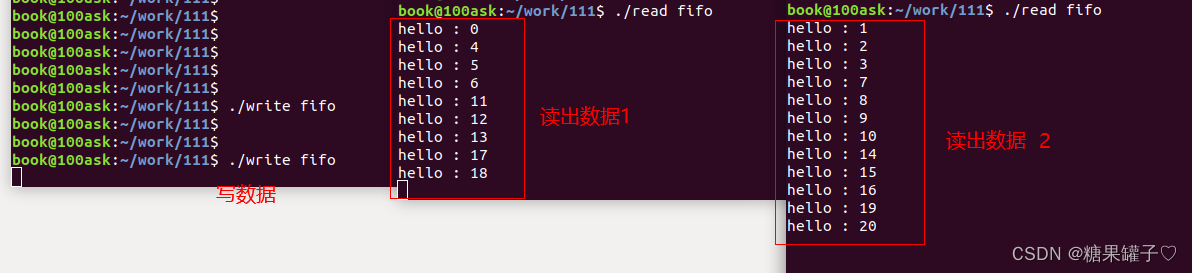
Linux命名管道进程通信
文章目录 前言一、什么是命名管道通信二、创建方式三、代码示例四、文件进程通信总结 前言 命名管道 是实现进程间通信的强大工具,它提供了一种简单而有效的方式,允许不同进程之间进行可靠的数据交换。不仅可以在同一主机上的不相关进程间进行通信&…...
如何将苹果彻底删除视频找回?试试这3种方法
如今是短视频时代,大家通常会使用苹果手机来拍摄视频,以此记录生活中的美好日常。但是大家都知道视频是十分占空间的,这也经常会出现iPhone内存不足,磁盘崩溃的问题。 当遇到iPhone内存不足的情况时,大家往往会选择清…...
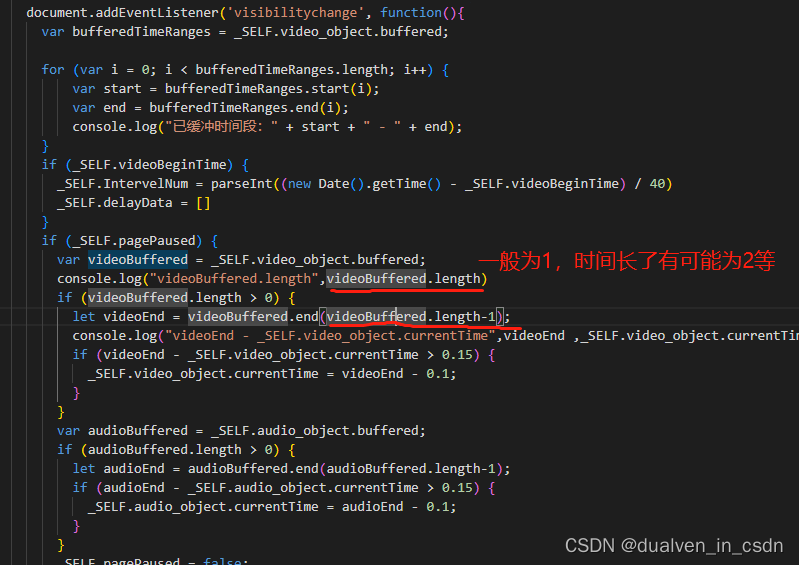
【音视频、chatGpt】h5页面最小化后,再激活后视频停住问题的解决
目录 现象 观察 解决 现象 页面有时候要切换,要最小化;短时间或者几个小时内切换回来,视频可以正常续上;而放置较长时间,几个小时或者一晚上,切换回来后,视频可能卡死 观察 切换页面&#x…...

[CSS] 图片九宫格
效果 index.html <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"/><meta http-equiv"X-UA-Compatible" content"IEedge"/><meta name"viewport" content"widthdevice-…...
MChat-Gpt V1.0.0 (将ChatGpt机器人接入内网供全体使用)
Github>https://github.com/MartinxMax/MChat-Gpt 首页 MChat-Gpt V1.0.0将ChatGpt机器人接入内网供全体使用 你需要一个ChatGpt账户如果您在中国则需要使用代理访问,设置TUN代理模式 安装依赖 选择你的系统进行安装 服务端配置 #python3 ChatGpt_Server.py -h 使用&a…...
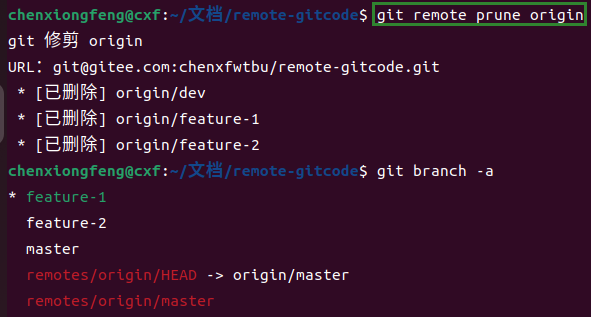
日常开发中Git命令指北
Git基本操作 创建化仓库 mkdir 目录 cd 目录 git init配置本地仓库 # 配置用户名,邮箱 git config user.name "cxf" git config user.email "1969612859qq.com" # 查看本地配置(小写的 L) git config -l # 重置配置&a…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...

麒麟系统使用-进行.NET开发
文章目录 前言一、搭建dotnet环境1.获取相关资源2.配置dotnet 二、使用dotnet三、其他说明总结 前言 麒麟系统的内核是基于linux的,如果需要进行.NET开发,则需要安装特定的应用。由于NET Framework 是仅适用于 Windows 版本的 .NET,所以要进…...
