代码随想录算法训练营第45天动态规划 背包基础 1 2、 416. 分割等和子集
文章目录
- 01背包基础 (二维数组)
- 思路
- 递推公式
- 初始化
- 遍历顺序
- 一维dp数组(滚动数组)
- 一维数组的递推公式
- 遍历顺序
- LeetCode 416. 分割等和子集
- 思路
- 总结
01背包基础 (二维数组)
思路
根据动态规划五部进行分析,先进行参数和下标的初始化
由于是背包探索我们用二维数组 创建一个 dp[i][j] i是指第几个书包,j是指背包最多能容下的体积
然后确定递推公式
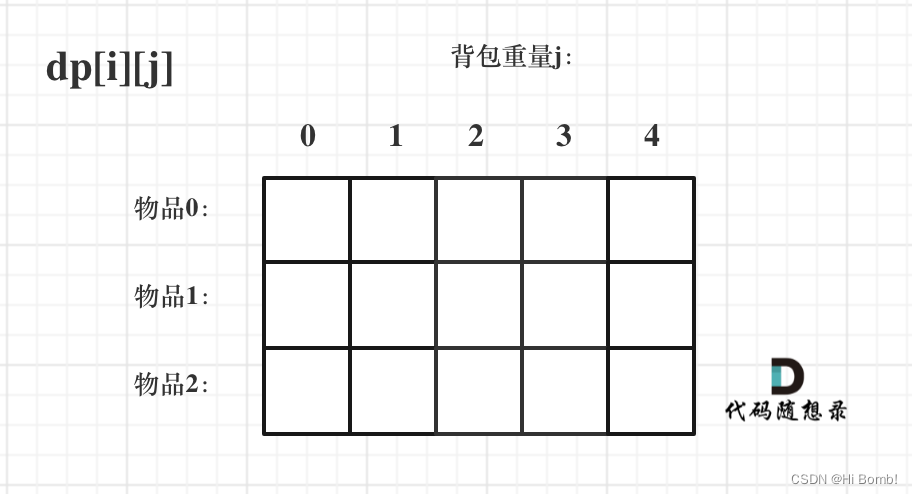
递推公式
这道题递推公式的展开从两个方面 一个是尺寸比书包小可以放进去 一个是尺寸比书包放不进去
- 不放物品i:
由dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以被背包内的价值依然和前面相同。) - 放物品i
由dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]]为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i](物品i的价值),就是背包放物品i得到的最大价值
所以递归公式:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
初始化
首先从dp[i][j]的定义出发,如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0。
// 正序遍历
for (int j = weight[0]; j <= bagweight; j++) {dp[0][j] = value[0];
}
遍历顺序
在二维数组中无论是先遍历物品 后遍历背包 或者 先遍历背包后遍历物品都能够达成目的
不过在后序的一维数组中完成背包问题就固定下来了, 先遍历物品后遍历书包。
一维dp数组(滚动数组)
在使用二维数组的时候,递推公式:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
其实可以发现如果把dp[i - 1]那一层拷贝到dp[i]上,表达式完全可以是:
dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);
与其把dp[i - 1]这一层拷贝到dp[i]上,不如只用一个一维数组了,只用dp[j](一维数组,也可以理解是一个滚动数组)。
一维数组的递推公式
dp[j]可以通过dp[j - weight[i]]推导出来,dp[j - weight[i]]表示容量为j -
weight[i]的背包所背的最大价值。dp[j - weight[i]] + value[i] 表示 容量为 j - 物品i重量 的背包 加上
物品i的价值。(也就是容量为j的背包,放入物品i了之后的价值即:dp[j])此时dp[j]有两个选择,一个是取自己dp[j] 相当于 二维dp数组中的dp[i-1][j],即不放物品i,一个是取dp[j -
weight[i]] + value[i],即放物品i,指定是取最大的,毕竟是求最大价值,
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
遍历顺序
与二维数组不同, 先物品再背包, 背包遍历要求 倒序遍历因为这样就可以保证每一个物品只放一次
for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}
}
LeetCode 416. 分割等和子集
思路
这里运用了 01背包的思路 ,我的做法是采用了一维数组的方式做的
class Solution {public boolean canPartition(int[] nums) {if(nums==null|| nums.length==0) return false;int n=nums.length;int sum=0;for(int num: nums){ sum+= num;}if( sum%2!=0) return false;int target= sum/2;int dp[]= new int [target+1];for( int i=0;i<n;i++){for( int j=target;j>= nums[i];j--){dp[j]= Math.max( dp[j],dp[j-nums[i]]+nums[i]);}}return dp[target] == target;}
}
总结
恢复更新了,之前在返校,临开学也没有状态就休息了一段时间
相关文章:

代码随想录算法训练营第45天动态规划 背包基础 1 2、 416. 分割等和子集
文章目录01背包基础 (二维数组)思路递推公式初始化遍历顺序一维dp数组(滚动数组)一维数组的递推公式遍历顺序LeetCode 416. 分割等和子集思路总结01背包基础 (二维数组) 思路 根据动态规划五部进行分析&a…...
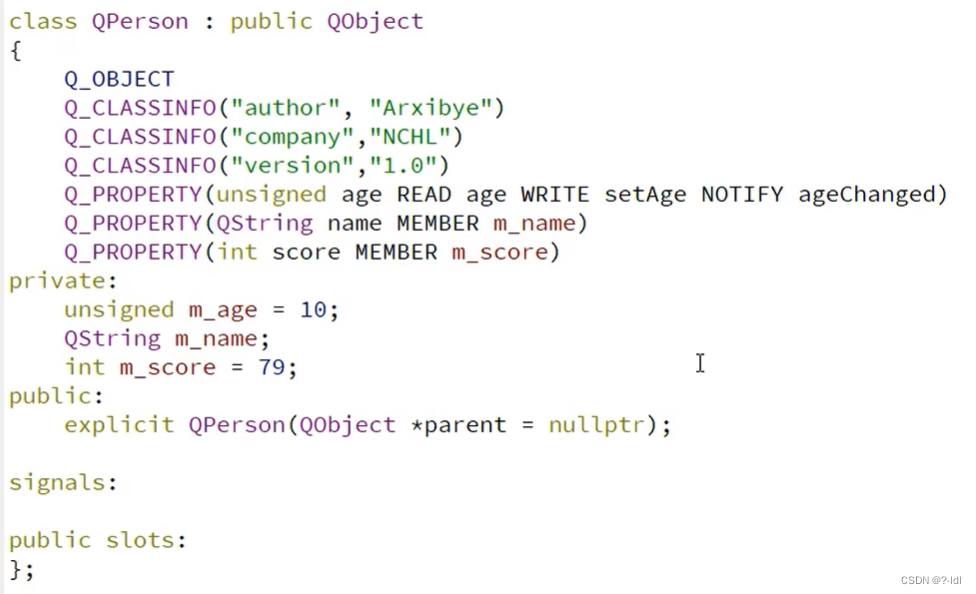
QT学习记录(六)类对象属性
类对象属性用来描述类对象的一些信息和当前的状态。类对象属性可以由类的编写者在编写类的时候定义,也可以由类的使用者在使用对象的时候定义。 由类的编写者定义 QPROPERTY()宏就是用来定义一个对象属性。 以第二行属性举例 QPROPERTY(bool enabled READ isEnabl…...

Spring Cloud Alibaba从搭建到源码完整进阶教程
微服务简介 Spring Cloud Alibaba 微服务简介 Nacos注册中心配置中心 Spring Cloud Nacos实战(一)- 下载和安装 Spring Cloud Nacos实战(二)- 服务提供者注册 Spring Cloud Nacos实战(三)- 服务消费者…...
Spring Cloud Nacos实战(一)- 下载和安装
Spring Cloud Alibaba Nacos下载和安装 Nacos介绍 Nacos(Naming Configuration Service) 是一个易于使用的动态服务发现、配置和服务管理平台,用于构建云原生应用程序 服务发现是微服务架构中的关键组件之一。Nacos 致力于帮助您发现…...
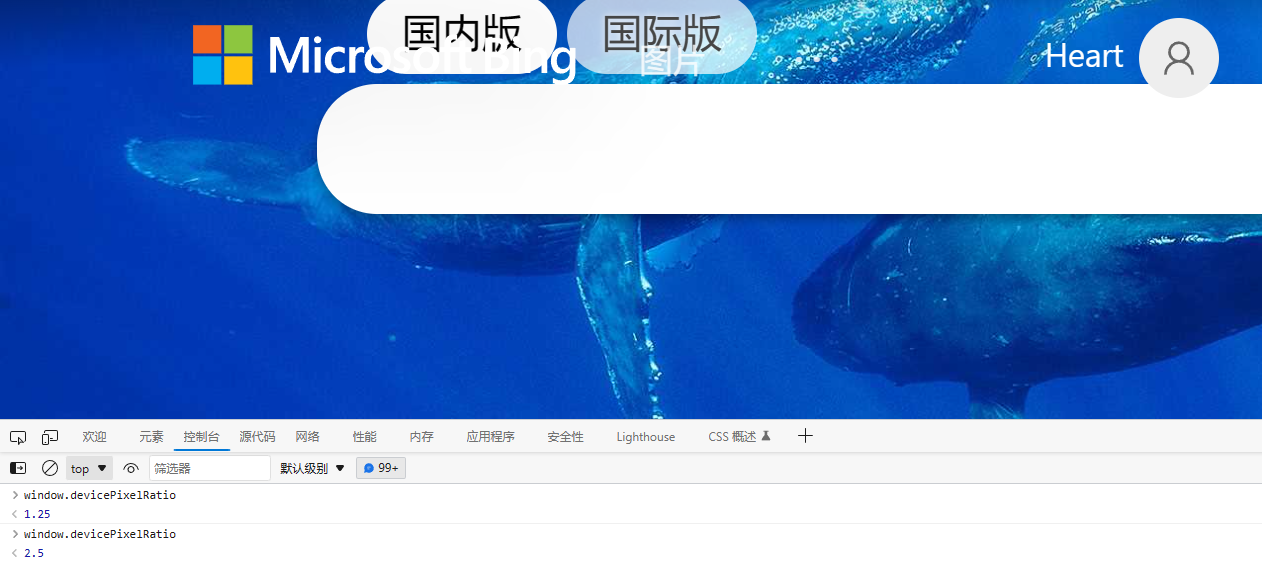
深入理解设备像素比
文章目录参考描述像素分辨率显示分辨率图像分辨率物理分辨率分辨率单位(仅部分)DPIPPI设备像素比设备物理像素设备独立像素设备像素比产生放大与缩小尾声参考 项目描述关于物理像素、逻辑像素(css像素)、分辨率、像素比的超详细讲…...
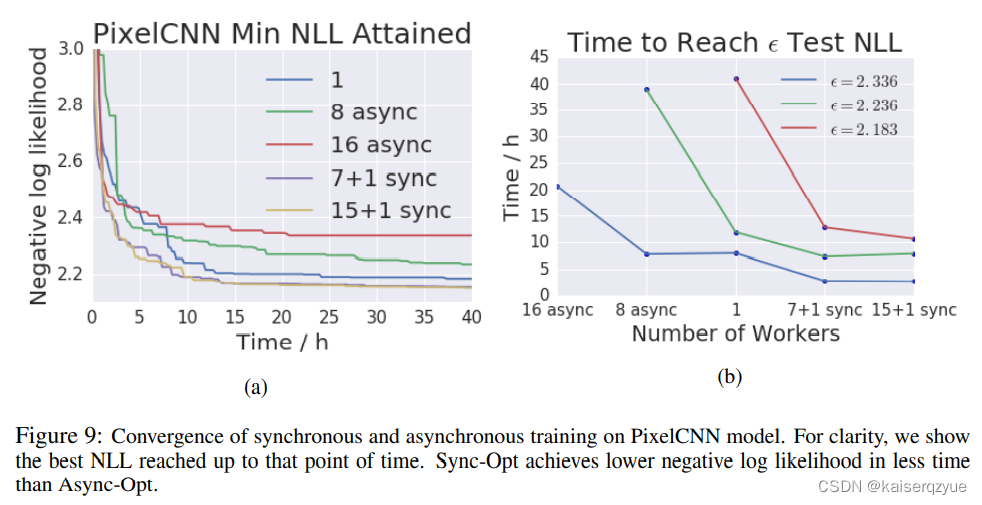
Revisiting Distributed Synchronous SGD 带有Back-up机制的分布式同步SGD方法 论文精读
论文链接:Revisiting Distributed Synchronous SGD ABS 本文介绍了用于分布式机器学习的同步和异步SGDSGDSGD,同时指出各自的缺点:stragglersstragglersstragglers和stalenessstalenessstaleness。 同时为了解决同步SGDSGDSGD存在straggle…...
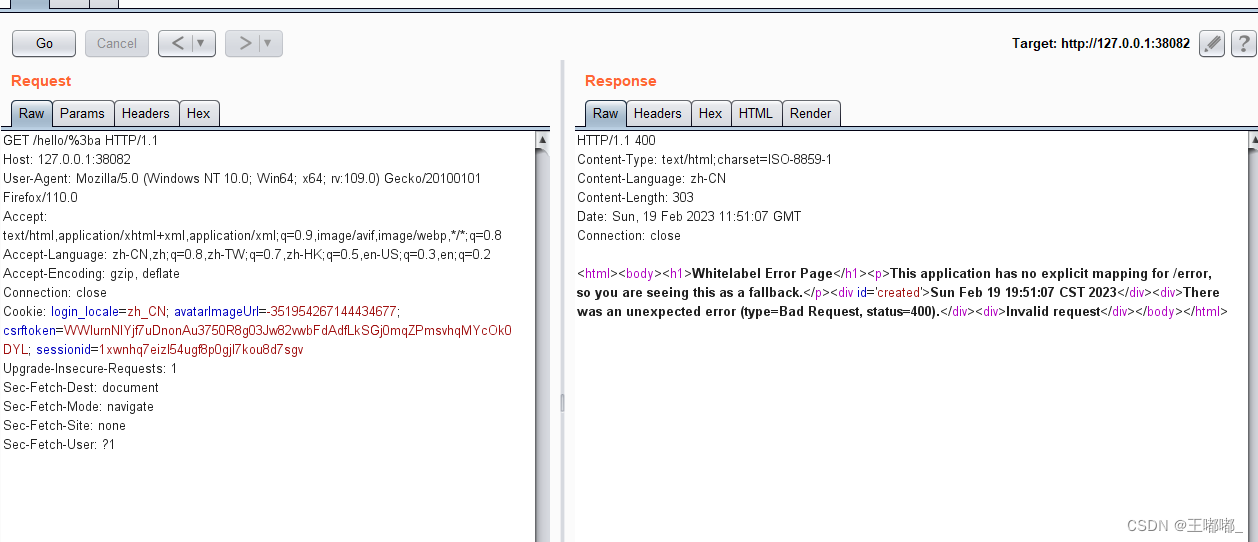
shiro CVE-2020-13933
0x00 前言 同CVE-2020-1957,补充一下笔记,在CVE-2020-1957的基础上进行了绕过。 影响版本:Apache Shiro < 1.6.0 环境搭建参考:shiro CVE-2020-1957 0x01 漏洞复现 CVE-2020-13933中使用%3b绕过了shiro /*的检测方式&…...

斐波那契数列(递归+迭代)
目录什么是斐波那契数列递归写法使用递归写法的缺点迭代写法(效率高)什么是斐波那契数列 斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多斐波那契(Leonardo Fibonacci)以兔子繁殖为例…...
2022黑马Redis跟学笔记.实战篇(六)
2022黑马Redis跟学笔记.实战篇 六4.7.达人探店功能4.7.1.分享探店图文1. 达人探店-发布探店笔记2. 达人探店-查看探店笔记4.7.2.点赞功能4.7.3.基于List实现点赞用户列表TOP104.7.4.基于SortedSet实现点赞排行榜4.8.关注列表4.8.1.关注列表实现原理4.8.2.添加关注1. 好友关注-关…...
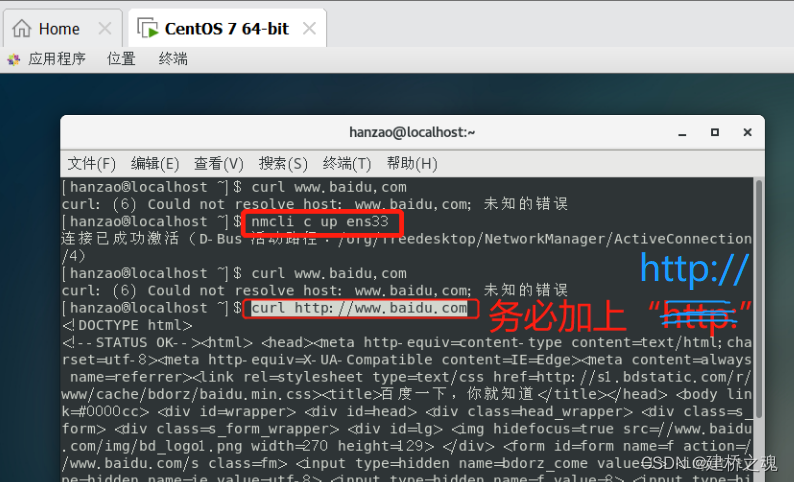
Linux-VMware常用设置(时间+网络)及网络连接激活失败解决方法-基础篇②
目录一、设置时间二、网络设置1. 激活网卡方法一:直接启动网卡(仅限当此)方法二:修改配置文件(永久)2. 将NAT模式改为桥接模式什么是是NAT模式?如何改为桥接模式?三、虚拟机网络连接…...

vue3学习总结1
一.vue3与vue2相比带来哪些变化?a.性能的提升(包括打包大小减少,初次渲染的速度加快,更新渲染速度加快,内存减少)b.源码的升级(响应式的原理发生了变化,由原来的defineProperty变成了…...
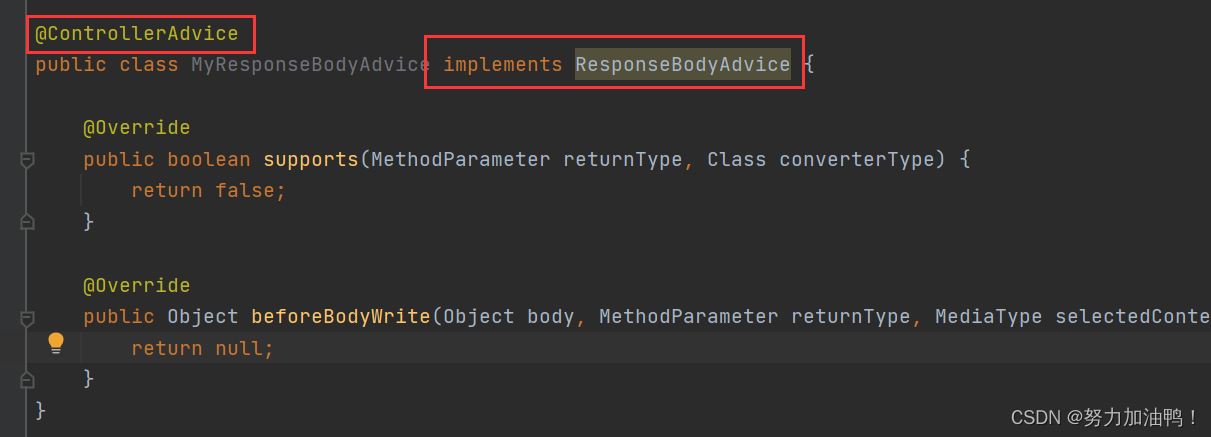
SpringBoot统一功能处理
一、统一用户登录权限验证 1.1Spring拦截器 实现拦截器需要以下两步: 1.创建自定义拦截器,实现 HandlerInterceptor 接⼝的 preHandle(执行具体方法之前的预处理)方法。 2.将⾃定义拦截器加⼊ WebMvcConfigurer 的 addIntercept…...
答案解析)
2022年3月电子学会Python等级考试试卷(五级)答案解析
目录 一、单选题(共25题,共50分) 二、判断题(共10题,共20分) 三、编程题(共3题,共30分) 青少年软件编程(Python)等级考试试卷(五级&#...

【C++】智能指针
目录 一、先来看一下什么是智能指针 二、 auto_ptr 1、C98版本 2、C11的auto_ptr 三、boost 库中的智能指针 1. scoped_ptr 2、shared_ptr(最好的智能指针) 四、C11中新提供的智能指针 unique_ptr shared_ptr std::shared_ptr的循环引用问题…...
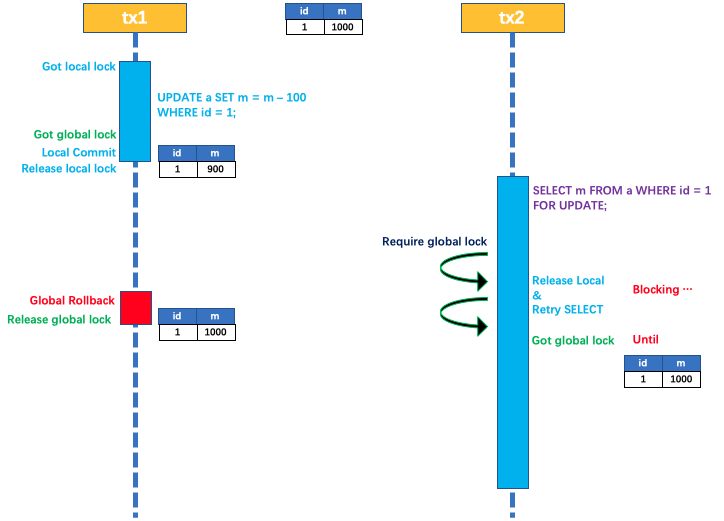
Seata架构篇 - AT模式
AT 模式 概述 Seata AT 模式是一种非侵入式的分布式事务解决方案,Seata 在内部做了对数据库操作的代理层,我们使用 Seata AT 模式时,实际上用的是 Seata 自带的数据源代理 DataSourceProxy,Seata 在这层代理中加入了很多逻辑&am…...
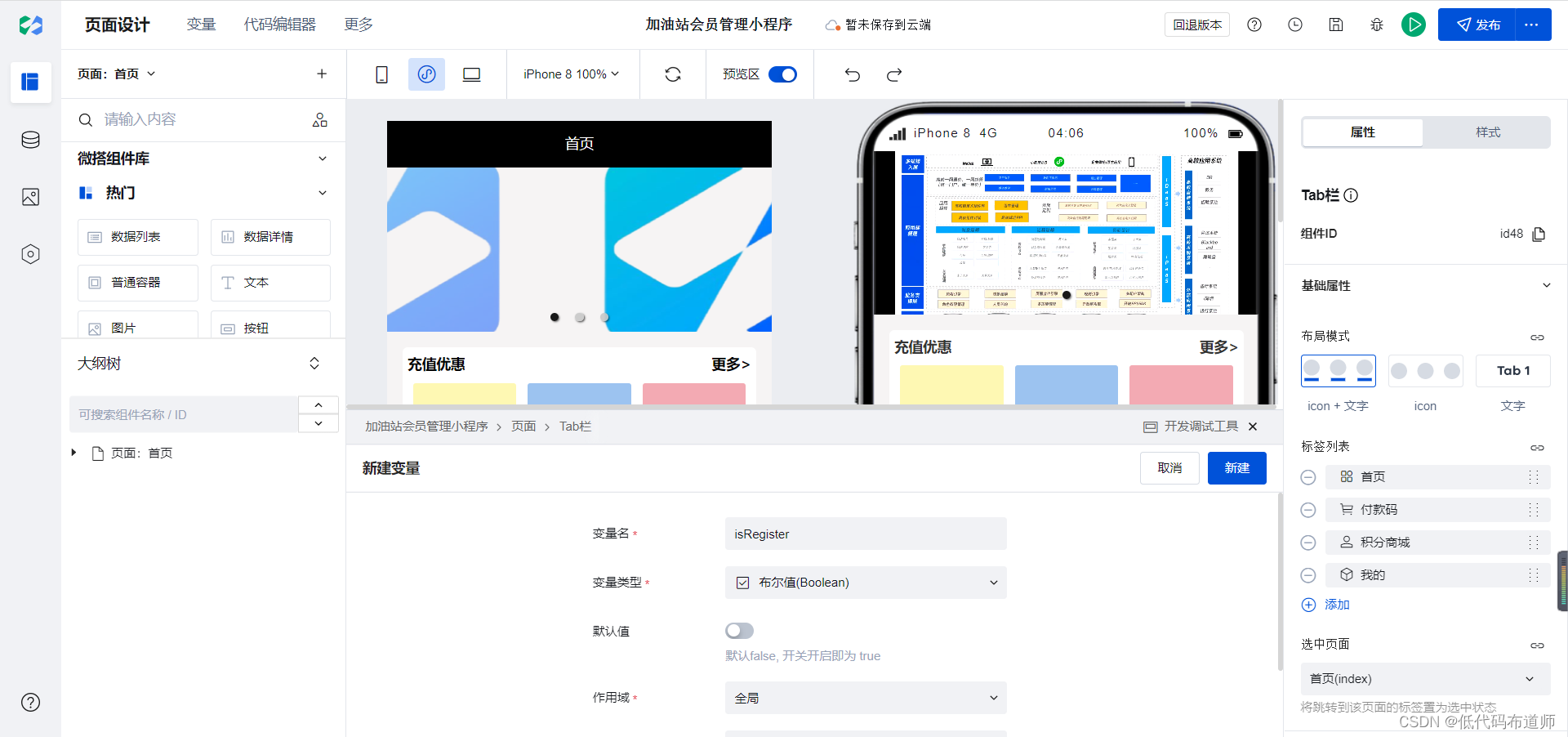
加油站会员管理小程序实战开发教程12
我们上一篇介绍了会员数据源的开发,本节我们介绍一下会员注册功能。 首先呢梳理一下会员注册的业务逻辑,如果用户是首次登录,那他肯定还没有给我们的小程序提交任何的信息。那么我们就在我的页面给他显示一个注册的按钮,如果他已经注册过了,那么就正常显示会员的信息,他…...
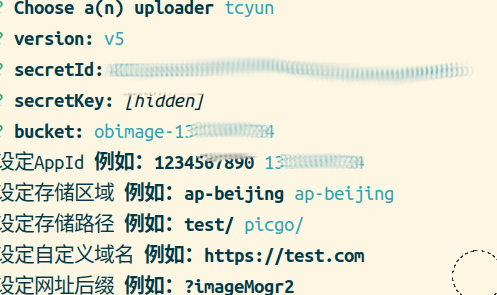
用腾讯云同步Obsidian笔记
介绍 之前用gitee同步OB笔记,同时做图床。但由于git系产品设置起来相对复杂,且后续可能有外链过审等问题。周五被同事小姐姐安利了用腾讯云COS,试了一下,果然不错。其主要优点如下: 设置简单,学习成本低&…...
浅析C++指针与引用,栈传递的关系
目录 前言 C 堆指针 栈指针 常量指针 指针常量 引用 常量引用 总结 前言 目前做了很多项目,接触到各种语言,基本上用什么学什么,语言的边际就会很模糊,实际上语言的设计大同小异,只是语言具备各自的特性区别。…...

图解LeetCode——剑指 Offer 10- II. 青蛙跳台阶问题
一、题目 一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。 答案需要取模 1e97(1000000007),如计算初始结果为:1000000008,请返回 1。 二、示例 2.1>…...

【Linux】用户分类+权限管理+umask+粘滞位说明
目录 1.用户分类 su指令 2.认识Linux权限 2.1 文件访问者的分类 2.2 文件类型和访问权限 a. 文件类型 file指令 b. 访问权限 2.3 文件权值的表示方法 a. 字母表示法 b. 八进制表示法 3.如何修改文件访问者的权限及相关指令 1. chmod指令 2. chown指令 3. chgrp指…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...
