Java数据结构-栈、队列常用类(Stack、ArrayDeque、LinkedLList)
数据结构的三要素包括:逻辑结构、存储结构、数据的运算。逻辑结构描述的是数据之间的逻辑关系,分为线性结构(线性表(数组、链表)、栈、队列)和非线性结构(图、树、集合)。物理结构也称为存储结构(顺序存储、链式存储、索引存储、散列存储)。
常见的数据结构分为线性数据结构和非线性数据结构,包括:数组、链表、栈、队列、树、图、散列表等。
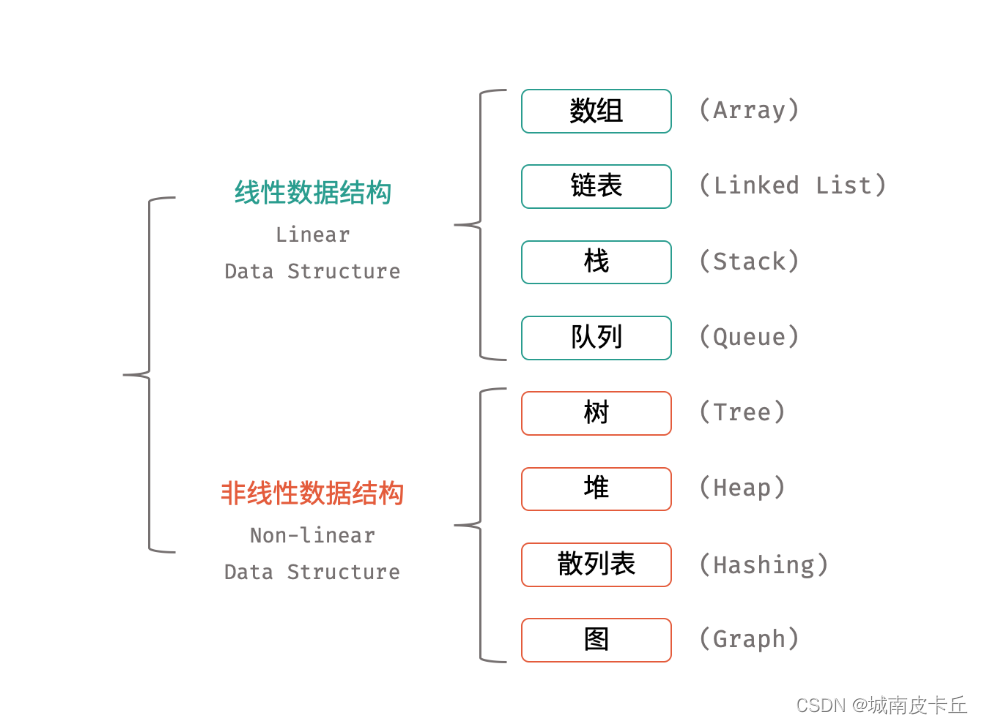
在Java中,数组这种数据结构有专门的实现:不可变数组(int [] array={})、可变数组(ArrayList),同样的链表这种数据结构也有专门的实现类(LinkedList),这些实现类都是java封装好的类,开箱即用。但是,java有没有专门针对于栈、队列这两种数据结构的封装类呢?
结果是肯定的。下面我们来介绍在java这门语言中,对栈、队列这两种数据结构的封装类。
一、栈(Stack、ArrayDeque、LinkedList)
首先来看一下JAVA集合体系图

Stack类,正如类名那样,该类是java对栈这种数据结构的封装,我们可以很容易滴使用该类中的方法实现栈的所有功能。下面是该类的五个方法
| 方法名 | 返回类型 | 说明 |
|---|---|---|
| empty | boolean | 判断是否为空 |
| peek | E | 只返回栈顶端的元素,不弹出该元素(空栈会抛出异常) |
| pop | E | 弹出栈顶的元素 |
| push | E | 将元素压入栈,并返回 |
| search | int | 返回最靠近顶端的目标元素到顶端的距离(调用 lastIndexOf) |
不过,由于Stack类是继承至Vector,Vector 类在方法上添加了 synchronized ,以达到线程安全的目的,不过 JVM 级别的 synchronized 特别消耗资源,已不被 Java 官方推荐使用。因此,用Stack类作为栈来使用已经不合时宜。
ArrayDeque类实现了Deque接口,而Deque接口又继承至Queue接口,Queue是一个单向队列,在头部进行remove()、poll()出队操作,在尾部进行add()、offer()入队操作,使用peek()、element()方法检索队列头。下面的表格给出了Queue接口的方法,
| boolean | add(E e) 将指定的元素插入到此队列中,如果可以立即执行此操作,而不会违反容量限制, true在成功后返回 IllegalStateException如果当前没有可用空间,则抛出IllegalStateException。 |
| E | element() 检索,但不删除,这个队列的头。 |
| boolean | offer(E e) 如果在不违反容量限制的情况下立即执行,则将指定的元素插入到此队列中。 |
| E | peek() 检索但不删除此队列的头,如果此队列为空,则返回 null 。 |
| E | poll() 检索并删除此队列的头,如果此队列为空,则返回 null 。 |
| E | remove() 检索并删除此队列的头。 |
Deque接口定义了双端队列,deque(double-ended queue,双端队列)是一种具有队列和栈的性质的数据结构,它允许两端都可以进行入和出队操作的队列,即元素可以从队头出队和入队,也可以从队尾出队和入队。因此。Deque即可当成队列使用,也可当成栈使用。下面是Deque中定义的方法:
| boolean | add(E e) 将指定的元素插入此双端队列表示的队列中(换句话说,在此双端队列的尾部),如果它是立即可行且不会违反容量限制,返回 true在成功时和抛出 IllegalStateException如果当前没有空间可用的。 |
| void | addFirst(E e) 插入此双端队列的前面,如果它是立即可行且不会违反容量限制,抛出一个指定的元素 IllegalStateException如果当前没有空间可用。 |
| void | addLast(E e) 在插入如果它是立即可行且不会违反容量限制,抛出此双端队列的末尾指定元素 IllegalStateException如果当前没有空间可用。 |
| boolean | contains(Object o) 如果此deque包含指定的元素,则返回 true 。 |
| Iterator<E> | descendingIterator() 以相反的顺序返回此deque中的元素的迭代器。 |
| E | element() 检索但不删除由此deque表示的队列的头部(换句话说,该deque的第一个元素)。 |
| E | getFirst() 检索,但不删除,这个deque的第一个元素。 |
| E | getLast() 检索,但不删除,这个deque的最后一个元素。 |
| Iterator<E> | iterator() 以正确的顺序返回此deque中的元素的迭代器。 |
| boolean | offer(E e) 将指定的元素插入由此deque表示的队列(换句话说,在该deque的尾部),如果可以立即执行,而不违反容量限制, true在成功时 false如果当前没有可用空间,则返回false。 |
| boolean | offerFirst(E e) 在此deque的前面插入指定的元素,除非它会违反容量限制。 |
| boolean | offerLast(E e) 在此deque的末尾插入指定的元素,除非它会违反容量限制。 |
| E | peek() 检索但不删除由此deque表示的队列的头部(换句话说,此deque的第一个元素),如果此deque为空,则返回 null 。 |
| E | peekFirst() 检索,但不删除,此deque的第一个元素,或返回 null如果这个deque是空的。 |
| E | peekLast() 检索但不删除此deque的最后一个元素,如果此deque为空,则返回 null 。 |
| E | poll() 检索并删除由此deque(换句话说,此deque的第一个元素)表示的队列的 null如果此deque为空,则返回 null 。 |
| E | pollFirst() 检索并删除此deque的第一个元素,如果此deque为空,则返回 null 。 |
| E | pollLast() 检索并删除此deque的最后一个元素,如果此deque为空,则返回 null 。 |
| E | pop() 从这个deque表示的堆栈中弹出一个元素。 |
| void | push(E e) 将元素推送到由此deque表示的堆栈(换句话说,在此deque的头部),如果可以立即执行此操作而不违反容量限制,则抛出 IllegalStateException如果当前没有可用空间)。 |
| E | remove() 检索并删除由此deque表示的队列的头(换句话说,该deque的第一个元素)。 |
| boolean | remove(Object o) 从此deque中删除指定元素的第一个出现。 |
| E | removeFirst() 检索并删除此deque的第一个元素。 |
| boolean | removeFirstOccurrence(Object o) 从此deque中删除指定元素的第一个出现。 |
| E | removeLast() 检索并删除此deque的最后一个元素。 |
| boolean | removeLastOccurrence(Object o) 从此deque中删除指定元素的最后一次出现。 |
| int | size() 返回此deque中的元素数。 |
ArrayDeque类实现了Deque接口 ,类内方法基本与Deque一致。不过ArrayDeque类的底层是一个环形数组,具体来说在逻辑结构上是一个环形,但是实际存储结构上是一个一维数组。
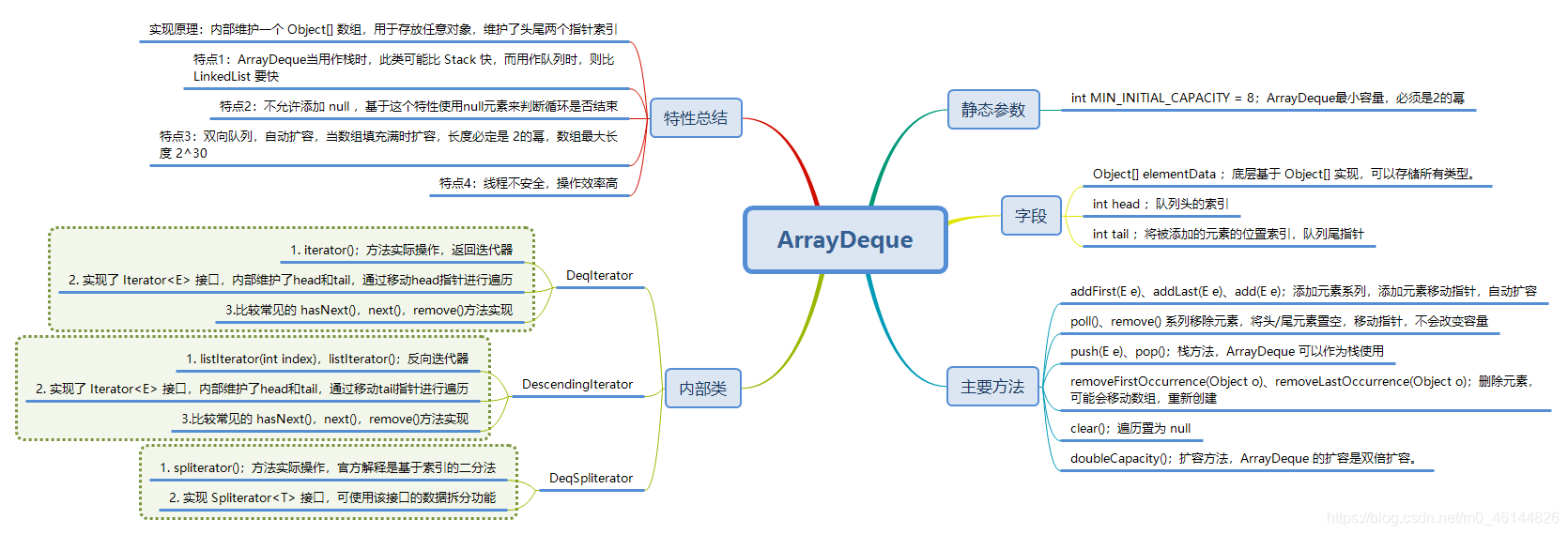
下面是该类的常用方法
| boolean | add(E e) 在此deque的末尾插入指定的元素。 |
| void | addFirst(E e) 在此deque前面插入指定的元素。 |
| void | addLast(E e) 在此deque的末尾插入指定的元素。 |
| void | clear() 从这个deque中删除所有的元素。 |
| ArrayDeque<E> | clone() 返回此deque的副本。 |
| boolean | contains(Object o) 如果此deque包含指定的元素,则返回 true 。 |
| Iterator<E> | descendingIterator() 以相反的顺序返回此deque中的元素的迭代器。 |
| E | element() 检索,但不删除,由这个deque表示的队列的头。 |
| E | getFirst() 检索,但不删除,这个deque的第一个元素。 |
| E | getLast() 检索,但不删除,这个deque的最后一个元素。 |
| boolean | isEmpty() 如果此deque不包含元素,则返回 true 。 |
| Iterator<E> | iterator() 返回此deque中的元素的迭代器。 |
| boolean | offer(E e) 在此deque的末尾插入指定的元素。 |
| boolean | offerFirst(E e) 在此deque前面插入指定的元素。 |
| boolean | offerLast(E e) 在此deque的末尾插入指定的元素。 |
| E | peek() 检索但不删除由此deque表示的队列的头部,如果此deque为空,则返回 null 。 |
| E | peekFirst() 检索但不删除此deque的第一个元素,如果此deque为空,则返回 null 。 |
| E | peekLast() 检索但不删除此deque的最后一个元素,或返回 null如果此deque为空)。 |
| E | poll() 检索并删除由此deque(换句话说,该deque的第一个元素)表示的队列的 null如果此deque为空,则返回 null 。 |
| E | pollFirst() 检索并删除此deque的第一个元素,如果此deque为空,则返回 null 。 |
| E | pollLast() 检索并删除此deque的最后一个元素,如果此deque为空,则返回 null 。 |
| E | pop() 从这个deque表示的堆栈中弹出一个元素。 |
| void | push(E e) 将元素推送到由此deque表示的堆栈上。 |
| E | remove() 检索并删除由此deque表示的队列的头部。 |
| boolean | remove(Object o) 从此deque中删除指定元素的单个实例。 |
| E | removeFirst() 检索并删除此deque的第一个元素。 |
| boolean | removeFirstOccurrence(Object o) 删除此deque中指定元素的第一个出现(从头到尾遍历deque时)。 |
| E | removeLast() 检索并删除此deque的最后一个元素。 |
| boolean | removeLastOccurrence(Object o) 删除此deque中指定元素的最后一次(从头到尾遍历deque时)。 |
| int | size() 返回此deque中的元素数。 |
| Spliterator<E> | spliterator() 创建一个late-binding和失败快速 Spliterator在这个deque的元素。 |
| Object[] | toArray() 以适当的顺序返回一个包含此deque中所有元素的数组(从第一个到最后一个元素)。 |
| <T> T[] | toArray(T[] a) 以正确的顺序返回一个包含此deque中所有元素的数组(从第一个到最后一个元素); 返回的数组的运行时类型是指定数组的运行时类型。 |
LinkedList的底层维护了一个双向链表,它同时实现了List接口和Deque对口,因此它既可以看作一个顺序容器,又可以看作一个队列(Queue),同时又可以看作一个栈(stack),换句话说,它同时具备双向链表和双端队列特点。从继承图上来看,该类实现了Deque接口,因此可以使用接口中的方法。
| boolean | add(E e) 将指定的元素追加到此列表的末尾。 |
| void | add(int index, E element) 在此列表中的指定位置插入指定的元素。 |
| boolean | addAll(Collection<? extends E> c) 按照指定集合的迭代器返回的顺序将指定集合中的所有元素追加到此列表的末尾。 |
| boolean | addAll(int index, Collection<? extends E> c) 将指定集合中的所有元素插入到此列表中,从指定的位置开始。 |
| void | addFirst(E e) 在该列表开头插入指定的元素。 |
| void | addLast(E e) 将指定的元素追加到此列表的末尾。 |
| void | clear() 从列表中删除所有元素。 |
| Object | clone() 返回此 LinkedList的浅版本。 |
| boolean | contains(Object o) 如果此列表包含指定的元素,则返回 true 。 |
| Iterator<E> | descendingIterator() 以相反的顺序返回此deque中的元素的迭代器。 |
| E | element() 检索但不删除此列表的头(第一个元素)。 |
| E | get(int index) 返回此列表中指定位置的元素。 |
| E | getFirst() 返回此列表中的第一个元素。 |
| E | getLast() 返回此列表中的最后一个元素。 |
| int | indexOf(Object o) 返回此列表中指定元素的第一次出现的索引,如果此列表不包含元素,则返回-1。 |
| int | lastIndexOf(Object o) 返回此列表中指定元素的最后一次出现的索引,如果此列表不包含元素,则返回-1。 |
| ListIterator<E> | listIterator(int index) 从列表中的指定位置开始,返回此列表中元素的列表迭代器(按适当的顺序)。 |
| boolean | offer(E e) 将指定的元素添加为此列表的尾部(最后一个元素)。 |
| boolean | offerFirst(E e) 在此列表的前面插入指定的元素。 |
| boolean | offerLast(E e) 在该列表的末尾插入指定的元素。 |
| E | peek() 检索但不删除此列表的头(第一个元素)。 |
| E | peekFirst() 检索但不删除此列表的第一个元素,如果此列表为空,则返回 null 。 |
| E | peekLast() 检索但不删除此列表的最后一个元素,如果此列表为空,则返回 null 。 |
| E | poll() 检索并删除此列表的头(第一个元素)。 |
| E | pollFirst() 检索并删除此列表的第一个元素,如果此列表为空,则返回 null 。 |
| E | pollLast() 检索并删除此列表的最后一个元素,如果此列表为空,则返回 null 。 |
| E | pop() 从此列表表示的堆栈中弹出一个元素。 |
| void | push(E e) 将元素推送到由此列表表示的堆栈上。 |
| E | remove() 检索并删除此列表的头(第一个元素)。 |
| E | remove(int index) 删除该列表中指定位置的元素。 |
| boolean | remove(Object o) 从列表中删除指定元素的第一个出现(如果存在)。 |
| E | removeFirst() 从此列表中删除并返回第一个元素。 |
| boolean | removeFirstOccurrence(Object o) 删除此列表中指定元素的第一个出现(从头到尾遍历列表时)。 |
| E | removeLast() 从此列表中删除并返回最后一个元素。 |
| boolean | removeLastOccurrence(Object o) 删除此列表中指定元素的最后一次出现(从头到尾遍历列表时)。 |
| E | set(int index, E element) 用指定的元素替换此列表中指定位置的元素。 |
| int | size() 返回此列表中的元素数。 |
| Spliterator<E> | spliterator() 在此列表中的元素上创建late-binding和故障快速 Spliterator 。 |
| Object[] | toArray() 以正确的顺序(从第一个到最后一个元素)返回一个包含此列表中所有元素的数组。 |
| <T> T[] | toArray(T[] a) 以正确的顺序返回一个包含此列表中所有元素的数组(从第一个到最后一个元素); 返回的数组的运行时类型是指定数组的运行时类型。 |
由于LinkedList与ArrayDeque都是实现了Deque接口,因此这两个类中定义的方法几乎完全相同,因此这两个类的用法也几乎没有什么差异,虽然对于使用者而言,用这两个类都可以轻而易举的实现栈、队列的功能。
相关文章:

Java数据结构-栈、队列常用类(Stack、ArrayDeque、LinkedLList)
数据结构的三要素包括:逻辑结构、存储结构、数据的运算。逻辑结构描述的是数据之间的逻辑关系,分为线性结构(线性表(数组、链表)、栈、队列)和非线性结构(图、树、集合)。物理结构也…...
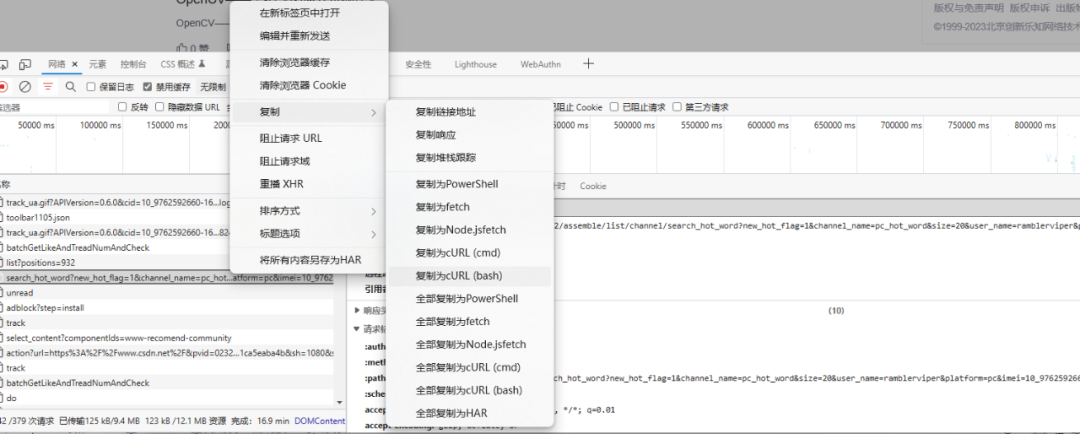
拯救了大批爬虫程序员,因为一个简单的神器
相信大家应该都写过爬虫,简单的爬虫只需要使用 requests 即可。遇到复杂的爬虫,就需要在程序里面加上请求头和参数信息。类似这种:我们一般的步骤是,先到浏览器的网络请求中找到我们需要的请求,然后将请求头和参数信息…...
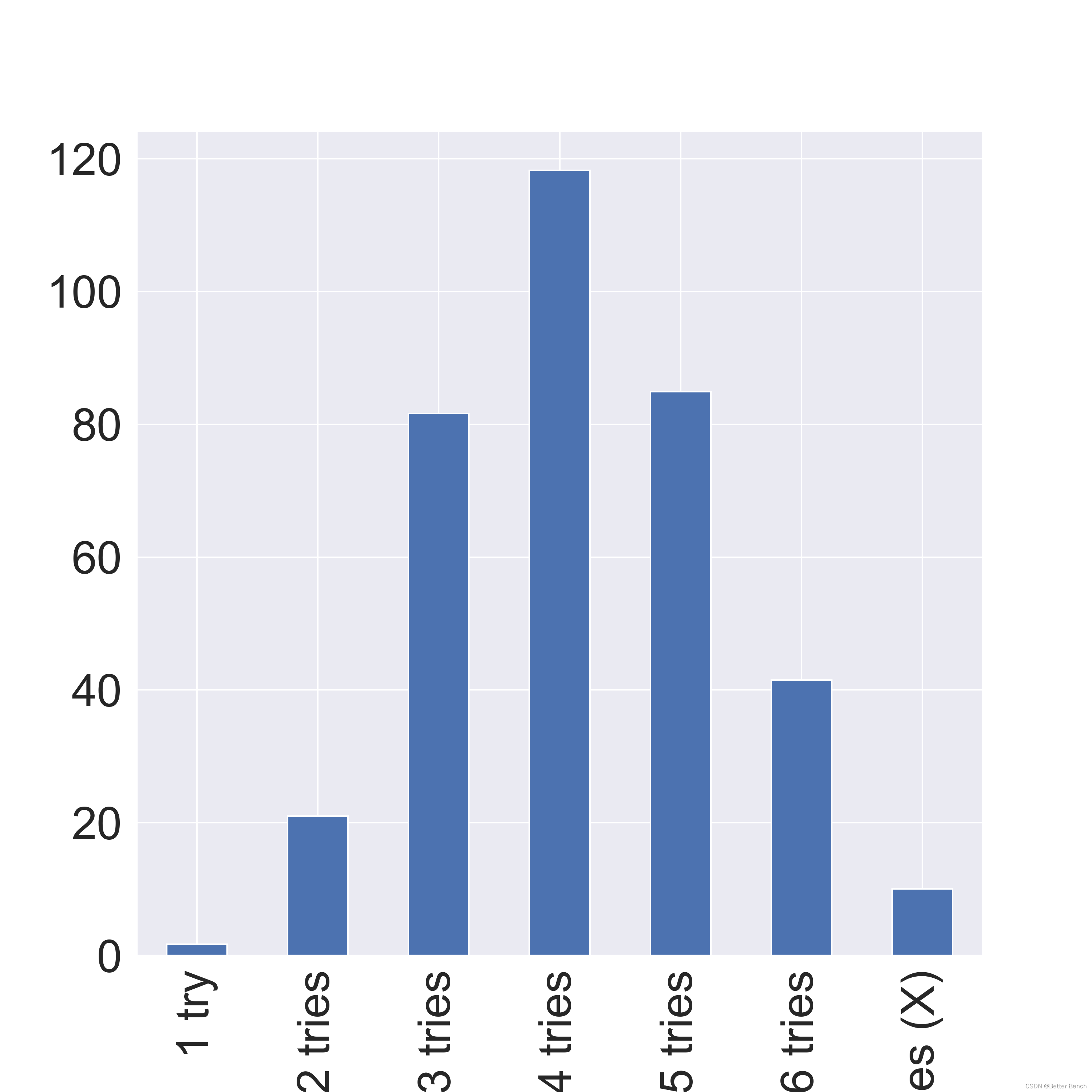
2023年美赛C题Wordle预测问题三、四建模及Python代码详细讲解
更新时间:2023-2-19 16:30 相关链接 (1)2023年美赛C题Wordle预测问题一建模及Python代码详细讲解 (2)2023年美赛C题Wordle预测问题二建模及Python代码详细讲解 (3)2023年美赛C题Wordle预测问题三、四建模…...
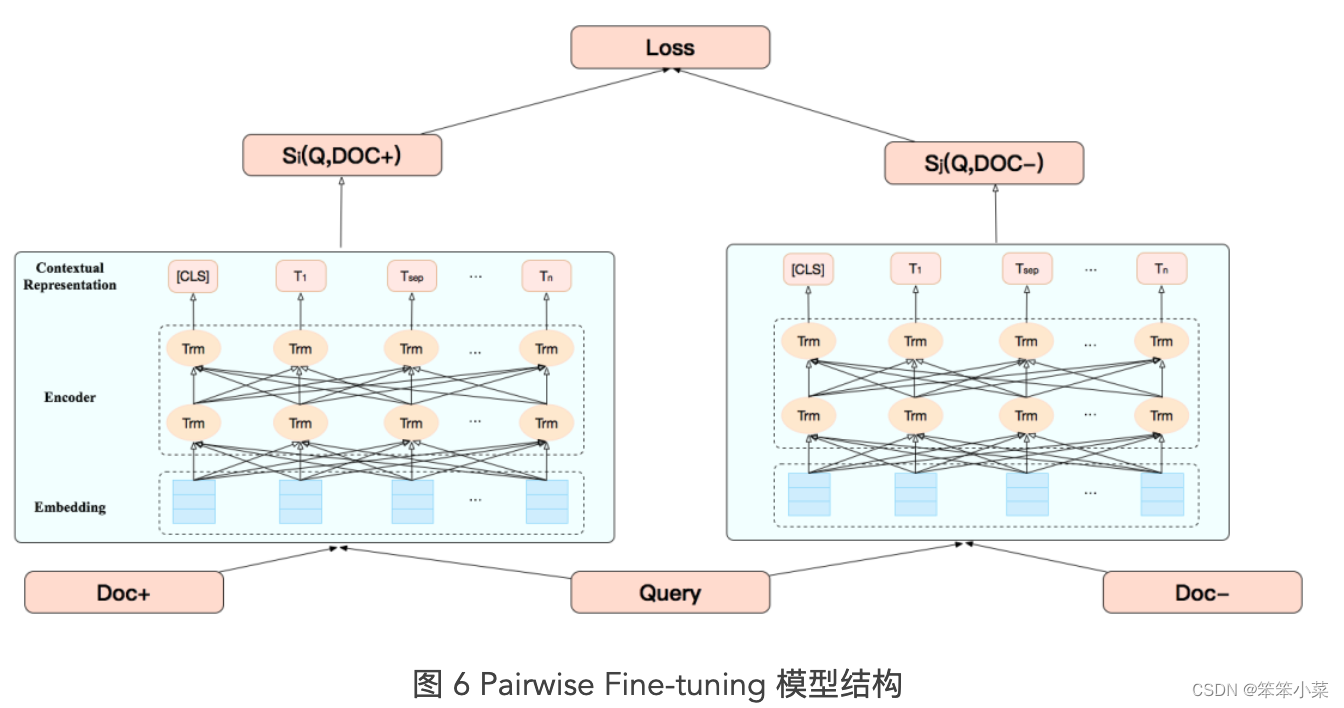
相关性-回忆录(持续更新)
1.TODO方向 (1)数据增强:finetuning阶段需要大量人工标注样本,消耗时间和成本。用户点击数据作为弱监督学习,可以尝试图网络构建节点和边(query聚合); 使用展现未点击生成对抗网络进…...
使用Python实现屏幕截图)
(必备技能)使用Python实现屏幕截图
(必备技能)使用Python实现屏幕截图 文章目录 (必备技能)使用Python实现屏幕截图 一、序言二、环境配置 1、下载pyautogui包2、下载opencv-python包3、下载PyQt5包4、下载pypiwin32包 三、屏幕截屏源码与解析 1、使用pyautogui方法实现截屏2、使用PyQt方法实现截屏 a.获取窗口…...

「数据仓库」怎么选择现代数据仓库?
构建自己的数据仓库时要考虑的基本因素我们用过很多数据仓库。当我们的客户问我们,对于他们成长中的公司来说,最好的数据仓库是什么时,我们会根据他们的具体需求来考虑答案。通常,他们需要几乎实时的数据,价格低廉&…...
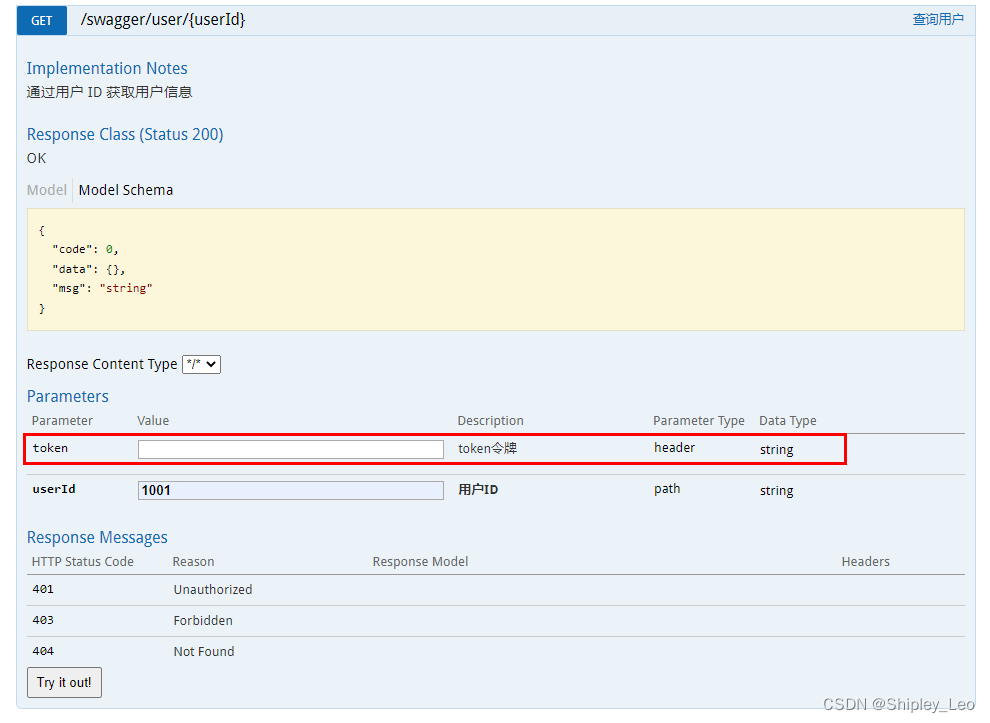
6.3 使用 Swagger 生成 Web API 文档
第6章 构建 RESTful 服务 6.1 RESTful 简介 6.2 构建 RESTful 应用接口 6.3 使用 Swagger 生成 Web API 文档 6.4 实战:实现 Web API 版本控制 6.3 使用 Swagger 生成 Web API 文档 高质量的 API 文档在系统开发的过程中非常重要。本节介绍什么是 Swaggerÿ…...
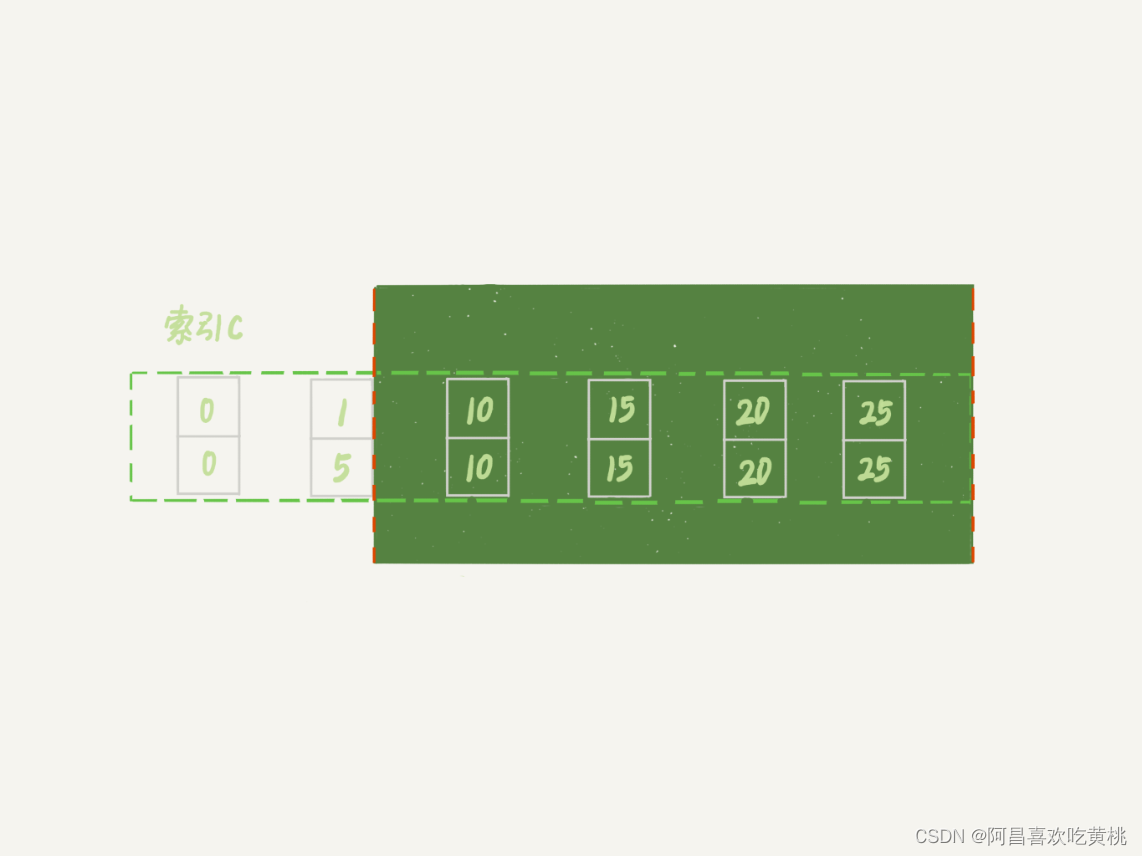
Day894.加锁规则的一些问题 -MySQL实战
加锁规则的一些问题 Hi,我是阿昌,今天学习记录的是关于加锁规则的一些问题的内容。 加锁规则,这个规则中,包含了两个“原则”、两个“优化”和一个“bug”: 原则 1:加锁的基本单位是 next-key lock。nex…...
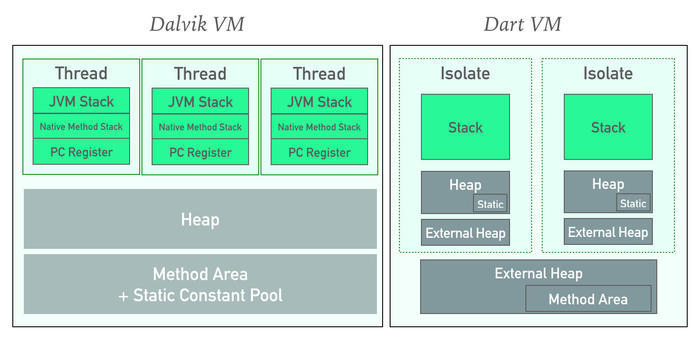
【Flutter入门到进阶】Dart进阶篇---Dart异步编程
1 并行与并发的编程区别 1.1 并发与并行 1.1.1 说明 我们举个例子,如果有条高速公路 A 上面并排有 8 条车道,那么最大的并行车辆就是 8 辆此条高速公路 A 同时并排行走的车辆小于等于 8 辆的时候,车辆就可以并行运行。 CPU 也是这个原理,一个 CPU 相当于一个高速公路 A,核心数…...

点云配准方法原理(NDT、ICP)
配准是点云处理中的一个基础问题,众多学者此问题进行了广泛而深入的研究,也出现了一系列优秀成熟的算法,在三维建模、自动驾驶等领域发挥着重要的作用。 本文主要介绍粗配准NDT (Normal Distribution Transform) 与 精配准ICP (Iterative Cl…...

大规模 IoT 边缘容器集群管理的几种架构-0-边缘容器及架构简介
📚️Reference: IoT 边缘计算系列文章 什么是边缘容器? 边缘容器的概念 边缘容器是分散的计算资源,尽可能靠近最终用户或设备,以减少延迟、节省带宽并增强整体数字体验。 可以访问互联网的设备数量每天都在增加。有包括但不限于…...
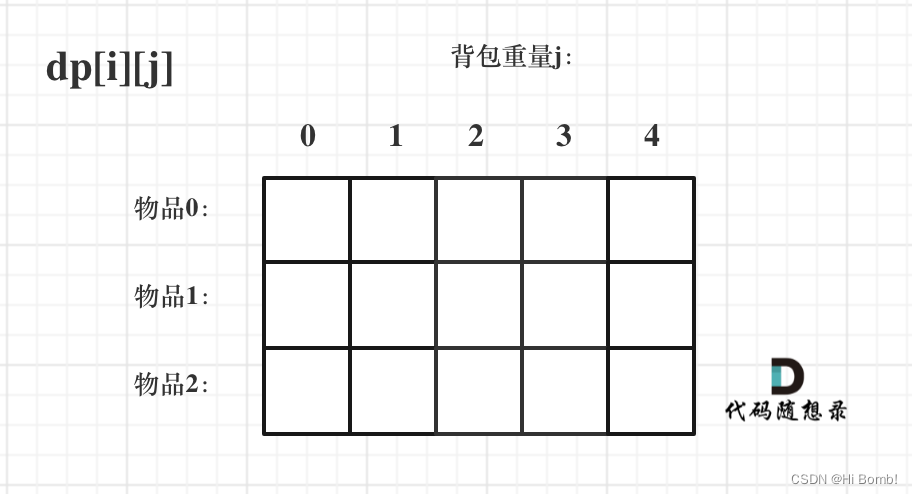
代码随想录算法训练营第45天动态规划 背包基础 1 2、 416. 分割等和子集
文章目录01背包基础 (二维数组)思路递推公式初始化遍历顺序一维dp数组(滚动数组)一维数组的递推公式遍历顺序LeetCode 416. 分割等和子集思路总结01背包基础 (二维数组) 思路 根据动态规划五部进行分析&a…...
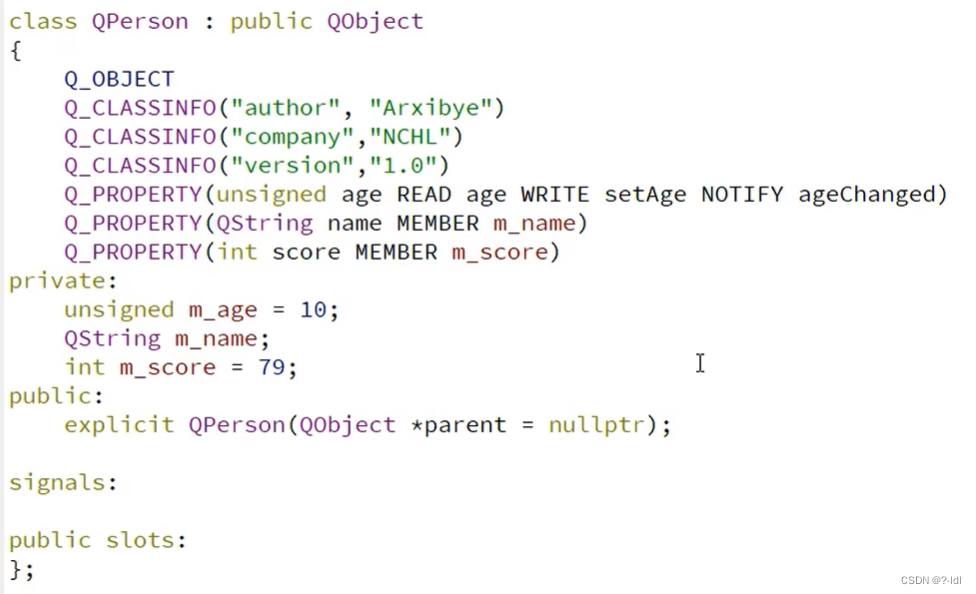
QT学习记录(六)类对象属性
类对象属性用来描述类对象的一些信息和当前的状态。类对象属性可以由类的编写者在编写类的时候定义,也可以由类的使用者在使用对象的时候定义。 由类的编写者定义 QPROPERTY()宏就是用来定义一个对象属性。 以第二行属性举例 QPROPERTY(bool enabled READ isEnabl…...

Spring Cloud Alibaba从搭建到源码完整进阶教程
微服务简介 Spring Cloud Alibaba 微服务简介 Nacos注册中心配置中心 Spring Cloud Nacos实战(一)- 下载和安装 Spring Cloud Nacos实战(二)- 服务提供者注册 Spring Cloud Nacos实战(三)- 服务消费者…...
Spring Cloud Nacos实战(一)- 下载和安装
Spring Cloud Alibaba Nacos下载和安装 Nacos介绍 Nacos(Naming Configuration Service) 是一个易于使用的动态服务发现、配置和服务管理平台,用于构建云原生应用程序 服务发现是微服务架构中的关键组件之一。Nacos 致力于帮助您发现…...
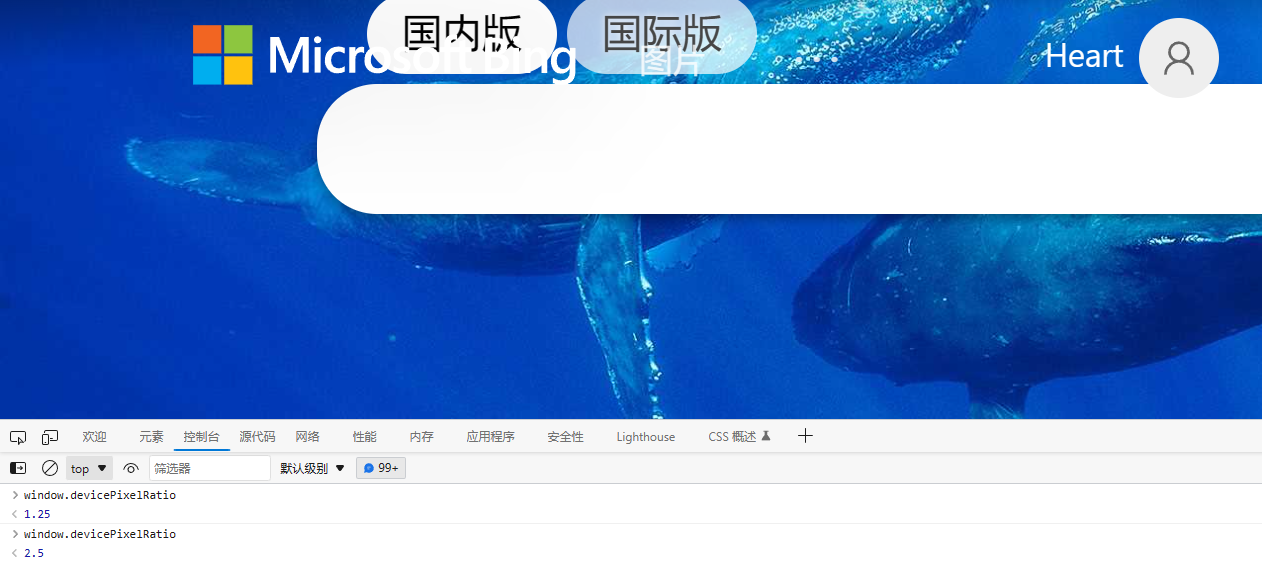
深入理解设备像素比
文章目录参考描述像素分辨率显示分辨率图像分辨率物理分辨率分辨率单位(仅部分)DPIPPI设备像素比设备物理像素设备独立像素设备像素比产生放大与缩小尾声参考 项目描述关于物理像素、逻辑像素(css像素)、分辨率、像素比的超详细讲…...
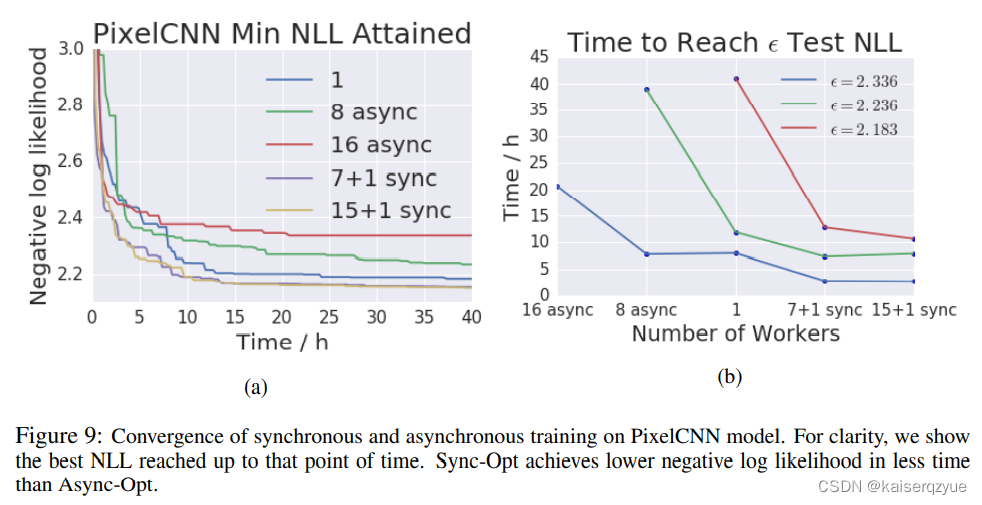
Revisiting Distributed Synchronous SGD 带有Back-up机制的分布式同步SGD方法 论文精读
论文链接:Revisiting Distributed Synchronous SGD ABS 本文介绍了用于分布式机器学习的同步和异步SGDSGDSGD,同时指出各自的缺点:stragglersstragglersstragglers和stalenessstalenessstaleness。 同时为了解决同步SGDSGDSGD存在straggle…...
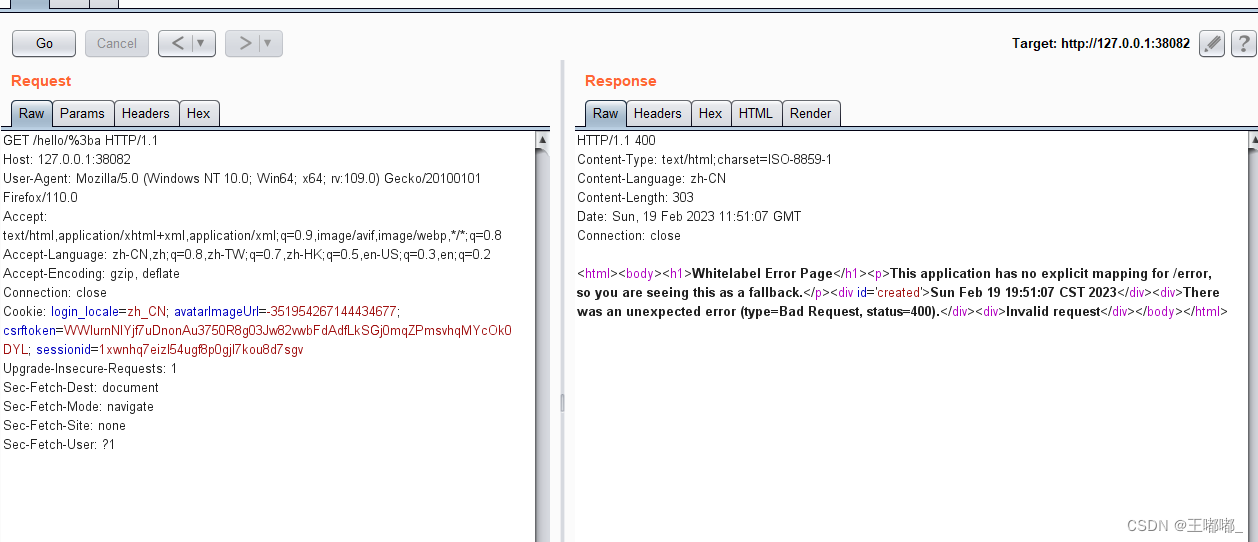
shiro CVE-2020-13933
0x00 前言 同CVE-2020-1957,补充一下笔记,在CVE-2020-1957的基础上进行了绕过。 影响版本:Apache Shiro < 1.6.0 环境搭建参考:shiro CVE-2020-1957 0x01 漏洞复现 CVE-2020-13933中使用%3b绕过了shiro /*的检测方式&…...

斐波那契数列(递归+迭代)
目录什么是斐波那契数列递归写法使用递归写法的缺点迭代写法(效率高)什么是斐波那契数列 斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多斐波那契(Leonardo Fibonacci)以兔子繁殖为例…...
2022黑马Redis跟学笔记.实战篇(六)
2022黑马Redis跟学笔记.实战篇 六4.7.达人探店功能4.7.1.分享探店图文1. 达人探店-发布探店笔记2. 达人探店-查看探店笔记4.7.2.点赞功能4.7.3.基于List实现点赞用户列表TOP104.7.4.基于SortedSet实现点赞排行榜4.8.关注列表4.8.1.关注列表实现原理4.8.2.添加关注1. 好友关注-关…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...
