day47【代码随想录】动态规划之买卖股票的最佳时机III、买卖股票的最佳时机IV、最佳买卖股票时机含冷冻期、买卖股票的最佳时机含手续费
文章目录
- 前言
- 一、买卖股票的最佳时机III(力扣123)
- 二、买卖股票的最佳时机IV(力扣188)
- 三、最佳买卖股票时机含冷冻期(力扣309)
- 四、买卖股票的最佳时机含手续费(力扣714)
- 股票买卖问题总结
前言
1、买卖股票的最佳时机III
2、买卖股票的最佳时机IV
3、最佳买卖股票时机含冷冻期
4、买卖股票的最佳时机含手续费
一、买卖股票的最佳时机III(力扣123)
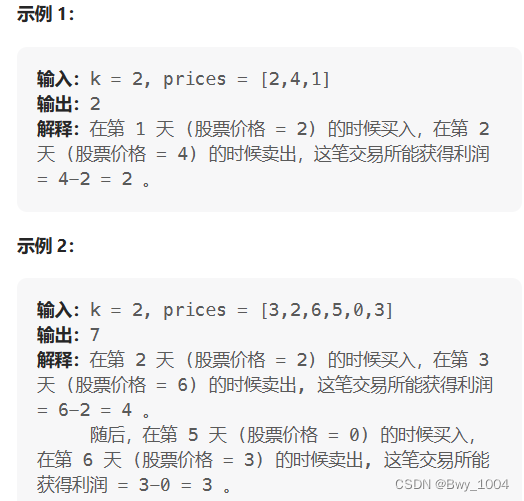
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
8888
分析:
与之前的区别在于最多可以买卖两次
动规五部曲
1、dp[]数组以及下标含义
dp[i][0]:不操作
dp[i][1]:第一次持有
dp[i][2]:第一次不持有
dp[i][3]:第二次持有
dp[i][4]:第二次不持有
2、递推公式
dp[i][0] = dp[i-1][0]
dp[i][1] = Math.max(dp[i-1][1],-price[i])
dp[i][2] = Math.max(dp[i-1][2],dp[i-1][1]+price[i])
dp[i][3] = Math.max(dp[i-1][3],dp[i-1][2]-price[i])
dp[i][4] = Math.max(dp[i-1][4],dp[i-1][3]+price[i])
3、初始化
dp[0][0] = 0;
dp[0][1] = -price[0];
dp[0][2] = 0;
dp[0][3] = -price[0];
dp[0][4] = 0;
4、遍历顺序
从前向后遍历,因为dp[i],依靠dp[i - 1]的数值。
二维dp数组
class Solution {public int maxProfit(int[] prices) {int[][] dp = new int[prices.length][5];dp[0][0] = 0;dp[0][1] = -prices[0];dp[0][2] = 0;dp[0][3] = -prices[0];dp[0][4] = 0;for(int i=1;i<prices.length;i++){dp[i][1] = Math.max(dp[i-1][1],-prices[i]);dp[i][2] = Math.max(dp[i-1][2],dp[i-1][1]+prices[i]);dp[i][3] = Math.max(dp[i-1][3],dp[i-1][2]-prices[i]);dp[i][4] = Math.max(dp[i-1][4],dp[i-1][3]+prices[i]);}return dp[prices.length-1][4];}
}
优化版:(滚动数组):
class Solution {public int maxProfit(int[] prices) {int[] dp = new int[5];dp[0] = 0;dp[1] = -prices[0];dp[2] = 0;dp[3] = -prices[0];dp[4] = 0;for(int i=1;i<prices.length;i++){dp[1] = Math.max(dp[1],-prices[i]);dp[2] = Math.max(dp[2],dp[1]+prices[i]);dp[3] = Math.max(dp[3],dp[2]-prices[i]);dp[4] = Math.max(dp[4],dp[3]+prices[i]);}return dp[4];}
}
二、买卖股票的最佳时机IV(力扣188)
给定一个整数数组 prices ,它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
分析:
与之前的区别在于最多可以买卖k次
根据上一题所表现出来的规律:
1、dp[]数组以及下标含义
dp[i][0]:不操作
dp[i][1]:第一次持有
dp[i][2]:第一次不持有
dp[i][3]:第二次持有
dp[i][4]:第二次不持有
……
当有k次买卖时,奇数表示买入,偶数表示卖出。
初始化
for(int j=0;j<2*k+1;j++){if(j%2==1){dp[0][j] = -prices[0];}
}
递推公式
dp[i][0] = dp[i-1][0]
dp[i][1] = Math.max(dp[i-1][1],-price[i])
dp[i][2] = Math.max(dp[i-1][2],dp[i-1][1]+price[i])
dp[i][3] = Math.max(dp[i-1][3],dp[i-1][2]-price[i])
dp[i][4] = Math.max(dp[i-1][4],dp[i-1][3]+price[i])
for(int i = 1; i<prices.length; i++){for(int j=1; j<2*k+1;j=j+2){dp[i][j] = Math.max(dp[i-1][j],dp[i-1][j-1]-prices[i]);dp[i][j+1] = Math.max(dp[i-1][j+1],dp[i-1][j]+prices[i]);}
}
class Solution {public int maxProfit(int k, int[] prices) {int[][] dp = new int[prices.length][2*k+1];for(int j=1;j<2*k+1;j++){if(j%2==1) dp[0][j] = -prices[0];}for(int i=1;i<prices.length;i++){for(int j=0;j<2*k-1;j=j+2){dp[i][j+1] = Math.max(dp[i-1][j+1],dp[i-1][j]-prices[i]);dp[i][j+2] = Math.max(dp[i-1][j+2],dp[i-1][j+1]+prices[i]);}}return dp[prices.length-1][2*k];}
}

三、最佳买卖股票时机含冷冻期(力扣309)
给定一个整数数组,其中第 i 个元素代表了第 i 天的股票价格 。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。

动规五部曲:
1、dp[]数组以及下标含义
dp[i][0]:持有股票的状态
dp[i][1]:保持卖出股票的状态
dp[i][2]:卖出股票状态
dp[i][3]:冷冻期
为什么要把 不持有股票状态拆分为两个部分【保持卖出股票的状态、卖出股票状态】,因为有冷冻期。必须前一天是卖出股票的状态,那么下一天才能是冷冻期
2、递推公式
持有股票状态:
1、i-1天就持有:dp[i][0] = dp[i-1][0];
2、冷冻期之后买入股票:dp[i][0] = dp[i-1][3] - prices[i];
3、冷冻期之后一直没有操作,一直都是保持卖出股票状态,直到第i天买入:dp[i][0] = dp[i-1][1] - prices[i];
因此:dp[i][0] = Math.max(dp[i-1][0], dp[i-1][3] - prices[i], dp[i][0] = dp[i-1][1] - prices[i])
保持卖出股票状态:
1、前一天就是保持卖出股票的状态:dp[i][1] = dp[i-1][1];
2、前一天是冷冻期,dp[i][1] = dp[i-1][3]
因此:dp[i][1] = Math.max(dp[i-1][1] , dp[i-1][3])
卖出股票状态:
1、前i-1天持有股票状态,第i天卖出股票.dp[i][2] = dp[i-1][0]+prices[i];
因此:dp[i][2]=dp[i-1][0]+prices[i];
冷冻期状态
1、前一天卖出股票状态,第i天就是冷冻期 dp[i][3] = dp[i-1][2]
因此:dp[i][3] = dp[i-1][2];
3、初始化
dp[0][0] = -prices[0];
dp[0][1] 在dp[i][0] = Math.max(dp[i-1][0], dp[i-1][3] - prices[i], dp[i][0] = dp[i-1][1] - prices[i]) 这个状态下会用到,假设i=1带入之后:
dp[1][0] = max(dp[0][0],dp[0][3]-prices[1], dp[0][1]-prices[1]);
dp[0][1] = 0;
dp[0][2] = 0;
dp[0][3] = 0;
4、遍历顺序
从前向后遍历,因为dp[i],依靠dp[i - 1]的数值。
class Solution {public int maxProfit(int[] prices) {int[][] dp = new int[prices.length][4];//初始化dp[0][0] = -prices[0];dp[0][1] = 0;dp[0][2] = 0;dp[0][3] = 0;//遍历for(int i=1;i<prices.length;i++){//持有股票的状态dp[i][0] = Math.max(Math.max(dp[i-1][0],dp[i-1][1]-prices[i]),dp[i-1][3]-prices[i]);//保持卖出股票的状态dp[i][1] = Math.max(dp[i-1][1],dp[i-1][3]);//卖出股票状态dp[i][2] = dp[i-1][0]+prices[i];//冷冻期dp[i][3] = dp[i-1][2];}return Math.max(Math.max(dp[prices.length-1][3],dp[prices.length-1][2]),dp[prices.length-1][1]);}
}

四、买卖股票的最佳时机含手续费(力扣714)
给定一个整数数组 prices,其中 prices[i]表示第 i 天的股票价格 ;整数 fee 代表了交易股票的手续费用。
你可以无限次地完成交易,但是你每笔交易都需要付手续费。如果你已经购买了一个股票,在卖出它之前你就不能再继续购买股票了。
返回获得利润的最大值。
注意:这里的一笔交易指买入持有并卖出股票的整个过程,每笔交易你只需要为支付一次手续费。

在之前有用贪心算法进行求解:
贪心算法求解
分析:
买卖股票的最佳时机II 可以进行多次买卖,但多了手续费
dp[i][0]:表示第i天持有股票所得现金。
dp[i][1]:表示第i天不持有股票所得最多现金
dp[i][0] = max(dp[i-1][0],dp[i-1][1]-prices[i]-fee)
dp[i][1] = max(dp[i-1][1],dp[i-1][0]+prices[i]);
class Solution {public int maxProfit(int[] prices, int fee) {int[][] dp = new int[prices.length][2];dp[0][0] = -prices[0]-fee;for(int i=1;i<prices.length;i++){dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1]-prices[i]-fee);dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0]+prices[i]);}return dp[prices.length-1][1];}
}
优化后(一维滚动数组)
class Solution {public int maxProfit(int[] prices, int fee) {int[] dp = new int[2];dp[0] = -prices[0]-fee;for(int i=1;i<prices.length;i++){dp[0] = Math.max(dp[0],dp[1]-prices[i]-fee);dp[1] = Math.max(dp[1],dp[0]+prices[i]);}return dp[1];}
}

股票买卖问题总结
买卖股票的最佳时机(力扣121) 只能买卖一次
dp[i][0]:持有股票的状态
dp[i][1]:不持有股票的状态
dp[0][0] = -prices[0];
dp[0][1] = 0;
dp[i][0] = max(dp[i-1][0], -prices[i])
dp[i][1] = max(dp[i-1][1] , dp[i-1][0]+prices[i])
买卖股票的最佳时机||(力扣122)可以买卖多次
dp[i][0]:持有股票的状态
dp[i][1]:不持有股票的状态
dp[0][0] = -prices[0];
dp[0][1] = 0;
dp[i][0] = max(dp[i-1][0], dp[i-1][1]-prices[i])
dp[i][1] = max(dp[i-1][1] , dp[i-1][0]+prices[i])
细微变化在于持有股票状态的递推过程
买卖股票的最佳时机|||(力扣123)最多买卖2次
dp[i][0] 不操作
dp[i][1]:第一次持有股票状态
dp[i][2]:第一次不持有股票状态
dp[i][3]:第二次持有股票状态
dp[i][4]:第二次不持有股票状态
初始化
dp[0][0]= 0
dp[0][1] = -prices[0];
dp[0][2] = 0;
dp[0][3] = -prices[0];
dp[i][0] = dp[i-1][0]
dp[i][1] = max(dp[i-1][1],-prices[i])
dp[i][2] = max(dp[i-1][2], dp[i-1][1]+prices[i])
dp[i][3] = max(dp[i-1][3], dp[i-1][2]-prices[i])
dp[i][4] = max(dp[i-1][4], dp[i-1][3]+prices[i])
买卖股票的最佳时机IV(力扣188) 最多买卖k次
dp[i][0] 不操作
dp[i][1]:第一次持有股票状态
dp[i][2]:第一次不持有股票状态
dp[i][3]:第二次持有股票状态
dp[i][4]:第二次不持有股票状态
……
0 ----- 2*k
奇数是持有股票状态
偶数是卖出股票状态
初始化时:
if(j%2==1) dp[0][j] = -prices[0];
奇数时:dp[i][j] = max(dp[i-1][j],dp[i-1][j-1] - prices[i])
偶数时:dp[i][j+1] = max(dp[i-1][j+1], dp[i-1][j] +prices[i])
最佳买卖股票时机含冷冻期(力扣309) 买卖多次,卖出后有一天是冷冻期
dp[i][0]:持有股票的状态
dp[i][1]:保持卖出股票的状态
dp[i][2]:卖出股票的状态
dp[i][3]:冷冻期
初始化
dp[0][0] = -prices[0];
dp[i][0] = max(dp[i-1][0], dp[i-1][1]-prices[i], dp[i-1][3]- prices[i])
dp[i][1] = max(dp[i-1][1], dp[]i-1[3])
dp[i][2] = dp[i-1][0]+prices[i]
dp[i][3] = dp[i-1][2]
买卖股票的最佳时机含手续费(力扣714)买卖多次,每次都有手续费
dp[i][0]:持有股票的状态
dp[i][1]:不持有股票的状态
dp[0][0] = -prices[0]-fee;
dp[0][1] = 0;
dp[i][0] = max(dp[i-1][0], dp[i-1][1]-prices[i]-fee)
dp[i][1] = max(dp[i-1][1] , dp[i-1][0]+prices[i])
细微变化在于多减去手续费
相关文章:

day47【代码随想录】动态规划之买卖股票的最佳时机III、买卖股票的最佳时机IV、最佳买卖股票时机含冷冻期、买卖股票的最佳时机含手续费
文章目录前言一、买卖股票的最佳时机III(力扣123)二、买卖股票的最佳时机IV(力扣188)三、最佳买卖股票时机含冷冻期(力扣309)四、买卖股票的最佳时机含手续费(力扣714)股票买卖问题总…...
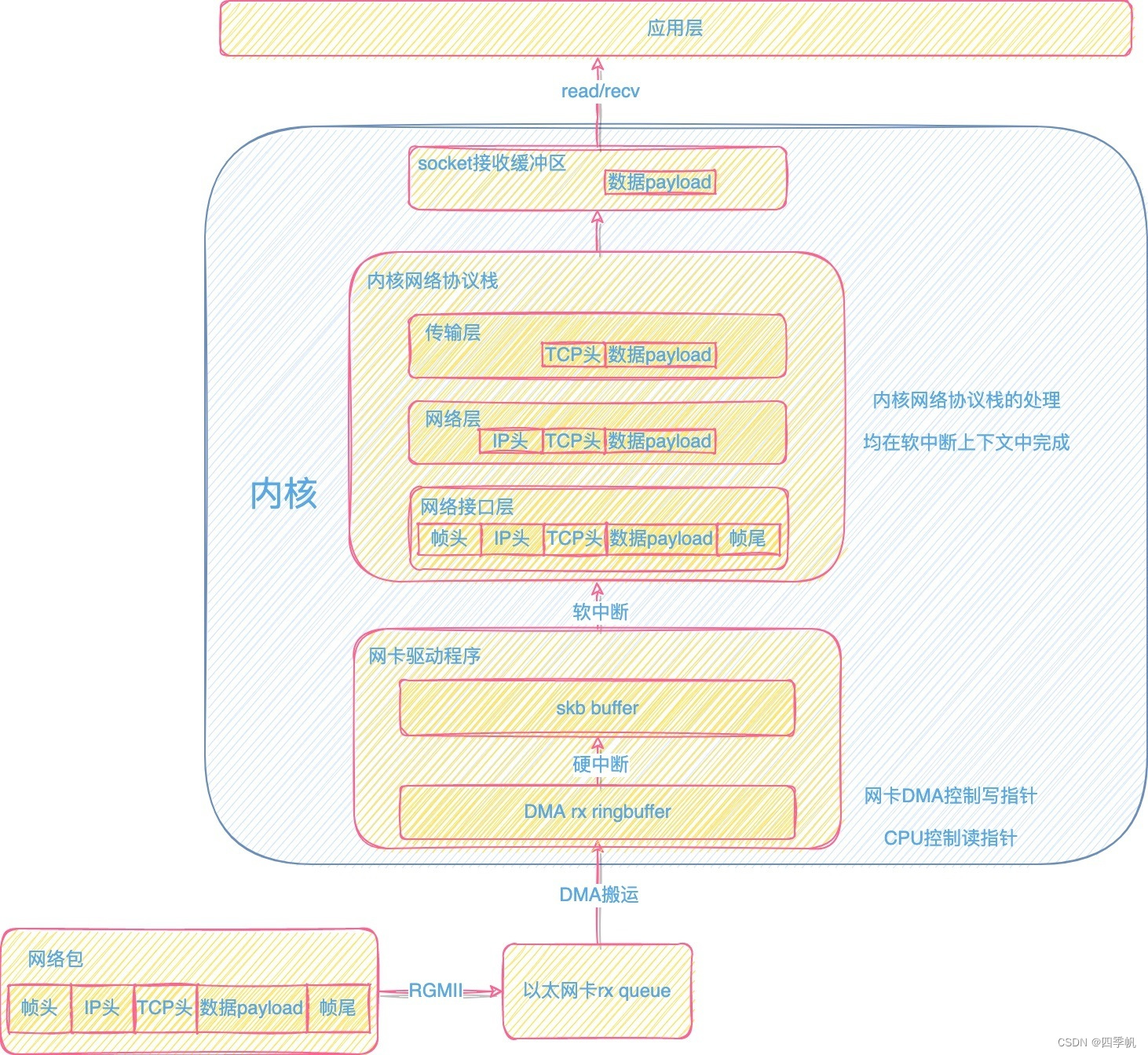
网络数据包接收流程
1. 网络数据包接收流程简述 典型的以太网卡网络包接收流程如下: 1.网络包通过物理介质传到接收端的phy芯片; 2.phy芯片通过RGMII协议传到MAC芯片rx queue fifo中; 3.MAC芯片通过专用DMA将网络包搬运到网卡驱动程序预先分配好的rx ringbuffer中…...
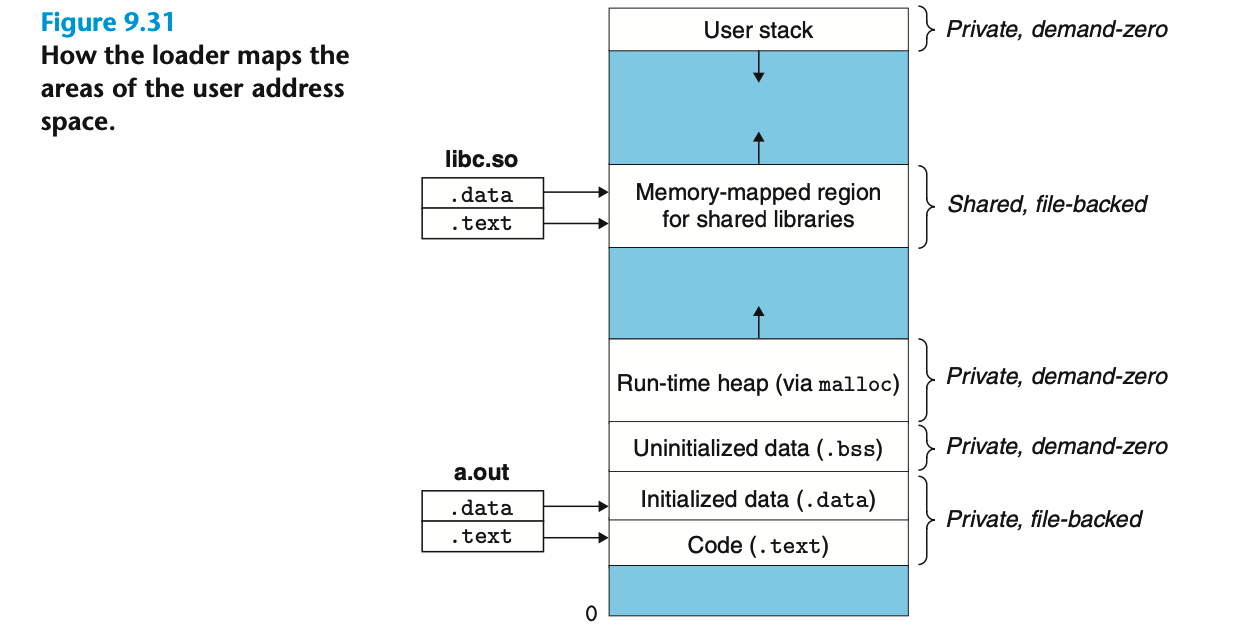
CSAPP学习笔记——虚拟内存(二)
案例研究 Intel Core i7 该处理底层的Haswell微体系结构允许64位的虚拟和物理地址空间,而现在的Core i7实现支持48位(256TB)虚拟地址空间和52位(4PB)物理地址空间,这对目前来说已经完全够用了。ÿ…...

面试sql
创建表 create table Student ( Sno varchar(20) primary key,Sname varchar(20) UNIQUE,Ssex varchar(2),Sbirthday date,class varchar(20) )create table Course ( Cno varchar(20) primary key,Cname varchar(20) UNIQUE,Tno varchar(20) )create table Score ( …...

Python编程自动化办公案例(2)
作者简介:一名在校计算机学生、每天分享Python的学习经验、和学习笔记。 座右铭:低头赶路,敬事如仪 个人主页:网络豆的主页 目录 前言 一.前期代码 二.实现批量读取 1.os库 2.实现思路 (1&#…...
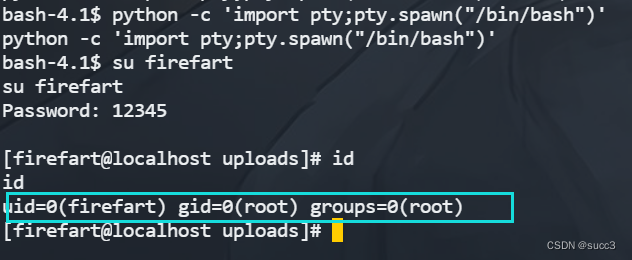
Vulnhub 渗透练习(七)—— FRISTILEAKS: 1.3
环境搭建 下载链接 virtualbox 打开靶机设置为 host-only,攻击机同样。 具体可点此处 信息收集 开了个 80 端口。 用的是 apache 2.2.15 ,这个版本有个解析漏洞。 目录 根据首页的图片猜测 /fristi/ 目录(不过我没想到 -_-&#x…...
阶段二10_面向对象高级_分类分包思想和案例环境搭建
一.分类思想 1.分类思想概念: 分工协作,专人干专事 2.信息管理系统分类[案例] Student 类-------------------->标准学生类,封装键盘录入的学生信息(id , name , age , birthday) StudentDao 类-----------------&…...

关于打印工具print-js的使用
https://www.jianshu.com/p/f6f09dd9f7db第一步 安装组件//安装print-js npm install print-js --save //删除print-js npm uninstall print-js //安装固定版本 npm install print-js版本号 --save // 全局安装 npm install print-js --save -g第二步 引入组件安装成功后&#…...

Doxygen使用
文章目录简介Doxygen的安装Doxygen的配置生成配置文件常用配置Doxygen注释头文件注释:函数的注释:Doxygen文档生成reference简介 Doxygen 是一个流行的用于生产代码文档的工具,关于它的介绍可以参考官网:https://www.doxygen.nl/index.html。 我使用Dox…...

MySQL数据库调优————表结构设计优化
三范式 第一范式 字段具有原子性,即数据库表的每一个字段都是不可分割的原子数据项,不能是集合、数组、记录等非原子数据项当实体中的每个属性有多个值时,必须拆分为不同的属性 第二范式 满足第一范式的基础上,要求每一行数据…...

set对象和map对象
1 Set对象 介绍: Set数据结构类似数组,但所有成员的值唯一。 Set本身为一个构造函数,用来生成 Set数据结构,使用 add方法来添加新成员。 let a new Set(); [1,2,2,1,3,4,5,4,5].forEach(x>a.add(x)); for(let k of a){ console.log(k…...
流的使用)
stream()流的使用
文章目录引入流流的操作中间操作终端操作流的使用谓词筛选筛选各异的元素流的切片截断流跳过元素映射流的扁平化查找和匹配归约元素求和、最大值和最小值数值流构建流由值构建流由数组创建流引入流 java api提供的一种利用声明式的方式处理数据集合的一个东西,可以…...

C++学习笔记-常量
在程序执行过程中,其值不能改变的量称为常量(Constant)。普通常量的类型是根据数据的书写形式来决定的。如 100 是整型常量,0.5 是实型常量,‘q’ 是字符型常量,“qianfeng” 是字符串常量。 常量是固定值,在程序执行期…...

JavaScript系列之实现继承的几种方式
文章の目录一、借助父构造函数继承属性1、实现方式2、优点3、缺点二、原型链继承1、实现方式2、优点3、缺点三、组合继承四、ES6继承的实现方式参考写在最后一、借助父构造函数继承属性 1、实现方式 先定义一个父构造函数(this指向为window);再定义一个子构造函数…...

java面试准备
1.自我介绍: 2.基础 : 1.集合 : java容器中分为collection 和map两大类 collection 分为list集合(有序且重复的),set集合(无序,不可重复) list集合分为arrayList集合 : 查询快,增删慢,它是基于数组结构的,对数据的增删是在数组的尾部进行添加或删除的,其效率相对于LinkedList…...
kafka-6-python单线程操作kafka
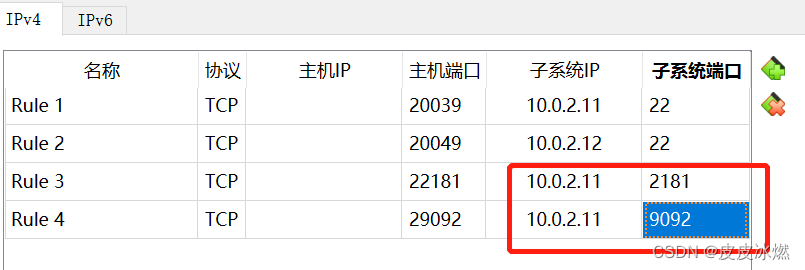
使用Python操作Kafka:KafkaProducer、KafkaConsumer Python kafka-python API的帮助文档 1 kafka tools连接 (1)/usr/local/kafka_2.13-3.4.0/config/server.properties listeners PLAINTEXT://myubuntu:9092 advertised.listenersPLAINTEXT://192.168.1.8:2909…...
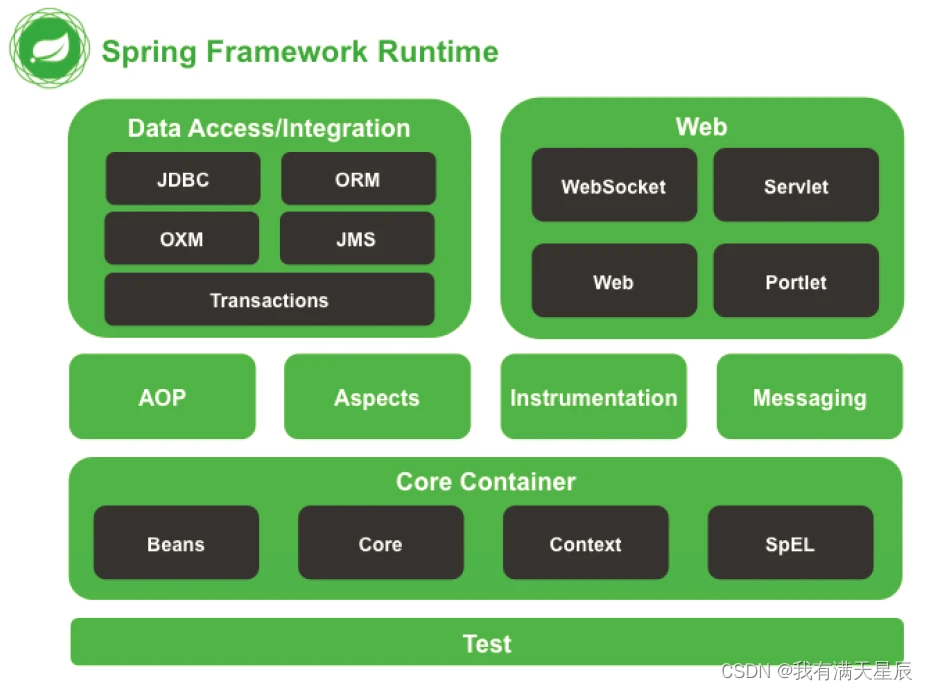
【Spring教程】1.Spring概述
1、概述 1.1、Spring是什么? Spring 是一款主流的 Java EE 轻量级开源框架 ,Spring 由“Spring 之父”Rod Johnson 提出并创立,其目的是用于简化 Java 企业级应用的开发难度和开发周期。Spring的用途不仅限于服务器端的开发。从简单性、可测…...

设计模式-代理模式
控制和管理访问 玩过扮白脸,扮黑脸的游戏吗?你是一个白脸,提供很好且很友善的服务,但是你不希望每个人都叫你做事,所以找了黑脸控制对你的访问。这就是代理要做的:控制和管理对象。 监视器编码 需求&…...
)
DPDK — MALLOC(librte_malloc,Memory Manager,内存管理组件)
目录 文章目录 目录MALLOC(librte_malloc,Memory Manager,内存管理组件)rte_malloc() 接口malloc_heap 结构体malloc_elem 结构体内存初始化流程内存申请流程内存释放流程MALLOC(librte_malloc,Memory Manager,内存管理组件) MALLOC 库基于 hugetlbfs 内核文件系统来实…...

【Java开发】Spring 12 :Spring IOC控制反转和依赖注入(解决单接口多实现类调用)
IOC 是 Inversion of Control 的简写,译为“控制反转”,Spring 通过 IOC 容器来管理所有 Java 对象的实例化和初始化,控制对象与对象之间的依赖关系。我们将由 IOC 容器管理的 Java 对象称为 Spring Bean,它与使用关键字 new 创建…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...

【java】【服务器】线程上下文丢失 是指什么
目录 ■前言 ■正文开始 线程上下文的核心组成部分 为什么会出现上下文丢失? 直观示例说明 为什么上下文如此重要? 解决上下文丢失的关键 总结 ■如果我想在servlet中使用线程,代码应该如何实现 推荐方案:使用 ManagedE…...

Yii2项目自动向GitLab上报Bug
Yii2 项目自动上报Bug 原理 yii2在程序报错时, 会执行指定action, 通过重写ErrorAction, 实现Bug自动提交至GitLab的issue 步骤 配置SiteController中的actions方法 public function actions(){return [error > [class > app\helpers\web\ErrorAction,],];}重写Error…...
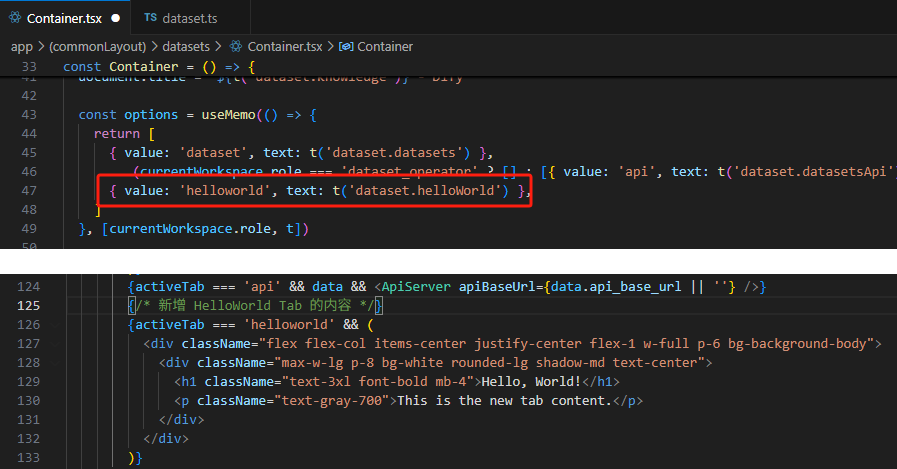
【技巧】dify前端源代码修改第一弹-增加tab页
回到目录 【技巧】dify前端源代码修改第一弹-增加tab页 尝试修改dify的前端源代码,在知识库增加一个tab页"HELLO WORLD",完成后的效果如下 [gif01] 1. 前端代码进入调试模式 参考 【部署】win10的wsl环境下启动dify的web前端服务 启动调试…...

PostgreSQL 与 SQL 基础:为 Fast API 打下数据基础
在构建任何动态、数据驱动的Web API时,一个稳定高效的数据存储方案是不可或缺的。对于使用Python FastAPI的开发者来说,深入理解关系型数据库的工作原理、掌握SQL这门与数据库“对话”的语言,以及学会如何在Python中操作数据库,是…...

Github 2025-06-07 Rust开源项目日报Top10
根据Github Trendings的统计,今日(2025-06-07统计)共有10个项目上榜。根据开发语言中项目的数量,汇总情况如下: 开发语言项目数量Rust项目10Dart项目1TypeScript项目1RustDesk: 用Rust编写的开源远程桌面软件 创建周期:1218 天开发语言:Rust, Dart协议类型:GNU Affero Ge…...
