【马蹄集】第二十三周——进位制专题
进位制专题
目录
- MT2186 二进制?不同!
- MT2187 excel的烦恼
- MT2188 单条件和
- MT2189 三进制计算机1
- MT2190 三进制计算机2
MT2186 二进制?不同!
难度:黄金 时间限制:1秒 占用内存:128M
题目描述
小码哥是一个对数很敏感的人,即使给他很多个很像的数串,他都能找出没有出现过的数串。
或许是有些无聊,小码哥给你一个字符串数组 nums,里面包含 n n n 个二进制字符串(长度都为 n n n ),现请你找出不在数组中的二进制字符串。若有多解,返回对应十进制最小的一个。格式
输入格式:一行二进制字符串数组,字符串之间以空格分割;
输出格式:一个不在数组中的二进制字符串。样例 1
输入:01 10
输出:00
备注
其中: 1 ≤ n ≤ 16 1 \le n \le 16 1≤n≤16,nums中所有字符互不相同。
相关知识点:
进位制
题解
本题要求找出尚未在输入数据中出现的最小值(所有数据的最小取值为 0)。但是题目给出的数据为二进制字符串(合法的),因此为了找出最小未出现的数,我们需要先将所有输入的二进制字符串转换为十进制数,并将这些数存放进一个集合 nums 中。接下来,从 0 开始逐步向后枚举整数,一旦存在某个数不在集合 nums 中,就说明这个数是尚未在输入数据中出现的最小数。注意:我们还需对这个数进行格式转换!即将这个数由十进制再转换为二进制字符串(长度需要和输入数据的长度一致)。
下面直接给出求解此题的完整代码(已 AC):
/*MT2186 二进制?不同! 测试数据:001 100 000
*/
#include<bits/stdc++.h>
using namespace std;set<int> nums;// 该函数将(合法的)二进制数字串转换为十进制数字
int getDecFromBin(string str)
{int sum = 0, base = 1;for(int i=str.size()-1; i>=0; i--){sum += base*(str[i]-'0');base *= 2;}return sum;
} // 将一个十进制数转换为指定长度的二进制字符串
string toBinary(int n, int len)
{string str = "";while(len--){if(n&1) str = "1"+str;else str = "0"+str;n >>= 1;}return str;
} int main( )
{// 输入数据string str;while(cin>>str)nums.insert(getDecFromBin(str));// 记录当前输入二进制字符串的长度int binStrlen = str.length();// 寻找最小值,并在进行格式转换后输出 for(int i=0; ; i++){// 找到一个尚未在集合中出现的最小数值if(nums.find(i) == nums.end()){cout<<toBinary(i, binStrlen)<<endl;break;}}return 0;
}
MT2187 excel的烦恼
难度:钻石 时间限制:2秒 占用内存:128M
题目描述
你用过 Excel 么?
在 excel 中,第一列被标为 A,第二列为 B,以此类推,第 26 列为 Z。接下来为由两个字母构成的列号:第 27 列为 AA,第 28 列为 AB……在标为 ZZ 的列之后则由三个字母构成列号,如此类推。
行号为从 1 开始的整数。
单元格的坐标由列号和行号连接而成。比如,BC23 表示位于第 55 列 23 行的单元格。
有时也会采用被称为 RXCY 的坐标系统,其中 X 与 Y 为整数,坐标 (X, Y) 直接描述了对应单元格的位置。比如,R23C55 即为前面所述的单元格。
小码哥请你编写一个程序,将所给的单元格坐标转换为另一种坐标系统下面的形式。格式
输入格式:第一行一个整数 T(1≤T≤10^5) 表示将有 T 次询问;
接下来 T 行,每行一个坐标。
输出格式:输出 T 行,每行一个被转换的坐标。样例 1
输入:3
R12C3
AE32
BB11输出:C12
R32C31
R11C54备注
每个坐标都是正确的。保证输入输出数据均在int范围内。输入输出数据字母部分均为大写。
相关知识点:
进位制
题解
这道题表面是在对两种坐标形式进行转换,但实际上也是在考察进制转换。例如,对于 excel 形式的坐标,其列号 BC 对应在十进制中为 55( 2 × 2 6 1 + 3 × 2 6 0 = 55 2×26^1+3×26^0=55 2×261+3×260=55),所以题中将 BC23 解析为第 55 行第 23 列的单元格。因此,这里的进制转换问题实际上是十进制与以 A − Z A-Z A−Z 表达的二十六进制数之间的互相转换。
对于本题,由于输入数据并没有说明其具体是哪一种形式的坐标表达,因此我们需要做的第一件事是识别坐标格式。观察两种形式的坐标不难发现,excel 形式的坐标是 “字母+数字”,而 RXCY 形式的坐标是 “字母+数字+字母+数字”,这两种形式的本质区别在于:RXCY 的格式中,会在数字的后面出现字母;而 excel 形式下,数字后面不可能出现字母。因此可以根据这一本质区别进行格式识别,并在后续进行格式转换。
当完成了对输入坐标字符串的格式检测后,便能分别进行格式转换了。具体的转换过程并不难(详细细节可看这之后的例题:MT2189 三进制计算机1、MT2190 三进制计算机2),下面直接给出求解本题的完整代码(已 AC):
/*MT2187 excel的烦恼
*/
#include<bits/stdc++.h>
using namespace std;string str;
int T;
char apt[] = " ABCDEFGHIJKLMNOPQRSTUVWXYZ";// 检测当前的坐标字符串属于那种格式:
// 0 EXCEL 格式
// 1 RXCY 格式
bool getFormat(string str)
{bool flag = 0;int strlen = str.length();for(int i=0; i<strlen; i++) {// 数字出现标记 if(isdigit(str[i]))flag = true;// 检测是否为 RXCY 模式if(flag && str[i]=='C')return true;}return false;
} // 格式转换
void transform(string str)
{// 格式识别bool mode = getFormat(str);// 格式转换 int row = 0, col = 0, len = str.length();if(mode){ // mode 1:RXCY 转 ECXCEL 格式 // 定位 R 与 C 所在位置 int R = str.find("R"), C = str.find("C");// 取出行号和列号 for(int i=R+1; i<C; i++) row = row*10+str[i]-'0';for(int i=C+1; i<len; i++)col = col*10+str[i]-'0';// 将十进制数转换为以 A-Z 表达的二十六进制数 int tmp;string ans;while(col > 0){tmp = col%26;if(tmp == 0){tmp = 26;col -= 26;}ans += apt[tmp];col /= 26;} reverse(ans.begin(), ans.end());// 格式化输出 cout<<ans<<row<<endl;}else{ // mode 0:ECXCEL 转 RXCY 格式 // 将二十六进制数转换为十进制数 for(int i=0; i<len; i++)if(!isdigit(str[i]))col = col*26+str[i]-'A'+1;elserow = row*10+str[i]-'0';// 格式化输出 cout<<"R"<<row<<"C"<<col<<endl;}
}int main( )
{// 输入数据cin>>T;for(int i=1; i<=T; i++){cin>>str;// 将当前的坐标表达式转换为另一种格式 transform(str);}return 0;
}
MT2188 单条件和
难度:黄金 时间限制:1秒 占用内存:128M
题目描述
“单条件” 是数理逻辑中的5种常用连接词之一,记作 “→”。它是二元运算。相当于 “如果…那么…. ”、“因为……所以……”、“只要…就.….” 等。也可称为 “蕴涵”。“p→q” 读作 “如果p,那么q”,其中 p 称为前件,q 称为后件。
其真值表如下:
如 “异或和” 为 a 1 ⨁ a 2 ⨁ … ⨁ a n a_1⨁a_2⨁…⨁a_n a1⨁a2⨁…⨁an ,我们现在要求 “单条件和”,即 a 1 → a 2 → ⋯ → a n a_1→a_2→⋯→a_n a1→a2→⋯→an,对 a 1 , a 2 , … , a n a_1,a_2,…,a_n a1,a2,…,an 做位意义上的单条件运算求和。
请按 unsigned int 类型进行运算。格式
输入格式:第一行一个整数 n n n,表示有 n n n 个需要求单条件和的整数;
第二行输入 n n n 个需要求单条件和的整数。
输出格式:输出一个 unsigned int 型的整数。样例 1
输入:10
1 2 3 4 5 6 7 8 9 10输出:4294967290
备注
对于100%的数据: 1 ≤ n ≤ 5 e 6 1≤n≤5e6 1≤n≤5e6。
相关知识点:
位运算
题解
观察题目给出的真值表不难发现:“p→q” 其实等价于执行位运算 “~p|q”(非 p 或 q)。在理解这一点后,我们便能直接写出以下代码:
/*MT2188 单条件和 用 scanf 接受输入才能得满分
*/
#include<bits/stdc++.h>
using namespace std;int main( )
{// 输入数据int n;unsigned ans, tmp;cin>>n>>ans;// 执行运算for(int i=1; i<n; i++) {scanf("%u",&tmp);ans = ~ans | tmp;}// 输出 cout<<ans<<endl; return 0;
}
MT2189 三进制计算机1
难度:黄金 时间限制:1秒 占用内存:128M
题目描述
三进制计算机,是以三进法数字系统为基础而发展的计算机。在光子计算机研究领域也有涉及。
三进制代码的一个特点是对称,即相反数的一致性,因此它和二进制代码不同,不存在无符号数的概念。这样,三进制计算机的架构也要简单、稳定、经济得多。其指令系统也更便于阅读,而且非常高效。
在一般情况下,命题不一定为真或假,还可能为未知。在三进制逻辑学中,符号 1 代表真;符号 -1 代表假;符号 0 代表未知。这种逻辑表达方式更符合计算机在人工智能方面的发展趋势,它为计算机的模糊运算和自主学习提供了可能。
在本题中,请你将输入的对称三进制数转换为对应的十进制数。对称三进制数不是用 0/1/2 表示,比较特殊,是用 1/0/-1 表示,故名对称。本题中 -1 用符号 - 表示,而 1 和 0 直接表示即可。格式
输入格式:第一输入一个整数 n n n ,表示数据组数;
接下来 n n n 行,每行输入一个对称三进制整数。
输出格式:对于第 2~n+1 行输入的每一个对称三进制整数,分别输出其十进制形式。样例 1
输入:8
-0
-1
-
0
1
1-
10
1–输出:-3
-2
-1
0
1
2
3
5备注
样例中 2 = 3 − 1 , 3 = 3 + 0 × 1 , 5 = 9 − 3 − 1 2=3-1,3=3+0 \times 1,5=9-3-1 2=3−1,3=3+0×1,5=9−3−1。
对于100%的数据: 1 ≤ n ≤ 1 e 6 1≤n≤1e6 1≤n≤1e6,输入的对称三进制数对应的整数在 int 类型范围内
。
相关知识点:
平衡三进制
题解
这道题实际上考察的是进制转换,即平衡三进制转换为十进制数。
首先我们要知道,任意 k k k 进制数(设为 A k = a 1 a 2 ⋯ a n A_k=a_1 a_2⋯a_n Ak=a1a2⋯an)转换为十进制都遵循下式:
n = ∑ i = 1 n a i k n − i n=\sum_{i=1}^na_i k^{n-i} n=i=1∑naikn−i
其中, a i a_i ai 表示该 k k k 进制数在第 i i i 位上的取数, n n n 表示其长度。
例如,二进制数 1010 转换为十进制数为:
n = a 1 k 4 − 1 + a 2 k 4 − 2 + a 3 k 4 − 3 + a 4 k 4 − 4 = 1 × 2 3 + 0 × 2 2 + 1 × 2 1 + 0 × 2 0 = 10 n=a_1 k^{4-1}+a_2 k^{4-2}+a_3 k^{4-3}+a_4 k^{4-4}=1×2^3+0×2^2+1×2^1+0×2^0=10 n=a1k4−1+a2k4−2+a3k4−3+a4k4−4=1×23+0×22+1×21+0×20=10
十六进制数 AE86 转换为十进制数为:
n = a 1 k 4 − 1 + a 2 k 4 − 2 + a 3 k 4 − 3 + a 4 k 4 − 4 = 10 × 1 6 3 + 14 × 1 6 2 + 8 × 1 6 1 + 6 × 1 6 0 = 44678 n=a_1 k^{4-1}+a_2 k^{4-2}+a_3 k^{4-3}+a_4 k^{4-4}=10×16^3+14×16^2+8×16^1+6×16^0=44678 n=a1k4−1+a2k4−2+a3k4−3+a4k4−4=10×163+14×162+8×161+6×160=44678
同样地,三进制数也满足该式。但是本题比较特殊,因为平衡三进制数中的 2 会用 -1 来表示,但这并不影响通式给出的计算方法。例如,对于题目给出的平衡三进制数:1--,其转换过程如下:
n = a 1 k 3 − 1 + a 2 k 3 − 2 + a 3 k 3 − 3 = 1 × 3 2 + ( − 1 ) × 3 1 + ( − 1 ) × 3 0 = 9 − 3 − 1 = 5 n=a_1 k^{3-1}+a_2 k^{3-2}+a_3 k^{3-3}=1×3^2+(-1)×3^1+(-1)×3^0=9-3-1=5 n=a1k3−1+a2k3−2+a3k3−3=1×32+(−1)×31+(−1)×30=9−3−1=5
根据这样的思路,可写出求解本题的完整代码:
下面给出基于以上思路写出的完整代码(已 AC):
/*MT2189 三进制计算机1 输出转换结果时不能用 endl ,否则会超时
*/
#include<bits/stdc++.h>
using namespace std;const int N = 105;
int w[N], n, ans, len;
char s[N];int main( )
{// 取消cin与stdin的同步(加速文件读取速度) ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);// 输入数据cin>>n; // 构建乘位 w[0] = 1;for(int i=1; i<=100; i++)w[i] = w[i-1]*3;// 进制转换与输出 while(n--){cin>>s;ans = 0;len = strlen(s);// 进制转换 for(int i=len-1; i>=0; i--){if(s[i] == '1') ans += w[len-1-i];if(s[i] == '-') ans -= w[len-1-i];}// 输出转换结果cout<<ans<<"\n";}return 0;
}
此外,对本题而言还需要特别注意两点:
- 必须取消 cin 与 stdin 的同步以加速文件读取速度,否则会超时(原理请见:C++中输入和输出的一些问题);
- 输出换行时必须用 “\n” 替代 “endl”,否则会超时。
当然,你也可以用 C 的方式进行数据输入输出(即用scanf和printf替代cin和cout),这样就不必担心上面的这些问题。
MT2190 三进制计算机2
难度:钻石 时间限制:1秒 占用内存:128M
题目描述
三进制计算机,是以三进法数字系统为基础而发展的计算机。在光子计算机研究领域也有涉及。
三进制代码的一个特点是对称,即相反数的一致性,因此它和二进制代码不同,不存在无符号数的概念。这样,三进制计算机的架构也要简单、稳定、经济得多。其指令系统也更便于阅读,而且非常高效。
在一般情况下,命题不一定为真或假,还可能为未知。在三进制逻辑学中,符号 1 代表真;符号 -1 代表假;符号 0 代表未知。这种逻辑表达方式更符合计算机在人工智能方面的发展趋势,它为计算机的模糊运算和自主学习提供了可能。
在本题中,请你将输入的对称三进制数转换为对应的十进制数。对称三进制数不是用 0/1/2 表示,比较特殊,是用 1/0/-1 表示,故名对称。本题中 -1 用符号 - 表示,而 1 和 0 直接表示即可。格式
输入格式:第一输入一个整数 n n n ,表示数据组数;
接下来 n n n 行,每行输入一个十进制整数。
输出格式:对于第 2~n+1 行输入的每一个十进制整数,分别输出其对称三进制形式。样例 1
输入:8
-3
-2
-1
0
1
2
3
5输出:-3
-0
-1
-
0
1
1-
10
1–备注
样例中 2 = 3 − 1 , 3 = 3 + 0 × 1 , 5 = 9 − 3 − 1 2=3-1,3=3+0 \times 1,5=9-3-1 2=3−1,3=3+0×1,5=9−3−1。
对于100%的数据: 1 ≤ n ≤ 1 e 6 1≤n≤1e6 1≤n≤1e6,输入的对称三进制数对应的整数在 int 类型范围内
。
相关知识点:
平衡三进制
题解
这道题与前一题的要求刚好相反,即要求将输入的每个十进制数转换为对称三进制数并输出。
首先我们要知道,任意十进制数 n n n 转换为 k k k 进制都遵循一个过程:
- 当前位取数为:n%k;
- 为继续向后取数(即得到更高位的数),更新数 n = n k n=\frac{n}{k} n=kn。
- 若 n = 0 ,则转换结束。
例如,将十进制数 10 转换为二进制数的过程如下:
- 第1位: n % 2 = 10 % 2 = 0 n\%2 = 10\%2 = 0 n%2=10%2=0,更新 n = n 2 = 10 2 = 5 n=\frac{n}{2}=\frac{10}{2}=5 n=2n=210=5;
- 第2位: n % 2 = 5 % 2 = 1 n\%2 = 5\%2 = 1 n%2=5%2=1,更新 n = n 2 = 5 2 = 2 n=\frac{n}{2}=\frac{5}{2}=2 n=2n=25=2;
- 第3位: n % 2 = 2 % 2 = 0 n\%2 = 2\%2 = 0 n%2=2%2=0,更新 n = n 2 = 2 2 = 1 n=\frac{n}{2}=\frac{2}{2}=1 n=2n=22=1;
- 第4位: n % 2 = 1 % 2 = 1 n\%2 = 1\%2 = 1 n%2=1%2=1,更新 n = n 2 = 1 2 = 0 n=\frac{n}{2}=\frac{1}{2}=0 n=2n=21=0,转换结束。
于是得到十进制数 10 对应的二进制数为 1010。
同样地,将十进制数转换为三进制数也遵循该算法,例如,将十进制数 11 转换为三进制数的过程如下:
- 第1位: n % 3 = 11 % 3 = 2 n\%3 = 11\%3 = 2 n%3=11%3=2,更新 n = n 3 = 11 3 = 3 n=\frac{n}{3}=\frac{11}{3}=3 n=3n=311=3;
- 第2位: n % 3 = 3 % 3 = 0 n\%3 = 3\%3 = 0 n%3=3%3=0,更新 n = n 3 = 3 3 = 1 n=\frac{n}{3}=\frac{3}{3}=1 n=3n=33=1;
- 第3位: n % 3 = 1 % 3 = 1 n\%3 = 1\%3 = 1 n%3=1%3=1,更新 n = n 3 = 1 3 = 0 n=\frac{n}{3}=\frac{1}{3}=0 n=3n=31=0,转换结束。
于是得到十进制数 11 对应的三进制数为 102。
而本题要求转换的 “平衡三进制” 中,所有的 “2” 都要求用 “-1” 来替代。这一替换实际上相当于将指定位上的值减少了 1(从这个数的整体来看,实际上减少了 1 × k p 1×k^p 1×kp),为了保证这个数在整体上的值不变,就必须向前一位借位,即将这个位前的那个值加 1。例如,由十进制数 11 得到的三进制数为 102,我们从该数的低位向高位扫描:首先,末尾存在一个 “2”,于是将这个数替换为 “-”,并将较高位的 “0” 替换为 “1”(即得到 11-);接继续向后扫描,发现整个序列中的数均合法,于是得到由十进制数 11 转换的平衡三进制数为 11-。我们可以进行验证:
n = a 1 k 3 − 1 + a 2 k 3 − 2 + a 3 k 3 − 3 = 1 × 3 2 + 1 × 3 1 + ( − 1 ) × 3 0 = 9 + 3 − 1 = 11 n=a_1 k^{3-1}+a_2 k^{3-2}+a_3 k^{3-3}=1×3^2+1×3^1+(-1)×3^0=9+3-1=11 n=a1k3−1+a2k3−2+a3k3−3=1×32+1×31+(−1)×30=9+3−1=11
考虑一种情况,三进制数 122。当将末位的 “2” 借位后,中间位的 “2” 将变成数字 “3”,即此时为 13-;对中间位而言,“3” 已经达到了这个进制下的最大值,因此要进位,于是此时该数将变为 20-;继续向高位扫描,发现最高位为 “2”,因此需要将其转换为 “-”,并向较高位借位,故最终得到 1-0-。我们可以进行验算:
122 : n = 1 × 3 2 + 2 × 3 1 + 2 × 3 0 = 9 + 6 + 2 = 17 122:n=1×3^2+2×3^1+2×3^0=9+6+2=17 122:n=1×32+2×31+2×30=9+6+2=17
1 − 0 − : n = 1 × 3 3 + ( − 1 ) × 3 2 + 0 × 3 1 + ( − 1 ) × 3 0 = 17 1-0-:n=1×3^3+(-1)×3^2+0×3^1+(-1)×3^0=17 1−0−:n=1×33+(−1)×32+0×31+(−1)×30=17
可以看出,他们最终转换为十进制均为 17。
最后还需要注意一点:平衡三进制的负数与正数之间的转换关系。实际上,题目也给出了他们之间关系的一些提示:“三进制代码的一个特点是对称,即相反数的一致性”。对于平衡三进制的数而言,它的相反数与其本身的关系如下:所有非 0 数据互相相反。例如,平衡三进制数 1-01,它对应的负数则为 -10-:
1 − 01 : n = 1 × 3 3 + ( − 1 ) × 3 2 + 0 × 3 1 + 1 × 3 0 = 27 − 9 + 0 + 1 = 19 1-01:n=1×3^3+(-1)×3^2+0×3^1+1×3^0=27-9+0+1=19 1−01:n=1×33+(−1)×32+0×31+1×30=27−9+0+1=19
− 10 − : n = ( − 1 ) × 3 3 + 1 × 3 2 + 0 × 3 1 + ( − 1 ) × 3 0 = − 27 + 9 + 0 − 1 = − 19 -10-:n=(-1)×3^3+1×3^2+0×3^1+(-1)×3^0=-27+9+0-1=-19 −10−:n=(−1)×33+1×32+0×31+(−1)×30=−27+9+0−1=−19
根据上面的分析,可以将求解本题的思路整理如下:
- 将输入的十进制数转换为对应的三进制数(为便于处理,这一阶段将统一使用该数的正数);
- 将三进制数转换为平衡三进制数,转换规则如下(假设当前的三进制数字符串为num):
- 若 num[i] = 2,则令 num[i] = -, num[i+1]++(数字串的索引大小与数的低位到高位对应);
- 若 num[i] = 3,则令 num[i] = 0, num[i+1]++。
- 根据输入十进制数的正负性,对得到的平衡三进制数进行相应处理。
下面给出基于以上思路得到的完整代码(已 AC):
/*MT2190 三进制计算机2 思路:先将数从十进制转换至正常的三进制,然后再转换为平衡三进制
*/
#include<bits/stdc++.h>
using namespace std;const int N = 55;
int num[N], n, x, flag, cnt;int main( )
{// 取消cin与stdin的同步(加速文件读取速度) ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);// 输入数据cin>>n; while(n--){cin>>x;memset(num, 0, sizeof(num));flag = 1, cnt = 0;// 程序将统一处理正数,因此定义标记来记录原始输入数据的正负性 if(x<0){flag = -1;x = -x;}if(x == 0){cout<<x<<"\n";continue;} // 将十进制数转换为三进制数 while(x){num[cnt++] = x%3;x /= 3;}// 将三进制数转换为平衡三进制数 for(int i=0; i<cnt; i++){if(num[i] == 2){// 借位 num[i] = -1;num[i+1]++;}else if(num[i] == 3){// 进位 num[i] = 0;num[i+1]++; }}// 判断原始三进制数转换为平衡三进制数后是否出现了位增情况 if(num[cnt]) cnt++;// 如果原始输入的十进制数为负数,则需要对已经算出的平衡三进制数进行反号 if(flag == -1) for(int i=cnt-1; i>=0; i--)num[i] = -num[i];// 输出转换后的平衡三进制数,需要进行格式控制:所有的-1都输出- for(int i=cnt-1; i>=0; i--)if(num[i] == -1) cout<<"-";else cout<<num[i];cout<<"\n";}return 0;
}
END
相关文章:

【马蹄集】第二十三周——进位制专题
进位制专题 目录 MT2186 二进制?不同!MT2187 excel的烦恼MT2188 单条件和MT2189 三进制计算机1MT2190 三进制计算机2 MT2186 二进制?不同! 难度:黄金 时间限制:1秒 占用内存:128M 题目…...

[足式机器人]Part3 变分法Ch01-1 数学预备知识——【读书笔记】
本文仅供学习使用 本文参考: 《变分法基础-第三版》老大中 《变分学讲义》张恭庆 《Calculus of Variations of Optimal Control Theory》-变分法和最优控制论-Daneil Liberzon Ch01-1 数学基础-预备知识1 1 数学基础-预备知识1.1 泰勒公式1.1.1 一元函数的泰勒公式…...

计算机网络----CRC冗余码的运算
目录 1. 冗余码的介绍及原理2. CRC检验编码的例子3. 小练习 1. 冗余码的介绍及原理 冗余码是用于在数据链路层的通信链路和传输数据过程中可能会出错的一种检错编码方法(检错码)。原理:发送发把数据划分为组,设每组K个比特&#…...
将Nginx源码数组结构(ngx_array.c)和内存池代码单独编译运行,附代码
在上面一篇的基础上把Nginx源码数组结构也摘录下来,也增加了测试代码,编译运行。 https://blog.csdn.net/katerdaisy/article/details/132358883 《将nginx内存池代码单独编译运行,了解nginx内存池工作原理,附代码》 核心代码&…...
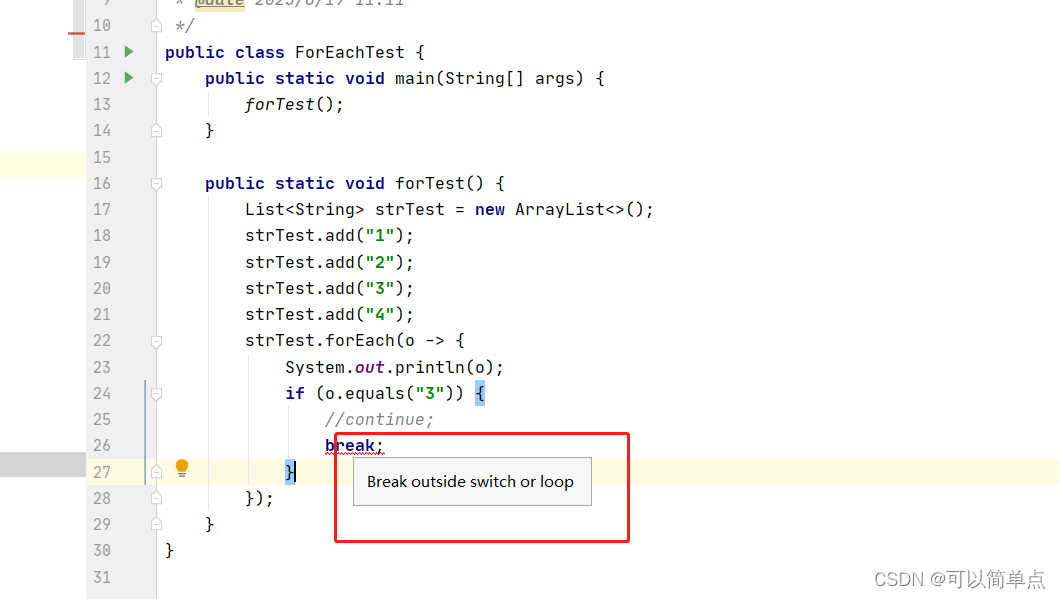
java forEach中不能使用break和continue的原因
1.首先了解break和continue的使用范围和作用 1.1使用范围 break适用范围:只能用于switch或者是循环语句中。当然可以用于增强for循环。 continue适用范围: 用于循环语句中。 1.2作用 break: 1. break用于switch语句的作用是结束一个switch语句。 2. break用于循…...

[杂项]水浒英雄谱系列电影列表
年份 片名 导演 主演 2006-01-01 母夜叉孙二娘 张建亚 周海媚 、 莫少聪 、 于承惠 [1] 2008-01-01 碧瑶霜迷案 黄祖权 陈龙 、 陈德容 、 翁家明 [7] 2008-05-09 青面兽杨志 张建亚 吕良伟 、 计春华 、 孟广美 [2] 2008-05-09 扈三娘与矮脚虎王英 张建亚 曾宝仪 、 郭德纲 、…...

6.RocketMQ之索引文件ConsumeQueue
本文着重分析为consumequeue/topic/queueId目录下的索引文件。 1.ConsumeQueueStore public class ConsumeQueueStore {protected final ConcurrentMap<String>, ConcurrentMap<Integer>, ConsumeQueueInterface>> consumeQueueTable;public boolean load(…...

【C++学习手札】一文带你认识C++虚继承
食用指南:本文在有C基础的情况下食用更佳 🍀本文前置知识:C虚函数(很重要,内部剖析) ♈️今日夜电波:僕らのつづき—柊優花 1:06 ━━━━━━️💟──────── 3:51 …...

神经网络基础-神经网络补充概念-63-残差网络
概念 残差网络(Residual Network,ResNet)是一种深度卷积神经网络结构,旨在解决深层网络训练中的梯度消失和梯度爆炸问题,以及帮助训练非常深的网络。ResNet 在2015年被提出,其核心思想是引入了"残差块…...
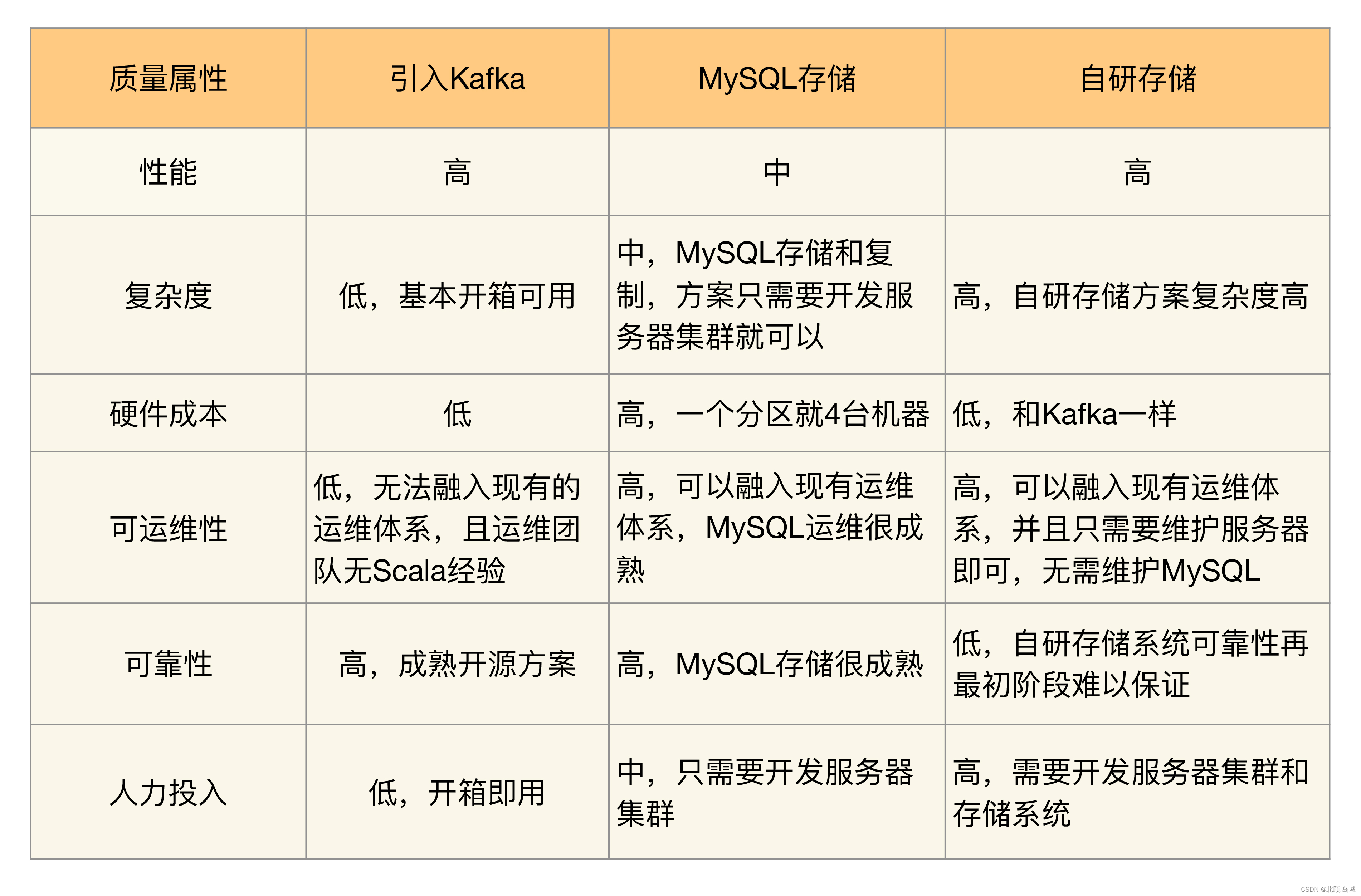
【从0开始学架构笔记】01 基础架构
文章目录 一、架构的定义1. 系统与子系统2. 模块与组件3. 框架与架构4. 重新定义架构 二、架构设计的目的三、复杂度来源:高性能1. 单机复杂度2. 集群复杂度2.1 任务分配2.2 任务分解(微服务) 四、复杂度来源:高可用1. 计算高可用…...

vue3+ts+vite使用el-breadcrumb实现面包屑组件,实现面包屑过渡动画
简介 使用 element-plus 的 el-breadcrumb 组件,实现根据页面路由动态生成面包屑导航,并实现面包屑导航的切换过渡动画 一、先看效果加粗样式 1.1 静态效果 1.2 动态效果 二、全量代码 <script lang"ts" setup> import { ref, watch…...
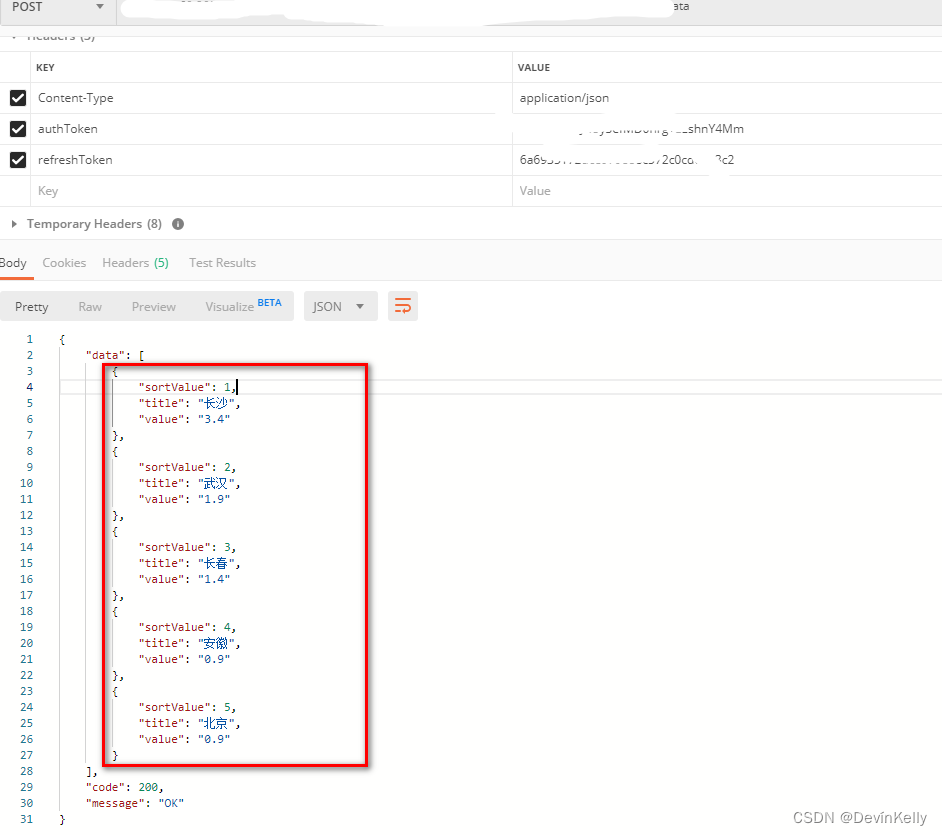
【Java 动态数据统计图】动态数据统计思路案例(动态,排序,数组)四(116)
需求::前端根据后端的返回数据:画统计图; 1.动态获取地域数据以及数据中的平均值,按照平均值降序排序; 说明: X轴是动态的,有对应区域数据则展示; X轴 区域数据降序排序…...

Chrome命令行开关
Electron 支持的命令行开关 –client-certificatepath 设置客户端的证书文件 path . –ignore-connections-limitdomains 忽略用 , 分隔的 domains 列表的连接限制. –disable-http-cache 禁止请求 HTTP 时使用磁盘缓存. –remote-debugging-portport 在指定的 端口 通…...

元宇宙赛道加速破圈 和数软件抓住“元宇宙游戏”发展新风口
当下海外游戏市场仍然具备较大的增长空间。据机构预测,至2025年全球移动游戏市场规模将达1606亿美元,对应2020-2025年复合增长率11%。与此同时,随着元宇宙概念持续升温,国内外多家互联网巨头纷纷入场。行业分析平台New…...

Vue的鼠标键盘事件
Vue的鼠标键盘事件 原生 鼠标事件(将v-on简写为) click // 点击 dblclick // 双击 mousedown // 按下 mousemove // 移动 mouseleave // 离开 mouseout // 移出 mouseenter // 进入 mouseover // 鼠标悬浮mousedown.left 键盘事件 keydown //键盘按下时触发 keypress …...

Bytebase 2.6.0 - 支持通过 LDAP 配置 SSO,支持 RisingWave 数据库
🚀 新功能 支持通过 LDAP 配置 SSO。支持增加多个只读连接。Schema 模版支持列类型约束。支持 RisingWave 数据库。库表同步功能支持 TiDB。数据脱敏功能支持 SQL Server。SQL 审核 CI 功能支持 Azure DevOps。 🎄 改进 支持设置数据库的环境与所属实…...
C# 读取pcd、ply点云文件数据
最近研究了下用pcl读取点云数据,又做了个C#的dll,方便读取,同样这个dll基于pcl 最新版本1.13.1版本开发。 上次做的需要先得到点云长度,再获取数据。这次这个定义了一个PointCloudXYZ类来存数据。将下面的dll拷贝到可执行目录下&a…...

LeetCode1387 将整数按权重排序
思路 首先是这种计算权重的方式很有可能出现重复,所以需要记忆化搜索记忆化搜索:先查表再计算,先存表再返回。将整数 x 和计算的权重分别存储数组的0和1的位置重写compare将数组排序按规则排序返回结果 代码 class Solution {private Hash…...

正则表达式--Intellij IDEA常用的替换
原文网址:正则表达式--Intellij IDEA常用的替换_IT利刃出鞘的博客-CSDN博客 简介 本文介绍IDEA使用正则表达式进行替换时的常用的一些示例。 根据注释加注解 需求 将 /*** abc*/ 改为: /*** abc*/ ApiModelOperation("abc") 方法 选…...
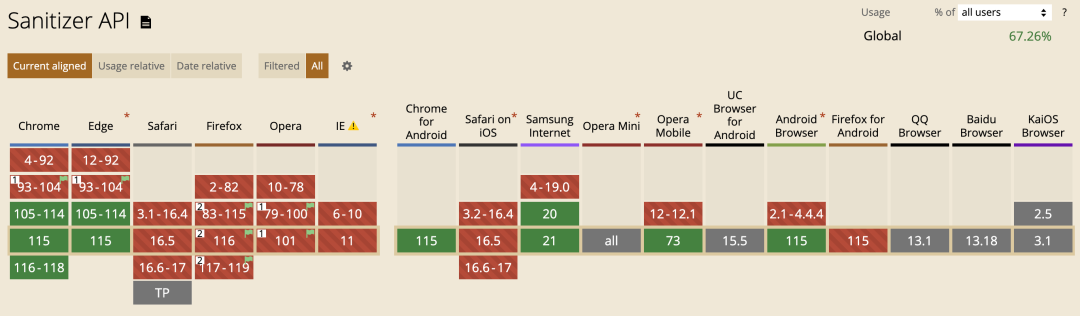
前端如何安全的渲染HTML字符串?
在现代的Web 应用中,动态生成和渲染 HTML 字符串是很常见的需求。然而,不正确地渲染HTML字符串可能会导致安全漏洞,例如跨站脚本攻击(XSS)。为了确保应用的安全性,我们需要采取一些措施来在安全的环境下渲染…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...
