AC的改进算法——TRPO、PPO
两类AC的改进算法
整理了动手学强化学习的学习内容
1. TRPO 算法(Trust Region Policy Optimization)
1.1. 前沿
策略梯度算法即沿着梯度方向迭代更新策略参数 。但是这种算法有一个明显的缺点:当策略网络沿着策略梯度更新参数,可能由于步长太长,策略突然显著变差,进而影响训练效果。
针对以上问题,考虑在更新时找到一块信任区域(trust region),在这个区域上更新策略时能够得到某种策略性能的安全性保证,这就是信任区域策略优化(trust region policy optimization,TRPO)算法的主要思想。
1.2. 一些推导
首先,最常规的动作价值函数,状态价值函数,优势函数定义如下:
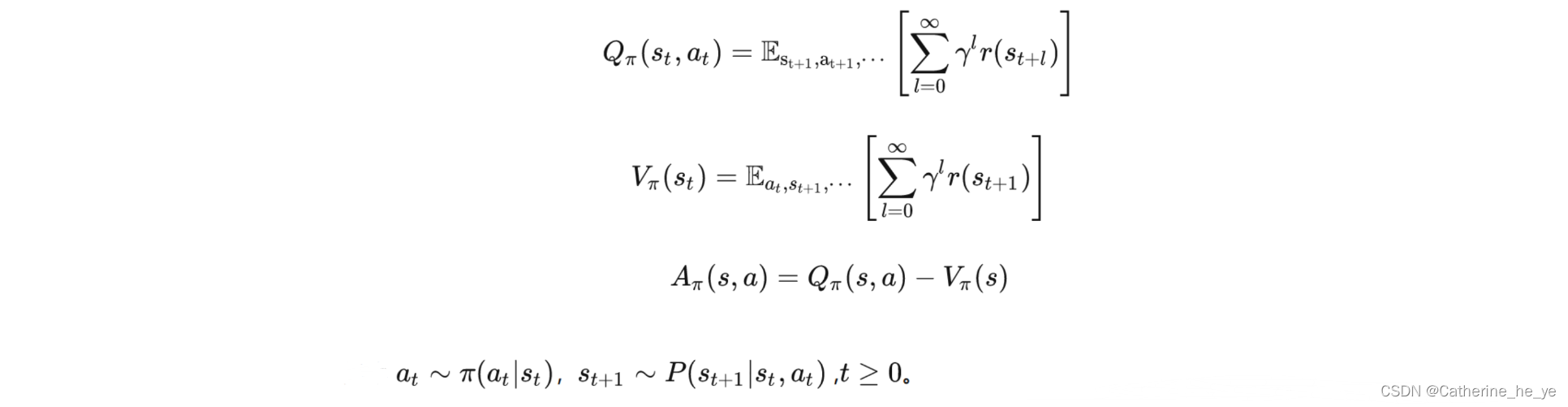 接着,一个策略的好坏可以期望折扣奖励J(πθ)J(\pi_\theta)J(πθ)表示:
接着,一个策略的好坏可以期望折扣奖励J(πθ)J(\pi_\theta)J(πθ)表示:
J(πθ)=Es0,a0,...[∑t=0∞γtr(st)]=Es0[Vπθ(s0)]J(\pi_\theta)=E_{s_0,a_0,...}[\sum_{t=0}^{\infty}\gamma^tr(s_t)]=E_{s_0}[V^{\pi_\theta}(s_0)]J(πθ)=Es0,a0,...[t=0∑∞γtr(st)]=Es0[Vπθ(s0)]
其中,s0∼ρ0(s0)s_0 \sim \rho_0(s_0)s0∼ρ0(s0),at∼πθ(at∣st)a_t \sim \pi_\theta(a_t|s_t)at∼πθ(at∣st),at+1∼P(st+1∣st,at)a_{t+1} \sim P(s_{t+1}|s_t,a_t)at+1∼P(st+1∣st,at)。
由于初始状态s0s_0s0的分布ρ0\rho_0ρ0和策略无关,因此上述策略πθ\pi_\thetaπθ下的优化目标J(πθ)J(\pi_\theta)J(πθ)可以写成在新策略πθ′\pi_{\theta'}πθ′的期望形式:
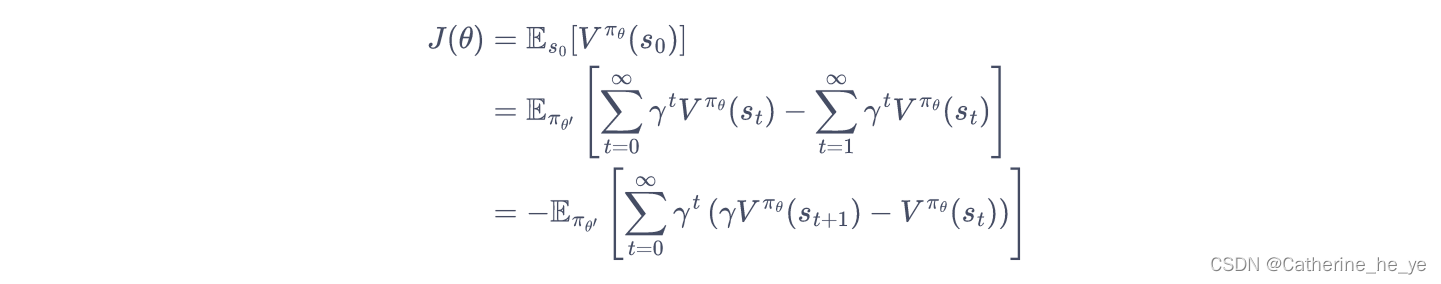 从而,推导新旧策略的目标函数之间的差距:
从而,推导新旧策略的目标函数之间的差距:
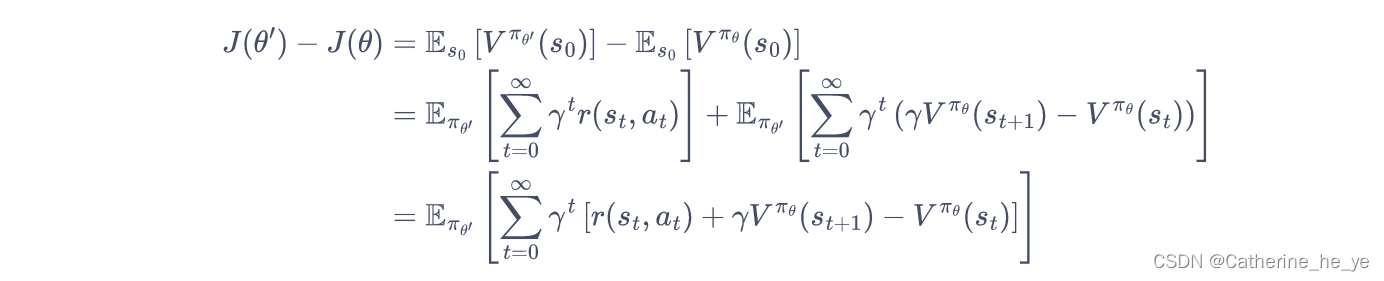 将时序差分残差定义为优势函数A:
将时序差分残差定义为优势函数A:
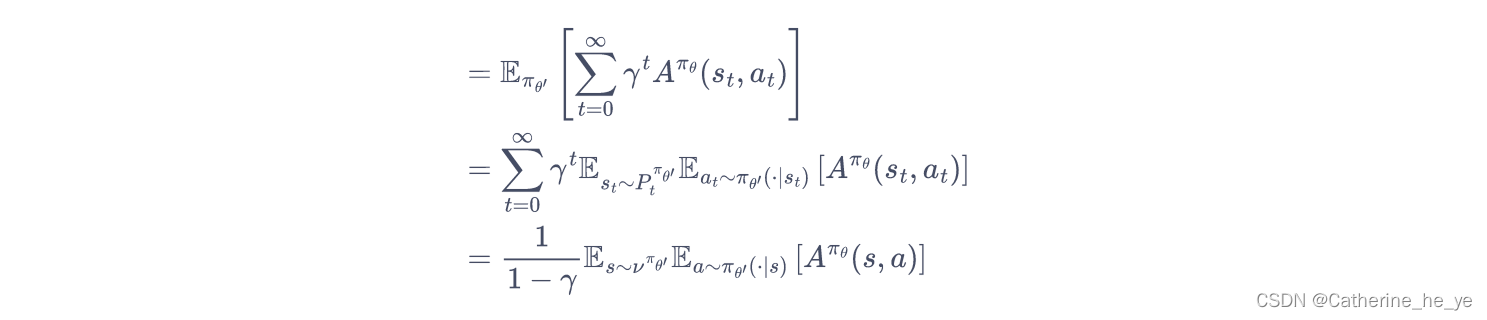 所以只要我们能找到一个新策略,使得J(θ′)−J(θ)>=0J(\theta')-J(\theta)>=0J(θ′)−J(θ)>=0,就能保证策略性能单调递增。
所以只要我们能找到一个新策略,使得J(θ′)−J(θ)>=0J(\theta')-J(\theta)>=0J(θ′)−J(θ)>=0,就能保证策略性能单调递增。
但是直接求解该式是非常困难的,因为πθ′\pi_{\theta'}πθ′是我们需要求解的策略,但我们又要用它来收集样本。把所有可能的新策略都拿来收集数据,然后判断哪个策略满足上述条件的做法显然是不现实的。
于是 TRPO 做了一步近似操作,对状态访问分布进行了相应处理。具体而言,忽略两个策略之间的状态访问分布变化,直接采用旧的策略的状态分布,定义如下替代优化目标:
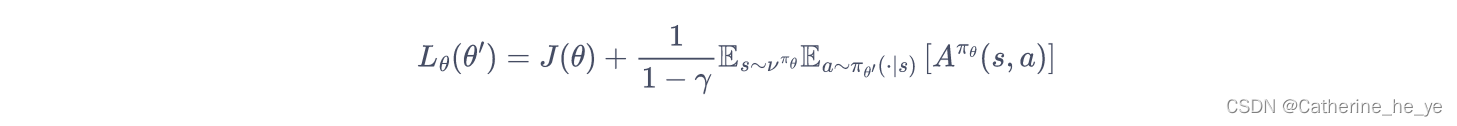 当新旧策略非常接近时,状态访问分布变化很小,这么近似是合理的。其中,动作仍然用新策略πθ′\pi_{\theta'}πθ′采样得到,我们可以用重要性采样对动作分布进行处理:
当新旧策略非常接近时,状态访问分布变化很小,这么近似是合理的。其中,动作仍然用新策略πθ′\pi_{\theta'}πθ′采样得到,我们可以用重要性采样对动作分布进行处理:
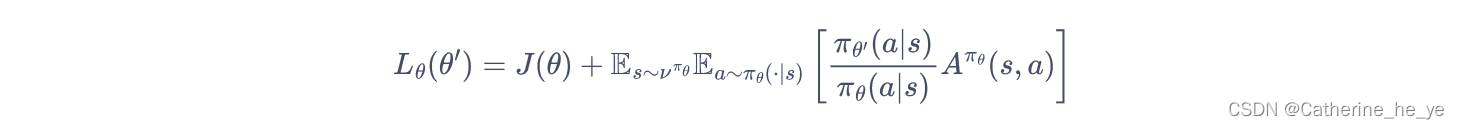 为了保证新旧策略足够接近,TRPO 使用了KL散度来衡量策略之间的距离,并给出了整体的优化公式:
为了保证新旧策略足够接近,TRPO 使用了KL散度来衡量策略之间的距离,并给出了整体的优化公式:
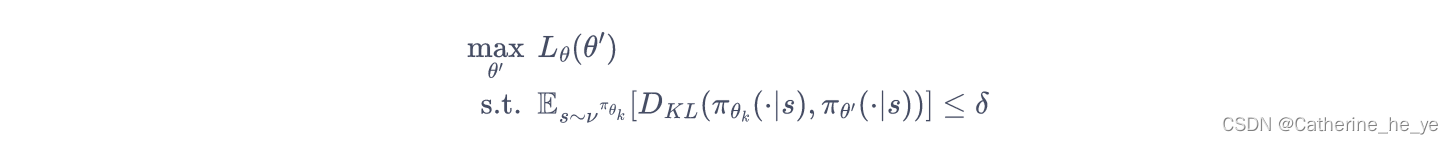 这里的不等式约束定义了策略空间中的一个 KL 球,被称为信任区域。在这个区域中,可以认为当前学习策略和环境交互的状态分布与上一轮策略最后采样的状态分布一致,进而可以基于一步行动的重要性采样方法使当前学习策略稳定提升。
这里的不等式约束定义了策略空间中的一个 KL 球,被称为信任区域。在这个区域中,可以认为当前学习策略和环境交互的状态分布与上一轮策略最后采样的状态分布一致,进而可以基于一步行动的重要性采样方法使当前学习策略稳定提升。
1.3. 近似求解
直接求解上式带约束的优化问题比较麻烦,TRPO 在其具体实现中做了一步近似操作来快速求解。
对目标函数和约束在θk\theta_kθk进行泰勒展开,分别用 1 阶、2 阶进行近似:
 于是我们的优化目标变成了:
于是我们的优化目标变成了:
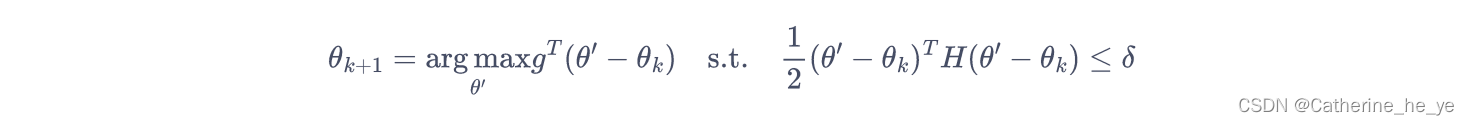 此时,我们可以用KKT条件直接导出上述问题的解:
此时,我们可以用KKT条件直接导出上述问题的解:
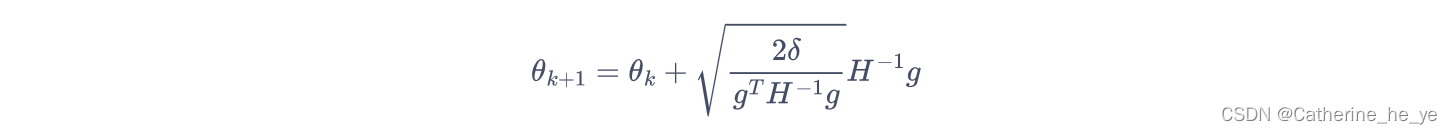
1.4. 共轭梯度
一般来说,用神经网络表示的策略函数的参数数量都是成千上万的,计算和存储黑塞矩阵的逆矩阵会耗费大量的内存资源和时间。
TRPO 通过共轭梯度法(conjugate gradient method)回避了这个问题,它的核心思想是直接计算x=H−1gx=H^{-1}gx=H−1g,xxx即参数更新方向。假设满足 KL距离约束的参数更新时的最大步长为β=θ′−θ\beta=\theta'-\thetaβ=θ′−θ。
于是,根据 KL 距离约束条件12(θ′−θk)TH(θ′−θk)<=δ\frac{1}{2}(\theta'-\theta_k)^TH(\theta'-\theta_k)<=\delta21(θ′−θk)TH(θ′−θk)<=δ,有12(βx)TH(βx)=δ\frac{1}{2}(\beta x)^TH(\beta x)=\delta21(βx)TH(βx)=δ。求解β\betaβ,得到β=2δxTHx\beta=\sqrt{\frac{2\delta}{x^THx}}β=xTHx2δ。因此,此时参数更新方式为
θk+1=θk+2δxTHxx\theta_{k+1}=\theta_k+\sqrt{\frac{2\delta}{x^THx}}xθk+1=θk+xTHx2δx,
因此,只要可以直接计算x=H−1gx=H^{-1}gx=H−1g,就可以根据该式更新参数,问题转化为解Hx=gHx=gHx=g。实际上HHH为对称正定矩阵,所以我们可以使用共轭梯度法来求解。
共轭梯度法的具体流程如下:
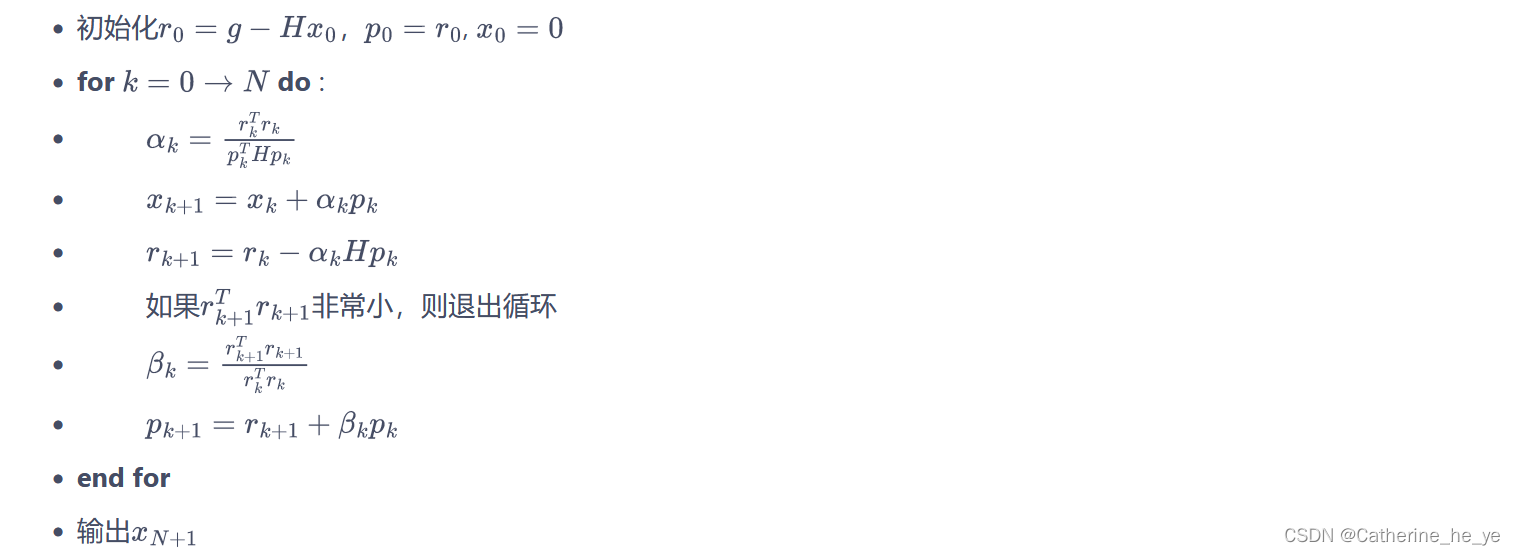 在共轭梯度运算过程中,直接计算αk\alpha_kαk和rk+1r_{k+1}rk+1需要计算和存储海森矩阵HHH。为了避免这种大矩阵的出现,我们只计算HxHxHx向量,而不直接计算和存储HHH矩阵。这样做比较容易,因为对于任意的列向量vvv,容易验证:
在共轭梯度运算过程中,直接计算αk\alpha_kαk和rk+1r_{k+1}rk+1需要计算和存储海森矩阵HHH。为了避免这种大矩阵的出现,我们只计算HxHxHx向量,而不直接计算和存储HHH矩阵。这样做比较容易,因为对于任意的列向量vvv,容易验证:
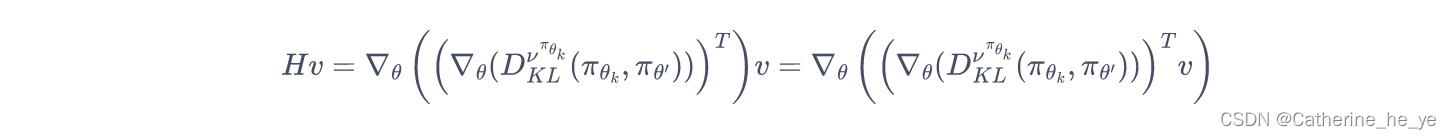 即先用梯度和向量vvv点乘后计算梯度。
即先用梯度和向量vvv点乘后计算梯度。
def hessian_matrix_vector_product(self, states, old_action_dists, vector):# 计算黑塞矩阵和一个向量的乘积new_action_dists = torch.distributions.Categorical(self.actor(states))kl = torch.mean(torch.distributions.kl.kl_divergence(old_action_dists,new_action_dists)) # 计算平均KL距离kl_grad = torch.autograd.grad(kl,self.actor.parameters(),create_graph=True)kl_grad_vector = torch.cat([grad.view(-1) for grad in kl_grad])# KL距离的梯度先和向量进行点积运算kl_grad_vector_product = torch.dot(kl_grad_vector, vector)grad2 = torch.autograd.grad(kl_grad_vector_product,self.actor.parameters())grad2_vector = torch.cat([grad.view(-1) for grad in grad2])return grad2_vectordef conjugate_gradient(self, grad, states, old_action_dists): # 共轭梯度法求解方程x = torch.zeros_like(grad)r = grad.clone()p = grad.clone()rdotr = torch.dot(r, r)for i in range(10): # 共轭梯度主循环Hp = self.hessian_matrix_vector_product(states, old_action_dists,p)alpha = rdotr / torch.dot(p, Hp)x += alpha * pr -= alpha * Hpnew_rdotr = torch.dot(r, r)if new_rdotr < 1e-10:breakbeta = new_rdotr / rdotrp = r + beta * prdotr = new_rdotrreturn x
1.5. 线性搜索
由于 TRPO 算法用到了泰勒展开的 1 阶和 2 阶近似,这并非精准求解,因此,θ\thetaθ可能未必比θk\theta_kθk好,或未必能满足 KL 散度限制。TRPO 在每次迭代的最后进行一次线性搜索,以确保找到满足条件。具体来说,就是找到一个最小的非负整数iii,使得按照
θk+1=θk+αi2δxTHxx\theta_{k+1}=\theta_{k}+\alpha^i \sqrt{\frac{2\delta}{x^THx}}xθk+1=θk+αixTHx2δx
求出的θk+1\theta_{k+1}θk+1依然满足最初的 KL 散度限制,并且确实能够提升目标函数,这KaTeX parse error: Undefined control sequence: \apha at position 1: \̲a̲p̲h̲a̲ ̲\in (0,1)其中是一个决定线性搜索长度的超参数。
1.6. 总结
至此,我们已经基本上清楚了 TRPO 算法的大致过程,它具体的算法流程如下:

2. PPO 算法(Trust Region Policy Optimization)
2.1. 前沿
PPO 算法作为TRPO算法的改进版,但是其算法实现更加简单。并且大量的实验结果表明,与TRPO相比,PPO能学习得一样好(甚至更快),这使得PPO成为非常流行的强化学习算法。如果我们想要尝试在一个新的环境中使用强化学习算法,那么 PPO 就属于可以首先尝试的算法。
PPO 的优化目标与 TRPO 相同,但 PPO用了一些相对简单的方法来求解(TRPO 使用泰勒展开近似、共轭梯度、线性搜索等方法直接求解)。具体来说,PPO 有两种形式,一是 PPO-惩罚,二是 PPO-截断,接下来对这两种形式进行介绍。
2.2. PPO-惩罚
PPO-Penalty用拉格朗日乘数法直接将 KL 散度的限制放进了目标函数中,这就变成了一个无约束的优化问题,在迭代的过程中不断更新 KL 散度前的系数。即:
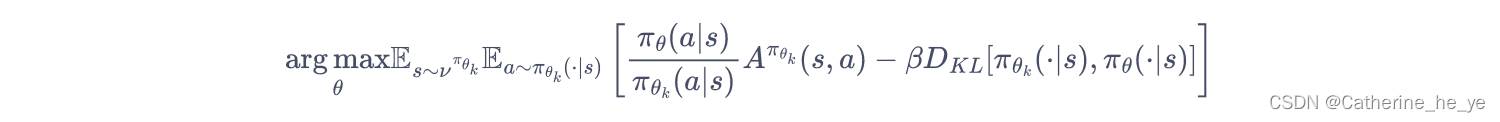 令dk=DKLπθk(πθk,πθ)d_k=D_{KL}^{\pi_{\theta_k}}(\pi_{\theta_k},\pi_{\theta})dk=DKLπθk(πθk,πθ),β\betaβ的更新规则如下:
令dk=DKLπθk(πθk,πθ)d_k=D_{KL}^{\pi_{\theta_k}}(\pi_{\theta_k},\pi_{\theta})dk=DKLπθk(πθk,πθ),β\betaβ的更新规则如下:
- 如果dk<δ/1.5d_k<\delta/1.5dk<δ/1.5,那么βk+1=βk/2\beta_{k+1}=\beta_k/2βk+1=βk/2
- 如果dk>δ×1.5d_k>\delta \times 1.5dk>δ×1.5,那么βk+1=βk×2\beta_{k+1}=\beta_k \times 2βk+1=βk×2
- 否则βk+1=βk\beta_{k+1}=\beta_kβk+1=βk
其中,δ\deltaδ是事先设定的一个超参数,用于限制学习策略和之前一轮策略的差距。
2.3 PPO-截断
PPO的另一种形式 PPO-截断(PPO-Clip) 更加直接,它在目标函数中进行限制,以保证新的参数和旧的参数的差距不会太大,即:
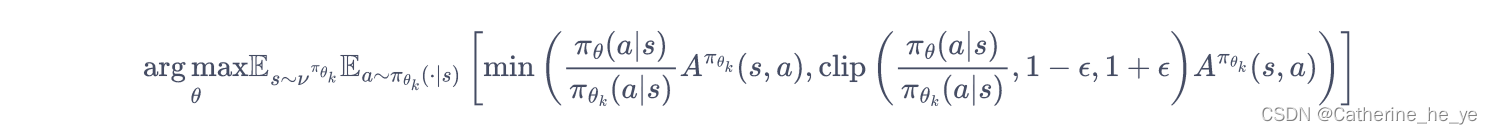 其中clip(x,l,r):=max(min(x,r),l)clip(x,l,r):=max(min(x,r),l)clip(x,l,r):=max(min(x,r),l) ,即把xxx限制在[l,r][l,r][l,r]内。上式中ϵ\epsilonϵ是一个超参数,表示进行截断(clip)的范围。
其中clip(x,l,r):=max(min(x,r),l)clip(x,l,r):=max(min(x,r),l)clip(x,l,r):=max(min(x,r),l) ,即把xxx限制在[l,r][l,r][l,r]内。上式中ϵ\epsilonϵ是一个超参数,表示进行截断(clip)的范围。
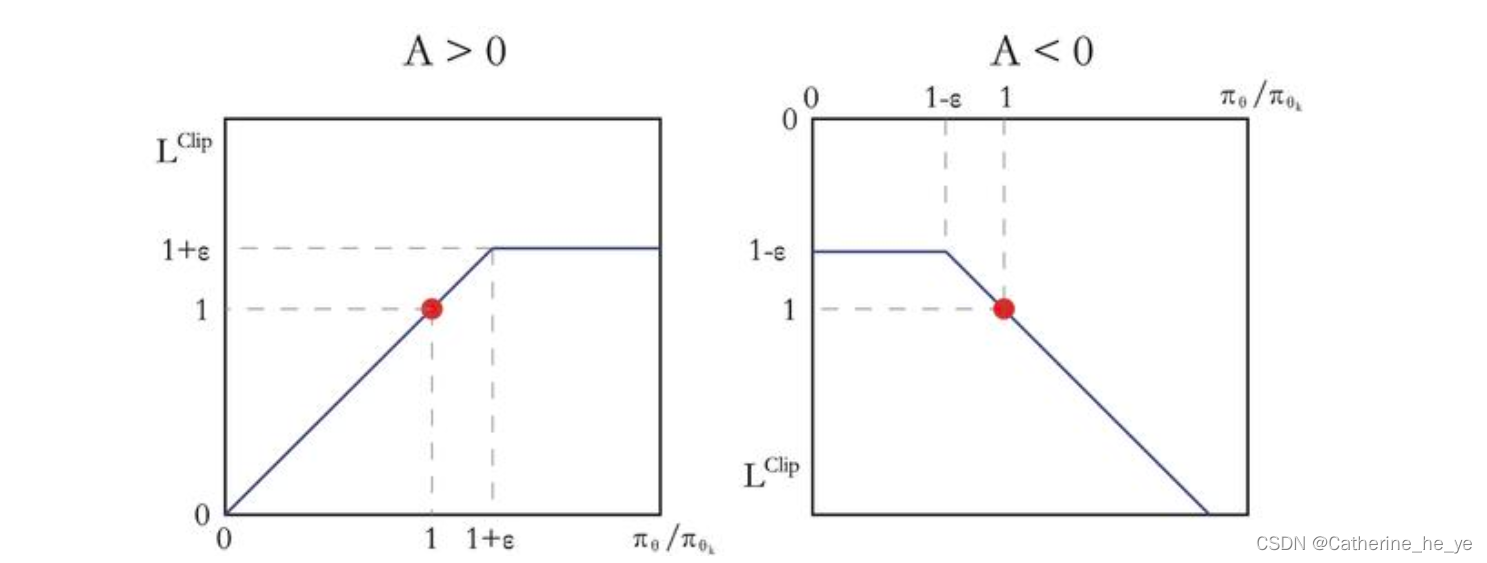
如果Aπθk(s,a)>0A^{\pi_{\theta_k}}(s,a)>0Aπθk(s,a)>0,说明这个动作的价值高于平均,最大化这个式子会增大πθ(a∣s)πθk(a∣s)\frac{\pi_\theta (a|s)}{\pi_{\theta_k} (a|s)}πθk(a∣s)πθ(a∣s),但不会让其超过1+ϵ1+\epsilon1+ϵ。反之,如果Aπθk(s,a)<0A^{\pi_{\theta_k}}(s,a)<0Aπθk(s,a)<0,最大化这个式子会减小πθ(a∣s)πθk(a∣s)\frac{\pi_\theta (a|s)}{\pi_{\theta_k} (a|s)}πθk(a∣s)πθ(a∣s),但不会让其超过1−ϵ1-\epsilon1−ϵ。如下图所示。
代码
最后,两个算法的代码可参考GitHub,Good Night!
相关文章:

AC的改进算法——TRPO、PPO
两类AC的改进算法 整理了动手学强化学习的学习内容 1. TRPO 算法(Trust Region Policy Optimization) 1.1. 前沿 策略梯度算法即沿着梯度方向迭代更新策略参数 。但是这种算法有一个明显的缺点:当策略网络沿着策略梯度更新参数,…...
【C++学习】list的使用及模拟实现
🐱作者:一只大喵咪1201 🐱专栏:《C学习》 🔥格言:你只管努力,剩下的交给时间! list的使用及模拟实现😼构造函数🐵模拟实现😼迭代器🐵…...

动态规划专题精讲1
致前行的人: 要努力,但不要着急,繁花锦簇,硕果累累都需要过程! 前言: 本篇文章为大家带来一种重要的算法题,就是动态规划类型相关的题目,动态规划类的题目在笔试和面试中是考察非常高…...
PPO(proximal policy optimization)算法
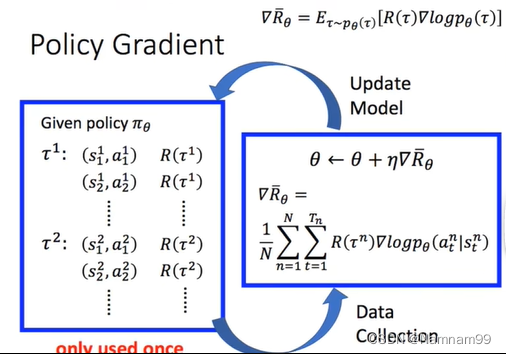
博客写到一半发现有篇讲的很清楚,直接化缘了 https://www.jianshu.com/p/9f113adc0c50 Policy gradient 强化学习的目标:学习到一个策略πθ(a∣s)\pi\theta(a|s)πθ(a∣s)来最大化期望回报。 一种直接的方法就是在策略空间中直接搜索来得到最优策略&…...

ElasticSearch基本使用
title: ElasticSearch基本使用 date: 2022-08-29 00:00:00 tags: ElasticSearch基本使用 categories:ElasticSearch 基本概念 随着ES版本的升级,文中有些概念可能已经废弃。 索引词(term) 一个能够被索引的精确值,区分大小写,可以通过term查…...
windows微软商店下载应用失败/下载故障的解决办法;如何在网页上下载微软商店的应用
一、问题背景 设置惠普打印机时,需要安装hp smart,但是官方只提供微软商店这一下载渠道。 点击安装HP Smart,确定进入微软商店下载。 完全加载不出来,可能是因为开了代理。 把代理关了,就能正常打开了。 但是点击“…...
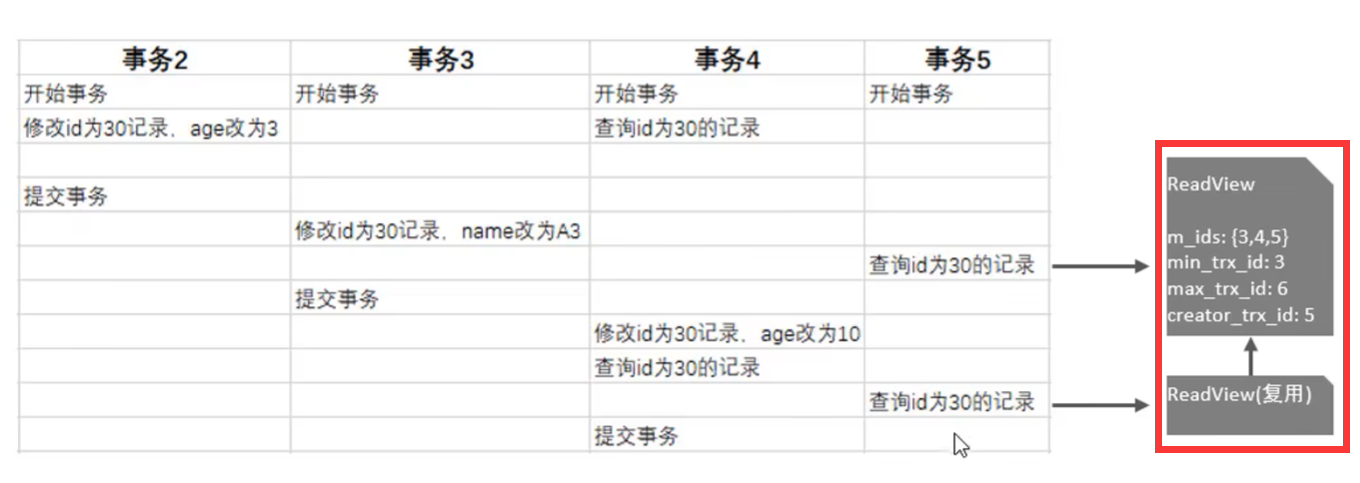
MySQL进阶篇之InnoDB存储引擎
06、InnoDB引擎 6.1、逻辑存储结构 表空间(Tablespace) 表空间在MySQL中最终会生成ibd文件,一个mysql实例可以对应多个表空间,用于存储记录、索引等数据。 段(Segment) 段,分为数据段&#x…...

商标侵权行为的种类有哪些
商标侵权行为的种类有哪些 1、商标侵权行为的种类有以下七种: (1)未经商标注册人的许可,在同一种商品上使用与其注册商标相同的商标的; (2)未经商标注册人的许可,在同一种商品上使用与其注册商标近似的商标,或者在类似商品上使…...
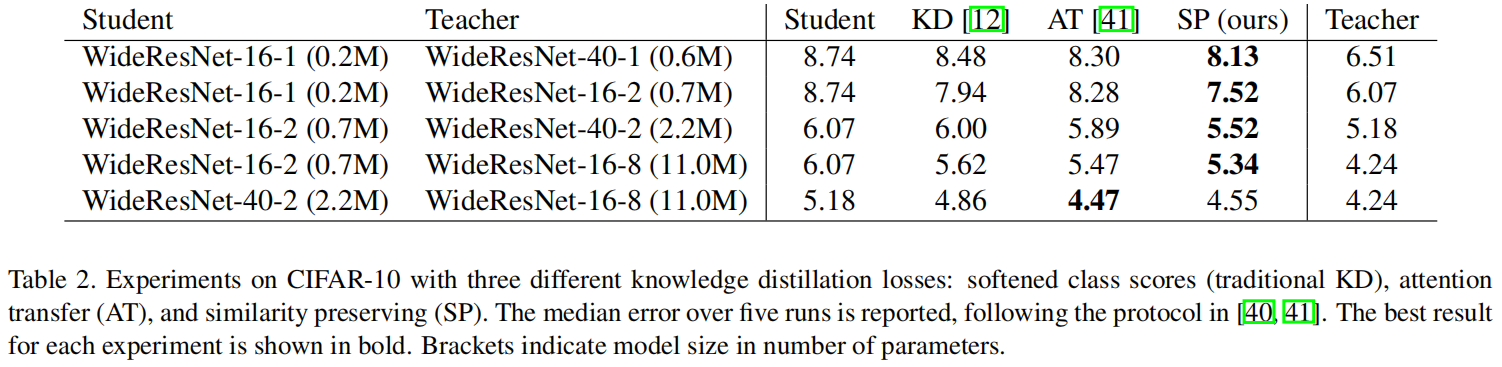
Similarity-Preserving KD(ICCV 2019)原理与代码解析
paper:Similarity-Preserving Knowledge Distillationcode:https://github.com/megvii-research/mdistiller/blob/master/mdistiller/distillers/SP.py背景本文的灵感来源于作者观察到在一个训练好的网络中,语义上相似的输入倾向于引起相似的…...
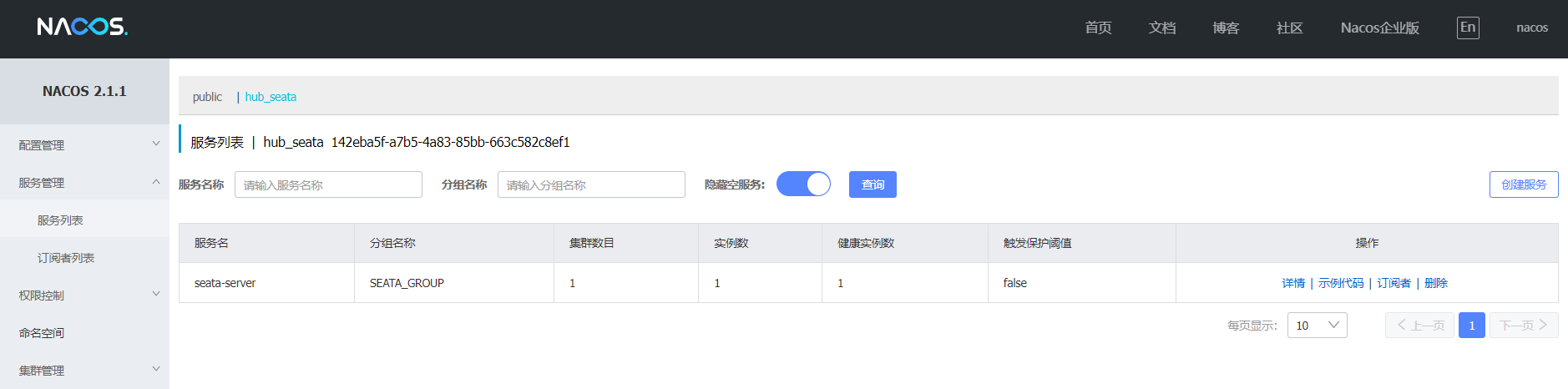
在Linux和Windows上安装seata-1.6.0
记录:381场景:在CentOS 7.9操作系统上,安装seata-1.6.0。在Windows上操作系统上,安装seata-1.6.0。Seata,一款开源的分布式事务解决方案,致力于提供高性能和简单易用的分布式事务服务。版本:JDK…...

兼职任务平台收集(二)分享给有需要的朋友们
互联网时代,给人们带来了很大的便利。信息交流、生活缴费、足不出户购物、便捷出行、线上医疗、线上教育等等很多。可以说,网络的时代会一直存在着。很多人也在互联网上赚到了第一桶金,这跟他们的努力和付出是息息相关的。所谓一份耕耘&#…...
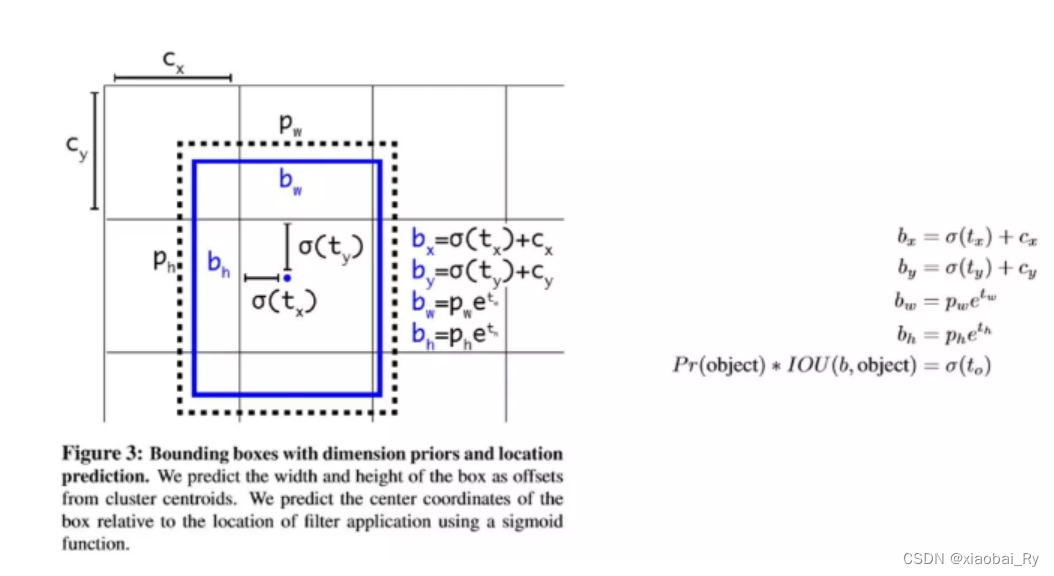
目标检测三大数据格式VOC,YOLO,COCO的详细介绍
注:本文仅供学习,未经同意请勿转载 说明:该博客来源于xiaobai_Ry:2020年3月笔记 对应的PDF下载链接在:待上传 目录 目标检测常见数据集总结 V0C数据集(Annotation的格式是xmI) A. 数据集包含种类: B. V0C2007和V0C2012的区别…...
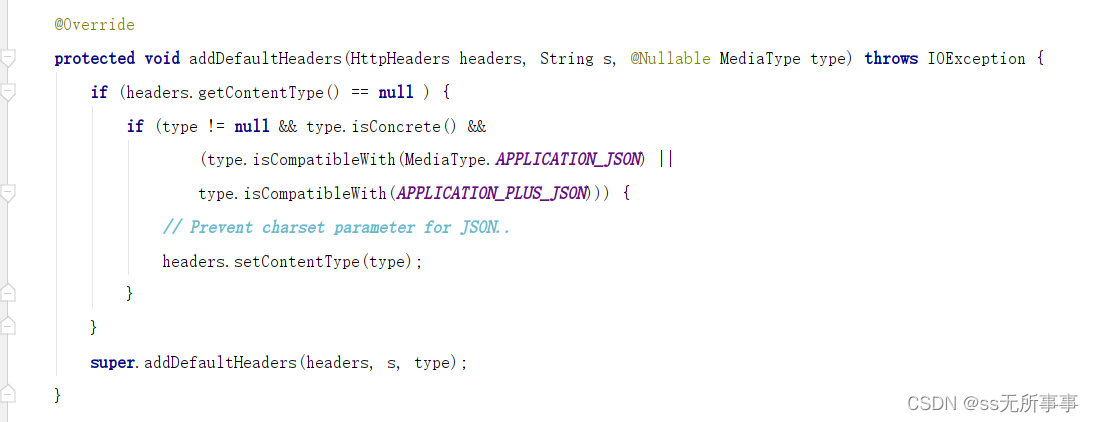
SpringBoot实现统一返回接口(除AOP)
起因 关于使用AOP去实现统一返回接口在之前的博客中我们已经实现了,但我突然突发奇想,SpringBoot中异常类的统一返回好像是通过RestControllerAdvice 这个注解去完成的,那我是否也可以通过这个注解去实现统一返回接口。 正文 这个方法主要…...

ChatGpt - 基于人工智能检索进行论文写作
摘要 ChatGPT 是一款由 OpenAI 训练的大型语言模型,可用于各种自然语言处理任务,包括论文写作。使用 ChatGPT 可以帮助作者提高论文的语言流畅度、增强表达能力和提高文章质量。在写作过程中,作者可以使用 ChatGPT 生成自然语言的段落、句子、单词或者短语,作为启发式的写…...

实例三:MATLAB APP design-多项式函数拟合
一、APP 界面设计展示 注:在左侧点击数据导入,选择自己的数据表,如果数据导入成功,在右侧的空白框就会显示数据导入成功。在多项式项数右侧框中输入项数,例如2、3、4等,点击计算按钮,右侧坐标框就会显示函数图像,在平均相对误差下面的空白框显示平均相对误差。...

springboot多种方式注入bean获取Bean
springboot动态注入bean1、创建Bean(demo)2、动态注入Bean3、通过注解注入Bean4、通过config配置注入Bean5、通过Import注解导入6、使用FactoryBean接口7、实现BeanDefinitionRegistryPostProcessor接口1、创建Bean(demo) Data public class Demo(){private String name;publi…...

Markdown及其语法详细介绍(全面)
文章目录一、基本语法1.标题2.段落和换行3.强调4.列表5.链接6.图片7.引用8.代码9.分割线10表格二、扩展语法1.标题锚点标题 {#anchor}2.脚注3.自动链接4.任务列表5.删除线6.表情符号7.数学公式三、Markdown 应用1.文档编辑2.博客写作3.代码笔记四、常见的工具和平台支持 Markdo…...
在Linux和Windows上安装sentinel-1.8.5
记录:380场景:在CentOS 7.9操作系统上,安装sentinel-1.8.5。在Windows上操作系统上,安装sentinel-1.8.5。Sentinel是面向分布式、多语言异构化服务架构的流量治理组件。版本:JDK 1.8 sentinel-1.8.5 CentOS 7.9官网地址…...
)
面试攻略,Java 基础面试 100 问(十)
StringBuffer、StringBuilder、String区别 线程安全 StringBuffer:线程安全,StringBuilder:线程不安全。 因为 StringBuffer 的所有公开方法都是 synchronized 修饰的,而 StringBuilder 并没有 synchronized 修饰。 StringBuf…...
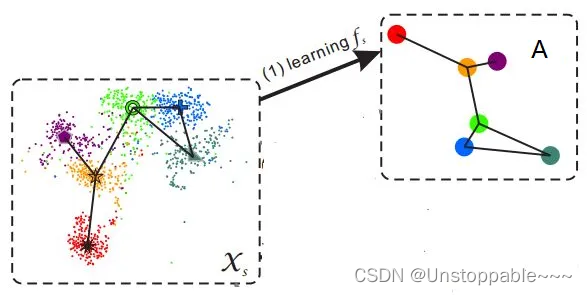
Zero-shot(零次学习)简介
zero-shot基本概念 首先通过一个例子来引入zero-shot的概念。假设我们已知驴子和马的形态特征,又已知老虎和鬣狗都是又相间条纹的动物,熊猫和企鹅是黑白相间的动物,再次的基础上,我们定义斑马是黑白条纹相间的马科动物。不看任何斑…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...
