C语言好题解析(三)
目录
- 选择题一
- 选择题二
- 选择题三
- 选择题四
- 编程题一
- 编程题二
选择题一
以下程序段的输出结果是()
#include<stdio.h>
int main()
{
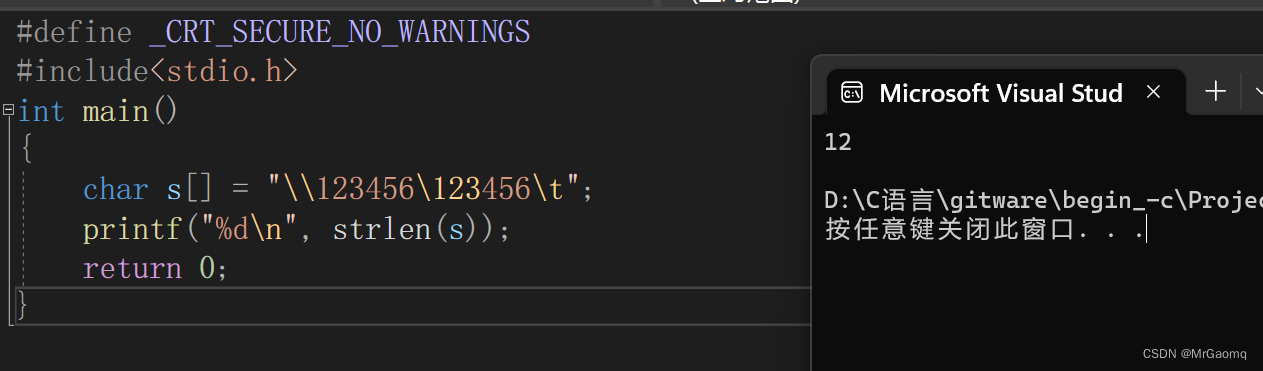
char s[] = "\\123456\123456\t";
printf("%d\n", strlen(s));
return 0;
}
A: 12 B: 13 C: 16 D: 以上都不对
【答案】 A
【分析】这道题涉及到转义字符,\是一种转义字符,而\就是以(第一个\)修饰(第二个\)使(第二个\)不表示转义的意思(这里有点绕)
因此\ \为一个字符,而123456则为6个字符。
对后面的\123456\t来说,\123表示一个字符(\ddd:ddd是表示一个1-3位的八进制数字),而456则表示3个字符,\t表示一个字符。
接下来就是strlen的含义,strlen是计算字符串的长度,直到遇见\0才会停止,因此经过前面的分析,strlen(s)=1+6+1+3+1=12
选择题二
若有以下程序,则运行后的输出结果是()
#include <stdio.h>
#define N 2
#define M N + 1
#define NUM (M + 1) * M / 2
int main()
{
printf("%d\n", NUM);
return 0;
}
A: 4 B: 8 C: 9 D: 6
【答案】 B
【分析】这道题就是替换变量,根据上面的定义我们知道
N=2
M=N+1
NUM=(M+1)*M/2
将等式带入第三表达式即可得出结果。
值得注意的是许多人算出的结果为6,因为他们在算时NUM=(2+1+1)(2+1)/2=6(事实上这道题我也是这样算的)
但是实际上正确的算法为:
NUM=(2+1+1) *2+1/2=8.5
这是因为(M+1)*M的第二个M并没有()因此在计算时不能擅自添加()。
最后的8则是因为%d为int的打印方式,所以将小数点后的5省略了

选择题三
如下函数的 f(1) 的值为( )
int f(int n)
{
static int i = 1;
if(n >= 5)
return n;
n = n + i;
i++;
return f(n);
}
A: 5 B: 6 C: 7 D: 8
【答案】C
【分析】这道题是递归类型的题 ,n>=5为限制条件,但需要注意的是static修饰的i
千万不用以为int i=1,i就一直为1了,static修饰使它可以保留以前变化的值,因此i是一直在增加的
详细的过程如图:


选择题四
下面3段程序代码的效果一样吗( )
int b;
(1)const int *a = &b;
(2)int const *a = &b;
(3)int *const a = &b;
A: (2)=(3) B: (1)=(2) C: 都不一样 D: 都一样
【答案】 B
【分析】我们需要了解const的含义,只要了解了含义就可以做这道题
const是修饰他后面的变量使它的地址或者数值无法改变。
比如:
(1)中const修饰的是a,就说明a无法改变,因为a是表示的地址,所以a所表示的地址无法改变,但是a的值是可以改变的。
(2)中const修饰的仍是*a(和int无关)
(3)const修饰的是a,也就说明a所代表的数值无法改变,但a的地址是可以改变。
编程题一
验证尼科彻斯定理
任何一个整数 m 的立方都可以写成 m 个连续奇数之和
例如
1^3=1
2^3=3+5
3^3=7+9+11
4^3=13+15+17+19
输入一个正整数 m(m≤100)
将 m 的立方写成 m 个连续奇数之和的形式输出。
注意:本题含有多组输入数据。
输入描述:输入一个int整数
输出描述:输出分解后的string
示例:
输入:6
输出:31+33+35+37+39+41
【题目分析】
我们需要用n将m的立方表示出来,然后由连续奇数之和可以设第一个奇数a1=x,然后由等差数列的求和公式可以算出Sm=m*x+(m-1)2,
即可得出关系式m^3=mx+2 * (m-1) * m
即x=m * m- m+1
因为x为第一项,为了求出x的具体值我们需要用到for循环
【代码】
int main()
{int m = 0;scanf("%d", &m);int n = m * m * m;int x = m * m - m + 1;for (int i = 1; i <= m; i++){if (i == m)printf("%d", x);else{printf("%d+", x);x += 2;}}return 0;
}
编程题二
等差数列 2,5,8,11,14, … 。(从 2 开始的 3 为公差的等差数列),求等差数列前 n 项和
注意:本题有多组输入
输入描述:输入一个正整数 n 。
输出描述:输出一个相加后的整数
示例:
输入:2 输入:275
输出:7 输出:113575
说明:2+5=7 说明:2+5+...+821+824=113575
【题目分析】
这道题和上一题的解法类似,但是是求的Sn
因此需要设一个sum(即Sn),还有x通过式子sum+=x,x+=3再加上循环即可解决问题
【代码】
#include<stdio.h>
int main()
{int n, x = 2, sum = 0;scanf("%d", &n);for (int i = 1; i <= n; i++){sum += x;x += 3;}printf("%d", sum);return 0;
}
相关文章:

C语言好题解析(三)
目录 选择题一选择题二选择题三选择题四编程题一编程题二 选择题一 以下程序段的输出结果是()#include<stdio.h> int main() { char s[] "\\123456\123456\t"; printf("%d\n", strlen(s)); return 0; }A: 12 B: 13 …...

OpenCV之remap的使用
OpenCV中使用remap实现图像的重映射。 重映射是指将图像中的某一像素值赋值到指定位置的操作:g(x,y) f ( h(x,y) ), 在这里, g( ) 是目标图像, f() 是源图像, 而h(x,y) 是作用于 (x,y) 的映射方法函数。为了完成映射过程, 需要获得一些插值为…...
leetcode 377. 组合总和 Ⅳ
2023.8.17 本题属于完全背包问题,乍一看和昨天那题 零钱兑换II 类似,但细看题目发现:今天这题是排列问题,而“零钱兑换II”是组合问题。排列问题强调顺序,而组合顺序不强调顺序。 这里先说个结论:先遍历物品…...
C++笔记之花括号和圆括号初始化区别,列表初始化和初始化列表区别
C笔记之花括号和圆括号初始化区别,列表初始化和初始化列表区别 code review! 文章目录 C笔记之花括号和圆括号初始化区别,列表初始化和初始化列表区别1.花括号{}进行初始化和圆括号()进行初始化2.列表初始化(list initialization࿰…...

git报错Add correct host key
想克隆备份的笔记库,失败。 测试连接github报错如下。 $ ssh -T gitgithub.comWARNING: POSSIBLE DNS SPOOFING DETECTED! The RSA host key for github.com has changed, and the key for the corresponding IP address 140.82.121.4 is unknown. This c…...
Kvm配置ovs网桥
环境:部署在kvm虚拟环境上(让虚拟机和宿主机都可以直接从路由器获取到独立ip) 1、安装ovs软件安装包并启动服务(一般采用源码安装,此处用yum安装) yum install openvswitch-2.9.0-3.el7.x86_64.rpm syste…...
AraNet:面向阿拉伯社交媒体的新深度学习工具包
阿拉伯语是互联网上第四大最常用的语言,它在社交媒体上的日益增加为大规模研究阿拉伯语在线社区提供了充足的资源。然而,目前很少有工具可以从这些数据中获得有价值的见解,用于决策、指导政策、协助应对等。这种情况即将改变吗? …...

P13-CNN学习1.3-ResNet(神之一手~)
论文地址:CVPR 2016 Open Access Repository https://arxiv.org/pdf/1512.03385.pdf Abstract 翻译 深层的神经网络越来越难以训练。我们提供了一个残差学习框架用来训练那些非常深的神经网络。我们重新定义了网络的学习方式,让网络可以直接学习输入信息与输出信息…...

【C++】set/multiset容器
1.set基本概念 #include <iostream> using namespace std;//set容器构造和赋值 #include<set>//遍历 void printSet(const set<int>& st) {for (set<int>::const_iterator it st.begin(); it ! st.end(); it){cout << *it << " …...

docker拉取镜像时报错Error response from daemon: Head ““no basic auth credentials
一:场景:新搭建一台服务器,需要拉取公司私有镜像仓库。 docker拉取私有仓库报如下错误: Error response from daemon: Head "" no basic auth credentials 二:解决方式 docker私有仓库需要登录授权,因此…...
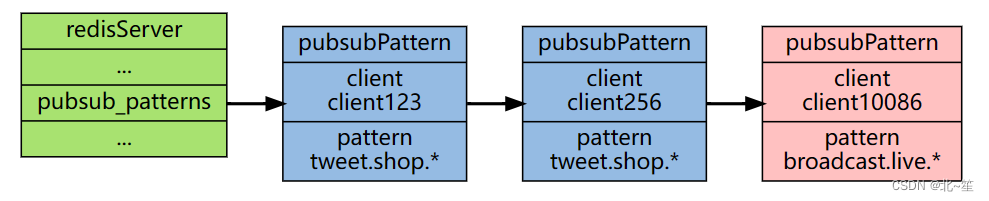
Redis消息传递:发布订阅模式详解
目录 1.Redis发布订阅简介 2.发布/订阅使用 2.1 基于频道(Channel)的发布/订阅 2.2 基于模式(pattern)的发布/订阅 3.深入理解Redis的订阅发布机制 3.1 基于频道(Channel)的发布/订阅如何实现的? 3.2 基于模式(Pattern)的发布/订阅如何实现的? 3.3 Sp…...
- 句柄)
最强自动化测试框架Playwright(36)- 句柄
剧作家可以为页面 DOM 元素或页面内的任何其他对象创建句柄。这些句柄存在于 Playwright 进程中,而实际对象位于浏览器中。有两种类型的句柄: JSHandle 引用页面中的任何 JavaScript 对象ElementHandle 引用页面中的 DOM 元素,它具有额外的方…...
推荐一个绘图平台(可替代Visio)
不废话,简易记网址: draw.io 网站会重定向到:https://app.diagrams.net/...

【探索Linux】—— 强大的命令行工具 P.6(调试器-gdb、项目自动化构建工具-make/Makefile)
阅读导航 前言一、什么是调试器二、详解 GDB - 调试器1.使用前提2.经常使用的命令3.使用小技巧 三、项目自动化构建工具 - make/Makefile1. make命令⭕语法⭕常用选项⭕常用操作⭕make命令的工作原理⭕make命令的优势: 2.Makefile文件⭕Makefile的基本结构⭕Makefil…...
echarts-convert.js使用
echarts-convert.js demo 点击下载 1、本地安装phantom.js插件 window版本下载 2、更改文件路径 (D:\phantomjs-2.1.1-windows\bin)改为本地项目文件路径 3、打开cmd命令行,并格式化语言 运行以下命令 将命令行语言改为中文简体 chcp…...
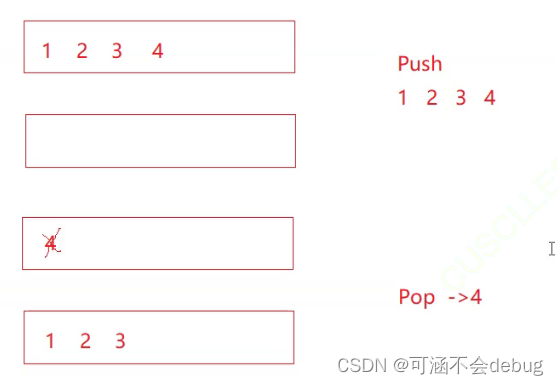
数据结构之队列详解(包含例题)
一、队列的概念 队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操…...
Prometheus的搭建与使用
一、安装Prometheus 官网下载地址:Download | Prometheus 解压:tar -zxvf prometheus-2.19.2.linux-amd64.tar.gz重命名: mv prometheus-2.19.2.linux-amd64 /home/prometheus进入对应目录: cd /home/prometheus查看配置文件&am…...

实战指南,SpringBoot + Mybatis 如何对接多数据源
系列文章目录 MyBatis缓存原理 Mybatis plugin 的使用及原理 MyBatisSpringboot 启动到SQL执行全流程 数据库操作不再困难,MyBatis动态Sql标签解析 从零开始,手把手教你搭建Spring Boot后台工程并说明 Spring框架与SpringBoot的关联与区别 Spring监听器…...
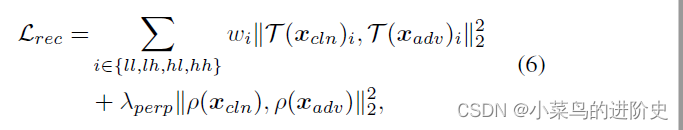
论文阅读——Imperceptible Adversarial Attack via Invertible Neural Networks
Imperceptible Adversarial Attack via Invertible Neural Networks 作者:Zihan Chen, Ziyue Wang, Junjie Huang*, Wentao Zhao, Xiao Liu, Dejian Guan 解决的问题:虽然视觉不可感知性是对抗性示例的理想特性,但传统的对抗性攻击仍然会产…...
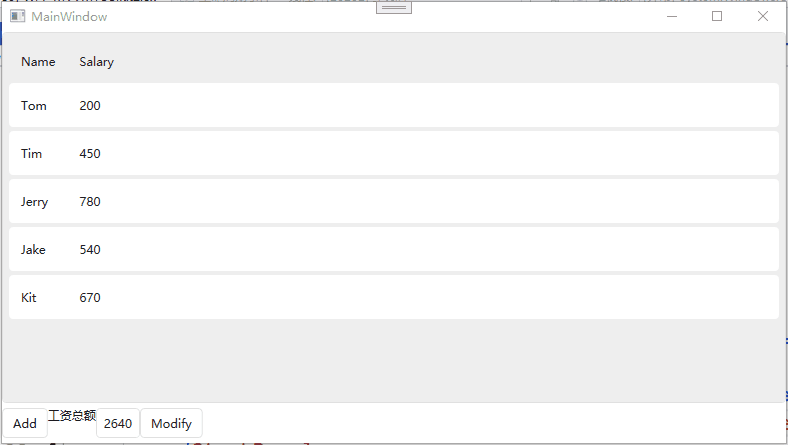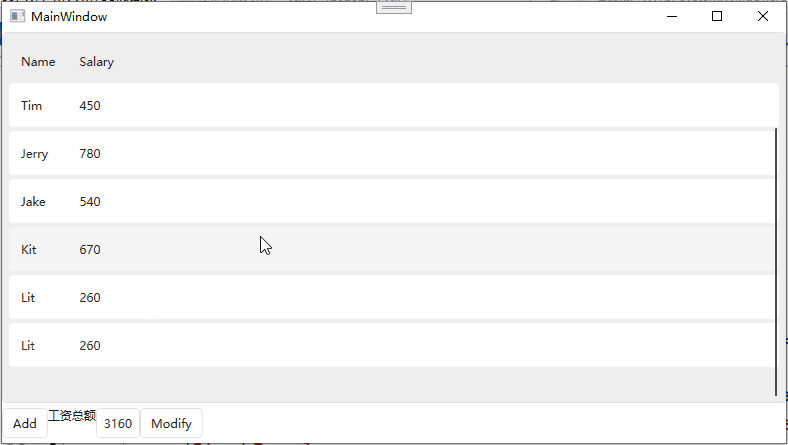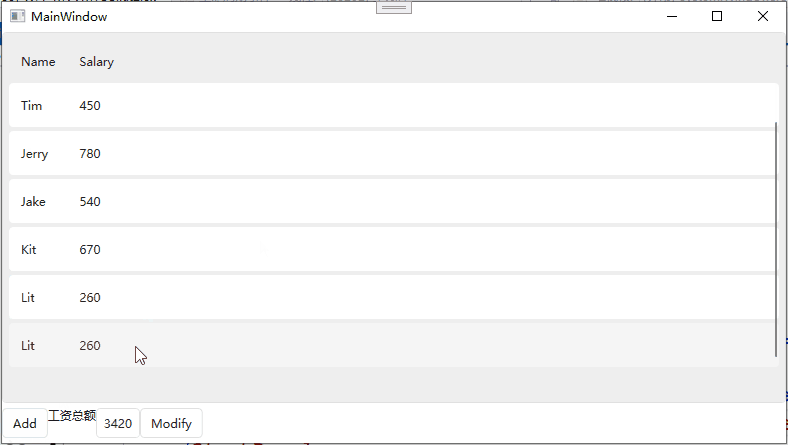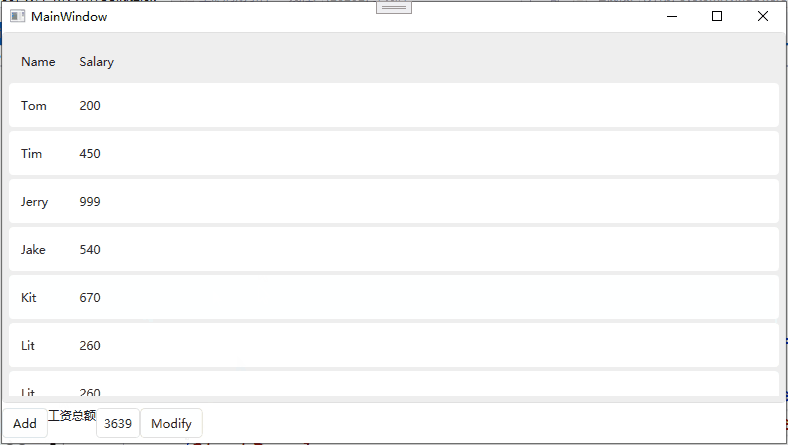
List和ObservableCollection和ListBinding在MVVM模式下的对比
List和ObservableCollection和ListBinding在MVVM模式下的对比 List 当对List进行增删操作后,并不会对View进行通知。 //Employee public class Employee : INotifyPropertyChanged {public event PropertyChangedEventHandler? PropertyChanged;public string N…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...

车载诊断架构 --- ZEVonUDS(J1979-3)简介第一篇
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从,不跟风。把自己的精力全部用在自己。一是去掉多余,凡事找规律,基础是诚信;二是…...

shell脚本质数判断
shell脚本质数判断 shell输入一个正整数,判断是否为质数(素数)shell求1-100内的质数shell求给定数组输出其中的质数 shell输入一个正整数,判断是否为质数(素数) 思路: 1:1 2:1 2 3:1 2 3 4:1 2 3 4 5:1 2 3 4 5-------> 3:2 4:2 3 5:2 3…...

ubuntu中安装conda的后遗症
缘由: 在编译rk3588的sdk时,遇到编译buildroot失败,提示如下: 提示缺失expect,但是实测相关工具是在的,如下显示: 然后查找借助各个ai工具,重新安装相关的工具,依然无解。 解决&am…...

若依项目部署--传统架构--未完待续
若依项目介绍 项目源码获取 #Git工具下载 dnf -y install git #若依项目获取 git clone https://gitee.com/y_project/RuoYi-Vue.git项目背景 随着企业信息化需求的增加,传统开发模式存在效率低,重复劳动多等问题。若依项目通过整合主流技术框架&…...

React、Git、计网、发展趋势等内容——前端面试宝典(字节、小红书和美团)
React React Hook实现架构、.Hook不能在循环嵌套语句中使用 , 为什么,Fiber架构,面试向面试官介绍,详细解释 用户: React Hook实现架构、.Hook不能在循环嵌套语句中使用 , 为什么,Fiber架构,面试向面试官介绍&#x…...
