算法训练营 day49 动态规划 爬楼梯 (进阶)零钱兑换 完全平方数
算法训练营 day49 动态规划 爬楼梯 (进阶)零钱兑换 完全平方数
爬楼梯 (进阶)
70. 爬楼梯 - 力扣(LeetCode)
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
改为:一步一个台阶,两个台阶,三个台阶,…,直到 m个台阶。问有多少种不同的方法可以爬到楼顶呢?
1阶,2阶,… m阶就是物品,楼顶就是背包。
每一阶可以重复使用,例如跳了1阶,还可以继续跳1阶。
问跳到楼顶有几种方法其实就是问装满背包有几种方法。
此时大家应该发现这就是一个完全背包问题了!
-
确定dp数组以及下标的含义
dp[i]:爬到有i个台阶的楼顶,有dp[i]种方法。
-
确定递推公式
本题呢,dp[i]有几种来源,dp[i - 1],dp[i - 2],dp[i - 3] 等等,即:dp[i - j]
那么递推公式为:dp[i] += dp[i - j]
-
dp数组如何初始化
既然递归公式是 dp[i] += dp[i - j],那么dp[0] 一定为1,dp[0]是递归中一切数值的基础所在,如果dp[0]是0的话,其他数值都是0了。
-
确定遍历顺序
这是背包里求排列问题,即:1、2 步 和 2、1 步都是上三个台阶,但是这两种方法不一样!
所以需将target放在外循环,将nums放在内循环。
每一步可以走多次,这是完全背包,内循环需要从前向后遍历。
-
举例来推导dp数组
class Solution {public int climbStairs(int n) {int[] dp = new int[n+1];dp[0] = 1;for (int i = 0; i <=n; i++) {for (int j = 1; j <=2; j++) {if(i>=j) dp[i]+=dp[i-j];}}return dp[n];}
}
零钱兑换
322. 零钱兑换 - 力扣(LeetCode)
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
-
确定dp数组以及下标的含义
dp[j]:凑足总额为j所需钱币的最少个数为dp[j]
-
确定递推公式
凑足总额为j - coins[i]的最少个数为dp[j - coins[i]],那么只需要加上一个钱币coins[i]即dp[j - coins[i]] + 1就是dp[j](考虑coins[i])
所以dp[j] 要取所有 dp[j - coins[i]] + 1 中最小的。
递推公式:dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
-
dp数组初始化
首先凑足总金额为0所需钱币的个数一定是0,那么dp[0] = 0;
其他下标对应的数值呢?
考虑到递推公式的特性,dp[j]必须初始化为一个最大的数,否则就会在min(dp[j - coins[i]] + 1, dp[j])比较的过程中被初始值覆盖。所以下标非0的元素都是应该是最大值。
-
确定遍历顺序
本题求钱币最小个数,那么钱币有顺序和没有顺序都可以,都不影响钱币的最小个数。
-
举例推导dp数组
以输入:coins = [1, 2, 5], amount = 5为例

dp[amount]为最终结果。
class Solution {public int coinChange(int[] coins, int amount) {int max = amount + 1;int[] dp = new int[amount + 1];Arrays.fill(dp, max);dp[0] = 0;for (int i = 0; i < coins.length; i++) {for (int j = coins[i]; j <= amount; j++) {if (dp[j - coins[i]] != max) {dp[j] = Math.min(dp[j - coins[i]] + 1, dp[j]);}}}return dp[amount] == max ? -1 : dp[amount];}
}
完全平方数
279. 完全平方数 - 力扣(LeetCode)
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
-
确定dp数组(dp table)以及下标的含义
dp[j]:和为j的完全平方数的最少数量为dp[j]
-
定递推公式
dp[j] 可以由dp[j - i * i]推出, dp[j - i * i] + 1 便可以凑成dp[j]。
此时我们要选择最小的dp[j],所以递推公式:dp[j] = min(dp[j - i * i] + 1, dp[j]);
-
dp数组如何初始化
dp[0]表示 和为0的完全平方数的最小数量,那么dp[0]一定是0。
非0下标的dp[j]应该是多少呢?
从递归公式dp[j] = min(dp[j - i * i] + 1, dp[j]);中可以看出每次dp[j]都要选最小的,所以非0下标的dp[j]一定要初始为最大值,这样dp[j]在递推的时候才不会被初始值覆盖。
-
确定遍历顺序
本题外层for遍历背包,内层for遍历物品,还是外层for遍历物品,内层for遍历背包,都是可以的!
-
举例推导dp数组
已输入n为5例,dp状态图如下:

class Solution {public int numSquares(int n) {int max = n+1;int[] dp = new int[n+1];Arrays.fill(dp,max);dp[0]= 0 ;for (int i=0;i*i<=n;i++){for (int j = i*i; j <=n; j++) {if (dp[j-i*i]!=max)dp[j] = Math.min(dp[j-i*i]+1,dp[j]);}}return dp[n];}
}
相关文章:

算法训练营 day49 动态规划 爬楼梯 (进阶)零钱兑换 完全平方数
算法训练营 day49 动态规划 爬楼梯 (进阶)零钱兑换 完全平方数 爬楼梯 (进阶) 70. 爬楼梯 - 力扣(LeetCode) 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同…...

Vue:extends继承组件复用性
提到extends继承,最先想到的可能是ES6中的class、TS中的interface、面向对象编程语言中中的类和接口概念等等,但是我们今天的关注点在于:如何在Vue中使用extends继承特性。 目录 Vue:创建Vue实例的方式 构造函数方式࿱…...

ChatGPT 的一些思考
最近 ChatGPT3.5 在全世界范围内掀起了一次 AI 的潮流,ChatGPT1.0/ChatGPT2.0 当时也是比较火爆,但是那个当时感觉还是比较初级的应用,相当于是一个进阶版的微软小冰,给人的感觉是有一点智能,但不多。其实从早期版本开…...
GEE学习笔记 六十九:【GEE之Python版教程三】Python基础编程一
环境配置完成后,那么可以开始正式讲解编程知识。之前我在文章中也讲过,GEE的python版接口它是依赖python语言的。目前很多小伙伴是刚开始学习GEE编程,之前或者没有编程基础,或者是没有学习过python。为了照顾这批小伙伴࿰…...
大数据全系安装
内容版本号CentOS7.6.1810ZooKeeper3.4.6Hadoop2.9.1HBase1.2.0MySQL5.6.51HIVE2.3.7Sqoop1.4.6flume1.9.0kafka2.8.1scala2.12davinci3.0.1spark2.4.8flink1.13.5 1. 下载CentOS 7镜像 CentOS官网 2. 安装CentOS 7系统——采用虚拟机方式 2.1 新建虚拟机 2.2.1 [依次选择]-&…...

stable-diffusion-webui 安装使用
文章目录1.github 下载,按教程运行2.安装python 忘记勾选加入环境变量,自行加入(重启生效)3.环境变量添加后,清理tmp ,venv重新运行4.运行报错,无法升级pip,无法下载包,5…...

3D点云处理:点云聚类--FEC: Fast Euclidean Clustering for Point Cloud Segmentation
文章目录 聚类结果一、论文内容1.1 Ground Surface Removal1.2 Fast Euclidean Clustering题外:欧几里得聚类Fast Euclidean Clustering二、参考聚类结果 原始代码中采用的是pcl中的搜索方式,替换为另外第三方库,速度得到进一步提升。 一、论文内容 论文中给出的结论:该…...
| 代码+思路+重要知识点)
华为OD机试题 - 射击比赛(JavaScript)| 代码+思路+重要知识点
最近更新的博客 华为OD机试题 - 括号检查(JavaScript) 华为OD机试题 - 最小施肥机能效(JavaScript) 华为OD机试题 - 子序列长度(JavaScript) 华为OD机试题 - 众数和中位数(JavaScript) 华为OD机试题 - 服务依赖(JavaScript) 华为OD机试题 - 字符串加密(JavaScript)…...
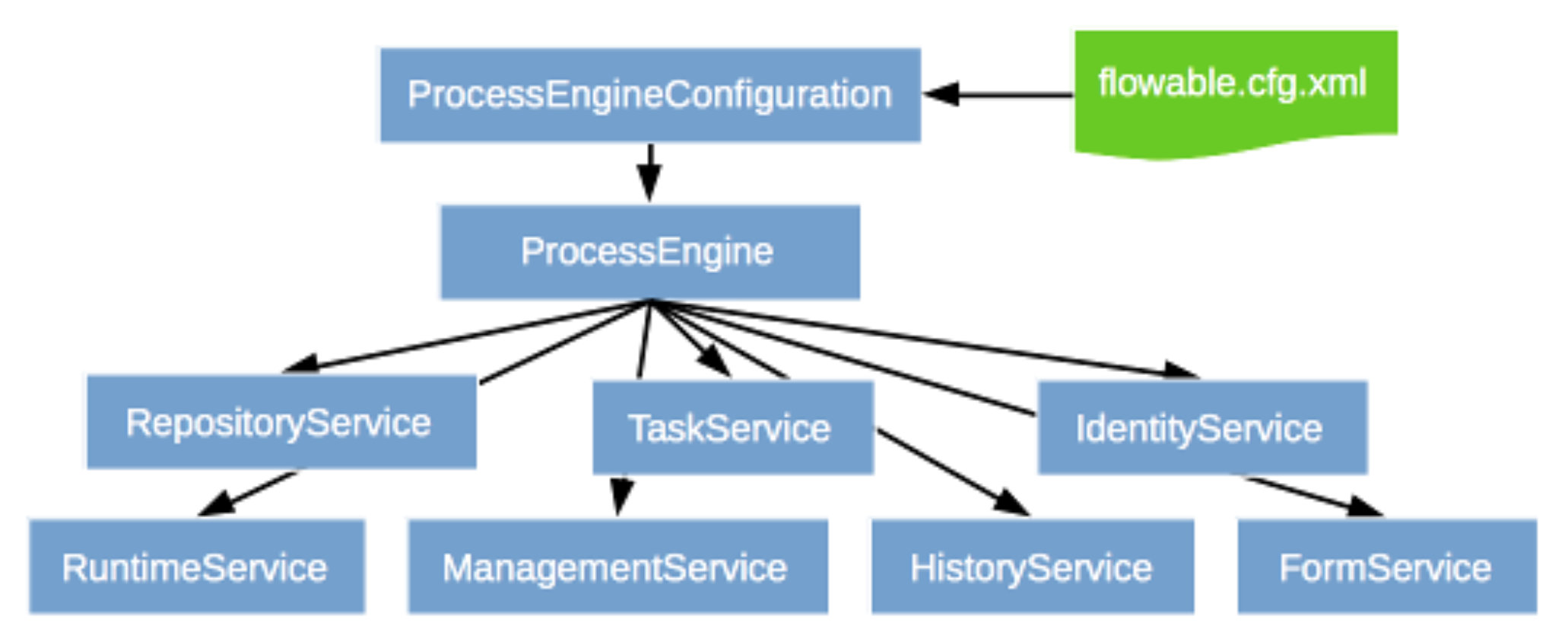
流程引擎之Flowable简介
背景Flowable 是一个流行的轻量级的采用 Java 开发的业务流程引擎,通过 Flowable 流程引擎,我们可以部署遵循 BPMN2.0 协议的流程定义(一般为XML文件)文件,并能创建流程实例,查询和访问流程相关的实例与数据…...
AcWing:4861. 构造数列、4862. 浇花(C++)
目录 4861. 构造数列 问题描述: 实现代码: 4862. 浇花 问题描述: 实现代码: 4861. 构造数列 问题描述: 我们规定如果一个正整数满足除最高位外其它所有数位均为 00,则称该正整数为圆数。 例如&…...
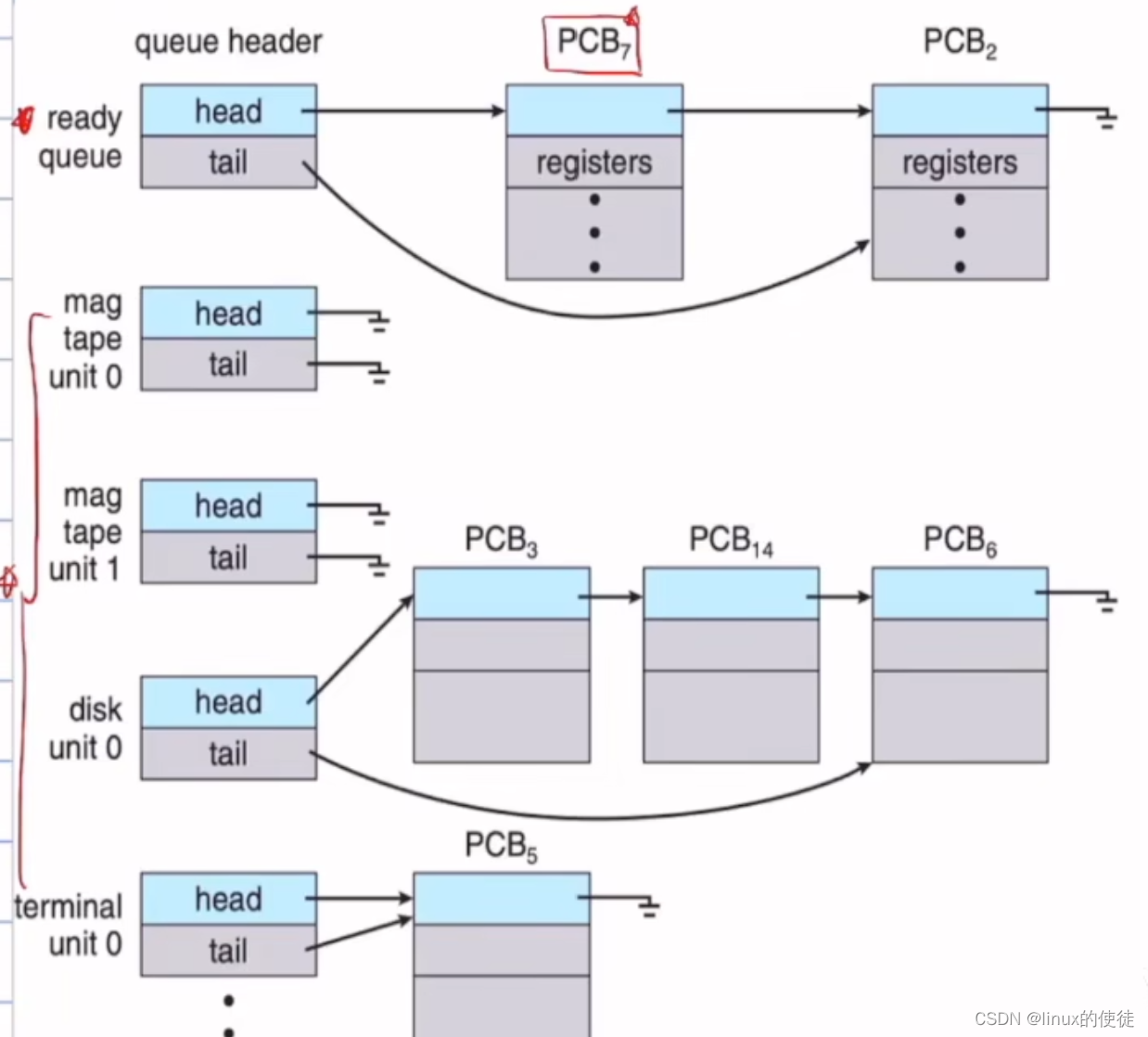
进程的概念
进程的概念 程序的概念 这里说的是一个可执行文件,passive的意思可以理解为我们这个执行文件需要我们进行双击才会被被执行。 双击后,程序入口地址读入寄存器,程序加载入主存,成为一个进程 进程是主动去获取想要的资源࿰…...
自动化测试5年经验,分享一些心得
自动化测试介绍 自动化测试(Automated Testing),是指把以人为驱动的测试行为转化为机器执行的过程。实际上自动化测试往往通过一些测试工具或框架,编写自动化测试用例,来模拟手工测试过程。比如说,在项目迭代过程中,持…...
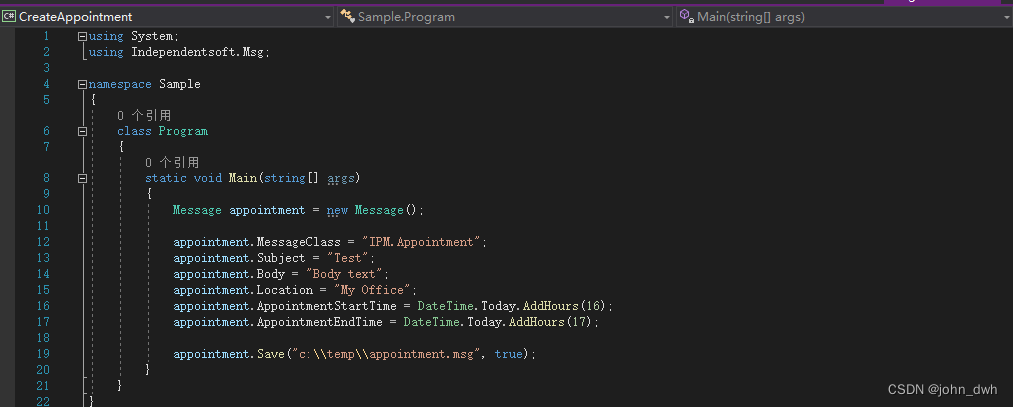
independentsoft.de/MSG .NET Framework Crack
MSG .NET 是用于 .NET Framework / .NET Core 的 Microsoft Outlook .msg 文件 API。API 允许您轻松创建/读取/解析/转换 .msg 文件等。API 不需要在机器上安装 Microsoft Outlook 或任何其他第三方应用程序或库即可工作。 以下示例向您展示了如何打开现有文件并显示消息的某些…...

基于Transformer的NLP处理管线
HuggingFace transformers 是一个整合了跨语言、视觉、音频和多模式模态与最先进的预训练模型并且提供用户友好的 API 的AI开发库。 它由 170 多个预训练模型组成,支持 PyTorch、TensorFlow 和 JAX 等框架,能够在代码之间进行互操作。 这个库还易于部署&…...
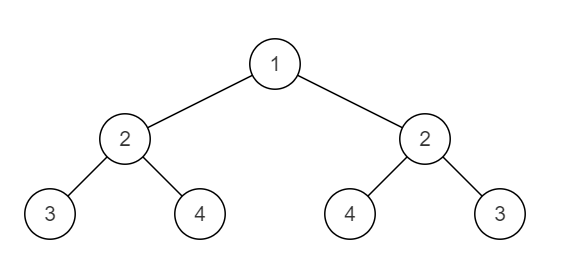
二叉树OJ(一)二叉树的最大深度 二叉搜索树与双向链表 对称的二叉树
二叉树的最大深度 二叉树中和为某一值的路径(一) 二叉搜索树与双向链表 对称的二叉树 二叉树的最大深度 描述 求给定二叉树的最大深度, 深度是指树的根节点到任一叶子节点路径上节点的数量。 最大深度是所有叶子节点的深度的最大值。 (注:…...

使用Fairseq进行Bart预训练
文章目录前言环境流程介绍数据部分分词部分预处理部分训练部分遇到的问题问题1可能遇到的问题问题1问题2前言 本文是使用 fairseq 做 Bart 预训练任务的踩坑记录huggingface没有提供 Bart 预训练的代码 facebookresearch/fairseq: Facebook AI Research Sequence-to-Sequence…...
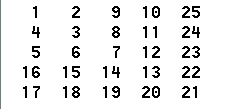
n阶数字回转方阵 ← 模拟法
【问题描述】 请编程输出如下数字回旋方阵。 【算法代码】 #include <bits/stdc.h> using namespace std;const int maxn100; int z[maxn][maxn];void matrix(int n) {int num2;z[0][0]1;int i0,j1;while(i<n && j<n) {while(i<j) z[i][j]num;while(j&…...

【人工智能AI】二、NoSQL 基础知识《NoSQL 企业级基础入门与进阶实战》
写一篇介绍 NoSQL 基础知识的技术文章,分5个章节,每个章节细分到3级目录,重点介绍一下NoSQL 数据模型,NoSQL 数据库架构,NoSQL 数据库特性等,不少于2000字。 NoSQL 基础知识 NoSQL(Not Only SQ…...

Camera Rolling Shutter和Global Shutter的区别
卷帘快门(Rolling Shutter)与全局快门(Global Shutter)的区别 什么是快门 快门是照相机用来控制感光片有效曝光时间的机构。 快门是照相机的一个重要组成部分,它的结构、形式及功能是衡量照相机档次的一个重要因素。 …...

模版之AnyType
title: 模版之AnyType date: 2023-02-19 21:49:53 permalink: /pages/54a0bf/ categories: 通用领域编程语言C tags:C元编程 author: name: zhengzhibing link: https://azmddy.top/pages/54a0bf/ 模版之AnyType 在研究C的编译期反射时,发现了AnyType很有意思。 首…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...
