2023 年牛客多校第十场题解
C Multiplication
题意:定义 k k k-shift 数是满足 k x y ‾ = y x ‾ k\overline{xy}=\overline{yx} kxy=yx 的数字。给定 k k k,求最大不超过 n n n 的 k k k-shift 数。 1 ≤ n ≤ 1 0 100 1 \le n \le 10^{100} 1≤n≤10100, 2 ≤ k ≤ 9 2 \le k \le 9 2≤k≤9。
解法:设 f ( x ) f(x) f(x) 表示 x x x 十进制下的位数。考虑 k k k-shift 数字的定义,假设这个数字的高位为 x x x,低位为 y y y,乘以 k k k 后发生了交换,则有:
k ( x × 1 0 f ( y ) + y ) = y × 1 0 f ( x ) + x k(x\times 10^{f(y)}+y)=y\times 10^{f(x)}+x k(x×10f(y)+y)=y×10f(x)+x
考虑分离 x , y x,y x,y:
( k × 1 0 f ( y ) − 1 ) x = ( 1 0 f ( x ) − k ) y (k\times 10^{f(y)}-1)x=(10^{f(x)}-k)y (k×10f(y)−1)x=(10f(x)−k)y
即
x y = 1 0 f ( x ) − k k × 1 0 f ( y ) − 1 \dfrac{x}{y}=\dfrac{10^{f(x)}-k}{k\times 10^{f(y)}-1} yx=k×10f(y)−110f(x)−k
这时考虑到数字位数不大,可以枚举 f ( x ) , f ( y ) f(x),f(y) f(x),f(y),则右边确定。考虑计算它的 gcd \gcd gcd 并进行分式约简,得 1 0 f ( x ) − k k × 1 0 f ( y ) − 1 = p q \dfrac{10^{f(x)}-k}{k\times 10^{f(y)}-1}=\dfrac{p}{q} k×10f(y)−110f(x)−k=qp,这时真正的 x y \dfrac{x}{y} yx 应为 k p k q \dfrac{kp}{kq} kqkp。注意 x , y x,y x,y 由数字长度 f ( x ) , f ( y ) f(x),f(y) f(x),f(y) 和上界的约束,可以得到 k k k 的数字范围。这时就可以快速统计出当前状态下最大的 k k k 即可。
def gcd(a, b):return a if b == 0 else gcd(b, a % b)n, k, ans = int(input()), int(input()), 0
L = len(str(n))
p = [10**i for i in range(L + 1)]
for i in range(1, L):for j in range(1, L - i + 1):x, y = 10**i - k, k * 10**j - 1z = gcd(x, y)x, y = x // z, y // zl = max((p[i - 1] + x - 1) // x, (p[j - 1] + y - 1) // y)r = min((p[i] - 1) // x, (p[j] - 1) // y, n // (x * p[j] + y))if l > r:continueans = max(ans, r * (x * p[j] + y))
print(ans)D Agnej
题意:有个 n + 1 n+1 n+1 层的木塔,每层原本由 m m m 根木头构成。现在除了最顶层是满的 m m m 根木头,其余每层有些木头已经被抽走了。先后手轮流从非顶层抽走一根木头,如果一层中最左侧或最右侧 ⌈ m 2 ⌉ \left \lceil \dfrac{m}{2}\right \rceil ⌈2m⌉ 根木头都被抽走,则木塔倒塌。谁让木塔倒塌谁输,问胜负。 1 ≤ n × m ≤ 1 0 5 1 \le n\times m \le 10^5 1≤n×m≤105。
解法:显然每层独立,因而考虑计算每层答案的 SG 值再异或起来。SG 值的求法是枚举所有的可行后继状态,然后求这些后继状态 v v v 的 SG 值,当前状态 u u u 的 SG 值为 m e x { S G ( v ) } {\rm mex}\{{\rm SG}(v)\} mex{SG(v)}。
首先考虑 m m m 为偶数的情况。定义 ( l , r ) (l,r) (l,r) 表示左边有 l l l 根木头右边有 r r r 根木头的状态。这时不存在中间的支撑,两边中如果有一半如果抽完就会倒。显然边界情况 ( 1 , 1 ) (1,1) (1,1) 即左右各有一个木头显然是先手必败的,即 S G ( 1 , 1 ) = 0 {\rm SG(1,1)=0} SG(1,1)=0,而且唯一不能操作的状态仅此一个。考虑面对总共偶数根木头时,即 l + r l+r l+r 为偶数。先手无论抽什么,后手都面对的是奇数根木头,一定不会是必败态。因而 l + r l+r l+r 为奇数时 S G = 1 {\rm SG}=1 SG=1,反之为 0 0 0。因而 S G ( l , r ) = ( l + r ) m o d 2 {\rm SG}(l,r)=(l+r) \bmod 2 SG(l,r)=(l+r)mod2。
m m m 为奇数时,中间可能存在一根木头。设此时状态为 ( l , m , r ) (l,m,r) (l,m,r) 表示左、中、右的木头个数,其中 m ∈ [ 0 , 1 ] m \in [0,1] m∈[0,1]。如果正中间不存在木头,则退化到偶数情况。如果中间存在木头,再考虑两类情况:
- 单侧无木头,即形如 ( 0 , 1 , r ) (0,1,r) (0,1,r) 状态。此时只能依次抽取右侧的木头, S G ( 0 , 1 , r ) = r m o d 2 {\rm SG}(0,1,r)=r \bmod 2 SG(0,1,r)=rmod2。
- 形如 ( 1 , 1 , r ) (1,1,r) (1,1,r) 状态。则它可以转移到的状态有 ( 1 , 1 , r − 1 ) (1,1,r-1) (1,1,r−1), ( 0 , 1 , r ) (0,1,r) (0,1,r), ( 1 , 0 , r ) (1,0,r) (1,0,r)。后两种显然一定是 r m o d 2 r \bmod 2 rmod2 和 ( r + 1 ) m o d 2 (r+1) \bmod 2 (r+1)mod2 即一个为 0 0 0 一个为 1 1 1,因而当前状态的 m e x \rm mex mex 至少为 2 2 2。考虑从 r = 1 r=1 r=1 的边界条件进行讨论( S G ( 1 , 1 , 1 ) = 2 {\rm SG}(1,1,1)=2 SG(1,1,1)=2),不难得到 S G ( 1 , 1 , r ) = 2 + ( r + 1 ) m o d 2 {\rm SG}(1,1,r)=2+(r+1) \bmod 2 SG(1,1,r)=2+(r+1)mod2。
- 一般状态 ( l , 1 , r ) (l,1,r) (l,1,r)。考虑它的边界 ( 2 , 1 , r ) (2,1,r) (2,1,r),有后继状态 ( 1 , 1 , r ) (1,1,r) (1,1,r), ( 2 , 0 , r ) (2,0,r) (2,0,r), ( 2 , 1 , r − 1 ) (2,1,r-1) (2,1,r−1)。不难注意到第一个状态的 SG 大于等于 2 2 2,而第二个状态的 SG 值为 0 0 0 或 1 1 1。这时考虑对 r r r 做归纳,当 r = 1 r=1 r=1 时 ( 2 , 1 , 1 ) (2,1,1) (2,1,1) 的 SG 为 3 3 3,因而 ( 2 , 1 , 2 ) (2,1,2) (2,1,2) 的 SG 为 1 1 1,恰好与 ( 2 , 0 , 3 ) (2,0,3) (2,0,3) 的 SG 相同。因而不难归纳得到 ( 2 , 1 , r − 1 ) (2,1,r-1) (2,1,r−1) 的 SG 始终与 ( 2 , 0 , r ) (2,0,r) (2,0,r) 相同,因而 ( 2 , 1 , r ) (2,1,r) (2,1,r) 的 SG 值只会是 0 , 1 0,1 0,1 交替。这时再对 l l l 归纳可以得到 S G ( l , 1 , r ) = ( l + 1 + r ) m o d 2 {\rm SG}(l,1,r)=(l+1+r) \bmod 2 SG(l,1,r)=(l+1+r)mod2。
#include <bits/stdc++.h>
#define fp(i, a, b) for (int i = a, i##_ = b; i <= i##_; ++i)
#define fd(i, a, b) for (int i = a, i##_ = b; i >= i##_; --i)using namespace std;
using ll = long long;
const int N = 1e5 + 5;
int n, m; char s[N];
int sg(int a, int b, int c) {if (a > b) swap(a, b);if (!c)return (a + b) & 1;else {switch (a) {case 0: return b & 1;case 1: return b & 1 ? 2 : 3;default: return (a + b + 1) & 1;}}
}
void Solve() {scanf("%d%d", &n, &m);int f = 0, k = m & 1 ? m / 2 + 1 : 0;fp(i, 1, n) {scanf("%s", s + 1);int a = 0, b = 0, c = s[k] == '1';fp(j, 1, m / 2) a += s[j] == '1';fp(j, 1, m / 2) b += s[m - j + 1] == '1';f ^= sg(a, b, c);}puts(f ? "Alice" : "Bob");
}
int main() {int t = 1;while (t--) Solve();return 0;
}
F IUPC
题意:一场时长为 t t t 分钟的比赛有 n n n 道题,每个题有最早过题时间的约束,并且一分钟内至多只能交一题,任意 k k k 分钟内只能至多交 m m m 题,问比赛 AK 的方案数。 1 ≤ t ≤ 300 1 \le t \le 300 1≤t≤300, 1 ≤ n ≤ 13 1 \le n \le 13 1≤n≤13, 1 ≤ m ≤ k ≤ 10 1 \le m \le k \le 10 1≤m≤k≤10。
解法:由于要维护前 k k k 时刻做了不超过 m m m 题,并且 k k k 很小,因而比较简单的维护方法就是维护前 k k k 时刻哪些时刻做了题。
考虑维护 f ( i , j , S ) f(i,j,S) f(i,j,S) 表示前 i i i 分钟已经通过 j j j 题,最后 k k k 分钟内过题时刻状态为 S S S 的方案数。 S S S 状态中将第 i i i 分钟的过题状态放在第 k k k 位,而第 i − k + 1 i-k+1 i−k+1 分钟的状态放在最低位。这样当 i ← i + 1 i \leftarrow i+1 i←i+1 时 S S S 只需要先右移一位,然后再在最高位上加入当前这一新的分钟是不是过了题的状态即可。
那么当前是否过题有两种情况:
- 当前时刻不过题。之前所有状态直接原封不动的移动到现在的状态即可。
- 当前时刻过题。那么首先新状态需要满足 ∣ S ∣ ≤ k |S| \le k ∣S∣≤k,再考虑当前这一分钟可以过(a)已经有人过的题(b)已经过了的题不能再交。因而对于 f i , j , S f_{i,j,S} fi,j,S,可行的新过题种类数为 a i − ( j − 1 ) a_i-(j-1) ai−(j−1),此处 a i a_i ai 表示 i i i 时刻以前已经有人过的题目数量。之所以不用考虑题目的顺序是因为当目前已经到达 i i i 时刻,之前所有过的题就都可以纳入考虑,可以将很早就有人过的题憋到现在才交。唯一对选法有影响的只有已经过的题目数量。
因而根据上面两种情况进行转移即可。复杂度 O ( n t 2 k ) \mathcal O(nt2^k) O(nt2k)。
#include <bits/stdc++.h>
#define fp(i, a, b) for (int i = a, i##_ = b; i <= i##_; ++i)
#define fd(i, a, b) for (int i = a, i##_ = b; i >= i##_; --i)using namespace std;
using ll = long long;
const int N = 300 + 5, P = 1e9 + 7;
int n, m, K, T, a[N], f[2][14][1 << 10];
#define inc(a, b) (((a) += (b)) >= P ? (a) -= P : 0)
void Solve() {scanf("%d%d%d%d", &n, &m, &T, &K);for (int x, i = 0; i < n; ++i) scanf("%d", &x), ++a[x];fp(i, 1, m) a[i] += a[i - 1];f[0][0][0] = 1;int p = 0, all = (1 << T) - 1;fp(i, 1, m) {p ^= 1, memset(f[p], 0, sizeof f[p]);fp(j, 0, a[i - 1]) {fp(s, 0, all) {inc(f[p][j][s >> 1], f[p ^ 1][j][s]);int ns = (s >> 1) | (1 << (T - 1));if (j < a[i] && __builtin_popcount(ns) <= K)inc(f[p][j + 1][ns], (ll)(a[i] - j) * f[p ^ 1][j][s] % P);}}}int ans = 0;fp(i, 0, all) inc(ans, f[p][n][i]);printf("%d\n", ans);
}
int main() {int t = 1;// scanf("%d", &t);while (t--) Solve();return 0;
}
H Differential Equation
题意:定义 F 0 ( x ) = x F_0(x)=x F0(x)=x, F i ( x ) = ( x 2 − 1 ) F i − 1 ′ ( x ) F_{i}(x)=(x^2-1)F_{i-1}'(x) Fi(x)=(x2−1)Fi−1′(x)。给定 x 0 x_0 x0 和 n n n,求 F n ( x 0 ) m o d 998 244 353 F_{n}(x_0) \bmod 998\ 244\ 353 Fn(x0)mod998 244 353。 1 ≤ x 0 < 998 244 353 1 \le x_0 <998\ 244\ 353 1≤x0<998 244 353, 0 ≤ n ≤ 2 × 1 0 5 0 \le n \le 2\times 10^5 0≤n≤2×105。
解法:
法一:首先特判 n = 0 n=0 n=0 的答案为 x 0 x_0 x0。下面都考虑 n ≥ 1 n \ge 1 n≥1 的情况。
首先由 F n ( x ) = ( x 2 − 1 ) F n − 1 ′ ( x ) F_n(x)=(x^2-1)F_{n-1}'(x) Fn(x)=(x2−1)Fn−1′(x) 考虑莱布尼兹公式(高阶导数公式),注意到 x 2 − 1 x^2-1 x2−1 在三阶导以上为 0 0 0,因而当 k ≥ 2 k \ge 2 k≥2 时有:
F n ( k ) ( x 0 ) = k ( k − 1 ) F n − 1 ( k − 1 ) ( x 0 ) + 2 x 0 k F n − 1 ( k ) ( x 0 ) + ( x 0 2 − 1 ) F n − 1 ( k + 1 ) ( x 0 ) F_n^{(k)}(x_0)=k(k-1)F_{n-1}^{(k-1)}(x_0)+2x_0kF_{n-1}^{(k)}(x_0)+(x_0^2-1)F_{n-1}^{(k+1)}(x_0) Fn(k)(x0)=k(k−1)Fn−1(k−1)(x0)+2x0kFn−1(k)(x0)+(x02−1)Fn−1(k+1)(x0)
一个最朴素的想法是,代求式 F n ( 0 ) ( x 0 ) F_n^{(0)}(x_0) Fn(0)(x0) 需要 F n − 1 ( 1 ) ( x 0 ) F_{n-1}^{(1)}(x_0) Fn−1(1)(x0)(注意此时的边界条件),然后 F n − 1 ( 1 ) ( x 0 ) F_{n-1}^{(1)}(x_0) Fn−1(1)(x0) 又需要 F n − 2 ( 2 ) ( x 0 ) F_{n-2}^{(2)}(x_0) Fn−2(2)(x0) 等若干阶导数,依次类推。因而我们需要 F i ( j ) ( x 0 ) F_{i}^{(j)}(x_0) Fi(j)(x0) 即任意一个函数的任意阶导数。这是因为上式中 k k k 阶导推导出了 k + 1 k+1 k+1 阶导,一项推出了三项。而直接递推显然是不太可行的。
这时由于目标函数 F n ( x ) F_n(x) Fn(x) 必然为一多项式函数(更加具体的,一定是一个 n + 1 n+1 n+1 次多项式),因而一定可以由泰勒展开得到:
F n ( x 0 ) = ∑ i = 0 n + 1 F n ( i ) ( x 1 ) i ! ( x 0 − x 1 ) i F_n(x_0)=\sum_{i=0}^{n+1}\dfrac{F_{n}^{(i)}(x_1)}{i!}(x_0-x_1)^i Fn(x0)=i=0∑n+1i!Fn(i)(x1)(x0−x1)i
因而这提示我们可以考虑不用求 x 0 x_0 x0 处的任意多阶导数,而转而求一些特殊点的导数。观察原递推式,不难发现当递推式中的 x 0 = 1 x_0=1 x0=1 时,一项可以只递推出两项。因而考虑这个特殊情况,即我们可以令 x 1 = 1 x_1=1 x1=1,那么原式转化为
F n ( x 0 ) = ∑ i = 0 n + 1 F n ( i ) ( 1 ) i ! ( x 0 − 1 ) i F_n(x_0)=\sum_{i=0}^{n+1}\dfrac{F_{n}^{(i)}(1)}{i!}(x_0-1)^i Fn(x0)=i=0∑n+1i!Fn(i)(1)(x0−1)i
而递推式转化为
F n ( k ) ( 1 ) = k ( k − 1 ) F n − 1 ( k − 1 ) ( 1 ) + 2 k F n − 1 ( k ) ( 1 ) F_n^{(k)}(1)=k(k-1)F_{n-1}^{(k-1)}(1)+2kF_{n-1}^{(k)}(1) Fn(k)(1)=k(k−1)Fn−1(k−1)(1)+2kFn−1(k)(1)
接下来的任务就是考虑上述递推式。
首先考虑边界条件,有 F 0 ( 1 ) = F 0 ′ ( 1 ) = 1 F_0(1)=F_0'(1)=1 F0(1)=F0′(1)=1。这时不难发现,如果令 a i , j a_{i,j} ai,j 表示 F i ( j ) ( 1 ) F_{i}^{(j)}(1) Fi(j)(1),将 { a } ( i , j ) = ( 1 , 1 ) ( n , n + 1 ) \{a\}_{(i,j)=(1,1)}^{(n,n+1)} {a}(i,j)=(1,1)(n,n+1) 排列成一个二维矩阵,那么 a i , j a_{i,j} ai,j 仅可以从 a i − 1 , j a_{i-1,j} ai−1,j(向下传递)和 a i − 1 , j − 1 a_{i-1,j-1} ai−1,j−1(右下传递)处转移。那么这时考虑 F n ( k ) ( 1 ) F_{n}^{(k)}(1) Fn(k)(1) 项,如果要从 F 0 ( 1 ) F_{0}(1) F0(1) 和 F 0 ′ ( 1 ) F_{0}'(1) F0′(1) 开始计算贡献,那么必然是 F 0 ′ ( 1 ) F_0'(1) F0′(1) 进行了 k k k 次右下传递,然后再进行了 n − k + 1 n-k+1 n−k+1 次向下传递得到的。注意 F 0 ( 1 ) F_0(1) F0(1) 只要经过向下传递就会乘以 k = 0 k=0 k=0 而直接消失,因而它不会产生贡献。
再次观察递推式,不难发现如果进行了一次右下传递(即从 F n − 1 ( k − 1 ) ( 1 ) F_{n-1}^{(k-1)}(1) Fn−1(k−1)(1) 处转移)时,一定会乘以 k ( k − 1 ) k(k-1) k(k−1)。因而对于得到的 F n ( k ) ( 1 ) F_{n}^{(k)}(1) Fn(k)(1),考虑它的任意一条转移路径,则它必然乘有系数 k ! ( k − 1 ) ! k!(k-1)! k!(k−1)!。
还是只考虑其中一条从 F 0 ′ ( 1 ) F_0'(1) F0′(1) 开始的转移路径。接下来考虑向下传递过程中的系数变化。由于向下传递可以在任意列(即任意阶导数)处发生,因而它的系数乘以的 2 k 2k 2k 是随着导数阶数变化而变化的,但是也仅关于此变化。因而可以考虑 F n k ( 1 ) F_{n}^{k}(1) Fnk(1) 在经过的 n − k + 1 n-k+1 n−k+1 次向下转移过程中到底在哪些列(导数阶数)处进行过转移。这个就是经典的生成函数问题:
[ x n − k + 1 ] ∏ j = 1 k ( ∑ i = 0 + ∞ ( 2 j x ) i ) [x^{n-k+1}]\prod_{j=1}^{k}\left(\sum_{i=0}^{+\infty}(2jx)^i\right) [xn−k+1]j=1∏k(i=0∑+∞(2jx)i)
即, ∑ i = 0 + ∞ ( j x ) i \displaystyle \sum_{i=0}^{+\infty}(jx)^i i=0∑+∞(jx)i 表示 F n k ( 1 ) F_{n}^{k}(1) Fnk(1) 在第 j j j 列进行的向下转移状态, x i x^i xi( i ∈ [ 0 , + ∞ ] i \in [0,+\infty] i∈[0,+∞])项系数表示在这里向下转移了 i i i 次的方案对 F n k ( 1 ) F_{n}^{k}(1) Fnk(1) 的贡献。这里不是指数生成函数是因为如果在第 j j j 列向下转移次数确定了,则方案是唯一确定的,而这个方案对系数的贡献是只与列数和转移次数有关,为 ( 2 j ) i (2j)^i (2j)i。
不难注意到当 x x x 充分小的时候,利用泰勒展开有 ∑ i = 0 + ∞ ( 2 j x ) i = 1 1 − 2 j x \displaystyle \sum_{i=0}^{+\infty}(2jx)^i=\dfrac{1}{1-2jx} i=0∑+∞(2jx)i=1−2jx1。因而原式转化为(带入右下转移的系数贡献):
k ( k − 1 ) ! [ x n − k + 1 ] ∏ j = 1 k 1 1 − 2 j x k(k-1)![x^{n-k+1}]\prod_{j=1}^{k}\dfrac{1}{1-2jx} k(k−1)![xn−k+1]j=1∏k1−2jx1
这时对于一个特定的 k k k,容易发现需要求的系数项也不同。这不利于后续的求和处理。考虑通过同时乘以 x k x^k xk 以统一到 x k x^k xk 项系数:
k ! ( k − 1 ) ! [ x n − k + 1 ] ∏ j = 1 k 1 1 − 2 j x = k ! ( k − 1 ) ! [ x n + 1 ] ∏ j = 1 k x 1 − 2 j x k!(k-1)![x^{n-k+1}]\prod_{j=1}^k \dfrac{1}{1-2jx} = k!(k-1)![x^{n+1}]\prod_{j=1}^k \dfrac{x}{1-2jx} k!(k−1)![xn−k+1]j=1∏k1−2jx1=k!(k−1)![xn+1]j=1∏k1−2jxx
将上式回代回最开始的泰勒展式:
∑ k = 0 n + 1 ( x 0 − 1 ) k k ! ( k ! ( k − 1 ) ! × [ y n + 1 ] ∏ j = 1 k y 1 − 2 j y ) = ∑ k = 0 n + 1 ( k − 1 ) ! ( x 0 − 1 ) k ( [ y n + 1 ] ∏ j = 1 k y ( 1 − 2 j y ) ) = ∑ k = 0 n + 1 ( [ y n + 1 ] ∏ j = 1 k ( x 0 − 1 ) ( j − 1 ) y ( 1 − 2 j y ) ) \begin{aligned} &\sum_{k=0}^{n+1}\dfrac{(x_0-1)^{k}}{k!}\left(k!(k-1)!\times [y^{n+1}]\prod_{j=1}^k \dfrac{y}{1-2jy}\right)\\ =&\sum_{k=0}^{n+1}(k-1)!(x_0-1)^k\left([y^{n+1}]\prod_{j=1}^k \dfrac{y}{(1-2jy)}\right)\\ =&\sum_{k=0}^{n+1}\left([y^{n+1}]\prod_{j=1}^k \dfrac{(x_0-1)(j-1)y}{(1-2jy)}\right)\\ \end{aligned} ==k=0∑n+1k!(x0−1)k(k!(k−1)!×[yn+1]j=1∏k1−2jyy)k=0∑n+1(k−1)!(x0−1)k([yn+1]j=1∏k(1−2jy)y)k=0∑n+1([yn+1]j=1∏k(1−2jy)(x0−1)(j−1)y)
上式中将 ( x 0 − 1 ) k (x_0-1)^k (x0−1)k 乘入后面的 k k k 项乘法, ( k − 1 ) ! (k-1)! (k−1)! 也可类似操作。注意这里当 j = 1 j=1 j=1 时 j − 1 = 0 j-1=0 j−1=0 只是形式上的统一。在后续计算中这里会当作 1 1 1 处理。
考虑上式如何快速计算。首先取系数运算和求和运算的运算顺序可以互换。不难发现上式最麻烦的地方在于对于不同的 k k k,乘除的式子都不尽相同,而且随着 k k k 变化都需要保留 n + 1 n+1 n+1 项。但是递归树 NTT 可以求解下列式子:
h ( 1 , n ) = ∑ i = 1 n ( ∏ j = 1 i f j ( x ) ) ( ∏ j = i + 1 n g j ( x ) ) h(1,n)=\sum_{i=1}^n \left(\prod_{j=1}^if_j(x)\right)\left(\prod_{j=i+1}^ng_j(x)\right) h(1,n)=i=1∑n(j=1∏ifj(x))(j=i+1∏ngj(x))
其中 f f f 和 g g g 的次数和不超过 NTT 计算范围。考虑维护 h ( l , r ) h(l,r) h(l,r) 的求和答案,通过分治计算出 h ( l , m ) h(l,m) h(l,m) 和 h ( m + 1 , r ) h(m+1,r) h(m+1,r),然后考虑合并答案: h ( l , r ) = h ( l , m ) ∏ j = m + 1 r g j ( x ) + h ( m + 1 , r ) ∏ j = l m f j ( x ) \displaystyle h(l,r)=h(l,m)\prod_{j=m+1}^rg_j(x)+h(m+1,r)\prod_{j=l}^mf_j(x) h(l,r)=h(l,m)j=m+1∏rgj(x)+h(m+1,r)j=l∏mfj(x),维护 h h h 和 f , g f,g f,g 的区间乘积即可在 O ( n log 2 n ) \mathcal O(n \log^2 n) O(nlog2n) 内完成计算。
因而考虑原式如何转化到这一方法进行计算。不难注意到,可以提出分母的 ∏ j = 1 n + 1 ( 1 − 2 j y ) \displaystyle \prod_{j=1}^{n+1} (1-2jy) j=1∏n+1(1−2jy),则原式等于:
[ y n + 1 ] ∑ k = 0 n + 1 ( ∏ j = k + 1 n + 1 ( 1 − 2 j y ) ) ( ∏ j = 1 k ( x 0 − 1 ) ( j − 1 ) y ) ( ∏ j = 1 n + 1 ( 1 − 2 j y ) ) [y^{n+1}]\sum_{k=0}^{n+1}\dfrac{\left(\prod_{j=k+1}^{n+1} (1-2jy)\right)\left(\prod_{j=1}^k (x_0-1)(j-1)y\right)}{\left(\prod_{j=1}^{n+1} (1-2jy)\right)} [yn+1]k=0∑n+1(∏j=1n+1(1−2jy))(∏j=k+1n+1(1−2jy))(∏j=1k(x0−1)(j−1)y)
因而 f j ( x ) = ( x 0 − 1 ) ( j − 1 ) y f_j(x)=(x_0-1)(j-1)y fj(x)=(x0−1)(j−1)y,而 g j ( x ) = 1 − 2 j x g_j(x)=1-2jx gj(x)=1−2jx,最后计算下面的乘积,同样使用分治的方法进行计算。这里 f 1 ( x ) f_1(x) f1(x) 注意 j − 1 j-1 j−1 不是 0 0 0。最后进行多项式求逆就可以使用上式的方法进行计算。总复杂度 O ( n log 2 n ) \mathcal O(n \log^2n) O(nlog2n)。
// U表示f多项式,F表示g多项式,G表示乘积和多项式。add、mul都是多项式上加法和乘法运算
void sol( int rt , int l , int r ) {if( l == r ) {U[rt] = { 0 , (int) ( 1ll * ( x0 + P - 1 ) % P * ( l == 1 ? 1 : l - 1 ) % P ) };F[rt] = { 1 , (int) ( P - 2ll * l % P ) };G[rt] = { 0 , (int) ( 1ll * ( x0 + P - 1 ) % P * ( l == 1 ? 1 : l - 1 ) % P ) };return;}int m = l + r >> 1;sol( rt << 1 , l , m );sol( rt << 1 | 1 , m + 1 , r );vi ul = U[rt << 1] , fr = F[rt << 1 | 1];F[rt] = mul( F[rt << 1] , F[rt << 1 | 1] );U[rt] = mul( U[rt << 1] , U[rt << 1 | 1] );G[rt] = add( mul( G[rt << 1 | 1] , ul ) , mul( G[rt << 1] , fr ) );
}void solve() {cin >> n >> x0;if( !n ) {cout << x0 << endl;return;}pw[0]=1;for(int i=1;i<=n+1;i++)pw[i]=pw[i-1]*1ll*(x0+P-1)%P;fac[0] = 1 , p2[0] = 1;rep( i , 1 , n + 1 ) fac[i] = fac[i - 1] * 1ll * i % P , p2[i] = p2[i - 1] * 2 % P;ifac[n + 1] = Pow( fac[n + 1] , P - 2 );per( i , n + 1 , 1 ) ifac[i - 1] = ifac[i] * 1ll * i % P;sol( 1 , 1 , n + 1 );vi re = F[1];rep( i , 0 , n + 1 ) H[i] = re[i];Inv( H , A , n + 2 );vi ta( n + 2 ) , tg = G[1];rep( i , 0 , n + 1 ) ta[i] = A[i];vi ret = mul( ta , tg );printf("%d\n",ret[n + 1]);
}
法二:考虑使用指数生成函数,具体原因见下方分析。
H ( z , x ) = ∑ i = 0 + ∞ F i ( x ) i ! z i H(z,x)=\sum_{i=0}^{+\infty}\dfrac{F_i(x)}{i!}z^i H(z,x)=i=0∑+∞i!Fi(x)zi
不难发现:
KaTeX parse error: Undefined control sequence: \part at position 9: \dfrac{\̲p̲a̲r̲t̲ ̲H(z,x)}{\part z…
而上式对 x x x 求导有:
KaTeX parse error: Undefined control sequence: \part at position 9: \dfrac{\̲p̲a̲r̲t̲ ̲H(z,x)}{\part x…
注意到刚好求导后发生了系数上的移位,考虑带入 F i + 1 ( x ) = ( x 2 − 1 ) F i ′ ( x ) F_{i+1}(x)=(x^2-1)F'_{i}(x) Fi+1(x)=(x2−1)Fi′(x) 以消除移位,有:
KaTeX parse error: Undefined control sequence: \part at position 32: … (x^2-1)\dfrac{\̲p̲a̲r̲t̲ ̲H(z,x)}{\part x…
这时就体现出这里为什么需要指数生成函数了——移项的时候发生的系数错位刚好可以通过求导产生的系数和阶乘抵消。如果使用普通生成函数则此时会多一项 i i i 的系数无法解决。
因而得到
KaTeX parse error: Undefined control sequence: \part at position 9: \dfrac{\̲p̲a̲r̲t̲ ̲H(z,x)}{\part z…
考虑使用特征线法,即令 x , y , H x,y,H x,y,H 都是关于 t t t 的函数。则特征方程为
d z d t = 1 , d x d t = 1 − x 2 , d H d t = 0 \dfrac{{\rm d}z}{{\rm d}t}=1, \dfrac{{\rm d}x}{{\rm d}t}=1-x^2, \dfrac{{\rm d}H}{{\rm d}t}=0 dtdz=1,dtdx=1−x2,dtdH=0
由上式 x , z x,z x,z 关于 t t t 的全微分可得 d z d x = 1 1 − x 2 \dfrac{{\rm d}z}{{\rm d}x}=\dfrac{1}{1-x^2} dxdz=1−x21,可得 e 2 z 1 − x 1 + x = C e^{2z}\dfrac{1-x}{1+x}=C e2z1+x1−x=C。而由于此时 d H d t = 0 \dfrac{{\rm d}H}{{\rm d}t}=0 dtdH=0,因而最终形式一定为 F ( G ( z , x ) ) F(G(z, x)) F(G(z,x)),即 H ( z , x ) = F ( e 2 z 1 − x 1 + x ) H(z,x)=F\left(e^{2z}\dfrac{1-x}{1+x}\right) H(z,x)=F(e2z1+x1−x)。带入边界条件 H ( 0 , x ) = x H(0,x)=x H(0,x)=x 得 H ( z , x ) = ( 1 + x ) − ( 1 − x ) e 2 z ( 1 + x ) + ( 1 − x ) e 2 z H(z,x)=\dfrac{(1+x)-(1-x)e^{2z}}{ (1+x)+(1-x)e^{2z}} H(z,x)=(1+x)+(1−x)e2z(1+x)−(1−x)e2z。
这是一个二元生成函数,最后考虑恢复 z = n z=n z=n 时 F n ( x ) F_n(x) Fn(x),由于仅求一项,因而可以带入 x = x 0 x=x_0 x=x0,则原式变成一个仅关于 z z z 的形式幂级数,因而多项式求逆即可。复杂度 O ( n log n ) \mathcal O(n \log n) O(nlogn)。
J Pumping
题意:给定一个有向图 G ( n , m ) G(n,m) G(n,m),边上有字符,定义一条从 1 1 1 号节点出发到给定终止节点集合结束的路径是好的。现在要求找到一条路径,其边上字符按顺序可以记作 x y z xyz xyz,且满足 x y i z xy^iz xyiz 也是好的, i ∈ [ 0 , + ∞ ] i \in [0,+\infty] i∈[0,+∞]。其中 y i y^i yi 表示 y y y 的 i i i 次拼接。构造一个这样的 x y z xyz xyz。 1 ≤ n ≤ 5 × 1 0 5 1 \le n \le 5\times 10^5 1≤n≤5×105, 0 ≤ m ≤ 1 0 6 0 \le m \le 10^6 0≤m≤106,终止集合大小 k ∈ [ 1 , n ] k \in [1,n] k∈[1,n]。
解法:由于要能延申无穷多次,因而必然有环;并且 y y y 部分可以不存在,也就是 x z xz xz 本身也是一条合法路径,因而考虑从起点到终点上必须经过一个点,该点上可以走出一条环路。假设这个环路起点为 i i i,则从 1 → i 1 \to i 1→i 为 x x x 串,过 i i i 的环为 y y y 串,从 i i i 到任意一个终止集合点的路径为 z z z。
具体而言,首先在反图上 bfs 找出能到终点的点集合,然后在正向图上从 1 1 1 出发,经由可以到达终点的点进行 dfs。如果在 dfs 过程中可以找到一个环即第二次经过某个点 i i i,则 x y xy xy 部分即为 1 → i 1 \to i 1→i 的路径。这时只需要再从 i i i 找到任意一条去终点的路径即可。复杂度 O ( n + m ) \mathcal O(n+m) O(n+m)。
#include <bits/stdc++.h>
#define fp(i, a, b) for (int i = a, i##_ = b; i <= i##_; ++i)
#define fd(i, a, b) for (int i = a, i##_ = b; i >= i##_; --i)using namespace std;
using ll = long long;
const int N = 5e5 + 5;
int n, m, k, ok[N], ed[N], vis[N];
string ans, cur;
vector<pair<int, char>> G[N], H[N];
void dfs(int u) {vis[u] = 1;for (auto [v, c] : G[u]) {if (!ok[v]) continue;if (vis[v] == 1) {if (ans.empty())ans = cur, ans += c, k = v;} else if (!vis[v]) {cur += c;dfs(v);cur.pop_back();}}vis[u] = -1;
}
int dfs2(int u) {vis[u] = 1;if (ed[u]) return 1;for (auto [v, c] : G[u]) {if (!ok[v] || vis[v]) continue;cur += c;if (dfs2(v)) return 1;cur.pop_back();}return 0;
}
void Solve() {scanf("%d%d%d", &n, &m, &k);queue<int> q;for (int x; k--;) scanf("%d", &x), q.push(x), ed[x] = ok[x] = 1;for (int u, v, c; m--;) {scanf("%d%d %c", &u, &v, &c);G[u].push_back({v, c});H[v].push_back({u, c});}while (!q.empty()) {int u = q.front(); q.pop();for (auto [v, c] : H[u])if (!ok[v]) q.push(v), ok[v] = 1;}if (!ok[1]) return puts("-1"), void();dfs(1);if (ans.empty()) return puts("-1"), void();fill(vis, vis + n + 1, 0);dfs2(k);printf("%s\n", (ans + cur).data());
}
int main() {int t = 1;// scanf("%d", &t);while (t--) Solve();return 0;
}
K First Last
题意: n n n 人参赛 k k k 次,问每次都取得第一名或最后一名的概率,输出浮点数。 1 ≤ n , k ≤ 20 1 \le n, k \le 20 1≤n,k≤20。
解法:输出 ( min ( 2 , n ) n ) k \left(\dfrac{\min(2,n)}{n}\right)^k (nmin(2,n))k。
L Grayscale Confusion
题意:给定 n n n 种颜色 { c } i = 1 n \{c\}_{i=1}^n {c}i=1n,由 RGB 三色定义。现要求构造一个函数映射 f : c → [ 0 , 255 ] f:c \to [0,255] f:c→[0,255],使得任意满足严格偏序关系 c i < c j c_i<c_j ci<cj 的颜色对有 f ( c i ) < f ( c j ) f(c_i) <f(c_j) f(ci)<f(cj),并且 f ( c 1 ) = f ( c 2 ) f(c_1)=f(c_2) f(c1)=f(c2),其中颜色的严格偏序定义为三原色的数值都满足严格小于关系,需要报告无解。 1 ≤ n ≤ 1 0 3 1 \le n \le 10^3 1≤n≤103。
解法:首先 c 1 c_1 c1 和 c 2 c_2 c2 不能有严格偏序关系。如果他们确定没有偏序关系了,这时只需要合并这两个点,对满足严格偏序关系的点对建立边,在这个 DAG 上跑一次拓扑排序进行函数映射即可。复杂度 O ( n 2 ) \mathcal O(n^2) O(n2)。
#include <bits/stdc++.h>
using namespace std;
const int N = 1000;
vector<int> G[N + 5];
int ans[N + 5], deg[N + 5];
struct color
{int r, g, b;bool operator<(const color &x) const{return r < x.r && g < x.g && b < x.b;}
} q[N + 5];
queue<int> que;
int main()
{memset(ans, -1, sizeof(ans));int n;scanf("%d", &n);for (int i = 0; i < n; i++)scanf("%d%d%d", &q[i].r, &q[i].g, &q[i].b);if (q[0] < q[1] || q[1] < q[0]){printf("-1");return 0;}for (int i = 2; i < n; i++){for (int j = 2; j < n; j++)if (q[j] < q[i]){deg[i]++;G[j].push_back(i);}if (q[1] < q[i] || q[0] < q[i]){deg[i]++;G[1].push_back(i);}}for (int j = 2; j < n; j++)if (q[j] < q[0] || q[j] < q[1]){G[j].push_back(1);deg[1]++;}for (int i = 1; i < n; i++)if (!deg[i]){que.push(i);ans[i] = 0;}while (!que.empty()){int tp = que.front();que.pop();for (auto x : G[tp]){deg[x]--;ans[x] = max(ans[x], ans[tp] + 1);if (!deg[x])que.push(x);}}ans[0] = ans[1];for (int i = 0; i < n; i++)if (ans[i] == -1 || ans[i] > 255){printf("-1");return 0;}for (int i = 0; i < n; i++)printf("%d\n", ans[i]);return 0;
}
M Fair Equation
题意:给定一个算式 a + b = c a+b=c a+b=c,问能不能通过在这个等式的任意位置至多插入一个数位 [ 0 , 9 ] [0,9] [0,9] 使得该等式成立。 1 ≤ a , b , c ≤ 1 0 6 1 \le a,b,c \le 10^6 1≤a,b,c≤106。
解法:枚举其中两项,看缺省的那一项能不能由给定项添加一个数字得到。模拟即可。
#include <bits/stdc++.h>
using namespace std;
bool change(int x, int y)
{if (x == y)return true;string a = to_string(x), b = to_string(y);for (auto it = b.begin(); it != b.end(); it++){string c = b;b.erase(it);if (a == b)return true;b = c;}return false;
}
int main()
{int a, b, c;scanf("%d + %d = %d", &a, &b, &c);if (change(a, c - b))printf("Yes\n%d + %d = %d\n", c - b, b, c);else if (change(b, c - a))printf("Yes\n%d + %d = %d\n", a, c - a, c);else if (change(c, a + b))printf("Yes\n%d + %d = %d\n", a, b, a + b);elseprintf("No");return 0;
}
相关文章:

2023 年牛客多校第十场题解
C Multiplication 题意:定义 k k k-shift 数是满足 k x y ‾ y x ‾ k\overline{xy}\overline{yx} kxyyx 的数字。给定 k k k,求最大不超过 n n n 的 k k k-shift 数。 1 ≤ n ≤ 1 0 100 1 \le n \le 10^{100} 1≤n≤10100, 2 ≤…...

韦东山老师 RTOS 入门课程(一)RTOS 介绍,熟悉裸机的汇编逻辑
韦东山老师 RTOS 入门课程 课程链接:韦东山直播公开课:RTOS实战项目之实现多任务系统 第1节:裸机程序框架和缺陷_哔哩哔哩_bilibili RTOS 介绍 裸机:固定顺序执行。 中断:可以一直专心做循环里的事情,直…...
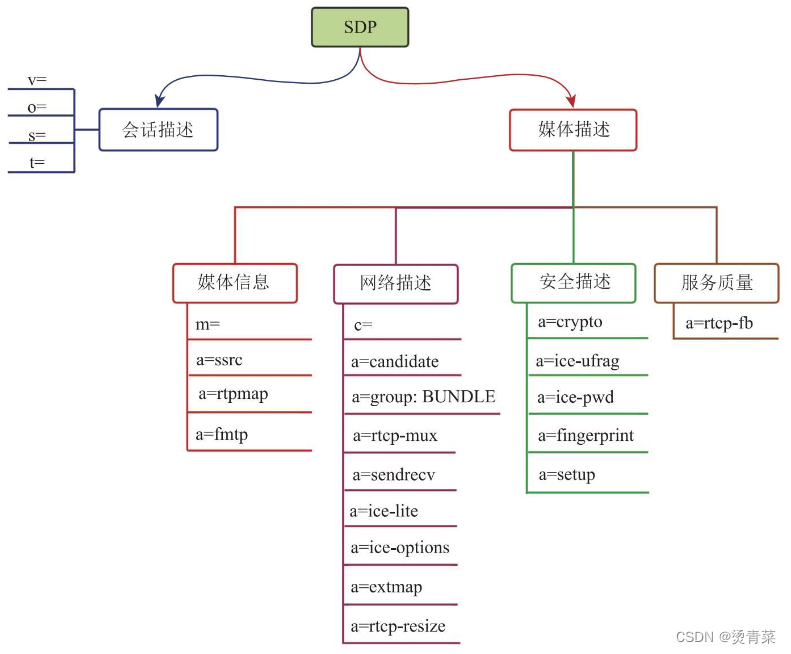
WebRTC | SDP详解
目录 一、SDP标准规范 1. SDP结构 2. SDP内容及type类型 二、WebRTC中的SDP结构 1. 媒体信息描述 (1)SDP中媒体信息格式 i. “artpmap”属性 ii. “afmtp”属性 (2)SSRC与CNAME (3)举个例子 &…...
springboot集成Oauth2.0授权包,5个接口文件配置详解)
Springboot 实践(9)springboot集成Oauth2.0授权包,5个接口文件配置详解
前文讲解实现了spring boot集成Oauth2.0,实现了授权服务器和资源服务器的搭建,并通过浏览器和postman测试,获取到了授权码,用携带授权码的URL能够争取范文到资源。 本文详细讲解spring boot集成Oauth2.0的几个重要文件接口&#…...
最新AI系统ChatGPT程序源码/支持GPT4/自定义训练知识库/GPT联网/支持ai绘画(Midjourney)+Dall-E2绘画/支持MJ以图生图
一、前言 SparkAi系统是基于国外很火的ChatGPT进行开发的Ai智能问答系统。本期针对源码系统整体测试下来非常完美,可以说SparkAi是目前国内一款的ChatGPT对接OpenAI软件系统。 那么如何搭建部署AI创作ChatGPT?小编这里写一个详细图文教程吧!…...
【高频面试题】 消息中间件
文章目录 1、RabbitMQ1.1 RabbitMQ-如何保证消息不丢失1.2 RabbitMQ消息的重复消费问题如何解决的1.3 RabbitMQ中死信交换机 ? (RabbitMQ延迟队列有了解过嘛)1.4 RabbitMQ如果有100万消息堆积在MQ , 如何解决(消息堆积怎么解决)1.5 RabbitMQ的高可用机制有了解过嘛 2、Kafka2.…...
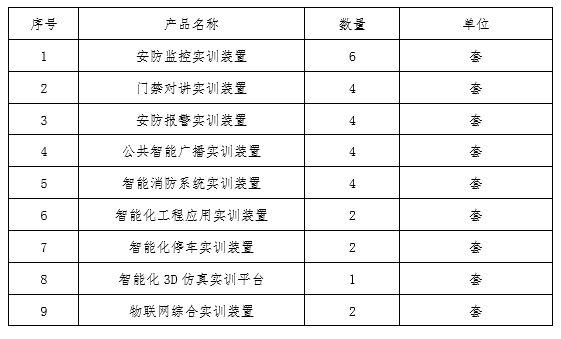
物联网智慧安防实训综合实训基地建设方案
一、系统概述 物联网智慧安防实训综合实训基地是一个为学生提供综合实践、培养技能的场所,专注于物联网技术与智慧安防应用的培训和实训。通过物联网智慧安防实训综合实训基地的建设和运营,学生可以在真实的环境中进行实践训练,提高其物联网技…...

openGauss学习笔记-44 openGauss 高级数据管理-存储过程
文章目录 openGauss学习笔记-44 openGauss 高级数据管理-存储过程44.1 语法格式44.2 参数说明44.3 示例 openGauss学习笔记-44 openGauss 高级数据管理-存储过程 存储过程是能够完成特定功能的SQL语句集。用户可以进行反复调用,从而减少SQL语句的重复编写数量&…...

【Linux】进程信号篇Ⅲ:可重入函数、volatile关键字、SIGCHLD信号
信号Ⅲ 🔗 接上篇七、可重入函数八、volatile 关键字九、SIGCHLD 信号 🔗 接上篇 👉🔗进程信号篇Ⅰ:信号的产生(signal、kill、raise、abort、alarm)、信号的保存(core dump&#x…...

排序算法:冒泡排序
冒泡排序是入门级的算法,但也有一些有趣的玩法。通常来说,冒泡排序有三种写法: 一边比较一边向后两两交换,将最大值 / 最小值冒泡到最后一位;经过优化的写法:使用一个变量记录当前轮次的比较是否发生过交换…...
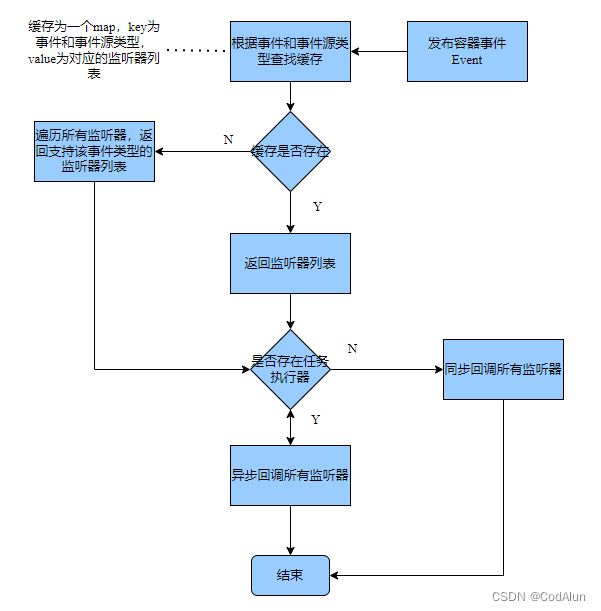
Spring事件监听源码解析
spring事件监听机制离不开容器IOC特性提供的支持,比如容器会自动创建事件发布器,自动识别用户注册的监听器并进行管理,在特定的事件发布后会找到对应的事件监听器并对其监听方法进行回调。Spring帮助用户屏蔽了关于事件监听机制背后的很多细节…...
Cpp学习——list的模拟实现
目录 一,实现list所需要包含的三个类 二,三个类的实现 1.list_node 2.list类 3.iterator_list类 三,功能实现 1.list类里的push_back() 2.iterator类里的运算符重载 3,list类里面的功能函数 1.insert(ÿ…...
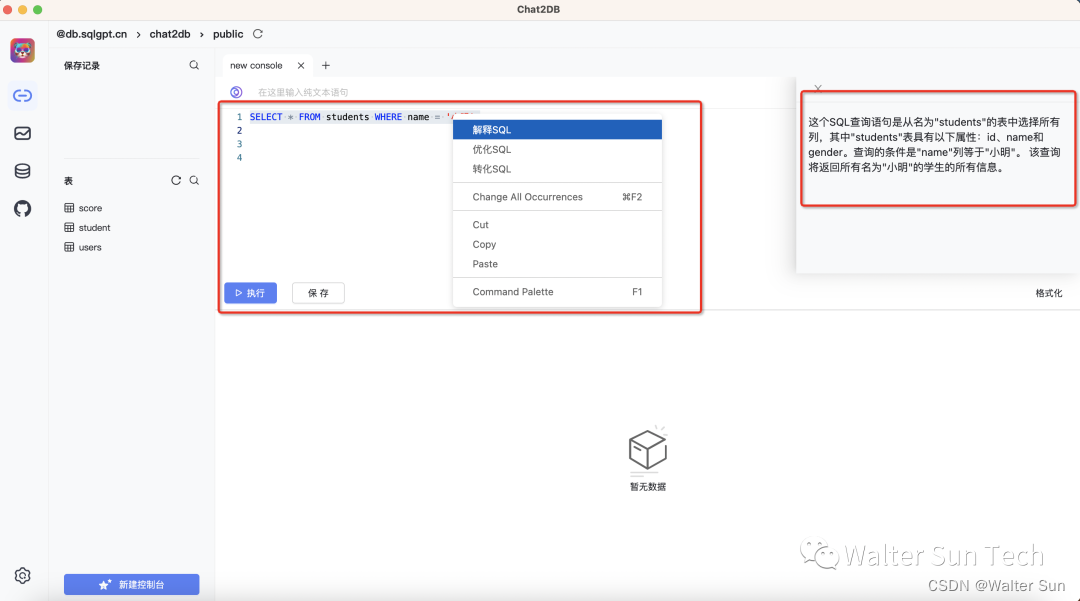
工具推荐:Chat2DB一款开源免费的多数据库客户端工具
文章首发地址 Chat2DB是一款开源免费的多数据库客户端工具,适用于Windows和Mac操作系统,可在本地安装使用,也可以部署到服务器端并通过Web页面进行访问。 相较于传统的数据库客户端软件如Navicat、DBeaver,Chat2DB具备了与AIGC…...
C语言刷题指南(二)
📙作者简介: 清水加冰,目前大二在读,正在学习C/C、Python、操作系统、数据库等。 📘相关专栏:C语言初阶、C语言进阶、C语言刷题训练营、数据结构刷题训练营、有感兴趣的可以看一看。 欢迎点赞 👍…...
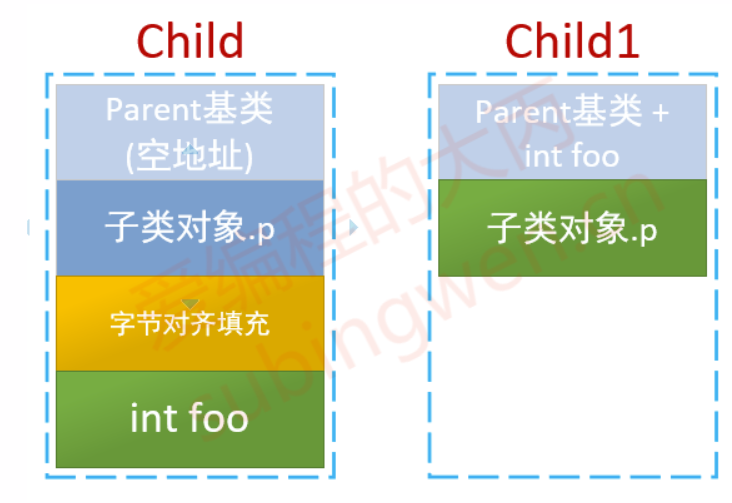
[C++11]
文章目录 1. 自动类型推导1.1 auto1.1.1 推导规则1.1.2 auto的限制1.1.3 auto的应用1.1.4 范围for 1.2 decltype1.2.1 推导规则1.2.2 decltype的应用 1.3 返回类型后置 2.可调用对象包装器、绑定器2.1 可调用对象包装器2.1.1 基本用法2.1.2 作为回调函数使用 2.2 绑定器 3. usi…...
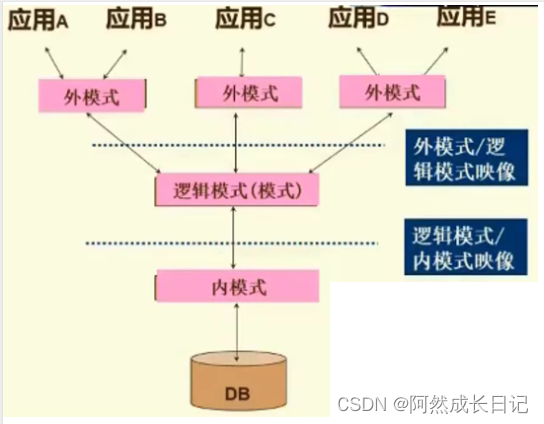
【MySQL系列】--初识数据库
💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤 📃个人主页 :阿然成长日记 …...

Unity导入google.protobuf失败,无法找到google命名空间
问题: 1.刚开始把protobuf的文件夹直接从其他项目里(unity2021)里复制到unity(2020)版本,当时报错protobuf.dll的依赖项system.memory版本不对。 2.没有使用原来的protobuf文件了。使用vs2019的NuGet管理包来下载Google.Protobuf ,仍然报错找…...
使用IDM下载视频出现“由于法律原因,IDM无法下载...
一、问题描述 由于法律原因,IDM无法下载..,如图: 二、原因分析 下载该IDM抓取的M3U8文件,查看其中的内容发现 : #EXT-X-KEY 字段已经写明了加密方式是AES-128,包含一个URI和IV值 #EXTM3U #EXT-X-VERSION:3 #EXT-X-TARGETDURATION:8 #EXT-X-MEDIA-SEQUENCE:0 #EXT-X-KEY:…...
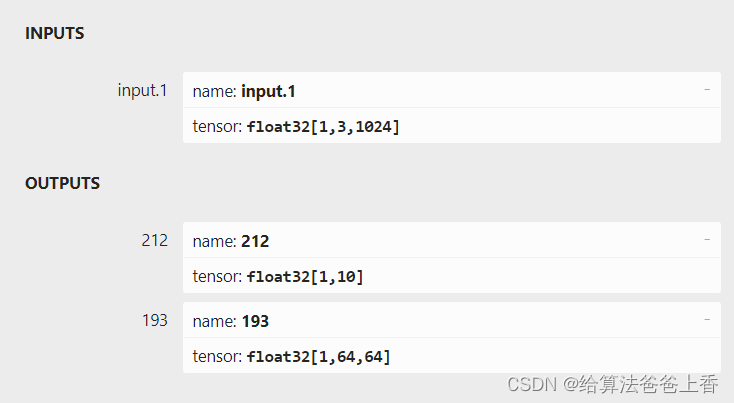
pointnet C++推理部署--tensorrt框架
classification 如上图所示,由于直接export出的onnx文件有两个输出节点,不方便处理,所以编写脚本删除不需要的输出节点193: import onnxonnx_model onnx.load("cls.onnx") graph onnx_model.graphinputs graph.inpu…...

34.Netty源码之Netty如何处理网络请求
highlight: arduino-light 通过前面两节源码课程的学习,我们知道 Netty 在服务端启动时会为创建 NioServerSocketChannel,当客户端新连接接入时又会创建 NioSocketChannel,不管是服务端还是客户端 Channel,在创建时都会初始化自己…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...
