Lookup Singularity
1. 引言
Lookup Singularity概念 由Barry WhiteHat在2022年11月在zkResearch论坛 Lookup Singularity中首次提出:
- 其主要目的是:让SNARK前端生成仅需做lookup的电路。
- Barry预测这样有很多好处,特别是对于可审计性 以及 形式化验证:
- 更易于审计单个lookup argument和各种lookup tables,不再需要数千行的硬编码电路。
- 承认现有的lookup argument方案具有性能瓶颈 但 预测将得到改进:
- 强调可能需要支持巨大table,如size为 2 128 2^{128} 2128的table。
- Lasso/Jolt可能可实现该愿景?
多年来,ZKP的核心元素为check:
- A ∗ B + D = = C A*B+D==C A∗B+D==C
在构建整个电路过程中,重复运用该check。将这种表示的电路称为R1CS。
但是,对于某些任务,R1CS昂贵得令人望而却步,为此,引入了lookup arguments的大量使用。当前,很多ZKP使用lookup argument + R1CS变种多项式承诺 来构建电路。
仅使用R1CS来构建电路存在一些障碍。为此,人们创建了一些hand tuned circuits,在这些hand tuned circuits中,同时包含了多项式约束和lookup arguments。这些hand tuned circuits是特定的,并不是很容易扩展。
1.1 多项式约束
多项式约束是复杂的。电路实现人员构建大量多项式方程式,整个电路定义为由多项式方程式组成的系统。
对这个“由多项式方程式组成的系统” 的solution,构成了a valid proof。很难对方程组的结果进行推理。目前的形式化验证工具无法求解素数域中的多项式方程。
1.2 Lookup argument
lookup argument为set membership check。lookup argument:
- 首次用于做高效的big integer arithmetic。
- 目前还用作VM的控制流
- 做某些不是snark-friendly的运算
- 并不是对所有运算都是更高效的
- 每个lookup会引入一定的prover开销
- 目前控制使用lookup argument的次数 的原因在于,其对Prover来说是昂贵的。
2. 为何Lookup arguments很好?
2.1 语言
当前的snark friendly语言对于新程序员来说是难学的。其使用了不同于之前范式的素数域和多项式约束。而仅使用lookup arguments的语言可能会更简单。当前的语言擅长做snarks定向计算,但当用于传统计算时要昂贵很多。
而仅有lookup的语言,将:
- 既擅长做snarks定向计算
- 也擅长做传统计算
2.2 安全审查
审计人员不再需要取对一组多项式方程式求解。lookup arguments推理起来要简单得多。
如:某电路具有一个ANDgate,有2个输入bit 变量,输出为这2个输入的AND运算结果。
多项式方案为:
(x)(x-1) = 0
y(y-1) = 0
x*y = out
return(out)
Lookup方案为:
out = get x,y from AND table
return(out)
其中AND lookup table为:

由此可知,Lookup方案要简单得多。因此,对于仅有lookup的电路,要更容易找出bug。
2.3 形式化验证
形式化验证工具需对一组多项式方程式求解。现有的形式化验证工具不擅长求解素数域中的多项式方程——这样会引入大量额外工作。
而仅使用lookup argument的话,则可使用现有的形式化验证工具,同时可能可探索一些其它方案。
lookup argument限制了电路中任意point的有限变量集合,使得可能的变量集合由 2 254 2^{254} 2254 限制为了 2 2 2或 2 16 2^{16} 216。这样甚至可支持做state space enumeration 来确认 “电路是正确的”。
2.4 信息论对比
为高效将程序描述为电路,需构建一个电路来将“某输入”映射为“正确的输出”。可将“电路”看成是“每个prover time second编码的信息”。这似乎是对比“实现电路的不同方式”的一种好角度。
多项式约束具有有限的degree:
- 因为degree会影响Prover time。
- degree会限制可编码的信息。
如degree为5的多项式可将5个输入值 映射为 5个输出值。除非增加degree,否则无法在该多项式中包含更多的值。
很多情况下,这样是ok的,因为是使用多项式约束的structure来做计算。因此,乘法运算对应为多项式运算 A ∗ B = = C A*B==C A∗B==C,而XOR运算不是,需要编码为keys to values。
Lookup argument可包含更多的信息。之前已限制lookup table size为 2 28 2^{28} 228个元素。但近期研究成果表明,circuit size仅受限于可灵活完成的最大trusted setup——会限制table_size。
Baloo: Nearly Optimal Lookup Arguments中指出:
- 单个多项式约束中可包含约 5 ∗ 2 254 5*2^{254} 5∗2254位信息。
- Lookup argument可包含 2 254 ∗ table_size 2^{254}*\text{table\_size} 2254∗table_size
当使用多项式约束的structure时,多项式约束是很有用的。但随着更大尺寸的table变得可行,这种优势将消失。
3. 结论
若可仅使用lookup argument来高效定义电路,则将由更简单的工具和电路。
这样,lookup argument 将总是比 多项式约束 效率更高。
未来将关注构建以lookup为中心的ZKP工具。
4. 展望
未来工作:
- 比较现有电路的效率
- 构建仅有lookup的语言示例
- 对不同lookup argument效率做对比,并预测改进空间。
- 寻找lookup argument优于(和劣于)多项式约束的实例:
- 寻找lookup argument 和 多项式约束 的worst case。
- 对现有电路进行benchmark,比对效率:
- lookup argument
- lookup + polynomial constraints
参考资料
[1] Lookup Singularity
[2] The lookup singularity - how zero-knowledge proofs can be made simpler and easier to review.
Justin Thaler系列博客
- SNARK Design
- Rollup项目的SNARK景观
- SNARK原理示例
- SNARK性能及安全——Prover篇
- SNARK性能及安全——Verifier篇
- sum-check protocol in zkproof
- sum-check protocol深入研究
- Lasso、Jolt 以及 Lookup Singularity——Part 1
- Lasso、Jolt 以及 Lookup Singularity——Part 2
lookup系列博客
- PLOOKUP
- PLOOKUP代码解析
- Efficient polynomial commitment schemes for multiple points and polynomials学习笔记
- PLONK + PLOOKUP
- PlonKup: Reconciling PlonK with plookup
- PLONK: permutations over lagrange-bases for oecumenical noninteractive arguments of knowledge 学习笔记
- Plonk代码解析
- RapidUp: Multi-Domain Permutation Protocol for Lookup Tables学习笔记
- Lookup argument总览
- Halo2 学习笔记——设计之Proving system之Lookup argument(1)
- 多变量lookup argument
- cq:fast lookup argument
- Lookup Argument性能优化——Caulk
- 2023年 ZK Hack以及ZK Summit 亮点记
- Research Day 2023:Succinct ZKP最新进展
- Lasso、Jolt 以及 Lookup Singularity——Part 1
- Lasso、Jolt 以及 Lookup Singularity——Part 2
相关文章:

Lookup Singularity
1. 引言 Lookup Singularity概念 由Barry WhiteHat在2022年11月在zkResearch论坛 Lookup Singularity中首次提出: 其主要目的是:让SNARK前端生成仅需做lookup的电路。Barry预测这样有很多好处,特别是对于可审计性 以及 形式化验证ÿ…...
idea 本地版本控制 local history
idea 本地版本控制 local history 如何打开 1 自定义快捷键 settings->keymap->搜索框输入 show history -》Add Keyboard Shortcut -》设置为 CtrlAltL 2 右键文件-》local history -》show history 新建文件 版本1,creating class com.geekmice…这个是初…...
【Freertos基础入门】深入浅出freertos互斥量
文章目录 前言一、互斥量是什么?二、互斥量的使用场景三、互斥量的使用1.创建 2.删除互斥量3.give和take四、示例代码总结 前言 FreeRTOS是一款开源的实时操作系统,提供了许多基本的内核对象,其中包括互斥锁(Mutex)。…...
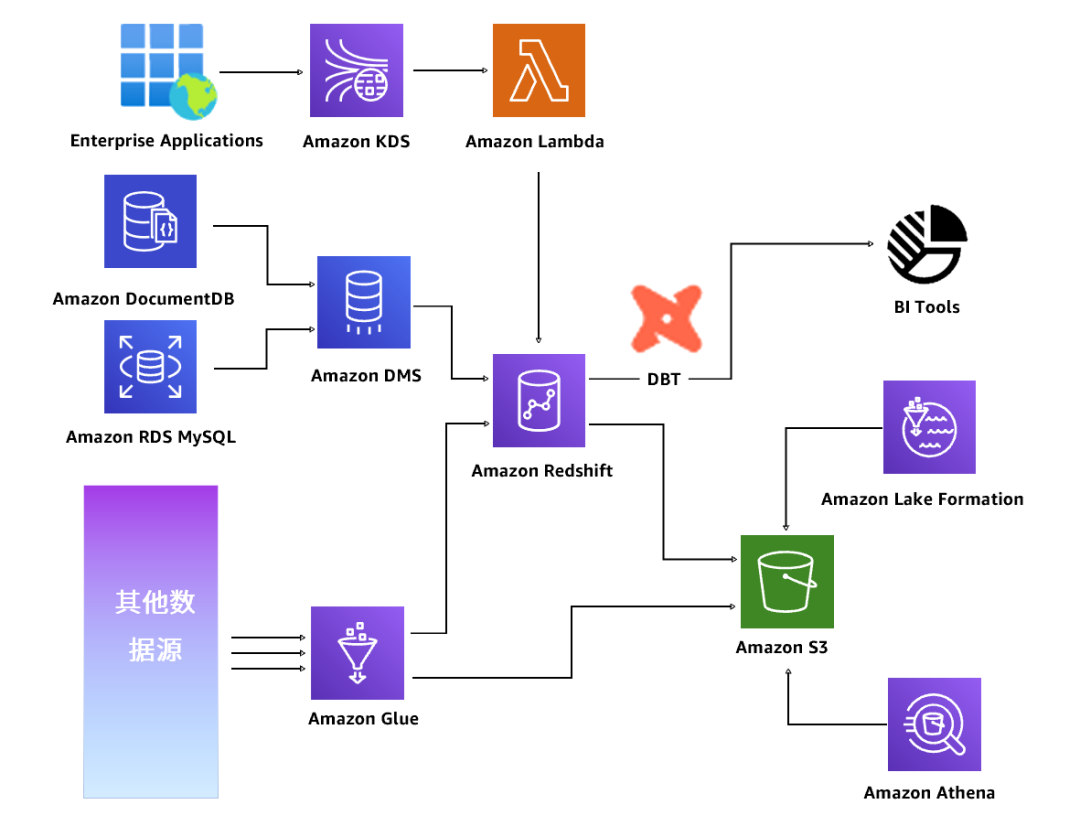
皮爷咖啡基于亚马逊云科技的数据架构,加速数据治理进程
皮爷咖啡(Peet’s Coffee)是美国精品咖啡品牌,于2017年进入中国,为中国消费者带来传统经典咖啡饮品,并特别呈现更加丰富的品质咖啡饮品体验。通过深入应用亚马逊云科技云原生数据库产品Amazon Redshift以及Amazon DMS等…...
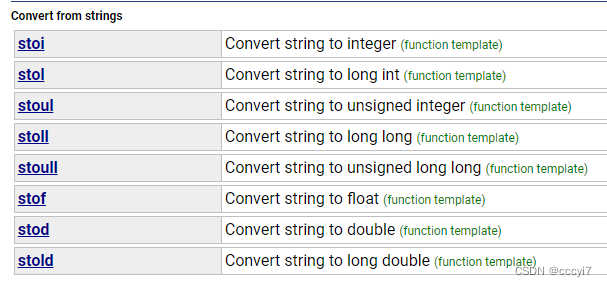
C++ string类详解
⭐️ string string 是表示字符串的字符串类,该类的接口与常规容器的接口基本一致,还有一些额外的操作 string 的常规操作,在使用 string 类时,需要使用 #include <string> 以及 using namespace std;。 ✨ 帮助文档&…...

深入浅出Pytorch函数——torch.nn.init.ones_
分类目录:《深入浅出Pytorch函数》总目录 相关文章: 深入浅出Pytorch函数——torch.nn.init.calculate_gain 深入浅出Pytorch函数——torch.nn.init.uniform_ 深入浅出Pytorch函数——torch.nn.init.normal_ 深入浅出Pytorch函数——torch.nn.init.c…...

一、docker及mysql基本语法
文章目录 一、docker相关命令二、mysql相关命令 一、docker相关命令 (1)拉取镜像:docker pull <镜像ID/image> (2)查看当前docker中的镜像:docker images (3)删除镜像&#x…...
【计算机网络】13、ARP 包:广播自己的 mac 地址和 ip
机器启动时,会向外广播自己的 mac 地址和 ip 地址,这个即称为 arp 协议。范围是未经过路由器的部分,如下图的蓝色部分,范围内的设备都会在本地记录 mac 和 ip 的绑定信息,若有重复则覆盖更新(例如先收到 ma…...
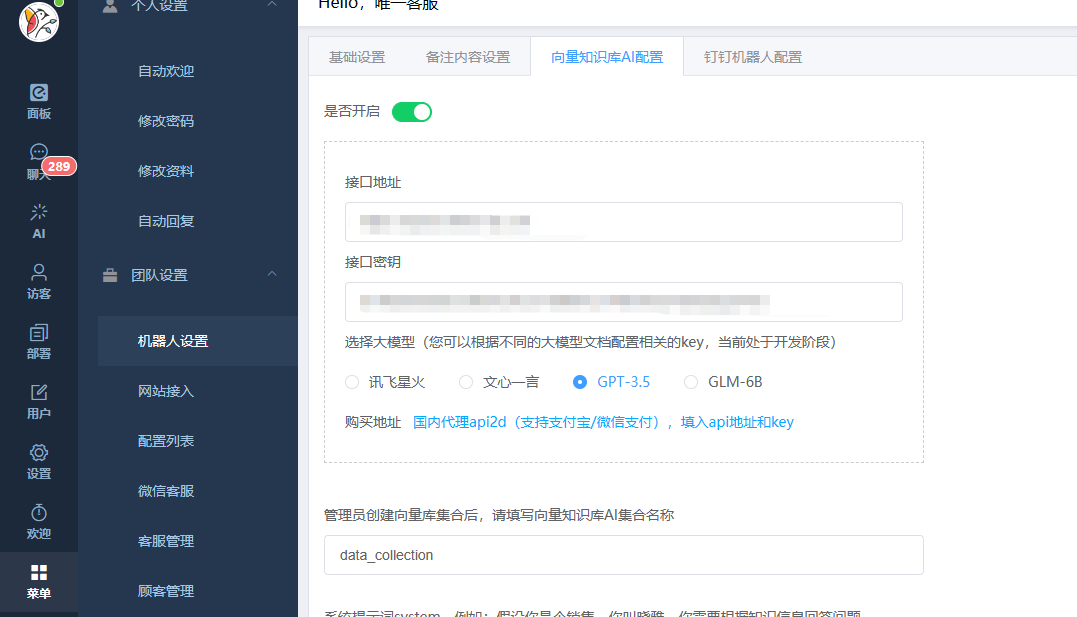
通过微软Azure调用GPT的接口API-兼容平替OpenAI官方的注意事项
众所周知,我们是访问不通OpenAI官方服务的,但是我们可以自己通过代理或者使用第三方代理访问接口 现在新出台的规定禁止使用境外的AI大模型接口对境内客户使用,所以我们需要使用国内的大模型接口 国内的效果真的很差,现在如果想使…...

回归预测 | MATLAB实现BO-SVM贝叶斯优化支持向量机多输入单输出回归预测(多指标,多图)
回归预测 | MATLAB实现BO-SVM贝叶斯优化支持向量机多输入单输出回归预测(多指标,多图) 目录 回归预测 | MATLAB实现BO-SVM贝叶斯优化支持向量机多输入单输出回归预测(多指标,多图)效果一览基本介绍程序设计…...

GAN!生成对抗网络GAN全维度介绍与实战
目录 一、引言1.1 生成对抗网络简介1.2 应用领域概览1.3 GAN的重要性 二、理论基础2.1 生成对抗网络的工作原理2.1.1 生成器生成过程 2.1.2 判别器判别过程 2.1.3 训练过程训练代码示例 2.1.4 平衡与收敛 2.2 数学背景2.2.1 损失函数生成器损失判别器损失 2.2.2 优化方法优化代…...
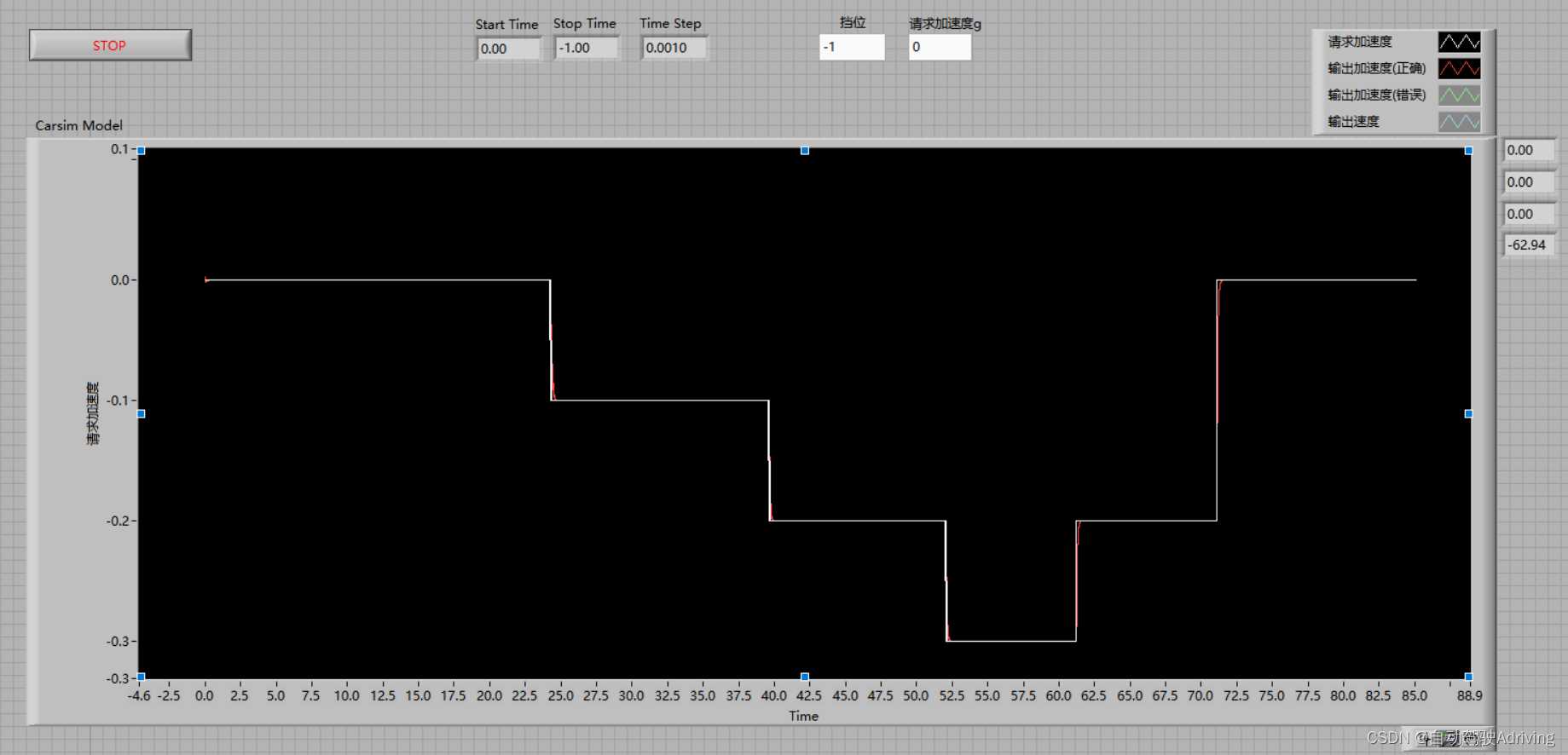
自动驾驶仿真:基于Carsim开发的加速度请求模型
文章目录 前言一、加速度输出变量问题澄清二、配置Carsim动力学模型三、配置Carsim驾驶员模型四、添加VS Command代码五、Run Control联合仿真六、加速度模型效果验证 前言 1、自动驾驶行业中,算法端对于纵向控制的功能预留接口基本都是加速度,我们需要…...
.netcore grpc客户端工厂及依赖注入使用
一、客户端工厂概述 gRPC 与 HttpClientFactory 的集成提供了一种创建 gRPC 客户端的集中方式。可以通过依赖包Grpc.Net.ClientFactory中的AddGrpcClient进行gRPC客户端依赖注入AddGrpcClient函数提供了许多配置项用于处理一些其他事项;例如AOP、重试策略等 二、案…...
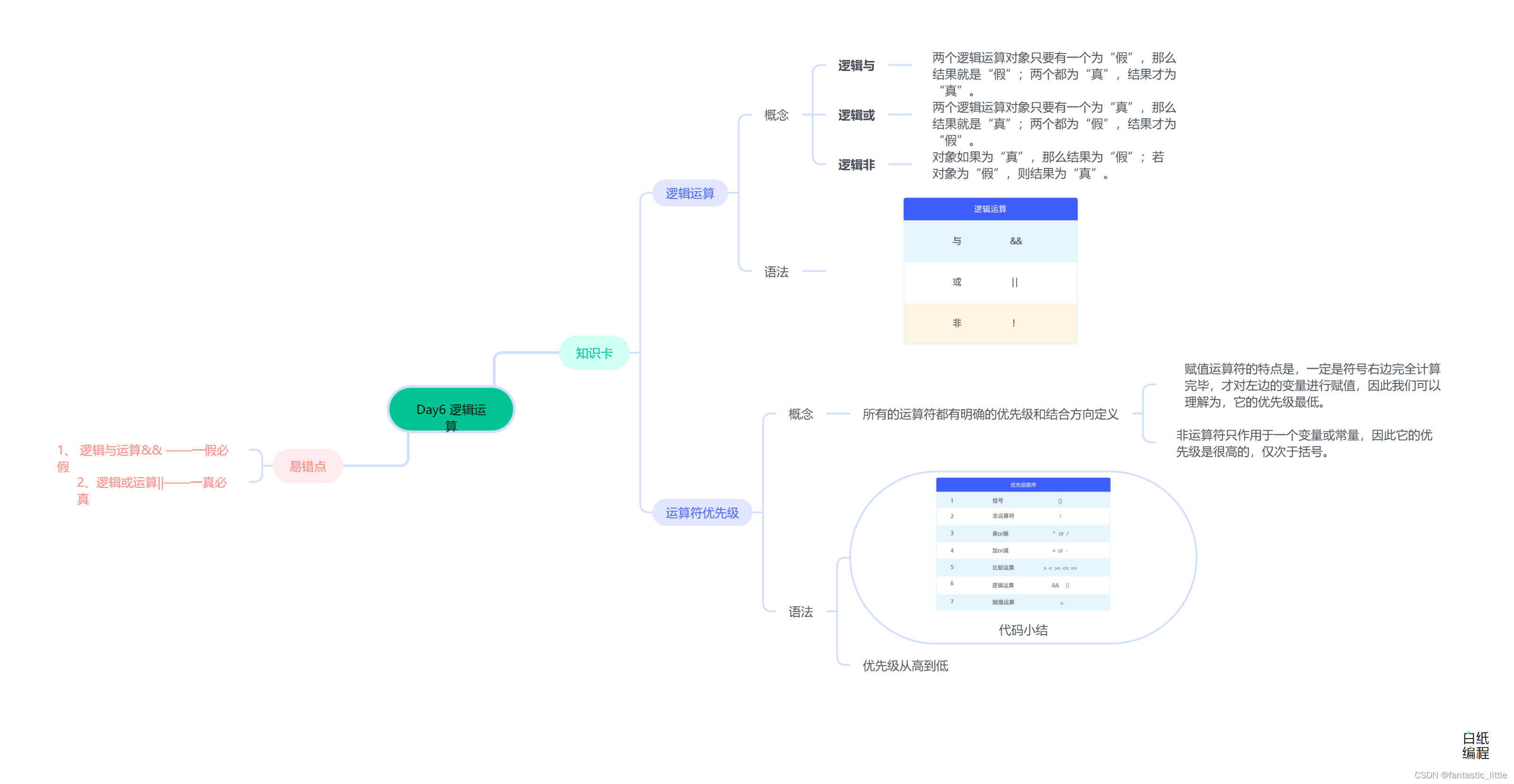
C语言入门_Day7 逻辑运算
目录: 前言 1.逻辑运算 2.优先级 3.易错点 4.思维导图 前言 算术运算用来进行数据的计算和处理;比较运算是用来比较不同的数据,进而来决定下一步怎么做;除此以外还有一种运算叫做逻辑运算,它的应用场景也是用来影…...

什么是Eureka?以及Eureka注册服务的搭建
导包 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/POM/4.0.0 htt…...

Docker安装并配置镜像加速器,镜像、容器的基本操作
目录 1.安装docker服务,配置镜像加速器 (1)安装依赖的软件包 (2)设置yum源,我配置的阿里仓库 (3)选择一个版本安装 (4)启动docker服务,并设置…...

前端 -- 基础 网页、HTML、 WEB标准 扫盲详解
什么是网页 : 网页是构成网站的基本元素,它通常由 图片、链接、文字、声音、视频等元素组成。 通常我们看到的网页 ,常见以 .html 或 .htm 后缀结尾的文件, 因此俗称 HTML 文件 什么是 HTML : HTML 指的是 超文本标记语言,…...

分布式锁实现方式
分布式锁 1 分布式锁介绍 1.1 什么是分布式 一个大型的系统往往被分为几个子系统来做,一个子系统可以部署在一台机器的多个 JVM(java虚拟机) 上,也可以部署在多台机器上。但是每一个系统不是独立的,不是完全独立的。需要相互通信ÿ…...

C语言小练习(一)
🌞 “人生是用来体验的,不是用来绎示完美的,接受迟钝和平庸,允许出错,允许自己偶尔断电,带着遗憾,拼命绽放,这是与自己达成和解的唯一办法。放下焦虑,和不完美的自己和解…...

Flask-flask系统运行后台轮询线程
对于有些flask系统,后台需要启动轮询线程,执行特定的任务,以下是一个简单的例子。 globals/daemon.py import threading from app.executor.ops_service import find_and_run_ops_task_todo_in_redisdef context_run_func(app, func):with …...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...
